“结构”与“配型”的思维指向性

唐德绪

(云南省蒙自一中 661199)

问题1 设数列{an}的前n项和为Sn，满足2Sn=an+1-2n+1+1，n∈N*，且a1，a2+5，a3成等差数列．求数列{an}的通项公式．

思维试验:可令n=1，n=2得关系式联立求a1；

由已知可得n≥2时，2Sn-1=an-2n+1，两式相减．

解(1)当n=1时，

2a1=a2-4+1=a2-3，

①

当n=2时，2(a1+a2)=a3-8+1=a3-7，

②

又a1，a2+5，a3成等差数列，所以a1+a3=2(a2+5).

③

由①②③解得a1=1.

(2)因为2Sn=an+1-2n+1+1，所以当n≥2时，有2Sn-1=an-2n+1.

两式相减得an+1-3an=2n，则可配型为an+1+2n+1=3(an+2n).

又a1+21=3,a2+22=9，所以数列{an+2n}是首项为3，公比为3的等比数列，

所以an+2n=3×3n-1，即an=3n-2n.

问题2 已知数列{an}的前n项和为Sn，满足Sn=2an+(-1)n(n∈N*)．

解当n=1时，a1=S1=2a1-1，得a1=1.

由Sn=2an+(-1)n，当n≥2时，得Sn-1=2an-1+

(-1)n-1.

两式相减得an=2an-1-2(-1)n，n≥2.

……

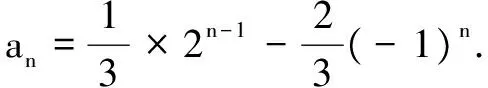
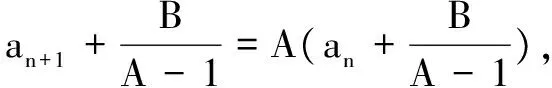
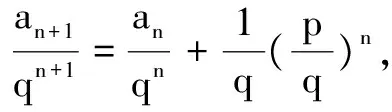
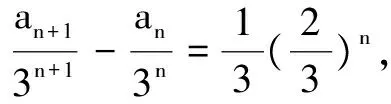
上述(n-2)个式子累加得：

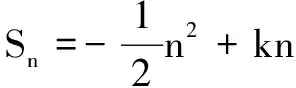
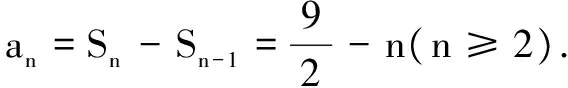
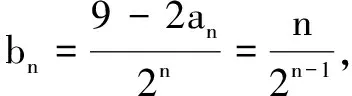
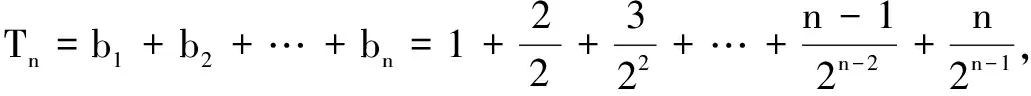
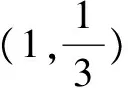
(1)求数列{an}和{bn}的通项公式；

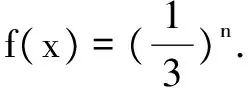
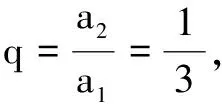
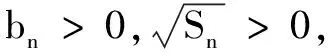
当n≥2时，bn=Sn-Sn-1=n2-(n-1)2=2n-1，

当n=1时，b1=1也适合此通项公式．所以bn=2n-1 (n∈N*)．

参考文献：

[1]G.波利亚.怎样解题——数学教学法的新面貌[M].上海:上海科技教育出版社,2002.