利用公式化通法解题
2018-04-23邢雅峰
邢雅峰
(广东省汕尾市海丰县彭湃中学 516400)
由等差数列{an}与等比数列{bn}的乘积构成的新数列{an·bn}的求和问题,称之为“差比型”数列.求这类数列前n项的和时当然是“错位相减法”,这种固定的求解模式学生易掌握,但对运算化简能力要求较高计算量略大易出错,那么有没有一个通用结论公式,在计算上更快捷、更准确呢?经过一番探索,有了如下公式化结论的发现.
一、公式化结论的证明
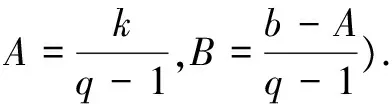
证明由Sn=(k+b)q+(2k+b)q2+(3k+b)q3+…+(kn+b)qn,
①
所以qSn=(k+b)q2+(2k+b)q3+(3k+b)q4+…+(kn+b)qn+1.
②
①-②得: (1-q)Sn=(k+b)q-(kn+b)qn+1+k(q2+q3+q4+…+qn),
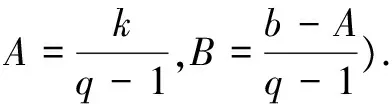
二、牛刀小试
例1 (2017年天津理)已知{an}为等差数列,前n项和为Sn(n∈N*),{bn}是首项为2的等比数列,且公比大于0,b2+b3=12,b3=a4-2a1,S11=11b4.
(1)求{an}和{bn}的通项公式;
(2)求数列{a2nb2n-1}的前n项和(n∈N*).
解析这里着重第二问.(1)an=3n-2,bn=2n.
(2)由(1)可得a2n=6n-2,b2n+1=22n-1,a2nb2n-1=(3n-1)×4n.
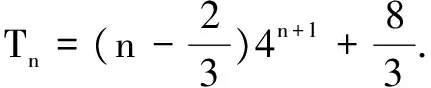
例2 (2017年山东文)已知{an}是各项均为正数的等比数列,且a1+a2=6,a1·a2=a3.
(1)求数列{an}通项公式;
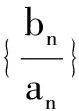
解析(1)可解得an=2n.
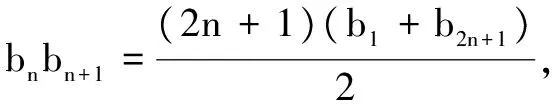

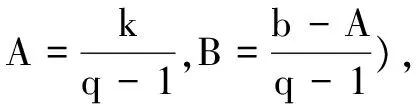


三、高考中书写解题的规范格式(不失分)
例3 (2014年新课标Ⅰ文)已知{an}是递增的等差数列,a2,a4是方程x2-5x+6=0的根.
(1)求{an}的通项公式.
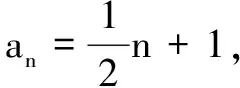
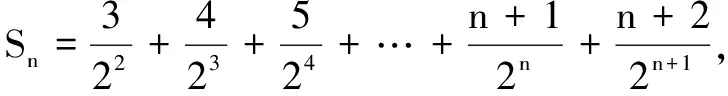

以上是答案,那么高考如何答题才能既保证结果的正确性, 又得到过程分呢?我们只需在这步 (可以省去这步后面繁琐的化简整理),
参考文献:
[1]李秉权. 解密错位相减法[J]. 中学数学研究(广东),2017(8):7-8.
[2]胡炯涛. 高中数学成功之路(特级教师导学丛书)[M].上海:上海交通大学出版社,1996.
