酸化期间基于BP神经网络法的井底压力计算

韩 雄 何 峰 王 超

1. 中国石油川庆钻探工程有限公司钻采工程技术研究院 2.中国石油川庆钻探工程有限公司井下作业公司

酸化是天然气开采储层改造的主要技术手段之一。酸化期间形成的人工裂缝影响着酸化范围，并最终影响储层改造效果，工程上往往利用井底压力数据、井筒参数、地层参数、施工参数等，借助裂缝扩展模型（如KGN模型等）来判断井底裂缝扩展延伸情况，并及时调整施工参数（如排量、段塞大小等）对裂缝特征进行控制。为提高井底裂缝扩展情况判断的准确性，掌握准确的井底压力数据显得至关重要[1-3]。

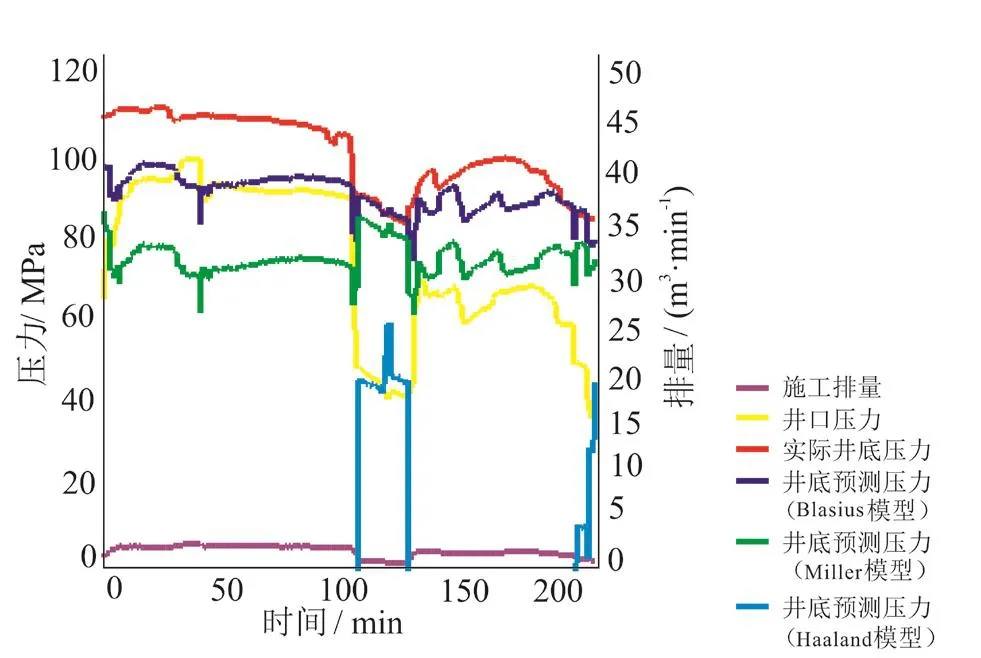
图1 经典模型井底压力计算结果图（GS9井灯四下亚段）

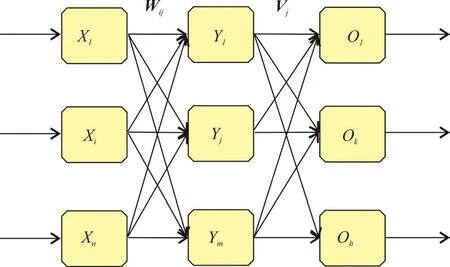
图2 神经网络工作原理图

1 井底压力获取方法简介

酸化期间获取准确井底压力的方式是采用井下压力计进行压力采集，但受井场作业环境、井身结构和地层岩性等因素的制约，目前还无法在酸化期间实时读取井下压力。另一种方式利用经典的井底压力计算模型进行预测（如Miller、Haaland、Blasius模型等），经典模型通常是在基本假设基础上建立起来的理想模型，对于极其复杂的井筒流体流动，则难以准确描述[4-6]，计算结果往往偏差较大，误差基本在20%以上（图1），可用性不高。一种基于神经网络方法的预测技术在处理影响因素复杂且难以用物理定律准确描述的非线性问题时优势突出（如人脸识别、语音识别等），如果把该方法不依赖流体物理方程进行推演的优势应用到酸化期间井底压力计算上，可避开经典模型适应性差的问题，为井底压力计算提供了一条新途径。

2 BP神经网络井底压力预测方法

2.1 BP神经网络简介

BP神经网络的本质是模拟人的神经元工作机理，具备存储和应用经验的自然特性，避开了传统解析方程法对复杂现象难以准确描述的困难，在处理非线性、混沌性问题优势突出[7-8]。BP神经网络包含数据输入层、隐含层、输出层。工作模式为：神经网络训练期间输入数据Xi，并调整隐含层的权值矩阵（Wij∶Vj），直到实际输出数据Ok与预期的输出数据O'k一致，通过大量数据的反复学习便形成了一个描述这类事件输入数据与输出数据规律的BP神经网络（图2）。后期利用训练好的神经，输入初始数据即可得到预测数据[9]。

2.2 BP神经网络井底压力预测模型建立

将BP神经网络方法引入储层改造施工的井底压力预测，对工区内历史作业井的施工数据进行自我学习分析，建立起一套内部反射传递网络，输入实时施工参数，即可预测出井底压力，避开了井筒复杂的流体力学分析计算过程，同时它具有自主学习能力，随着数据库的扩大，预测精度将越来越高。

井底压力计算的关键是井筒摩阻的计算，因此核心是利用神经网络计算出井筒流动摩阻系数λ（单位井筒长度上的摩阻压降），然后可用下列公式简单计算出井底压力：

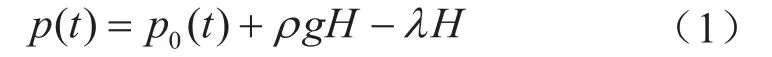
式中p表示预测的井底压力，MPa；p0表示井口压力，MPa；ρ表示液体密度，g/cm3；g表示重力系数，0.009 81 m/s2；λ表示摩阻系数，MPa/m；H表示井筒深度，m。

利用前期历史井施工数据进行神经网络训练，获得井筒流动摩阻系数λ的步骤如下。

1）输入层

输入层数据是驱动对象（即影响摩阻系数的因素）当前状态的特征矩阵[10]。井筒摩阻系数主要与液体性质、流量、管柱结构相关，因此输入层数据选择为：

输入数据Xn= [ 排量 内径 黏度 密度]

如果在一个工区内某个特征量非常接近，则该特征量可以不作为输入值。

2）隐含层

对于井底压力预测的输入数据Xn是多个量，因此第一层权值矩阵为二位向量Wij；而预测井底压力p是单个量，因此第二层权值矩阵为一维向量Vj。

对于权值矩阵Wij、Vj和阀值矩阵aj、b的初始值设置为[0、1]之间的随机数。

激活函数：

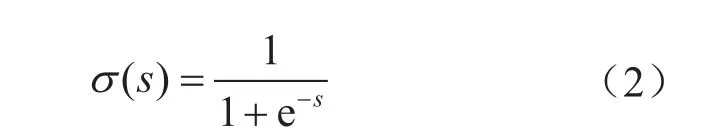
式中σ表示激活函数值，无量纲；s表示激活参数，无量纲。

对于第一层的激活参数s表达式为：

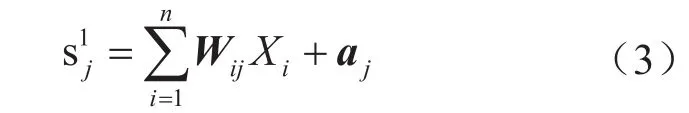
对于第二层的激活参数s表达式为：

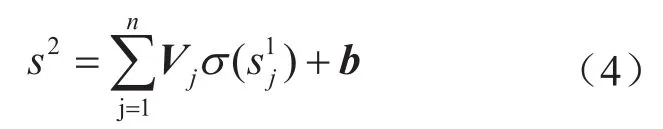
3）数据输出层

训练期间 ：通过预设的 Wij、Vj、aj、b 及激活函数计算出摩阻系数λ，并与实际摩阻系数λ0比较，得到一个误差函数ek，使用最快梯度法反复调整Wij、Vj使误差函数值达到预期要求e0，即可得到最终的权值矩阵Wij、Vj和阀值矩阵aj、b。其中：

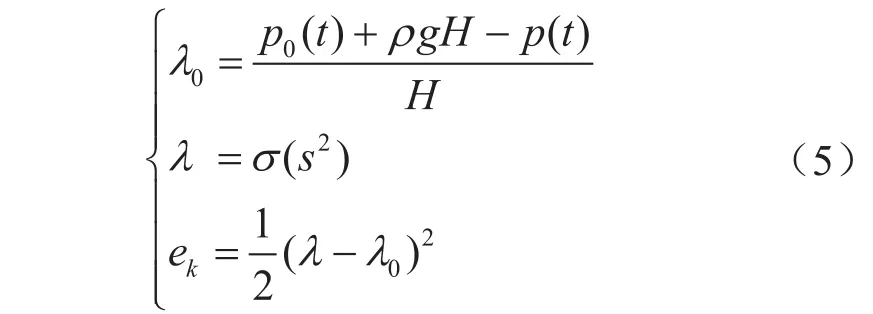
权值调整模式及阀值调整模式：

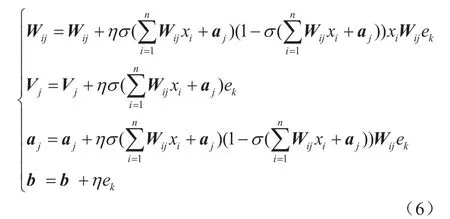
式中η表示学习效率，根据经验取0.1。

3 酸化井BP网络训练及分析

3.1 训练的BP神经网络模型

选取川渝油气田工区内GS8井灯四上及灯四下亚段、GS9井灯四上亚段、GS18井灯四段、GS20井灯四上亚段及灯四下亚段等15井次酸化施工数据（井口压力、井底压力、排量、黏度、内径、深度）作为样本，开展BP神经网络训练，获得摩阻系数神经网络矩阵（表1）。基于建立的摩阻系数神经网络矩阵，结合公式（1），在GS9井灯四下亚段进行酸化期间的井底压力计算，并与实际井底压力对比（实际井底压力采用随酸化管柱下入井底的电子压力计录取），如图3，对比结果表明：BP神经网络法计算的井底压力与实测井底压力具有良好的一致性，最大误差在8.1%以内，同解析模型相比（如blasius模型），无论在趋势上还是预测数值上BP神经网络法均具有更好的准确性。

3.2 输入参数对计算结果影响程度分析

利用建立的神经网络，选取液体密度、黏度、流速及管柱内径等4个影响因素进行三水平的正交模拟计算试验，分析各个因素对计算结果的影响程度（表2）。分析结果如表2所示，可以看出在神经网络预测模型中，各个输入参数影响计算结果的敏感程度依次为：液体流速＞液体黏度＞液体密度＞管柱内径。因此在利用BP神经网络方法计算井底压力时准确掌握液体排量和液体性能参数至关重要。

4 现场应用

利用大量井施工历史数据建立的BP神经网络编制出井底压力计算软件，并在川渝地区灯影组多口井开展井底压力计算试验（施工井井深4 959～5 034 m，排量5.2～6.0 m3/min），计算结果与井底压力计实测数据对比（图4），最大误差7.8%（表3），说明训练的BP神经网络具有较好的适应性。

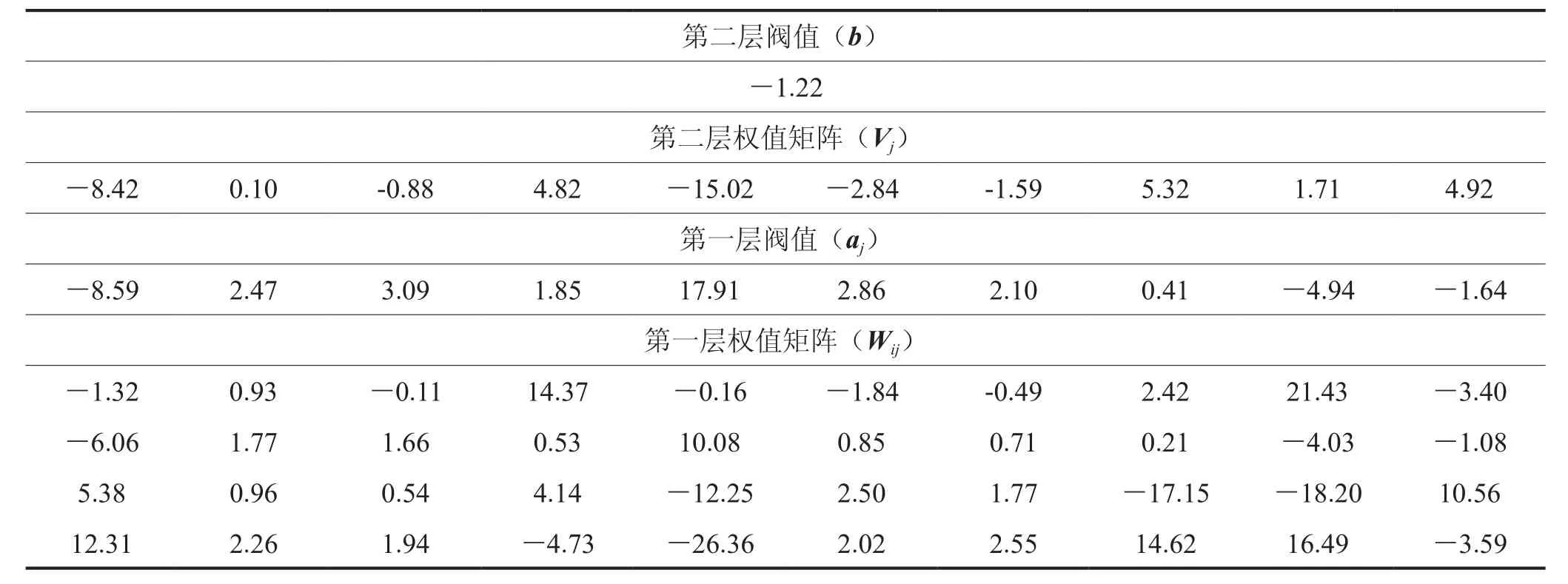
表1 训练好的摩阻系数计算神经网络表

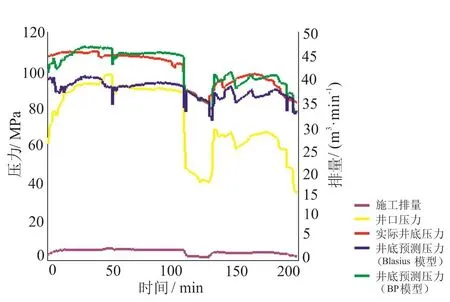
图3 BP神经网络法在GS9灯四下亚段的井底压力预测效果图

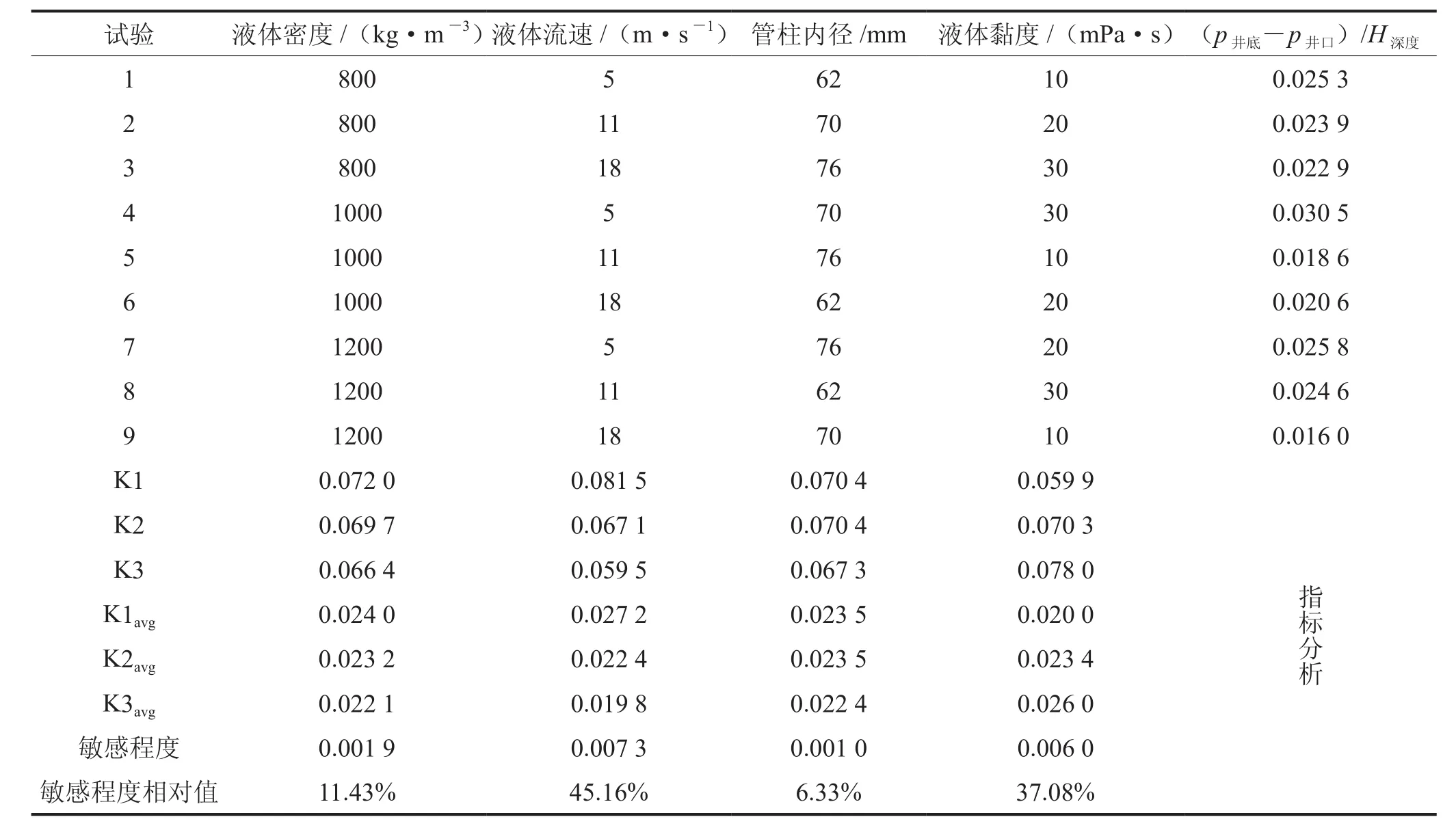
表2 计算结果影响因素分析表

5 应用范围分析

建立BP神经网络的适应性取决于训练期间使用的历史数据所覆盖井况和数据量的多少。本文建立的BP神经网络是选用川渝气田灯影组气藏的气

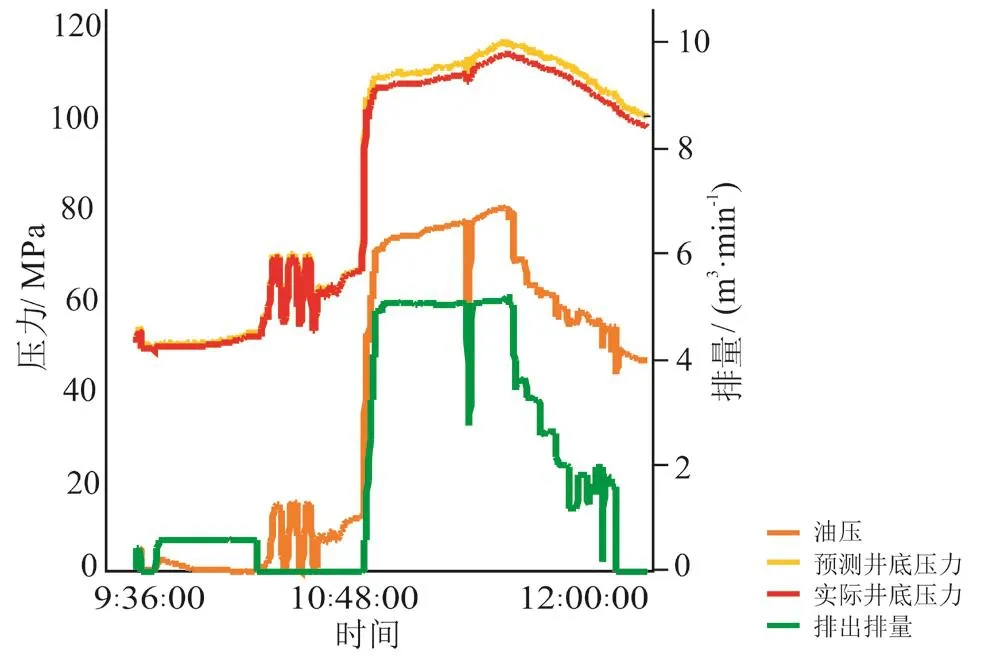
图4 GS111井井底压力预测结果对比情况图

表3 现场应用效果对比表

6 结论

1）相比于解析模型，BP神经网络方法能大幅提高酸化压裂井井底压力计算的准确性，有利于利用井底压力数据指导储层改造作业，提升改造效果。

2）建立的BP神经网络计算模型中，各输入参井酸化历史数据进行训练而来，为保证预测的准确性，推荐应用于本区域内近似井况的酸化井；如果需要扩大应用范围（如应用到加砂压裂井），则需要使用同井况气井的历史数据重新进行训练，以获得相应的神经网络。数影响井底压力计算结果的敏感程度依次为：液体流速＞液体黏度＞液体密度＞管柱内径。因此在利用BP神经网络方法计算井底压力时准确掌握液体排量和性能参数至关重要。

3）BP神经网络井底压力计算方法的适应范围、计算精度取决于训练期间使用的历史数据所覆盖的井况的范围以及数据量。

[ 1 ] 李达, 贾建鹏, 腾飞启, 朱更更, 吴明松. 压裂施工过程中的井底压力计算[J]. 断块油气田, 2013, 20(3)： 384-387.Li Da, Jia Jianpeng, Teng Feiqi, Zhu Genggeng & Wu Mingsong. Caculation of bottomhole pressure during fracturing[J].Fault-Block Oil & Gas Field, 2013, 20(3)： 384-387.

[ 2 ] 张广明, 刘合, 张劲, 吴恒安, 王秀喜. 水平井水力压裂的三维有限元数值模拟研究[J]. 工程力学, 2011, 28(2)： 101-106.Zhang Guangming, Liu He, Zhang Jin, Wu Heng'an & Wang Xiuxi. Three-dimensional fi nite element numerical simulation of horizontal well hydraulic fracturin[J]. Engineering Mechanics, 2011, 28(2)： 101-106.

[ 3 ] 李远照, 黄仲尧, 刘波, 刘俊. 运用井下压力数据评价压裂施工效果[J]. 天然气勘探与开发, 2007, 30(4)： 49-51.Li Yuanzhao, Huang Zhongyao, Liu Bo & Liu Jun. Apply downhole pressure to evaluating fracturing operation[J]. Natural Gas Exploration ＆ Development, 2007, 30(4)： 49-51.

[ 4 ] 李雪杉, 于春涛. 伊通盆地异常难压储层酸化技术[J]. 天然气勘探与开发, 2016, 39(1)： 60-62.Li Xueshan & Yu Chuntao. Acidif i cation technology for reservoirs with more fracturing challenges used in Yitong basin[J].Gas Exploration & Development, 2016, 39(1)： 60-62.

[ 5 ] 翁定为, 付海峰, 梁宏波. 水力压裂设计的新模型和新方法[J]. 天然气工业 , 2016, 36(3)： 49-54.Weng Dingwei, Fu Haifeng & Liang Hongbo. New models and methods for hydraulic fracturing design[J]. Natural Gas Industry, 2016, 36(3)： 49-54.

[ 6 ] 梁海波, 李欣嵘, 王玉. 基于神经网络的井底压力模型修正技术应用[J]. 自动化与仪表, 2012, 27(11)： 9-11.Liang Haibao, Li Xinrong & Wang Yu. Amending technology for drilling pressure model based on neural network[J]. Automation & Instrumentation, 2012, 27(11)： 9-11.

[ 7 ] 李昌盛, 宋海, 肖莉, 杨传书, 徐术国. 基于遗传算法优化BP神经网络的地层破裂压力预测方法[J]. 西安石油大学学报(自然科学版), 2015, 30(5)： 75-79.Li Changsheng, Song Hai, Xiao Li, Yang Chuanshu & Xu Shuguo. Prediction method of formation fracture pressure based on BP neural network optimized by genetic algorithm (GA)[J].Journal of Xi'an Shiyou University (Natural Science Edition),2015, 30(5)： 75-79.

[ 8 ] 李孝忠, 张有伟. 改进自适应遗传算法在BP神经网络学习中的应用[J]. 天津科技大学学报, 2010, 25(4)： 64-67.Li Xiaozhong & Zhang Youwei. Application of improvement self-adaptation genetic algorithm in BP neural network learning[J]. Journal of Tianjin University of Science & Technology,2010, 25(4)： 64-67.

[ 9 ]田旭光, 宋彤, 刘宇新. 结合遗传算法优化BP神经网络的结构和参数[J]. 计算机应用与软件, 2004, 21(6)： 69-71.Tian Xuguang & Song Tong & Liu Yuxin. Optimizing the structure and parameters of BP neural network based on genetic algorithm[J]. Computer Applications and Software, 2004, 21(6)：69-71.

[10] 王少波, 柴艳丽, 梁醒培. 神经网络学习样本点的选取方法比较[J]. 郑州大学学报(工学版), 2003, 24(1)： 63-65.Wang Shaobo, Chai Yanli & Liang Xingpei. Comparison of methods to produce sample points in training ANN[J]. Journal of Zhengzhou University (Engineering Science), 2003, 24(1)：63-65.