2-一致凸Banach空间的特征不等式*

李婷婷，苏雅拉图

(1. 内蒙古师范大学数学科学学院，内蒙古 呼和浩特010022；2. 准格尔民族小学，内蒙古 鄂尔多斯010300)

In 1936, the concept of a uniformly rotund Banach space was first introduced by Clarkson[1], and this class of Banach spaces is very interesting and has numerous applications. Consequently， some methods were found to investigate the geometry of Banach space (see [1]～[11] ). In 1977, Sullivan[2]introduced the 2-uniformly rotund spaces as a generalization of uniformly rotund Banach spaces.

In this paper,Xwill denotes a real Banach space andX*will denotes its dual space, symbols

U(X)={x:x∈X,‖x‖≤1},

S(X)={x:x∈X,‖x‖=1}

denote the unit ball and the unit sphere inXrespectively. For arbitrarily real numbersλ1,λ2,λ3,we always letλ1∨λ2∨λ3=max(λ1,λ2,λ3),λ∧λ2∧λ3=min(λ1,λ2,λ3),and for allλ1,λ2,λ3∈[0,1]are always assumed to be such thatλ1+λ2+λ3=1.

For an arbitrary spaceX,one of the measuring the “2-uniformly ”of the set of three dimensional subspaces is in terms of the real valued modulus of rotundity, i.e. forε>0,

Where

A(x1,x2,x3)=

Banach spaceXis said to be 2-uniformly rotund[2]if for anyε>0,there exists aδ>0, such that forx1,x2,x3∈S(X),if ‖x1+x2+x3‖>3-δ,thenA(x1,x2,x3)<ε.

In 1989, Zongben Xu and G. F. Roach [3] gave the characteristic inequality in the uniformly rotund Banach spaces as follows:Xis uniformly rotund Banach space if and only if for ∀p∈(0,1),there exists a strictly increasing functionδp(λ,μ,·):R+→R+,δp(λ,μ,0)=0, such that

‖λx+μy‖p+(‖x‖∨‖y‖)p·

λ‖x‖p+μ‖y‖p,∀x,y∈X

Where the symbol ‖x‖∨‖y‖means maximum of ‖x‖and ‖y‖, and ∀λ,μ∈[0,1] are satisfy thatλ+μ=1.

The generalization of above characteristic inequality to the 2-uniformly rotund Banach spaces which we shall consider can be motivated by the following restatement of the characteristic inequality in the uniformly rotund Banach spaces:Xis uniformly rotund Banach space if and only if for ∀p∈(0,1),there exists a strictly increasing functionδp(λ,μ,·):R+→R+,δp(λ,μ,0)=0, such that

‖λx+μy‖p+(‖x‖∨‖y‖)p·

λ‖x‖p+μ‖y‖p,∀x,y∈X

Where

Now we give the characteristic inequality in the 2-uniformly rotund Banach spaces as follows:Xis 2-uniformly rotund if and only if for each ∀p∈(0,1), there exists a strictly increasing functionδp(λ1,λ2,λ3,·):R+→R+,δp(λ1,λ2,λ3,0)=0,such that

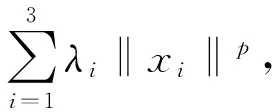
The characteristic inequality of 2-uniformly rotund Banach spaces.

Theorem1Xis 2-uniformly rotund if and only if for each ∀p∈(0,1), there exists a strictly increasing functionδp(λ1,λ2,λ3,·):R+→R+,δp(λ1,λ2,λ3,0)=0,such that

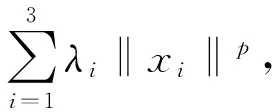
(1)

In order to prove theorem 1,we give two lemmas.

Lemma1[4]Xis 2-uniformly rotund Banach space if and only ifδX(ε)>0.

Lemma2 Forx1,x2,x3∈S(X),t1,t2∈(0,1],letε=A(x1,x2,x3)≠0,then

‖λ1x1+λ2t1x2+λ3t2x3‖≤

λ1+λ2t1+λ3t2-3(λ1∧λ2∧λ3)t1t2δX(ε)

Proof(I) Suppose thatx1,x2,x3are linearly independent and denote byEthe subspace spanned by the elementsx1,x2,x3and the zero element, then the elementλ1x1+λ2t1x2+λ3t2x3belongs toE. Letzbe the intersection point of the vectorλ1x1+λ2t1x2-x3and the rayτ·(λ1x1+λ2t1x2+λ3t2x3) in the subspaceE,whereτ≥0. Then there exist real numbersα,βsuch that

z=α(λ1x1+λ2t1x2+λ3t2x3),α≥0,

z=β(λ1x1+λ2t1x2)+(1-β)(λ1x1+

λ2t1x2+λ3x3), 0≤β≤1

Sincex1,x2,x3are linearly independent,it follows thatα=1,β=1-t2, and

‖λ1x1+λ2t1x2+λ3t2x3‖=

‖β(λ1x1+λ2t1x2)+(1-β)·

(λ1x1+λ2t1x2+λ3x3)‖≤

(1-t2)λ1+(1-t2)λ2t1+

t2‖λ1x1+λ2t1x2+λ3x3‖

Letwbe the intersection point of the rayτ·(λ1x1+λ3x3+λ2t1x2), (whereτ≥0) and the vectorλ1x1+λ3x3-x2.Then there exist real numbersμ,νsuch that

w=μ(λ1x1+λ3x3+λ2t1x2),μ≥0,

Sincex1,x2,x3are linearly independent, it follows thatμ=1,ν=1-t1,and

‖λ1x1+λ2t1x2+λ3x3‖=

Therefore

‖λ1x1+λ2t1x2+λ3t2x3‖≤(1-t2)λ1+

(1-t2)λ2t1+t2‖λ1x1+λ2t1x2+λ3x3‖≤

(1-t2)λ1+(1-t2)λ2t1+(1-t1)t2λ1+

(1-t1)t2λ3+t1t2‖λ1x1+λ2t1x2+λ3x3‖=

λ1+λ2t1+λ3t2-t1t2+

t1t2‖λ1x1+λ2t1x2+λ3x3‖

We define a function

where the symbolλ∧μmeans minimum ofλandμwithλ,μ∈[0,1],λ2+μ2≠0,andx,x1,x2∈X. Without loss of generality , we may assume thatλ3=min(λ1,λ2,λ3), then

f(λ2,λ3,x1,x2-x1,x3-x1)-

‖x1+x2+x3‖+3‖x1‖≤

Moreover, we have

≤

1-3λ3δX(ε)

Consequently,

‖λ1x1+λ2t1x2+λ3t2x3‖≤

λ1+λ2t1+λ3t2-3(λ1∧λ2∧λ3)t1t2δX(ε)

(2)

(II) Suppose thatx1,x2,x3are linearly dependent. BecauseA(x1,x2,x3)≠0,sox1,x2,x3are not all linearly dependent in pairs.

Ifλ1x1+λ2t1x2+λ3t2x3=0, then the conclusion is obviously.

Ifλ1x1+λ2t1x2+λ3t2x3≠0, it is impossible thatλ1x1+λ2t1x2andx3are collinear is simultaneous withλ1x1+λ3t2x3andx2are collinear. Otherwise, there exist real numbers,λ,μsuch that

λ1x1+λ2t1x2+λx3=0

(3)

λ1x1+μx2+λ3t2x3=0

(4)

From (3) and (4), we know thatx2andx3are non-collinear, it follows thatλ=λ3t2,μ=λ2t1.This is incompatible withλ1x1+λ2t1x2+λ3t2x3≠0.

① Whenλ1x1+λ2t1x2andx3are non-collinear,λ1x1+λ3t2x3andx2are collinear, denote byEthe subspace spanned by the elementsx1,x2,x3and the zero element, then the elementλ1x1+λ2t1x2+λ3t2x3belongs toE. Letzbe the intersection point of the vectorλ1x1+λ2t1x2-x3and the rayτ·(λ1x1+λ2t1x2+λ3t2x3) in the subspaceE, whereτ≥0. Then there exist real numbersα,βsuch that

z=α(λ1x1+λ2t1x2+λ3t2x3),α≥0

(5)

z=β(λ1x1+λ2t1x2)+(1-β)·

(λ1x1+λ2t1x2+λ3x3),0≤β≤1

(6)

(6)×α-(5), we have

αz-z=α(λ1x1+λ2t1x2+(1-β)λ3x3)-

α(λ1x1+λ2t1x2+λ3t2x3)=α(1-β-t2)λ3x3

Sincezandx3are linearly independent , it follows thatα=1,β=1-t2, and

‖λ1x1+λ2t1x2+λ3t2x3‖=

‖β(λ1x1+λ2t1x2)+

(1-β)(λ1x1+λ2t1x2+λ3x3)‖≤

(1-t2)λ1+(1-t2)λ2t1+

t2‖λ1x1+λ2t1x2+λ3x3‖

Fromλ1x1+λ3t2x3andx2are collinear, we know thatλ1x1+λ3x3andx2are non-collinear.

Letwbe the intersection point of the rayτ·(λ1x1+λ3x3+λ2t1x2), (whereτ≥0) and the vectorλ1x1+λ3x3-x2.Then there exist real numbersμ,νsuch that

w=μ(λ1x1+λ3x3+λ2t1x2),μ≥0

(7)

w=ν(λ1x1+λ3x3)+

(8)

(8)×μ-(7), we have

μw-w=μ(λ1x1+λ3x3+(1-ν)λ2x2)-

μ(λ1x1+λ3x3+λ2t1x2)=μ(1-ν-t1)λ2x2

Sincex2andware linearly independent, it follows thatμ=1,ν=1-t1,and

‖λ1x1+λ2t1x2+λ3x3‖=

Therefore

(1-t2)(λ1+λ2t1)+

(9)

By (2) we know that

(10)

Combining (9)and(10), we have

λ1+λ2t1+λ3t2-3(λ1∧λ2∧λ3)δX(ε)

② Whenλ1x1+λ2t1x2andx3are collinear,λ1x1+λ3t2x3andx2are collinear, we can prove it greatly similar to ①.

③ Whenλ1x1+λ2t1x2andx3are non-collinear,λ1x1+λ3t2x3andx2are non-collinear，from the process of proving (I) ,it follows that

‖λ1x1+λ2t1x2+λ3t2x3‖≤(1-t2)λ1+

(1-t2)λ2t1+t2‖λ1x1+λ2t1x2+λ3x3‖

Now we divide two possible cases:

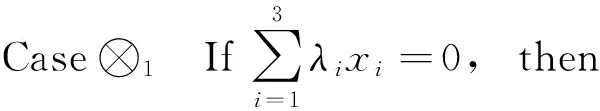
‖λ1x1+λ2t1x2+λ3t2x3‖≤(1-t2)λ1+

(1-t2)λ2t1+t2‖λ1x1+λ2t1x2+λ3x3‖=

(1-t2)λ1+(1-t2)λ2t1+t2(λ2-λ2t1)=

λ1+λ2t1+λ3t2-2λ2t1t2-(λ1+λ3-λ2)t2≤

λ1+λ2t1+λ3t2-2λ2t1t2-(λ1+λ3-λ2)t1t2=

λ1+λ2t1+λ3t2-t1t2≤

λ1+λ2t1+λ3t2-t1t2δX(ε)≤

λ1+λ2t1+λ3t2-3(λ1∧λ2∧λ3)t1t2δX(ε)

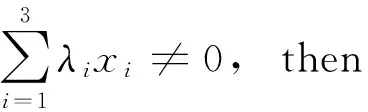
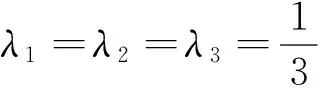
Which implies that

Thus, applying Lemma 1, we know thatXis 2-uniformly rotund Banach space.

Conversely, suppose thatXis a 2-uniformly rotund Banach space. We shall construct a functionδp(λ1,λ2,λ3,ε), so that the inequality (1) is fulfilled. For this purpose, we first define a function

where

Now we show the following inequality:

‖λ1x1+λ2x2+λ3x3‖p+φp(λ1,λ2,λ3,ε)≤

λ1‖x1‖p+λ2‖x2‖p+λ3‖x3‖p

with the functionδp(λ1,λ2,λ3,ε)holds for every ∀x1∈S(X),x2,x3∈U(X).

Let

‖x1‖=1,‖x2‖=t1,

and consider the functiongdefined by

g(t,t′)=

λ1+λ2tp+λ3t′p-(λ1+λ2t+λ3t′-

0≤t,t′≤1

From Lemma 2, we have

λ1‖x1‖p+λ2‖x2‖p+

λ3‖x3‖p-‖λ1x1+λ2x2+λ3x3‖

(11)

In what follows, we will divide four possible cases which complete the steps of proving theorem 1.

Let

then

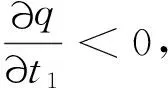
(λ1+λ2t1+λ3t2)p≥

and

Because

(λ1+λ2t1+λ3t2)p≥

Indeed,

It follows that

Because the functionδX(ε) is strictly increasing inε,so we have

(λ1+λ2t1+λ3t2-

From

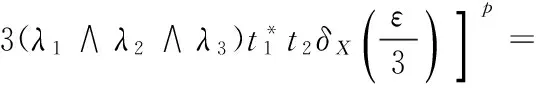
Hence

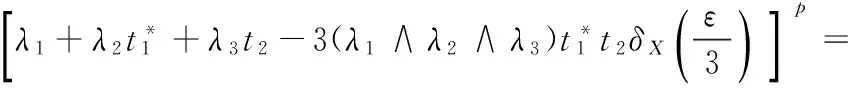
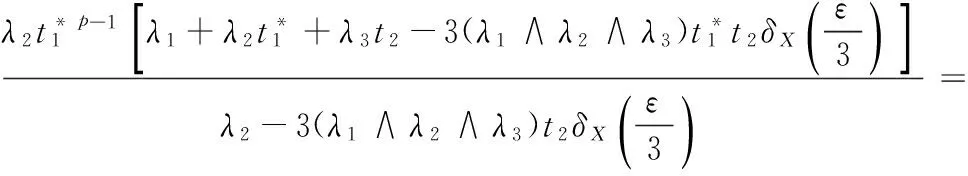
Hence

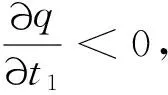
(λ1+λ2t1+λ3t2)p≥

and

From

Hence

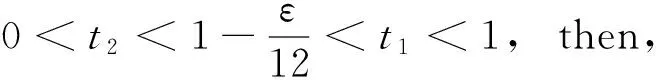
(λ1+λ2t1+λ3t2)p≥

Hence

Combining these inequalities with (11), we have that

‖λ1x1+λ2x2+λ3x3‖p+φp(λ1,λ2,λ3,ε)≤

λ1‖x1‖p+λ2‖x2‖p+λ3‖x3‖p

for

∀x1∈S(X) andx2,x3∈U(X)

Let

δp(λ1,λ2,λ3,ε)=

min{φp(λ1,λ2,λ3,ε),

φp(λ2,λ1,λ3,ε),φp(λ3,λ2,λ1,ε)}

then ，for eachp∈(0,1),there exists a strictly increasing functionδp(λ1,λ2,λ3,·):R+→R+,

δp(λ1,λ2,λ3,0)=0,such that

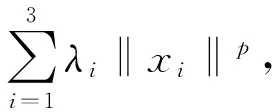
参考文献：

[1] CLARKSON J A. Uniformly convex spaces [J]. Trans Amer Math Soc, 1936, 40: 396-414.

[2] SULLIVAN F. A generalization of uniformly rotund Banach spaces [J]. Canad J Math, 1979,31: 628-636.

[3] XU Z B, ROACH G F. Characteristic inequalities of uniformly convex and uniformly smooth Banach spaces [J]. J Math Anal Appl, 1991, 157: 189-210.

[4] YU X T. Geometric theory of Banach space [D]. Shanghai: East China Normal University, 1984.

[5] GEREMA R, SULLIVAN F. Multi-dimensional volumes and moduli of convexity in Banach spaces [J]. Ann Math Pure Appl, 1981,127: 231-251.

[6] KIRK W A, SIMS B. Handbook of metric fixed point theory [M]. Dordrecht:Kluwer Acad Publ, 2001.

[7] MITRINOVIC D S, PEUCARIC J E, FINK A M. Classical and new inequalities in analysis [M]. Dordrecht: Kluwer Acad Publ, 1993.

[8] 黎永锦，林洁珠. 连续线性泛函与Banach 空间的凸性[J]. 中山大学学报(自然科学版)，2006, 45(1): 17-19.

LI Y J, LIN J Z. Bilinear continuous functional and convexity of Banach spaces [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2006, 45(1): 17-19.

[9] 华柳斌，黎永锦. 2-赋范空间和拟Banach 空间中的华罗庚不等式[J]. 中山大学学报(自然科学版)，2009, 48(3): 13-15.

HUA L B, LI Y J. Hua Lo-Keng inequality in 2-normed spaces and quasi-Banach spaces [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2009, 48(3): 13-15.

[10] 黎永锦，舒小保.k-弱凸性与k-弱光滑性[J]. 中山大学学报(自然科学版)，2002, 41(5): 8-10.

LI Y J, SHU X B.k-weakly convex andk-weakly smooth [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2002, 41(5): 8-10.

[11] 冼军，黎永锦，赵志红. 中点局部k-一致凸性和φ-直和[J]. 中山大学学报(自然科学版), 2005, 44(6):1-4.

XIAN J, LI Y J, ZHAO Z H. Midpoint locallyk-uniform convexity andφ-direct sum [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2005, 44(6):1-4.