基于支持张量机算法和3D脑白质图像的阿尔兹海默症诊断*

徐盼盼，杨宁，李淑龙

(1. 南方医科大学生物医学工程学院∥广东省医学图像处理重点实验室，广东 广州 510515;2. 广东省第二人民医院，广东 广州 510317)

阿尔兹海默症[1](Alzheimer’s disease，AD)是一种中枢神经系统变性病，起病隐袭，病程呈慢性进行性；病理上表现为脑体积缩小和重量减轻，脑沟加深，脑回萎缩；临床表现为渐进性记忆障碍、认知功能障碍以及语言障碍等症状，是老年期痴呆中最常见的一种类型。2017年统计资料统计显示，在各种死亡原因中，AD占第8位[2]。AD不仅严重影响患者的生活质量，而且给患者家庭和社会带来沉重的精神和经济负担。研究表明，如果在AD早期阶段对患者进行干预治疗，可延缓AD发病时间[3]。然而AD的早期诊断非常困难，确诊时一般已经达到中晚期，治疗效果显著下降。Petersen等[4]的研究指出，轻度认知障碍(Mild Cognitive Impairment, MCI)是AD的前驱阶段，可认为是AD发病的早期信号，对MCI进行深入研究，可以筛选出AD的高危人群，为治疗提供最佳时间。因此对AD疑似患者做风险分层预测具有很重要的临床意义。

基于医学影像的计算机辅助诊断是医学发展的一大趋势，其核心是建立一个行之有效的分类算法。近年来，线性判别分析(LDA)、独立成分分析(ICA)、支持向量机(SVM)等分类算法有效地用于阿尔兹海默症的诊断研究。然而这些方法都先把本质上具有3D张量结构的图像数据展开成向量，这样不但会造成空间结构信息的丢失，而且向量化之后的特征维数大大增加，容易造成小样本事件与维数灾难。随着张量数据的有效表达以及多线性空间优化理论的发展，张量空间模型得到广泛的发展及有效应用。Yang等[5]提出二维主成分分析(2DPCA)算法，直接提取原始矩阵数据的协方差矩阵的特征向量作为图像的特征，与传统PCA相比，不仅保持了原始数据的结构特征，而且提高了运算效率。Yan等[6]提出基于张量表示的判别分析方法，将目标数据用二阶或高阶张量表示，然后将张量数据按其中某一模展开，展开后矩阵的列向量是与原张量数据有相同标记的新的目标数据，然后进行聚类判别分析。Liu等[7]提出了张量空间模型(TSM)的概念，并将其运用到信息检索方面。Tao等[8-9]提出并完善了有监督的张量学习框架(STL)，把传统机器学习中的向量输入改为张量输入，用交替投影算法求最优解，并提出支持张量机(Support Tensor Machine, STM)等学习模型。杨宁等[10]将支持张量机模型用于阿尔兹海默症的脑图像分类，并结合张量的独立成分分析算法，取得了较好的分类结果。

近年来基于脑灰质图像的AD预测研究已取得了较大进展[10-12]，然而关于脑白质图像的研究几乎是空白。白质异常不仅代表AD的早期神经病理学事件，而且可能在AD的发病机制和诊断中起重要作用[13-15]。本文提出一种以3D T1加权MR脑白质图像为输入的基于支持张量机的阿尔兹海默症分类算法。首先把T1加权MR脑图像分割成灰质、白质、脑脊液3部分；然后提取脑白质灰度信息构建三阶张量；接着利用支持张量机迭代算法训练张量样本3个模的权向量并结合递归特征消除法(Recursive feature elimination, RFE)进行特征选择；最后用支持张量机进行分类。

1 试验材料与方法

1.1 样本数据

本文共收集70例AD患者、112例MCI患者 (包含56例在随访中转化为AD的，MCI-C: MCI Converters；56例在随访中未转化为AD的，MCI-NC: MCI Non-converters)以及70例NC(正常人)的MRI数据。所有数据均来自于阿尔兹海默症神经影像学组织(Alzheimer’s Disease Neuroimaging Initiative, ADNI)数据库http:/ /www. adni. loni. usc.edu。

每组测试人群满足的标准如下[23]：(i) NC组:简明精神状态检查量表(mini-mental state examination, MMSE)评分为24～30，临床痴呆等级(Clinical Dementia Rating , CDR)等于0，非抑郁，非MCI，非痴呆；(ii) MCI组：MMSE评分为24～30，CDR等于0.5，韦式记忆量表逻辑记忆测试表明有客观记忆力减退，其他认知领域无明显损伤，基本保留了日常生活能力，非痴呆；(iii) AD组：MMSE评分为20～26，CDR等于0.5或1，符合美国国立神经病语言障碍卒中研究所(NINCDS)和阿尔兹海默症及相关疾病协会(ADRAS)对于可能患AD所定义的标准[16]。研究对象的详细信息如表1。

表1 研究对象信息1)Table1 The information of research subjects

1)MMSE: mini-mental state examination；ADAS-Cog: Alzheimer’s Disease Assessment Scale-cognitive subscale.

1.2 张量构造

采用SPM8软件(http:∥www. fil. ion. ucl. ac. uk/spm/software/spm8/)中的VBM8工具箱[17]将T1加权MRI进行配准、平滑及空间归一化处理，并把全脑图像自动分割为灰质、白质与脑脊液3部分。提取分割后的脑白质各体素的灰度值，构建大小为84×74×75三阶灰度张量。

2 实验方法

2.1 张量概念及张量的基本运算

1)张量概念

张量也称为多维数组[18]，是向量和矩阵的高阶推广，一阶张量是向量，二阶张量是矩阵。在高阶张量中，阶数代表了张量的复杂程度。对于任意一个N阶张量X=(xl1,l2，…，lN)∈RL1×L2×…×LN,Xl1,l2，…，lN(1≤li≤Li,1≤i≤N)，表示X张量在位置(l1,l2,…，lN)处的元素值。

2)张量的基本运算

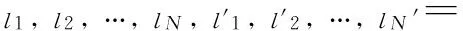
(1)

定义2(模-n纤) 改变第n模索引值而固定其它模索引所得到的向量。二阶张量的行向量是模-1纤，列向量是模-2纤；三阶张量有模-1纤，模-2纤，模-3纤，各模纤如图1所示：

定义3(张量的模-n展开) 张量的模-n展开是把张量中的元素重新排成矩阵的过程。对于任意N阶张量X∈RL1×L2×…×LN的模-n展开，假设张量在位置(l1,l2,…，lN)上的元素映射到矩阵中元素的位置为(ln,l)，则

(2)

三阶张量模-1展开的过程如图2所示：

定义4(模-n积) 张量X∈RL1×L2×…×LN和矩阵U∈RLn′×Ln的模-n积(记为X×nU)是空间RL1×L2×…×Ln-1×Ln′×…×LN中的张量，所得张量的元素为每个模-n向量与矩阵U的乘积，即：

图1 三阶张量 (a) 模-1纤；(b) 模-2纤；(c) 模-3纤Fig.1 Third-order tensor (a) mode-1 fiber; (b) mode-2 fiber; (c) mode-3 fiber

图2 三阶张量模-1展开过程Fig.2 The process of third-order tensor expands into matrix based on mode-1

(3)

三阶张量与矩阵的模-1积如图3所示：

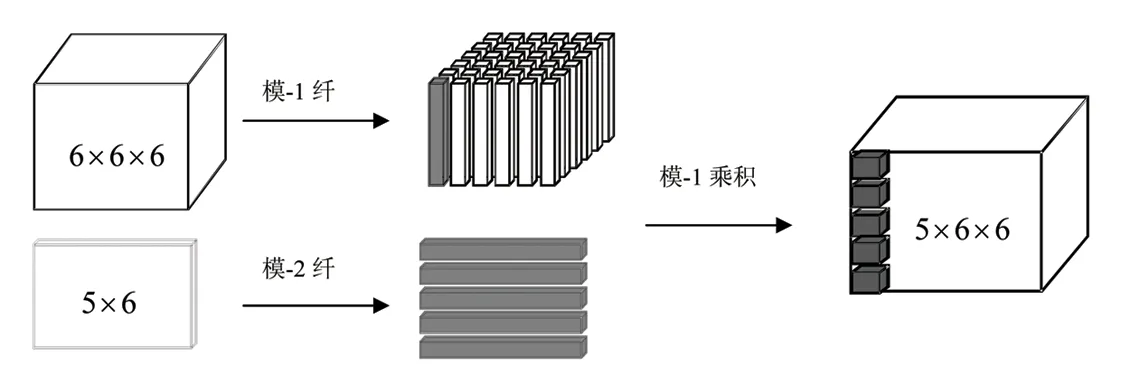
图3 三阶张量与矩阵的模-1积Fig.3 The mode-1 product of third-order tensor and matrix

2.2 支持张量机(Support Tensor Machine, STM)

Corinna Cortes等[19]在1995年提出了支持向量机(Support Vector Machine，SVM)的概念，它以结构风险最小化为准则，并引入了核函数，在解决小样本、高维数、非线性、局部极小点等问题中发挥了重要作用。然而支持向量机以向量样本为输入，在处理高维数据问题时具有局限性。2005年，Tao等[8]在研究张量表示的小样本分类预测问题时首次提出支持张量机的思想，该方法直接以张量数据为输入，旨在张量空间找到一个最优的分类张量超平面，使得两类支持张量(离张量超平面最近的张量)之间在允许少量分类误差的情况下具有最大的间距。

给定高阶张量训练样本{Xi,yi},i=1,2,…，M，其中Xi∈RL1×L2×…×LN为N阶张量数据，yi为样本对应的分类标签，M为训练样本数量。构造分类超平面：

(5)

其中wk∈RLk,k=1,2,…，N,b∈R为待训练参数，×k为张量与向量的模积符号。取离张量超平面(5)最近的训练样本到超平面的间隔为1，则对于所有训练样本有

(6)

允许少数离群点的存在，引入松弛变量ξ及惩罚因子C，得到如下优化问题：

(7)

满足：

(8)

(ξi≥0,i=1,2,…,M)

(9)

用交替投影算法求解最优化问题(7)-(9)，具体步骤如下；

步骤1：初始化w1,w2,…，wN为全为1的向量；

步骤2：j=N；

(10)

满足：

(11)

(ξi≥0,i=1,2,…,M)

(12)

这是标准支持向量机的分类模型，运用拉格朗日对偶方法即可求解出新的wj，b并更新wj；

步骤4：令j=j-1重复步骤3，直到j=1，计算出所有wk,k=1,2,…,N；

步骤5：重复步骤2，3，4，直到上次循环与本次循环得到的wk和b充分接近。

由式(7)-(9)所定义的最优化问题一旦被解，则张量超平面(5)就被确定，而对于张量样本可由以下分类函数来预测

(13)

从上面的步骤可以看出，支持张量机其实是N个支持向量机的迭代过程。不同的是，支持张量机直接将原始的高阶张量作为输入，这样既保持了数据的结构信息，又可以避免数据向量化可能造成的维数灾难和小样本事件。

2.3 递归特征消除法(Recursive Feature Elimination, RFE)

对于小样本高维度的分类问题，特征选择在避免过拟合和提高分类性能方面起着重要作用。陈振洲等[20]指出，要根据与分类的相关性赋予特征不同的权重，强相关的赋予较高权重，弱相关的赋予较低权重，不相关的赋予0权重。Guyon等[21]提出递归特征消除算法(Recursive Feature Elimination, RFE)并用于癌症细胞分类，它是一种逐步消除冗余或者与分类不相关的信息的特征选择方法，通常与分类器结合使用。其中与支持向量机相结合的SVM-RFE算法是常用的特征选择方法，它通过支持向量机训练模型并测试，计算每个特征的排序准则分数，去掉得分最小的特征，然后用剩余的特征再次训练测试，进行下一次迭代选择，最后选出最优特征子集。

本文所用是递归特征消除算法与支持张量机相结合的STM-RFE特征选择方法。对于高阶张量训练样本{Xi,yi},i=1,2,…,M，假设支持张量机训练出来的各模的特征权向量为wk,k=1,2,…,N，则算法具体步骤如下：

步骤1：j=N；

步骤2：初始化模-j原始特征索引集合dj=[1,2,…,nj]，输出特征排序rj=[]；

步骤4：选择特征子集

步骤5：用新的特征子集作为支持向量机的输入，训练模型获得特征权向量w；

步骤6：对于每一种特征子集，计算其准则分数score=(w)2；

步骤7：找出特征排序准则分数最小的特征索引dj(l)，并更新rj=[dj(l),rj]；

步骤8：消除特征排序准则分数最小的特征，dj=dj[1∶l-1,l+1:length(dj)]；

步骤9：重复步骤4-8，直至dj=[];

步骤10：输出特征排序表rj；

步骤11：令j=j-1，重复步骤2-10，直到j=1，得到所有模的特征排序rj,j=1,2,…,k。

需要注意的是，特征排序系数较大的那些特征，单个特征并不一定能获得较好的分类结果，有时需要多个特征的组合才能达到目的。我们利用特征排序列表，定义若干嵌套的特征子集F1⊂F2⊂…⊂Fn来训练支持向量机，并以支持向量机的预测正确率来评估这些子集的优劣，从而获得每个模的最优特征子集。

2.4 实验框架

本文实验的流程框图如图4所示：①用SPM8软件将采集的T1加权MR脑图像配准到标准模板空间；②借助工具箱提供的分割模型，全脑图像被自动分割成灰质、白质、脑脊液3部分；③提取脑白质各体素的灰度值构建三阶灰度张量；④用递归特征消除法结合支持张量机进行特征选择；⑤用支持张量机进行分类。

我们对以下4种情况进行预测：AD vs NC,AD vs MCI,MCI vs NC, MCI-C vs MCI-NC，并用10折交叉验证方法评估实验结果，用准确率(ACC)，敏感性(SEN)，特异性(SPE)以及ROC曲线下面积(AUC)4个指标评价分类器的性能。令TP,TN,FP,FN分别代表真阳性，真阴性，假阳性，假阴性的数目，那么

由于实验中存在样本不均衡的问题(阿尔兹海默症患者和正常对照组分别为70例，轻度认知障碍患者组112例)，本文采用SMOTE算法[22](synthetic minority over-sampling technique)合成新的小类样本以解决这一问题。

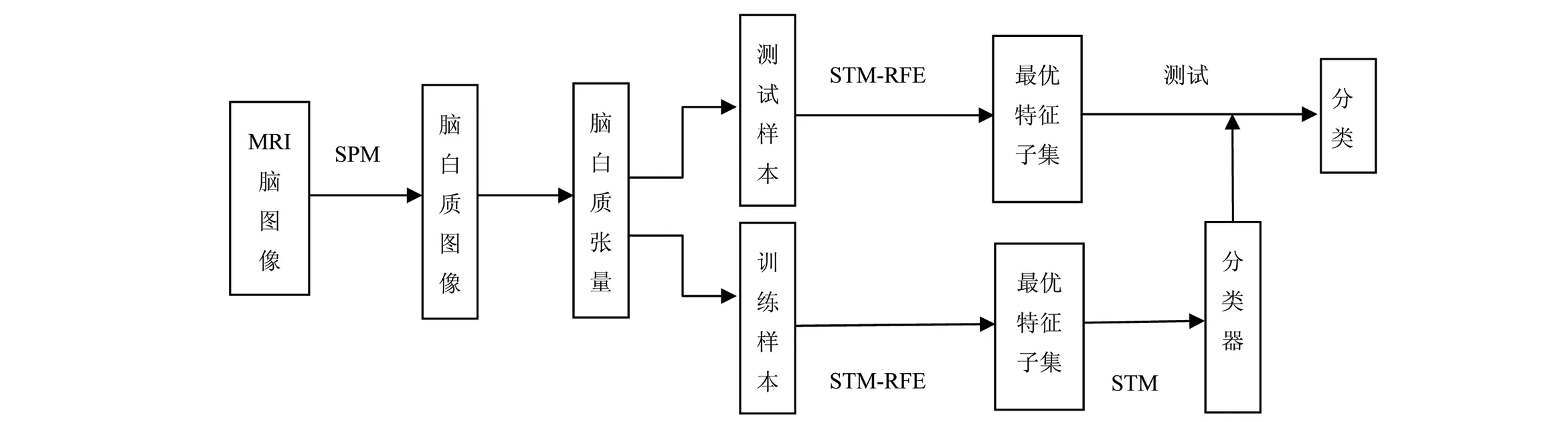
图4 流程框图Fig.4 The flow chart of experiment

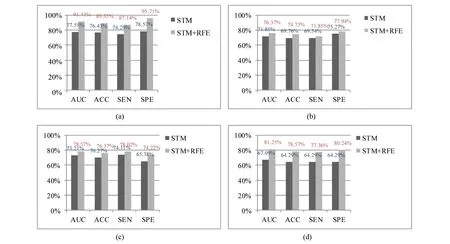
图5 STM与STM+RFE对比实验结果Fig.5 The comparisons between STM and STM+RFE(a) AD vs NC; (b) AD vs MCI; (c) MCI vs NC; (d) MCI-C vs MCI-NC

3 结果与讨论

本文实验以脑白质图像的灰度张量特征为输入，分别用支持张量机作为分类器和先用STM-RFE进行特征选择再用支持张量机分类两种方法进行，结果如图5所示。从图5可以看出：用递归特征消除算法进行特征选择之后，4组实验人群的分类结果都有了显著的提高。特别是，AD vs NC和MCI-C vs MCI-NC这两组中ROC曲线下面积(AUC)、准确率(ACC)、敏感性(SEN)、特异性(SPE)分别都提高了10%以上。由此得出结论：递归特征消除算法有效的剔除了一些冗余信息并选择出了最优特征子集，提高了分类器的性能。

研究表明多模态特征结合可以提高AD的检出率[23-25]，然而这也就意味着患者需要做脑脊液(CSF)，PDG-PET等大量复杂而昂贵的检查，给患者造成沉重的精神及经济负担。临床上，医生通常会给患者做一些简单的神经心理学测试作为辅助诊断依据，比如简易精神状态检查表(MMSE: mini-mental state examination)、阿尔兹海默症认知评估量表(ADAS-Cog: Alzheimer’s Disease Assessment Scale-cognitive subscale)。我们将MMSE和ADAS-Cog称之为认知分数。患者的基本信息(年龄、性别、教育程度)也有可能为AD诊断提供了一些有用的信息，所以我们在灰度张量特征的基础上加入了样本的认知分数和基本信息进行实验。同时观察以基本信息，或认知分数作为支持向量机输入进行分类的结果，并跟灰度张量结合认知分数，灰度张量结合认知分数和基本数据作为支持张量机的输入的实验结果进行比较，结果如表2所示。表2中方法a表示以基本信息为支持向量机输入进行分类的结果；方法b表示以认知分数为支持向量机输入进行分类的结果；方法c代表以灰度张量为支持张量机输入进行分类的结果；方法d表示结合灰度张量和认知分数，先用STM-RFE算法做特征选择，最后用支持张量机进行分类的结果；方法e表示结合灰度张量、认知分数和基本数据，先用STM-RFE算法做特征选择，最后用支持张量机进行分类的结果。每组实验所对应的ROC曲线如图6所示。

表2 加入不同特征的实验结果Table 2 The results of different characteristics %

图6 ROC曲线Fig.6 The ROC curves

从表2和图6中可以看出，单个特征中，认知分数和灰度张量特征对分类起了很大作用，而多种特征相结合，分类准确率大于单个特征。这说明多种模态特征之间提供了互补的信息，将这些特征结合在一起可以提高分类器的性能。

为了体现本文所提出的算法的有效性，我们将不同文献的结果进行比较,结果如表3所示。Khedher等[26]提出独立成分分析和支持向量机相结合的MRI数据自动分类方法：首先用独立成分分析算法分别提取脑白质和脑灰质的独立成分，然后将两者相结合并用支持向量机在3组人群中进行分类测试，AD vs NC组的分类准确率达到86.37%；Xin等[27]提出了基于局部线性嵌(LLE)的阿尔兹海默症分类算法，提取94个感兴趣区的体素特征和68个皮层厚度特征，用LLE算法对高维特征进行降维，然后用3种不同的分类器进行测试，其中AD vs NC的分类准确率达到90%，MCI-C vs MCI-NC的分类准确率达到了68%。Zhang等[23]对MRI，PDG-PET，CSF生物标志物3种模态的特征进行融合，再用线性支持向量机进行分类，AD vs NC的分类准确率达到93.2%。从表3的结果可以看出，我们的算法在3组实验人群中都取得了比较好的结果，在比较难以区分MCI-C和MCI-NC组，也取得了82.08%的分类准确率，所以可以认为本文提出的算法具有可行性。

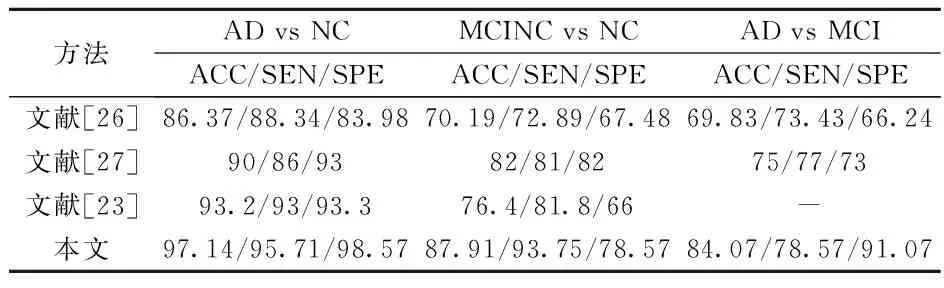
表3 不同文献算法对比Table 3 The comparison of different literature %

4 结 论

本文提出一种以3D T1加权MR脑白质图像为输入的基于支持张量机的阿尔兹海默症分类法。我们首先利用SPM8软件中的VBM8工具箱把全脑图像自动分割为灰质、白质、脑脊液3部分；然后提取脑白质各体素灰度值，构建三阶灰度张量；接着用递归特征消除法结合支持张量机进行特征选择；最后用支持张量机进行分类。与传统的向量空间的机器学习相比，本文提出的算法以原始的高阶张量图像数据作为输入，保持了数据结构信息的完整性，也避免了因数据向量化可能造成的小样本事件与维数灾难；另外，本算法使用了递归特征消除与支持张量机相结合的特征选择算法，有效剔除了冗余信息并选出最优子集，提高了分类器的性能；此外，本文在MRI数据的基础上结合样本的基本信息和认知数据，取得了较好的分类结果。实验结果证明，本文提出的算法可以有效的识别AD和MCI患者。

参考文献：

[1] WM V D F, SCHELTENS P. Epidemiology and risk factors of dementia [J]. J Neurol Neurosury Psychiatry, 2005, 76 (Suppl V): 2-7.

[2] SIEGEL R L, MILLER K D, JEMAL A. Cancer statistics, 2017 [J]. Ca: A cancer journal for clinicians, 2017, 67(1):7-30.

[3] BROOKMEYER R, GRAY S, KAWAS C. Projections of Alzheimer’s disease in the United States and the public health impact of delaying disease onset [J]. American Journal of Public Health, 1998, 88(9):1337-1342.

[4] PETERSEN R C. Mild cognitive impairment as a diagnostic entity [J]. Journal of Internal Medicine, 2004, 256(3): 183-194.

[5] YANG J, ZHANG D, FRANGI A F, et al. Two-dimensional PCA: a new approach to appearance-based face representation and recognition [J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2004, 26(1): 131-137.

[6] YAN S, XU D, YANG Q, et al. Discriminant analysis with tensor representation [C]∥Computer Vision and Pattern Recognition, 2005. CVPR 2005. IEEE Computer Society Conference on. IEEE, 2005, 1:526-532.

[7] LIU N, ZHANG B, YAN J, et al. Text representation: from vector to tensor [C]∥ IEEE International Conference on Data Mining. IEEE Computer Society, 2005: 725-728.

[8] TAO D, LI X, HU W, et al. Supervised tensor learning [C]∥ IEEE International Conference on Data Mining. IEEE Computer Society, 2005: 450-457.

[9] TAO D, LI X, WU X, et al. Supervised tensor learning [J]. Knowledge and Information Systems, 2007, 13(1): 1-42.

[10] 杨宁，徐盼盼，刘佩嘉，等. 基于张量法的阿尔兹海默症脑图像分类[J]. 中山大学学报(自然科学版), 2017, 56(2): 40-47.

YANG N, XU P P, LIU P J, et al. Prognostic classification of Alzheimer’s disease brain image based on tensor method [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2017, 56(2): 40-47.

[11] FRISONI G B, TESTA C, ZORZAN A, et al. Detection of grey matter loss in mild Alzheimer’s disease with voxel based morphometry [J]. J Neurol Neurosurg Psychiatry, 2002, 73(6): 657-664.

[12] CHÉTELAT G, DESGRANGES B, LANDEAU B, et al. Direct voxel-based comparison between grey matter hypometabolism and atrophy in Alzheimer’s disease [J]. Brain A Journal of Neurology, 2008, 131(Pt 1): 60.

[13] BOZZALI M, FALINI A, FRANCESCHI M, et al. White matter damage in Alzheimer’s disease assessed in vivo using diffusion tensor magnetic resonance imaging [J]. Journal of Neurology Neurosurgery & Psychiatry, 2002, 72(6): 742-746.

[14] DI P M, LUDERS E, DI I F, et al. Callosal atrophy in mild cognitive impairment and Alzheimer’s disease: different effects in different stages [J]. Neuroimage, 2010, 49(1): 141-149.

[15] SACHDEV P S, ZHUANG L, BRAIDY N, et al. Is Alzheimer’s a disease of the white matter? [J]. Current Opinion in Psychiatry, 2013, 26(3): 244.

[16] MCKHANN G, DRACHMAN D, FOLSTEIN M, et al. Clinical diagnosis of Alzheimer’s disease [J]. Neurology, 1984, 34(2):1097-1105.

[17] EGGERT L D, JENS S, ANDREAS J, et al. Accuracy and reliability of automated gray matter segmentation pathways on real and simulated structural magnetic resonance images of the human brain [J]. PLoS One, 2012, 7(9): e45081.

[18] 孙明芳. 基于张量的图像识别方法的研究[D].长春：吉林大学，2012.

SUN M F. The research of image recognition method based on tensor [D]. Changchun: Jilin University, 2012.

[19] CORTES C, VAPNIK V. Support-vector networks [J]. Machine Learning, 1995, 20(3): 273-297.

[20] 陈振洲, 李磊, 姚正安. 基于SVM的特征加权KNN算法[J]. 中山大学学报(自然科学版), 2005, 44(1): 17-20.

CHEN Z Z, LI L, YAO Z A. Feature-weighted k-nearest neighbor algorithm with SVM [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2005, 44(1): 17-20.

[21] GUYON I. Erratum: Gene selection for cancer classification using support vector machines [J]. Machine Learning, 2001, 46(1/2/3): 389-422.

[22] CHAWLA N V, BOWYER K W, HALL L O, et al. SMOTE: synthetic minority over-sampling technique [J]. Journal of Artificial Intelligence Research, 2002, 16(1): 321-357.

[23] ZHANG D, WANG Y, ZHOU L, et al. Multimodal classification of Alzheimer’s disease and mild cognitive impairment [J]. Neuroimage, 2011, 55(3): 856-867.

[24] HINRICHS C, SINGH V, XU G, et al. Predictive markers for AD in a multi-modality framework: an analysis of MCI progression in the ADNI population [J]. Neuroimage, 2011, 55(2): 574-589.

[25] WILLETTE A A, CALHOUN V D, EGAN J M, et al. Prognostic classification of mild cognitive impairment and Alzheimer’s disease: MRI independent component analysis [J]. Psychiatry Research Neuroimaging, 2014, 224(2): 81-88.

[27] XIN L, DUYGU T, WEINER M W, et al. Locally linear embedding (LLE) for MRI based Alzheimer’s disease classification [J]. Neuroimage, 2013, 83: 148-157.