基于聚类分析的铝电解槽阳极压降的分类

吴荣强，李晋宏

（北方工业大学计算机学院 知识工程研究所，北京 100144）

0 引言

本文采用的阳极压降数据是某铝厂利用新型的阳极压降信号采集装置采集到的阳极压降。铝电解槽中阳极导杆分为A，B两侧，A侧和B侧各有8块阳极。每个位置的阳极导杆的压降波动情况都有所差异，每个位置的阳极都要经历换极，换极的周期大致为28天左右，换极质量的好坏会严重影响整个电解槽槽电压的稳定。对阳极压降进行聚类分析，能够合理分析电压波动情况，避免某次换极影响电解槽，并且对电解槽的有效生产和减少损耗有一定的益处[1-2]。

目前对电解槽阳极压降的研究已经有了一些进展。林立明等在文献中[3]通过提取在同一个电解槽中不同阳极导杆的电流的频谱特征，分别利用功率谱估计方法和因子分析方法对其进行分析，得到同一电解槽中 A，B两侧磁场呈现不同分布状态。但是未对时间序列的阳极电压异常波动和分布特性进行挖掘。刘永强等在文献中[4]分析了铝电解槽在生产过程中阳极炭块在出现脱落，偏流和阳极长包等异常情况下，电压的波动状态，并且给出了相应的异常处理方式。但这种方式只是发现异常情况下的电压波动情况，并未进行阳极换极周期性电压波动的分析。本文通过对电解槽A，B两侧16根阳极周期数据进行分析，提取阳极换极后的上升期长度，阳极压降速升次数，速升平均幅度，速降次数，速降平均幅度，以及影响因子特征，并利用聚类方法对这6维数据进行聚类，挖掘不同位置阳极相似的电压波动情况，在一定程度上对阳极换极后的质量进行评估。

1 阳极电压特征分析

1.1 数据描述

本文的数据来源于某铝厂的4622号电解槽A，B两侧的阳极导杆的压降值，该数据是通过采集器每5s采集的一组数据。数据采集的频率过高，随着时间的增加，阳极压降的数据量巨大，直接对阳极压降原始数据进行欧式距离计算复杂度较高，需要对原始数据进行特征抽取，降低维度再进行距离计算会大大降低复杂度[5-6]。原始数据如图1所示。

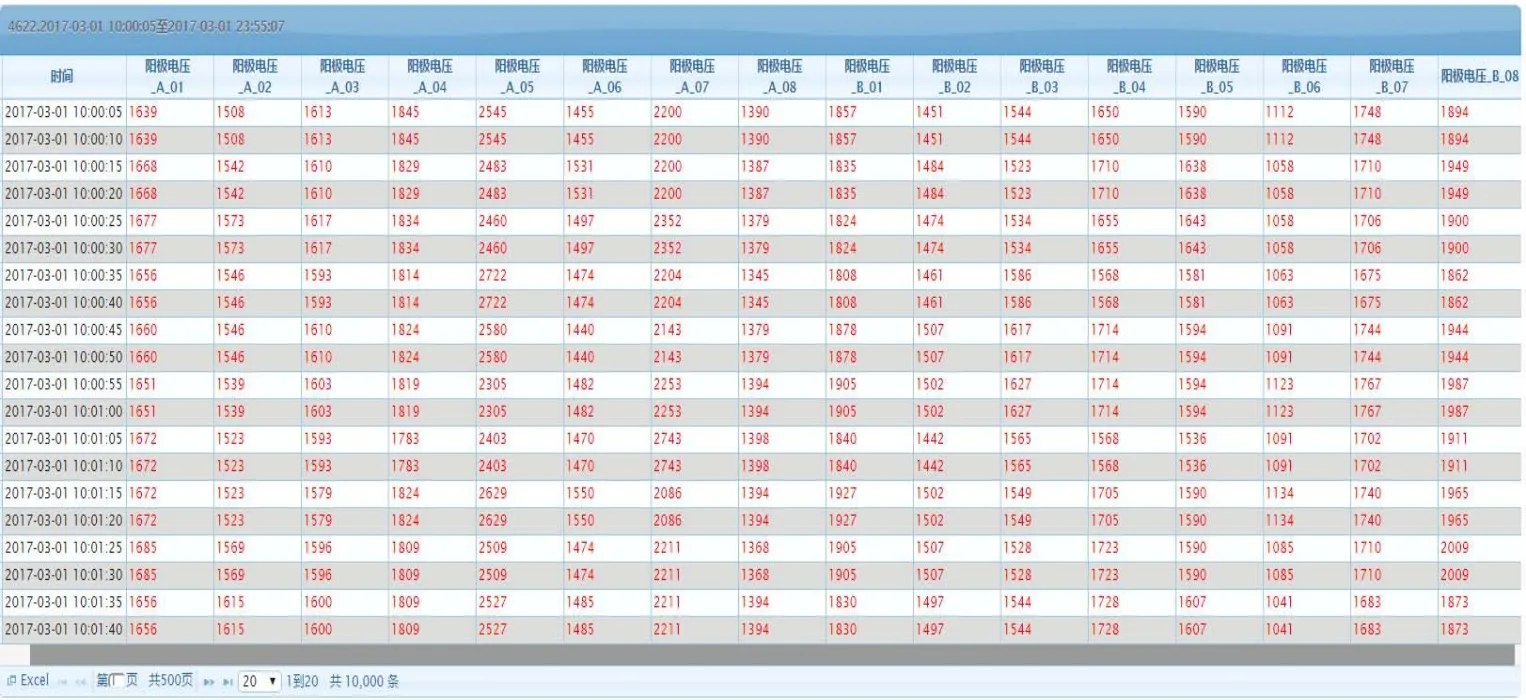
图1 阳极压降原始数据Fig.1 Anode voltage drop raw data

1.2 特征提取

（1）阳极换极上升期长度

电解槽中每个阳极都有一定的生命周期，一般是在 28天左右，每次换极电压值会下降到 50 mv左右，再经过一段时间的恢复期，电压值会达到1500 mv左右的平稳期。所以需要从原始数据中自动获取每次换极的时刻和到达平稳期的时刻，从而计算出阳极换极上升期跨度的时间值即长度。利用滑动窗口算法[7-9]，每个窗口大小固定，每次滑动一格即5s并计算该窗口内电压值的平均值将原始数据转换为 ( C1, C2,...,Cm)。计算公式如下：

其中m表示窗口的大小，xk表示窗口中每个电压值。得到降维后的数据 ( C1, C2,… ,Cm)，利用阳极换极后的特性即换极时电压下降至50 mv以下，平稳期电压为1500 mv左右这两个阈值分别判断换极开始时刻 tstart和电压恢复至平稳的时刻 tend，最后得到上升期长度。

（2）阳极压降速升/速降次数

阳极电压速升/速降是指在平稳期至下一次换极开始时这段时间内阳极电压由 V1陡然上升/下降至 V2之后，并能够保持上升/下降后的 V2值一段时间，这种情况就视作一次阳极压降的速升/速降。将该数据作为一维特征的目的是电解槽在生产过程中阳极压降会由于某些异常情况例如：阳极长包，偏流等导致电压出现波动，但经过处理后又保持稳定。通过统计速升/速降的次数来判断阳极全周期内电压整体波动情况。

（3）阳极压降速升/速降幅度

阳极压降速升/速降幅度是指阳极每次发生速升/速降情况时都会产生一定的电压差，统计这些压降差并计算相应的平均值就得到了速升/速降幅度。

（4）影响因子

影响因子是由日报数据中的针振和摆动所决定的。针振和摆动是描述电解槽槽电压是否平稳的两个物理量，当某些阳极在换极结束后，由于换极质量较差会导致电解槽中电压摆，使针振和摆动过大。影响因子的产生式如下：

2 阳极电压的k-means聚类分析

本文采用的数据集是4622号电解槽A，B两侧阳极压降的全周期数据，可以将数据集表示为C = { c1, c2,… ,cm}，而利用k-means聚类算法最终得到的簇集合为 D = { d1, d2,… ,dk}[10-12]。假设有样本X = ( x1, x2,… ,xn)，样本 Y = ( y1, y2,… , yn)，则样本X和Y之间的距离计算公式为：

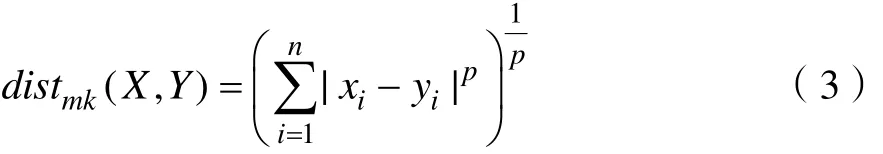
该距离度量方法是最常用的明可夫斯基距离（Minkowski distance），其中 1p≥ 。本文使用的是欧式距离即 2p= 。

k-means算法需要提前确定样本需要聚类的数目 k，本文利用了轮廓系数来评价在 k取不同值时k-means聚类的效果，轮廓系数的计算公式如下：

公式中aj表示在同一个簇中样本j到该簇中其他样本的距离的平均值，bj表示样本j到其它簇包含的样本的距离的平均值，在这些平均值中取最大值。K-means聚类算法所要达到的效果是同一簇内的样本之间越紧密越好即距离越小越好，不同簇之间样本的距离越大越好，这样聚类出来的效果比较好。

本文中利用k-means算法对阳极压降特征聚类过程如下：

1）输入数据集 C = {c1, c2,...,cm}， ci=（上升期长度，速升次数，速升平均幅度，速降次数，速降平均幅度，影响因子），以及k；

2）为了防止陷入局部最优情况，随机初始化k个中心 Oi；

3）计算数据集中每个样本 ci分别与这 k个中心 Oi的欧氏距离，将样本 ci归入到聚类最近的类别中去；

4）利用划分好的样本重新计算类中心，更新 Oi；

5）重复第3）和4）步，直到迭代的次数达到指定的最大值n或者是k个聚类中心值 Oi不再发生变化；

6）输出结果为簇集合 D = { d1, d2,… ,dk}；

3 实验结果及分析

本实验采用的数据是某铝厂4622号电解槽A，B两侧16个位置阳极压降数据，日期从2017年3月1日至2017年5月6日，每个位置取最后一次换极周期数据。并通过数据预处理得到每个位置阳极的完整周期数据，然后通过特征提取获取阳极换极后的上升期长度，阳极电压速升次数，速升平均幅度，速降次数，速降平均幅度，以及影响因子特征，对这6维数据进行聚类。

通过对6维特征进行聚类，聚类的个数分别取2，3，4，5，7，而轮廓系数的取值范围在[-1,1]，越接近于1聚类效果越好。如表1中可以看出当k=3时轮廓系数值最大，说明当类别确定为3时，电解槽阳极压降数据聚类效果最好，表明4622号电解槽中阳极压降波动的情况大致分为3类，而只需要观察这三类的波动情况就可以得出整个电解槽的电压稳定性情况。

表1 不同聚类类别k值下的轮廓系数对比Tab.1 Comparison of contour coefficients under different clustering category k values

本文通过对阳极压降的k-means聚类分析得出当k=3时效果较好。聚类结果如图2所示，相同形状的为一类，图中是类似于真实电解槽的示意图。

不同类别下阳极压降的波动情况如图 3，4，5所示，可以看出类别1的阳极换极之后上升期长度在45小时左右，说明电压很快回升至平稳，电解槽的针振和摆动幅度会相对较小；类别2的上升期为200小时左右，时间跨度很大因此会在很大程度上会影响整个电解槽的槽电压，也会较大程度上增大针振和摆动；类别 3中阳极换极之后电压变化较平稳，上升期为120小时左右。电解槽中每个阳极换极的质量好坏直接影响电压的波动情况从而导致整个电解槽的槽电压不平衡，增大能耗，影响生产效益。

4 结语

铝电解槽中阳极每次换极质量的好坏都会或多或少的影响整个槽的槽电压，槽电压过高或是过低一方面会增大能耗，减少电解槽的使用寿命[13]；另一方面会降低出铝量，进而影响生产效益[14-15]。通过对阳极压降原始分布数据进行预处理，得到阳极周期数据，并对阳极周期数据进行聚类划分，得到不同换极质量下阳极压降的波动状态。从而明确关键阳极，并有针对性地在换极过程中进行精细化作业，提高换极质量并对班组进行换极评价，考核，确保铝电解槽稳定生产。

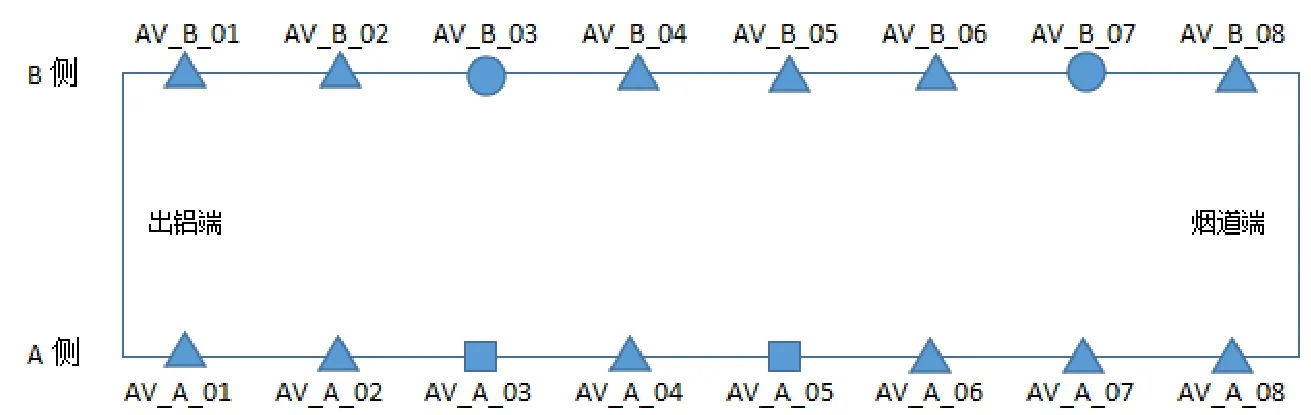
图2 聚类结果示意图Fig.2 Clustering results of the schematic

图3 类别1阳极压降波动曲线Fig.3 Category 1 anode voltage drop fluctuation curve

图4 类别2阳极压降波动曲线Fig.4 Category 2 anode voltage drop fluctuation curve

图5 类别3阳极压降波动曲线Fig.5 Category 3 anode voltage drop fluctuation curve

[1] 田庆红. 合理利用铝电解槽工作电压[J]. 轻金属, 2008.

[2] 田官官, 石良生. 浅析预焙阳极质量对铝电解生产的影响及应对措施[J]. 世界有色金属, 2014.

[3] 赵仁涛, 林立明, 张志芳等. 铝电解槽阳极数据分析[J].有色金属(冶炼部分), 2014.

[4] 刘永强, 李钊, 姬凤武等. 铝电解生产中阳极工作状态的分析[J]. 云南冶金, 2011.

[5] 肖瑞, 刘国华, 陈爱东, 宋转. 不确定时间序列统计降维方法[J]. 计算机科学, 2014.

[6] 谢福鼎, 李迎, 孙岩, 张永. 改进的符号化时间序列处理方法[J]. 计算机工程与设计, 2012.

[7] 余宇峰, 朱跃龙, 万定生等. 基于滑动窗口预测的水文时间序列异常检测[J]. 计算机应用, 2014, 34(5): 2217-2220,2226.

[8] 李峰, 肖建华. 在时间序列相似性问题中滑动窗口的确定[J]. 计算机应用, 2008.

[9] 翁小清, 沈钧毅. 基于滑动窗口的多变量时间序列异常数据的挖掘[J]. 计算机工程, 2007, 33(12): 102-104.

[10] Cao Ge, Cheng Yuhu.K-means Clustering Algorithm Based on Initial Clustering Centre Selection and Points Division[J].The Journal of New Industrialization, 2011, 1(5): 90-94. [曹戈, 程玉虎. 基于初始聚类中心选取和数据点划分的K均值聚类算法[J]. 新型工业化, 2011, 1(5): 90-94]

[11] XU Buyun, NI He.Comparative analysis of SOM and K-means clustering[J]. The Journal of New Industrialization,2014, 4(7): 63-65. [徐步云, 倪禾. 自组织神经网络和K-means 聚类算法的比较分析[J]. 新型工业化, 2014, 4(7):63-69]

[12] Zhang Xiaohua, Wang Le.Change detection based on multiscale and clustering[J]. The Journal of New Industrialization. 2011,1(3): 72-79. [张小华, 王乐. 一种多尺度和聚类分析的变化检测[J]. 新型工业化, 2011, 1(3): 72-79]

[13] 张报清, 雷霆, 余宇楠. 预焙槽阳极压降影响因素研究[J].矿冶,2015.

[14] 单淑秀. 我国电解铝工业的现状及发展方向[J]. 轻金属,2008(8): 3-6.

[15] 闫绍勇. 预焙阳极铝电解技术研发进展[J]. 轻金属, 2013.