光网络中若干路由和频谱分配算法研究

陈 鹏

（北京邮电大学，北京 海淀 100876）

0 引言

当前，以信息技术为核心的全球新一轮科技革命和产业变革正在蓬勃兴起，随着人们对网络带宽需求的快速增长，作为信息网络基础架构的核心一环，光网络具有不可替代的重要地位。弹性光网络的核心是路由和频谱分配问题研究，路由和频谱分配（RSA）问题是广泛研究的路由和波长分配（RWA）问题的一般推广，在光网络中，波长路由和波长分配是一个基础的研究问题，也是一个重要的研究课题。在路由和频谱分配问题中，频谱分配必须满足三个约束条件，相比路由和波长分配，增加了频谱连续性约束，这使得在路由和波长分配中研究的相应算法在路由和频谱分配问题不在适用，并且路由和频谱分配问题的研究会更加复杂。路由和频谱分配问题可以分为静态由和动态路由，也可以将路由和频谱分配问题拆分为路由问题和频谱分配两个子问题分析[1]。在近几年的研究中，有采用距离自适应调制模式[2,3]来分析路由和频谱分配问题，也运用智能算法优化路由选择机制和频谱分配[8,11,12]，负载均衡策略[14]和能量消耗[15]也被考虑到路由选择中，另外，路由和频谱分配问题也可以看作是多处理机调度[5]问题的一种特殊情况，因此，已经提出了几种调度算法分析求解固定选择路由和频谱分配问题中的资源使用情况。已知即使在简单的网络拓扑结构中，路由和频谱分配问题也是NP-难的，如在四个节点的线网络上频谱分配问题已经得到证实，在具有N个节点的环网络频谱分配研究存在一个3ε+近似算法[6]，另外，在星图上的频谱分配问题有一个4近似算法[7]。如何有效地分析的路由和频谱分配问题，是本文研究的主要目的。考虑到在网络拓扑结构中一条路由上分配的频谱必须是连续的，在动态路径建立和频谱资源释放过程中会产生一些频谱碎片[9,10]，降低了频谱使用效率[13]，如果能研究出很好的路由和频谱分配算法，既能节约光纤中带宽资源，还能保证业务通信质量[4]。为了节约频谱资源，考虑到图染色模型和路由和频谱分配问题之间的对应关系，我们从这个角度建立数学模型。优化网络拓扑结构上染色所要的染色数最少和满足请求所需的频谱资源数最少相对应，本文主要介绍了两者之间的模型转化和相关的算法分析，在以后的研究中这可应用到路由和频谱分配问题分析中。

1 模型转化

1.1 路由和频谱分配问题介绍

弹性光网中路由和频谱分配问题是光网络波分复用技术的路由和波长分配问题的一般推广和发展。路由和波长分配（RWA）问题是对于每一个业务连接请求通过选择一条合适的路线建立光路连接，并且沿着该路径分配合适的波长。在没有波长转换器的光网络中，在每个连接请求建立的端到端路径中必须分配相同的波长，这就是波长一致性约束条件。

定义1.1(RSA)：给定一个图 G = ( V, A)，其中V是顶点集，A是边集（有向边），和一个频谱需求矩阵 T = [ tsd]，其中 tsd表示请求从节点s到节点d需要的频谱数目，服务每一个业务请求寻找一条光路径和分配连续的频谱目标是使网络中所有请求使用的频谱总数目最少；

RSA问题约束条件：

（1）每一个请求分配连续的频谱资源；

（2）每一个请求在它路径的每条边上分配相同的频谱资源；

（3）使用同一条边的频谱分配的频谱段不相交；

如果每一个请求的路径给定，则RSA问题就退化为SA问题。

定义1.2（SA）：在约束从节点s到节点d的所有请求必须沿着给定的物理路径sdp 下RSA问题。

1.2 图染色模型

1.2.1 图染色模型介绍

定义 1.3（图染色）：经典图染色问题是在一个无向图G上，给G的每一个结点分配一种颜色，如果（ u, v）是一条边，表示两个节点相邻，则分配给u和v不同的颜色，目标是使用很少的颜色就能为G染色。形式化表示为，G的 k -染色是一个函数f: V → {1 ,2,… k }使得对每一条边（ u , v）有 f ( u)≠f( v)，其中1,2,…k表示可使用的颜色，函数f表示给每一个结点选择的颜色。如果G有一个 k -染色，则称它是 k -可染色的图。

定义 1.4（带权图染色：）带权图染色问题表示无向图G上的每一个结点v有一个权重 w ( v)，它表示给顶点v染色所需要的颜色数，与经典图染色问题最大不同之处在于经典图染色问题只需给每一个结点分配一种颜色，而带权图染色问题需要给每一个结点v分配 w ( v)颜色数。同时，有如果（ u , v）是一条边，则分配给u和v不同的颜色，目标是使用最少的颜色就能为G染色。

1.2.2 模型转化

考虑一般图 N = ( V, E)上的RSA问题，对于给定的请求集合 R = { ri| ri= ( si, ti, bi)}，业务请求 ri的路径给定，其中 bi表示请求 ri需要的频谱数。构造图G′= ( V′, E ′)的染色模型，（1）对于每一个结点v′∈ V ′，有请求集R中的一个请求 rv和节点v′相对应，即 v ′ ↔ rv= ( sv, tv, bv)；

（2）对于每一条边(u, v) ∈ E ′，当且仅当请求集R中的请求 ru和 rv有公共边，即 pu∩pv≠φ；

（3）对于图G′中每一个节点v′∈V所带的权值w( v′)，有请求集R中的一个请求 rv所需要的频谱数bv与之相对应，即 w ( v′) = bv；

RSA问题优化目标服务每一个业务请求使网络中所有请求使用的频谱总数目最少就转化为带权图G′定点染色使使用的颜色数目最小。

同时，满足下面的约束条件：频谱不相交约束，图G′中相邻两顶点使用不同的颜色数，为每个顶点v′∈V分配的色数区间为w( v′ ) = [ w, w + bv- 1 ]，即

频谱连续性约束，即分配给每一个顶点v′∈V上色数区间 w ( v′ ) = [ w, w + bv- 1 ]是连续的；

频谱一致性约束，即每一个顶点v′∈V染色使用的颜色是不同的；服务网络中所有请求使用的频谱总数目最少就等价于为带权图G′定点染色使使用的颜色数目最小。

2 设计算法

算法1：

输入：一个n个顶点的集合V， V ={vi| (w( vi))}

输出：顶点集V的染色数

开始时，所有顶点 vi未被染色，

对vi，1≤i≤n，

对区间图顶点度d(vi)按照降序排列，

即 d (v1) ≥ d ( v2)≥ … ≥ d ( vn)，

如果顶点 vi色数区间与已染色顶点色数区间不

相交，

依次按照首次适合方法为顶点 vi分配颜色，

结束

算法2：

输入：一个n个顶点的集合V，V ={vi| (w( vi))}

输出：顶点集V的染色数

开始时，所有顶点 vi未被染色，

对vi，1≤i≤n，

对区间图顶点度与权值积大小

{d(vi) × w( vi)}按照降序排列，即d(v1)× w( v1)≥d(v2) × w( v2)≥ … ≥d(vn) × w( vn)

如果顶点 vi色数区间与已染色顶点色数区间不相交，

依次按照首次适合方法为顶点 vi分配颜色，

结束

为了不失一般性，我们采用文献[6]中的网络拓扑图作为模型转化的对象，对于更加复杂的图同理按照上述算法分析。即将图1上的频谱分配问题转化图染色问题，其中图 1上请求为 r1= ( 2,3,3)，r2= ( 2,1,4)，r3= ( 1,4,2)，r4= ( 1,2,5)，r5= (1,4,2)，r6= ( 3,2,2)，按照上述算法(1)，转化为求为图2染色所需的染色数，其中图2表示每个节点所需要的色数。在满足图染色约束条件下图2所需染色数为7，考虑频谱分配问题有一个下界，可以认为不小于边 L1上所有请求需要的频谱总数，即所求染色数 7是频谱分配问题的最优解。

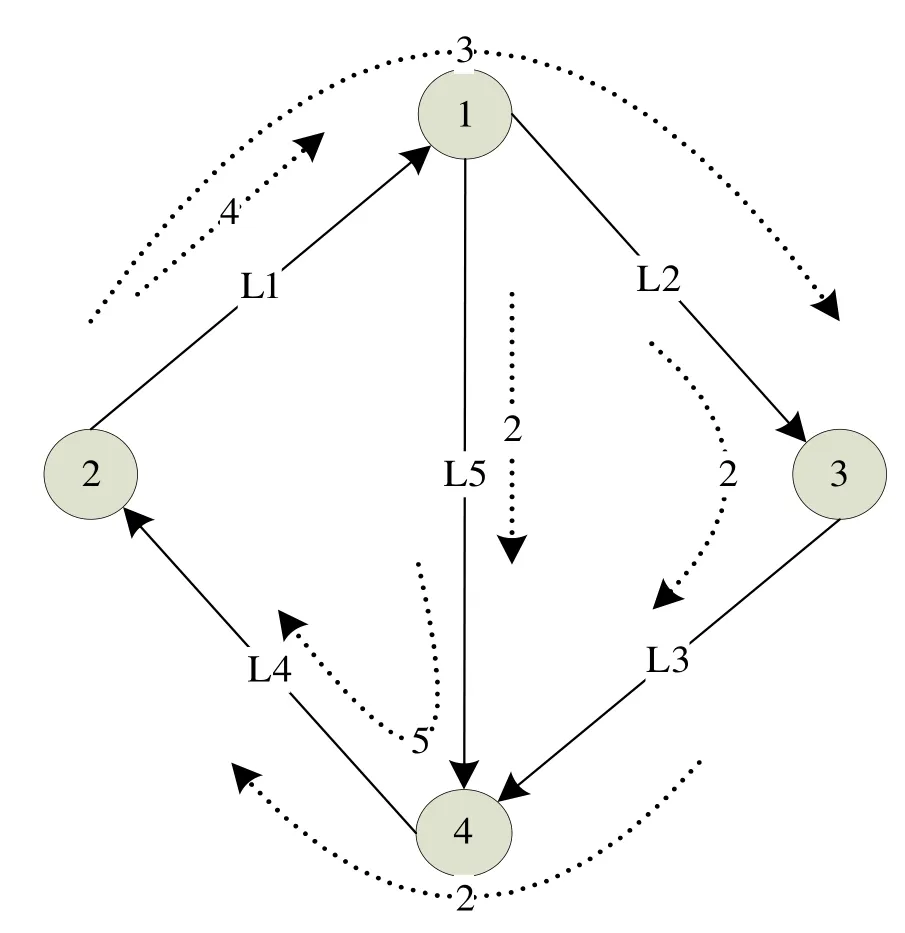
图1 具有五条有向边的网状网络上SA问题的实例Fig.1 Instance of the SA problem on a mesh network with five directed links

图2 对应最优图染色问题网络Fig.2 Optimal network of the corresponding graph coloring problem

3 总结

本文通过对网络中路由和频谱分配问题的研究，设计了图染色算法，并应用于路由和频谱分配问题中。在此过程中，首先介绍了路由和频谱分配问题，它是路由和波长分配问题的一般推广，为了模型的简化，证明了路由和频谱分配问题可以转化为图染色模型，并且图染色模型设计的算法也可应用于路由和频谱分配问题。本文主要介绍了模型转化及算法设计，以后还需对算法进行改进，完善算法。本文最后提出的算法，可以有效地求解路由和频谱分配问题，在以后研究可应用到弹性光网络路由和频谱分配问题分析中。

[1] BC Chatterjee , N Sarma , E Oki. Routing and Spectrum Allocation in Elastic Optical Networks: A Tutorial[J]. IEEE Communications Surveys & Tutorials, 2015, 17(3): 1776-1800.

[2] T Takagi, H Hasegawa, K Sato, Y Sone. Dynamic routing and frequency slot assignment for elastic optical path networks that adopt distance adaptive modulation[J]. Optical Fiber Communication Conference & Exposition, 2011,19(24): 1-3.

[3] S Talebi, I Katib, GN Rouskas. Distance-adaptive routing and spectrum assignment in rings[J]. Iet Networks, 2016,5(3): 64-70.

[4] Kewei Sha, Aaron Striegel, Min Song. Advances in Computer Communications and Networks: From Green,Mobile, Pervasive Networking to Big Data Computing[M].Netherlands: River Publishers, 2017.

[5] S Talebi, E Bampis, G Lucarelli, I Katib, GN Rouskas.Spectrum Assignment in Optical Networks: A Multiprocessor Scheduling Perspective[J]. IEEE/OSA Journal of Optical Communications & Networking, 2014, 6(8): 754-763.

[6] S Talebi , E Bampis , G Lucarelli , I Katib. On Routing and Spectrum Assignment in Rings[J]. Journal of Lightwave Technology, 2015, 33(1): 151-160.

[7] JC Bermond, FZ Moataz. On Spectrum Assignment in Elastic Optical Tree-Networks[J]. Inria Sophia Antipolis, Univ. Nice Sophia Antipolis, 2015.

[8] H Xuan, Y Wang, Z Xu, S Ha, X Wanga. New optimization model for routing and spectrum assignment with nodes insecurity[J]. Optics Communications, 2017, 389: 42-50.

[9] 赵永利, 张杰, 纪越峰. 频谱灵活光网络[M]. 北京: 人民邮电出版社, 2013.

[10] 鞠卫国. 灵活栅格光网络中的频谱碎片整理与动态路由算法. [D] 北京: 北京邮电大学, 2013.

[11] 李唱, 焦彦平. 一种基于改进蚁群的QoS单播路由算法[J].软件, 2013, 34(4): 42-45.

[12] 徐加利, 管章玉. 协作无线网络中基于遗传算法的联合中继选择与认知频谱接入机制[J]．新型工业化, 2014, 4(5):41-47.

[13] 孙健, 张锦南. 频谱资源利用评价体系研究[J]. 软件,2016, 37(02): 17-21.

[14] 冯伟, 别红霞. 具有拥塞感知w的Mesh 负载均衡路由策略[J]. 软件, 2013, 34(1): 56-59.

[15] 夏季文, 马福昌, 乔学工. 节能的无线传感器网络分簇路由算法的研究[J]. 新型工业化, 2011, 1(8): 56-63.