基于OpenMP的多核并行技术在电力系统工频电场计算中的应用

刘 哲，李永明，周 悦，邹岸新，徐禄文

（1. 重庆大学电气工程学院，重庆 400030；2. 国网重庆市电力公司电力科学研究院，重庆 401123）

0 引言

我国地缘辽阔，特高压输电能够实现大容量、远距离输电，降低损耗，节省线路走廊，有利于构建坚强电网[1]，正是高电压等级输电的这些优势，我国近些年发展建设了很多特高压线路。随着高压输电线路电压等级由超高压升高为特高压，特高压输电系统电压高、电流大，带电导体表面及附近空间的电场强度明显增大，电晕放电产生的可听噪声和无线电干扰影响突出[2]。输变电系统电磁场的工程计算是一项需要追求精度和时间的任务，为得到更为准确的结果，输电线路的仿真计算趋于三维化，同时考虑的环境因素也趋于复杂化，这些所带来的直接结果是所要计算的数据越来越多，给计算机带来了前所未有的挑战，所以怎样快速并又准确的计算出周围的电磁场分布一直是科研工作者追求的目标。

计算机技术日新月异，将计算机的技术优势最大限度地应用于电力系统，是目前国际智能电网的研究重点之一[3]。其中，计算机技术中的并行计算是解决大数据计算与时间复杂度之间矛盾的有效方法，也只有并行计算机可以解决今天日益增加的计算需要所面临的困难[4]。并行计算也不是什么新鲜事，在光化学，以及当下热门的云计算领域都有并行计算的身影[5]-[11]。并行计算就是可以同时对多个任务，多条指令进行处理，从而缩短计算时间提高计算的效率。目前并行计算主要有 2种方式，MPI和 OpenMP。MPI是通过多机群组合，并在机间通过消息传递的方式进行交流，达到并行计算的效果。但这种多机集群环境，内存不共享，在全局共享数据读写操作中，必须依靠机器间的通信来进行数据搬迁[12]，所以往往造成通信开销远远高于计算本身所花的时间。而多核环境中内存是共享的，可以省下通信开销，锁操作的效率远大于通信效率，并且在过去计算机的发展中，计算机都是单核高频的追求计算性能，但是在现有工艺下，改善 CPU 性能的传统方法如提升时钟速度和指令吞吐量等在摩尔定律限制下已经难有大的进展，单核发展已处于瓶颈状态，多核计算将成为未来的发展趋势[13]，所以过去的多台单核计算可以简化到现在一台多核计算机上，实现经济优化，编程优化等优势。

因此，本文采用可应用于单机多核的 OpenMP的并行计算方法，结合模拟电荷法研究特高压输电走廊的电场并行计算，仿真分析了离地1.5m工频电场的分布，对比串行算法验证其准确性，并分析并行计算在效率上的优势。

1 OpenMP 并行计算

OpenMP是一个为共享存储结构计算编写并行程序的接口，1997年10月，由SGI公司发起，HP、SUN、IBM和Intel等联合开发和推行一种新的共享主存编程模型的建议标准。其跨平台，可伸缩的模型给并行程序的设计者在桌面电脑和巨型机上开发并行程序提供了简单灵活的接口，在不降低性能的情况下克服了机器专用编译指示所带来的移植性问题，得到了各界的认可和接受[14]。编程模型以线程为基础[15]，主要应用于对称式共享存储器多处理机结构的并行计算机（SMP）。SMP是一类常见的共享存储并行计算机，其内部结构图如下1所示。

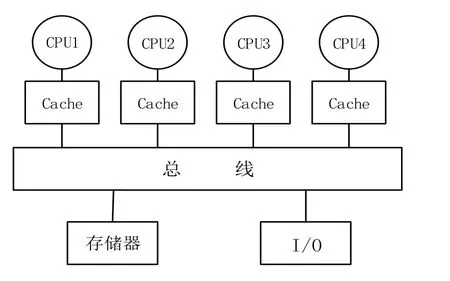
图1 SMP 结构图Fig.1 Structure chart of SMP

该类结构最重要的两个特点就是对称性和共享性，对称性是指系统中各个处理器的结构相同，地位相等，可以对称地访问存储器以及 I/O设备；共享性指的是存储器的地址共享，具有统一且唯一的地址空间，所有的处理器共享该地址空间。

OpenMP最基本的执行模式为fork/join并行执行模型，它编程简单并且可以增量开发。在OpenMP编程中，整个程序被看作一个大的串行执行结构，也可以叫做隐式初始任务区，并行结构只是其中的一个执行单元。并行结构中可以嵌套多个子并行结构，如果环境变量设置允许嵌套并行，这些嵌套子并行结构内还包含多个子孙并行结构。如图2所示，执行过程大致为，一个OpenMP程序从一个主线程开始，在程序某点需要并行时程序派生出一些额外的线程组成线程组，被派生出来的线程称为组的从属线程，并行区域中的代码在不同的线程中并行执行，当并行域中的代码执行完之后，其他并行线程销毁，控制流程回到单独的主线程来执行[16]。由于是共享内存的编程模型，降低了通信开销，用户不必处理迭代划分、数据共享、线程调度及同步等低级别的细节[17]。

图2 并行流程Fig.2 Parallel process

该模式的关键是判断数据间的依赖性，如果不存在依赖性，则可以直接插入#pragma omp parallel for 编译；如果存在依赖性，则需要对数据进行分析，查看是否可以通过循环变换或者分块等技术手段消除依赖性，或者进一步发现其内在的并行性。

2 模拟电荷法基本原理

CSM是基于电磁场的唯一性定理和等效原理，其原理简明，在具备场的基本概念的基础上，方法应用较为简捷，并可获得足够的计算精度[18]。其基本原理就是通过一组离散化的模拟电荷替代介质边界面上连续分布的束缚电荷，在已知电位的原边界面上设定与模拟电荷数目相当的匹配计算点，应用叠加原理建立各匹配点的电位方程，求解出各模拟点电荷值，并应用叠加原理得到场域中其他任意点的电位和电场值。

图3 单元线电荷Fig.3 Unit of line charge

图3 为单元线电荷计算示意图。将导线分为若干个有限长线段，每一线段用线性模拟电荷等效，设空间中有一直线段。

计算时，首先分段并对大地做镜像处理，求出各个匹配点产生的电位系数 P，再根据已知的边界条件建立如下矩阵方程：

pτφ= （1）

式中，p为输电线电位系数矩阵，τ为待求的线电荷列向量；φ为输电线匹配点电位列向量。

通过求解该方程，解出电荷的值，再根据电荷与电场之间的关系，计算出三个方向上的电场值Ex、Ey、Ez，然后再合成，求得空间中任意点P(x,y,z)产生的电场强度为：

3 并行计算

由于OpenMP比较方便的植入性，使原有的串行程序并行化，因此编程的时候首先编写输电线下建筑物周围电场计算的串行程序，然后再充分挖掘程序中可并行部分，对其进行并行程序编写，实现并行计算、提升计算的效率。

文中程序在装有 4核主频 3.30 GHz 的 Xeon CPU的服务器（内存8 G），Windows 10 64位系统上采用 C和 Matlab混合编写，C语言编译器Microsoft Visual Studio 2010版，在充分利用Matlab对于矩阵编写和计算的便利性的基础上，用VS2010编写 C语言并加入 OpenMP增加并行性，再用Matlab调用C语言所得数据画出仿真图形。

具体的，在Matlab中根据模型的坐标建立相应的矩阵，再通过mexFunction函数调用Matlab中矩阵的首地址把数据传入到C语言中，在C语言中进行并行程序的编写，在 Matlab用 mex语句调用 C语言中所得的结果绘出仿真图形。mexFunction函数的标准结构如下：

void mexFunction(int nlhs, mxArray *plhs[], int nrhs, const mxArray *prhs[])

{；//相应的语句}

其中整型参数nlhs[]和nrhs[]分别为输出参数个数和输入参数个数，mxArray类型参数plhs[]和prhs[]分别为输入参数的指针和输出参数的指针。

4 计算实例及仿真结果

4.1 计算模型

计算模型选取500 kV超高压输电走廊，每相采用4分裂导线，导线间距为0.323 m，子导线半径为0.0148 m；最低点离地14.19 m，档距为400 m，相间距为11.8 m。两个杆塔之间输电线的悬挂形状呈悬链线形状，当输电线两端的悬挂点对地高度一致时，由于对称性，弧垂的最大值则会出现在档距的中间点处。悬链线方程如下：

式中，σ0为导线水平应力，MPa；γ为导线比载，N/m·mm2；l档距，m；h导线最低点对地高度，m。

由于实际的超高压输电线路比较复杂，而有些因素的影响可以忽略不计，所以本文做如下简化：1、输电线表面等电位；2、地面是无穷大的导体，电位为零，沿线地面电阻率相同；3、认为电荷分布沿线路分布没有畸变，不考虑线路上电位的变化；4、只考虑线路主要部分形成的电场，忽略杆塔、金具、绝缘子等附近物体的影响。

简化后的模型如图 5所示，以输电线走向为 y轴，垂直输电线方向为x轴，垂直向上为z轴，坐标原点取在输电线中心位置。

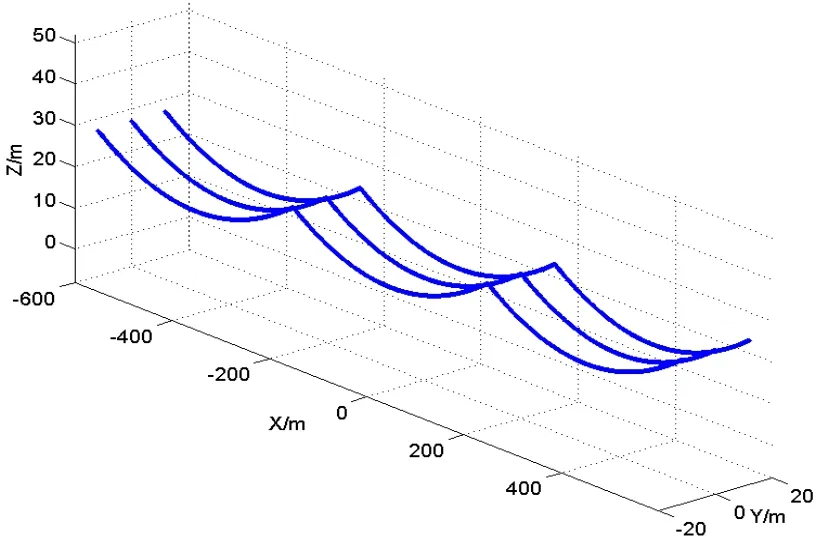
图5 输电走廊Fig.5 Pow er transmission corridor

4.2 计算精度

在精度方面，通过分别用Matlab和C语言并行编程计算，从量化的角度所得每一个点的电场结果作差比较，两值的差值最大也只能达到小数点后 6位；从可视化的角度，图6是取垂直于输电线路并通过建筑物的中心平面，通过叠加作图可以看到两个数值作出来的曲线几乎一模一样，两种角度证明了C语言并行计算下精度的可行性，并不会影响计算结果。

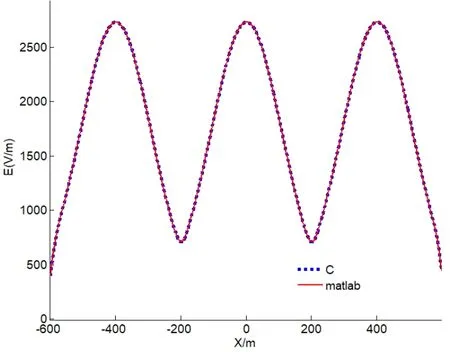
图6 C 语言和Matlab的结果对比Fig.6 Comparative results of C and Matlab

4.3 计算效率

仿真分析了输电走廊(x,y)=(-600~600，-20~20)，离地1.5 m工频电场的分布首先本次的模型在Matlab下计算时间为 36342 s，而 C语言单核串行下计算时间仅为186.79 s，仅从串行计算的角度，C语言就是Matlab计算速度的194倍。

并行计算中，加速比S(p)以及并行效率E(p)是评价并行效果的重要指标，其中S(p)是P个处理器同时计算求解时，单核串行时间与多核并行时间之间的比值，即

式中，Ts是单个处理器在串行模式下计算所花费的时间；TP是P个处理器在并行模式下计算所花费的时间。

并行效率E(p)是加速比与计算时所用到的CPU核数的比值，如式（5）所示。当加速比与核心数P接近时，并行效率越高。

描述这两个指标的重要定律：Amdahl定律。假设计算的问题固定规模不变，串行部分所占整个程序的比例f也不变，我们可以得到加速比S(p)为：

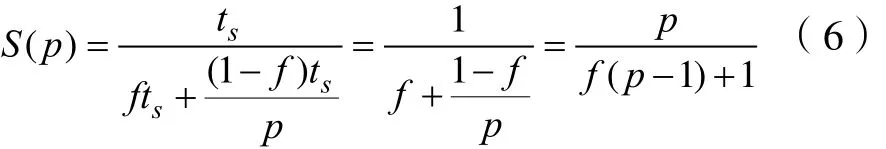
验证并行计算的有效性，并且为了避免计算的波动性，对每种情况都进行10次计算。

效果图如下所示：

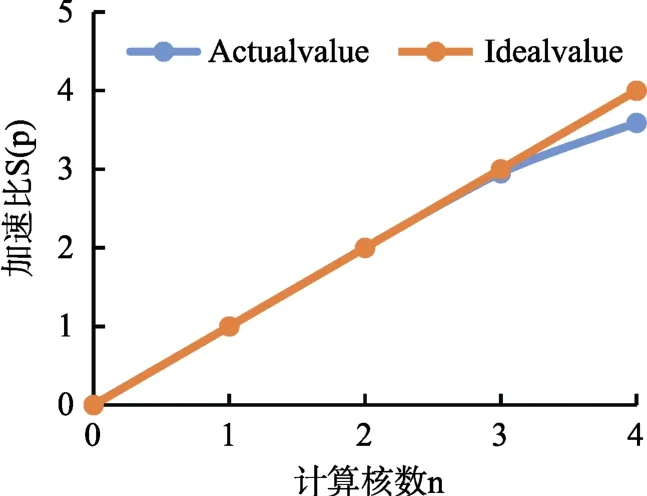
图7 加速比Fig.7 Accelerate rate

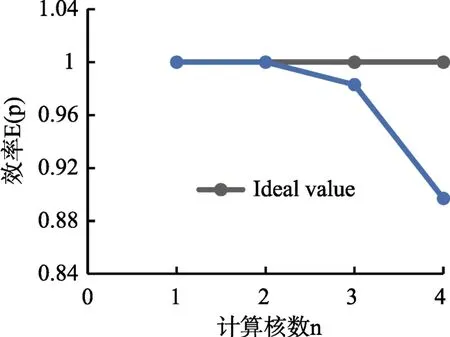
图8 加速效率Fig.8 Accelerate efficiency

双核模式下，加速比基本稳定在2.0，说明双核情况下并行起到了很好的加速效果；同样的模型在4核模式下，加速比为3.5以上，相比于4核情况下的理想结果有一点差距，原因之一是点电荷与线电荷计算的差异性，线电荷要进行较为复杂的积分运算，所以所花的时间相比点电荷较长，造成线程之间的等待；其次根据 Amdahl可知，串行占比也会对并行的效率造成影响。

5 结论

本文有别与传统的只采用Matlab进行编程的模式，引入C语言与Matlab混合编程，并在模拟电荷法的基础上引入OpenMP进行并行编程，既利用了Matlab生成矩阵的便捷性和对数据图像处理的强大功能，又利用了C语言的对于计算的快速编译性以及对于并行计算的可塑性，计算了500kV高压输电走廊下空间电场分布的情况，实现了对输电线走廊周围电场环境的快速求解，为其他类似电磁场数值计算提供了思路。

[1] 王艳, 王树欢, 等. 特高压六相输电线路工频电场强度计算[J]. 中国电力, 2015, 48(3): 44-49.WANG Y, WANG S H, et al. Calculation of Power Frequency Electric Field Intensity of UHV Six-phase Transmission Lines[J]. ELECTRIC POWER, 2015, 48(3): 44-49.

[2] 刘振亚. 中国特高压交流输电技术创新[J]. 电网技术,2013, 37(3): T1-T8.LIU Z Y. Innovation of UHVAC Transmission Technology in China[J]. Power System Technology, 2013, 37(3): T1-T8.

[3] 梅生伟, 朱建全. 智能电网中的若干数学与控制科学问题及其展望[J]. 自动化学报, 2013, 39(2): 119-131.MEI S W, ZHU J Q. Mathematical and Control Scientiflc Issues of Smart Grid and Its Prospects[J]. ACTA AUTOMATICA SINICA, 2013, 39(2): 119-131.

[4] B. Butrylo, F. Musy, L. Nicolas. A survey of parallel solvers for the finite element method in computational electromagnetics[J]. 2004, COMPEL Vol. 23 Iss 2pp. 531-546.

[5] 赵忠献, 李鸿健, 豆育生. 并行矩阵乘的光化学反应模拟研究[J]. 软件, 2010, 31(10): 16-20.ZHAO Z X, LI H J, DOU Y S. Research on parallel matrix multiplication Simulation of Photochemical Reactions[J].Software, 2010, 31(10): 16-20.

[6] 刘静. 基于独立生成树的网络多路径传输方法研究[J]. 软件, 2016, 37(4): 25-28.LIU J. Research on the Multi-path Transmission Method Based on Independent Spanning Tree[J]. Software, 2016,37(4): 25-28.

[7] 刘成军. 基于消息传递接口的线性方程组并行计算研究[J].软件, 2013, 34(1): 119-120.

[8] 唐万和, 杨海东, 黎展滔, 等. 考虑能耗成本和拖期成本的非同等并行机调度[J]. 软件, 2014, 35(3): 52-57.

[9] 曾晋, 吕韬. 一种基于零系数检查的通道并行算法[J]. 软件, 2014, 35(4): 153-156.

[10] 唐曼. 无线环境下基于多流优先级的并行多路传输[J]. 软件, 2014, 35(10): 46-50.

[11] 武涛. 基于云计算的并行动态路径搜索算法研究[J]. 软件,2015, 36(4): 128-132.WU T. Research on Parallel Dynamic Path Search Algorithm Based on Cloud Computing[J]. Software, 2015, 36(4): 128-132.

[12] T. Oyama, T. Kitahara, Y. Serizawa. Parallel processing for power system analysis using band matrix[J]. IEEE TRANSACTION ON POWER SYSTEMS, 1990 Vol. 5 NO. 3 1010-1016.

[13] 周伟明. 多核计算与程序设计[M]. 武汉: 华中科技大学出版社, 2009.ZHOU W M. Multi-core Computing and Programming[M].Wuhan, China, Huazhong University of Science and Technology Press, 2009.

[14] The OpenMP API specification for parallel programming[EB/OL]. http://www.openmp. org/wp-content/uploads/openmp-4.5.pdf.2016.11.

[15] Leonardo D, Ramesh M. OpenMP: An Industry Standard API for Shared-Memory Programming[J]. IEEE Computational Science and Engineering, 1998, 5(1): 46-55.

[16] 邹竞, 马华. 一种基于OpenMP的并行混合PVS算法[J]. 计算机应用研究, 2016, 33(1): 56-59, 91.ZOU J, MA H. Parallel hybrid PVS algorithm based on OpenMP[J]. Application Research of Computers, 2016, 33(1):56-59, 91.

[17] Q uinn M J. Parallel programming in C with MPI and OpenMP[M]. 北京. 清华大学出版社, 2005.

[18] 倪光正, 钱秀英. 电磁场数值计算(第2版)[M]. 北京: 机械工业出版社, 2010. 1.