光伏发电系统光伏并网逆变器控制策略研究
2018-04-20潘晓贝
潘晓贝
(1.河南省高校节能照明工程技术研究中心,河南三门峡472000;2.三门峡职业技术学院电气工程学院,河南三门峡472000)
太阳能由于其清洁无污染、可再生等诸多优点被全世界广泛关注。光伏发电能够节能减排、降低能耗,是目前电力专家认为最重要的新能源模式之一。对于光伏发电并网系统而言,整个系统最为关键的技术就是并网逆变器的实现,即控制策略的实现。逆变器控制策略的基本原理为:首先根据电网电压矢量和逆变要求的有功功率和无功功率算出电流矢量,再得到电压矢量指令,最后通过正弦脉宽调制技术使逆变器交流侧按指令输出所需电压矢量[1]。这种间接电流控制的缺点是:对系统参数变化较为敏感;动态响应速度慢;无电流反馈控制,输出电流波形品质不易保证。
针对以上的不足之处,本文提出了直接电流控制方案,即基于电流闭环的矢量控制策略。也就是对电网电压矢量定向,通过直接电流控制逆变器输出的有功功率和无功功率。这种方法称为基于电压定向的直接功率控制(V-DPC)。
1 直接功率控制
直接功率控制的原理是:并网逆变器输出瞬时有功功率和无功功率,先对瞬时有功功率和无功功率进行检测、运算,再把运算得到的瞬时功率的偏差值送到相应滞环比较器,最后分析滞环比较器的输出和电网电压矢量位置,从而得到驱动功率开关管的状态。直接功率控制需要计算瞬时功率,下面阐述瞬时功率的定义并分析不同坐标系下的瞬时功率的计算方法。
1.1 各坐标系下瞬时功率的计算
1.1.1 瞬时功率的定义
三相电中,相电压矢量Uabc的瞬时值是Uabc=[uaubuc];相电流矢量Iabc的瞬时值是Iabc=[iaibic]。
当电压矢量Uabc定向,ip(有功电流分量)和iq(无功电流分量)由电流矢量Iabc分解而得。ip与电压矢量同向,iq与电压矢量垂直。模
瞬时有功功率p、瞬时无功功率q分别为
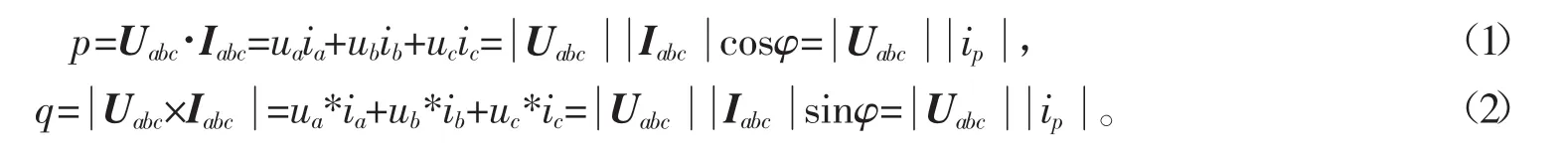
另外根据瞬时功率因数可以定义为λ=cosφ,显然

1.1.2 三相静止abc坐标系下瞬时功率的计算
由式(1)~(3)可得瞬时有功功率和瞬时无功功率为

其中,ua*、ub*、uc* 满足

显然瞬时无功功率也可以由三相静止坐标系下的无功功率Qabc得到,即
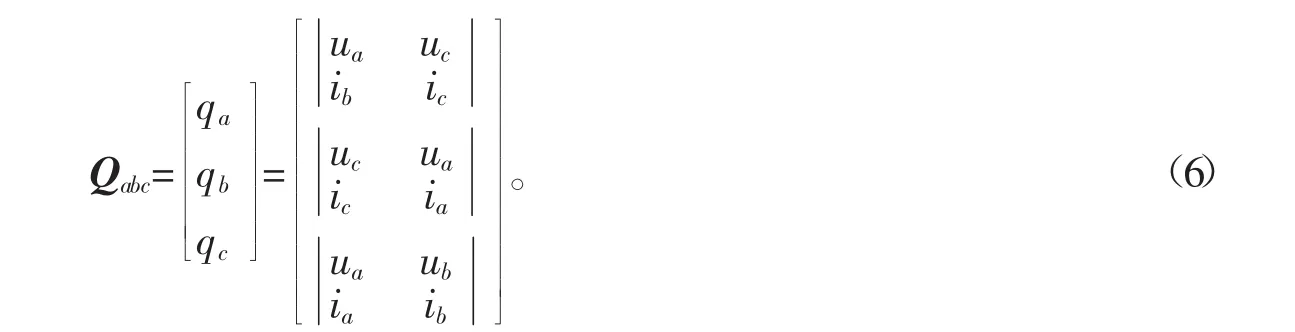
此时,可得瞬时无功功率q为

另外,复平面上的复功率S的实部为瞬时有功功率,虚部为瞬时无功功率。复功率S为
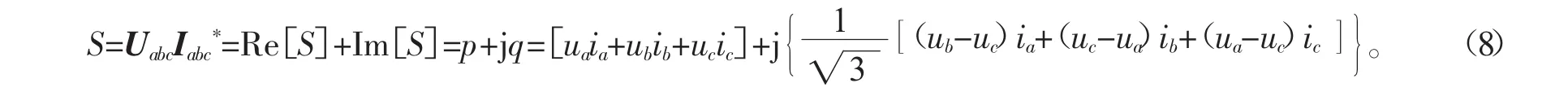
1.1.3 两相静止αβ坐标系下瞬时功率的计算
当三相静止abc坐标系变为两相静止αβ坐标系时,设Tabc/αβ是等功率变换矩阵,则
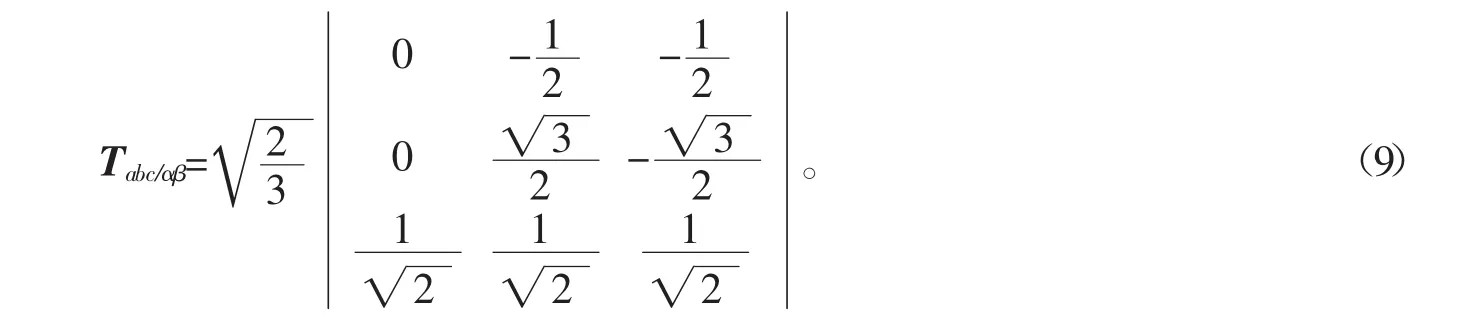
经变换矩阵变换得到两相αβ坐标系中的电压、电流矢量为

其中,i0、u0分别为零序电流分量和相电压零序分量。
此时,两相αβ坐标系下的瞬时有功功率p为

同理,瞬时无功功率也可由两相静止αβ坐标下的无功矢量Qαβ表示为

其中,K为单位矢量,垂直于αβ坐标系。
显然,瞬时无功功率q为Qαβ的模值比较式(11)可以得到两相αβ坐标系下的瞬时无功功率q为

可用矩阵形式表示瞬时功率,即

1.1.4 两相旋转dq坐标系下瞬时功率计算
当三相静止abc坐标系变为两相同步旋转dq轴坐标系时,设Tabc/dq是变换矩阵,则
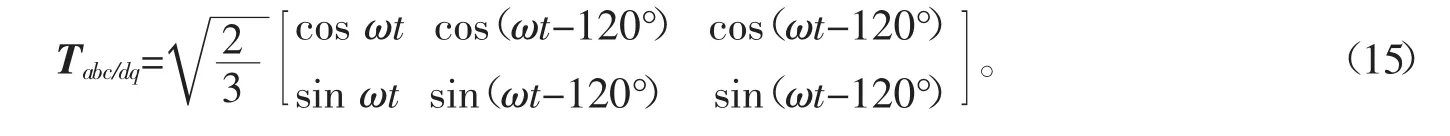
经变换矩阵变换可得到两相静止dq坐标系下Udq和Idq表达式为

结合瞬时有功功率的概念与瞬时无功功率的概念,两相静止dq坐标系下的和的表达式分别为
1.2 基于电压定向的直接功率控制

1.2.1 并网逆变器直接功率控制中瞬时功率的计算
1.2.1.1 有电网电压传感器时
有电网电压传感器时计算瞬时功率,要用电网电压矢量E取代前面瞬时功率表达式中的电压矢量U[2]。采用电网电压传感器检测电网电压,通过Tabc/dq变换把检测到的三相电压ea、eb、ec和三相电流ia、ib、ic变换为两相静止 αβ 坐标系下的 eα、eβ和 iα、iβ。再由式(11)和(13)计算得到相应的瞬时有功功率和无功功率。
1.2.1.2 无电网电压传感器时
在并网逆变器的控制中,所用到的交流电流传感器和直流电压传感器必不可少,而电网电压传感器有时可以省略。无电网电压传感器的系统电压值无法测量,只能通过一定的方法对电网的电压值进行估计。具体方法如下所述。
(1)瞬时无功功率的计算
由式(8)可得到并网逆变器的瞬时复功率表达式为
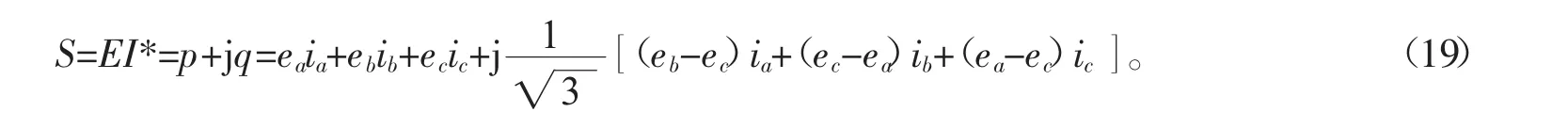
式(19)中,并网输出电流的瞬时值 ia、ib、ic是可由电流传感器检测得到,但电网电压的瞬时值 ea、eb、ec为未知量,只能通过估算方法得到。具体方法为:1)用传感器检测出的输出电流和直流侧电压值;2)计算出瞬时有功功率、瞬时无功功率的估算值;3)计算出电网电压的估计值,利用电压方程来计算[3]。于是,根据式(19)可得出瞬时无功功率q为

其中,ebc=eb-ec。
(2)瞬时有功功率和无功功率的估算
设Sa、Sb、Sc为a、b、c各相的开关函数,即并网逆变器开关调制时。这里,当逆变器的上3个桥臂开关管导通时,令Sx(x=a、b、c)=1;当逆变器的下3个桥臂开关管导通时,令Sx(x=a、b、c)=0[4]。此时忽略并网逆变器输出回路中电阻的影响,由此得出并网逆变器的电网电压表达式为

对应的线电压形式为
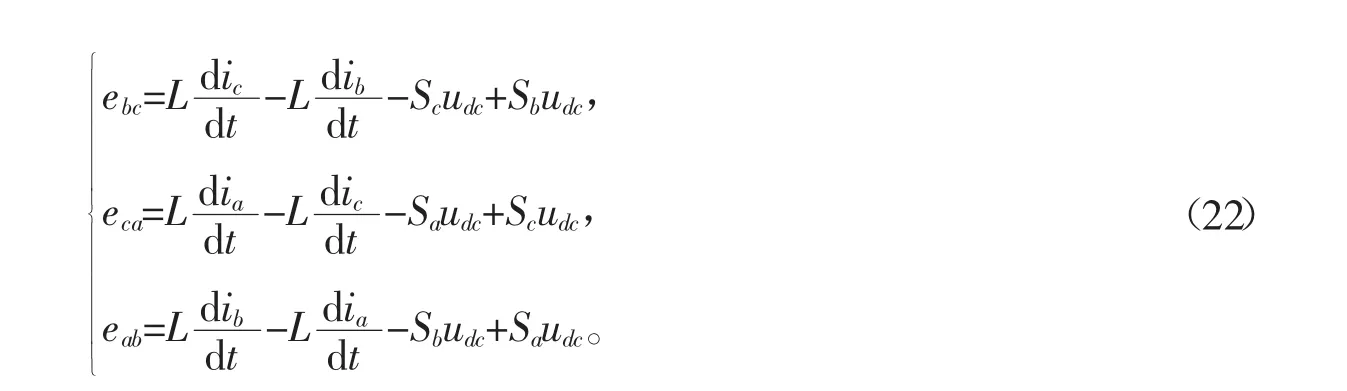
联立式(21)和(19),可得瞬时有功和无功功率的估算值分别为
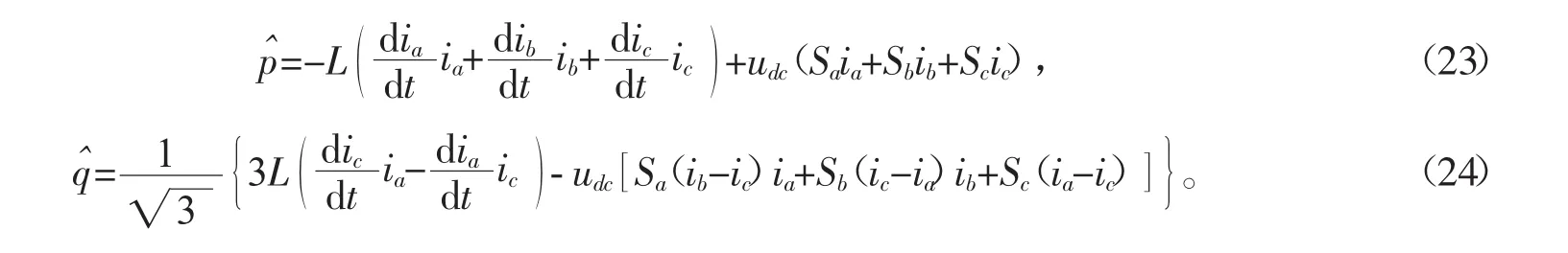
(3)电网电压矢量估算


变换式(26)则得到

1.2.2 无电网电压传感器的电压定向直接功率控制(V-DPC)
无电网电压传感器的直接功率控制系统结构如图1所示。其基本原理为:由开关函数(Sa、Sb、Sc)、输出电流(ia、ib)和直流侧电压 udc,经过式(23)、(24)及(27)计算得到瞬时有功、无功功率的估算值pˆ、qˆ和三相电网电压在αβ坐标系的估计值比较瞬时有功、无功功率的估算值和参考值,将比较结果送到滞环比较器,从而得Sp、Sq信号。p*由外环调节器输出给定,q*由系统的无功指令给定,若使并网逆变器单位功率因数运行,则q*=0;最后得到用来驱动逆变器的开关管调制,即输出电压的开关函数(Sa、Sb、Sc),并把开关状态信号反馈到功率和电压单元进行估算[5]。
在图1所示的V-DPC结构中,控制的关键之处在于:将瞬时功率的参考值与估算值进行比较,将比较结果送到滞环比较器,根据滞环比较器输出值并结合电压矢量的位置,对应开关表,各个逆变器的开关状态就得出了。
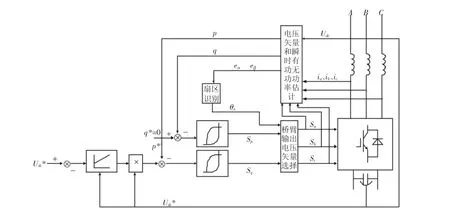
图1 控制系统结构
1.3 功率滞环比较器
DPC控制器的关键是功率滞环比较器。在无电网电压传感器的V-DPC系统中,功率滞环比较器的输入信号是瞬时有功功率参考值与估算值的差值和瞬时无功功率参考值与估算值的差值Δq,Sp和Sq是其输出信号,Sp和Sq反映的是功率的偏离程度。图2为功率滞环比较器的滞环特性,分别是有功功率滞环比较器滞环特性和无功功率滞环比较器滞环特性。
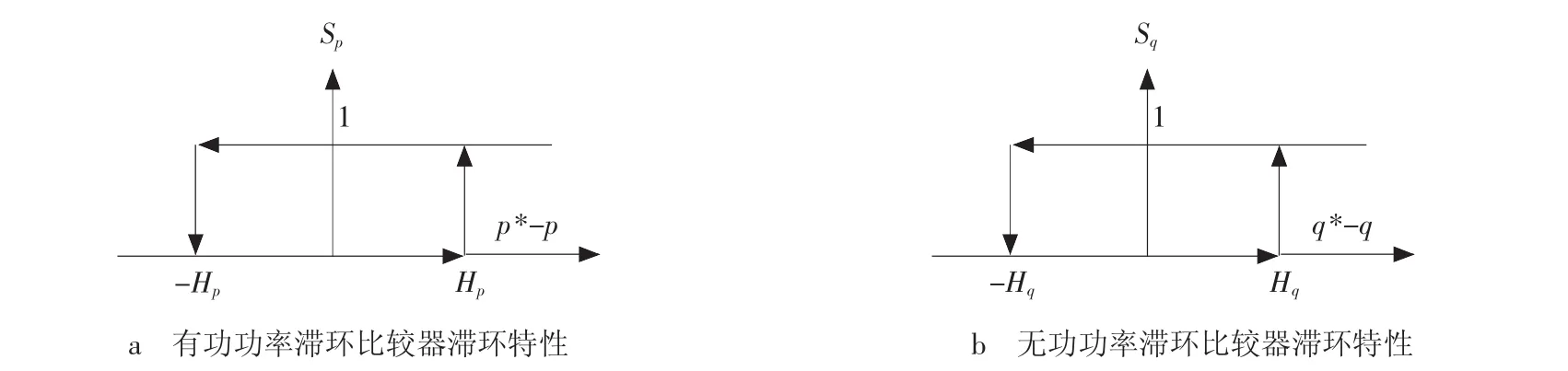
图2 滞环比较器滞环特性
滞环比较器的比较结果分别如下

图2中,Sp和Sq只有0或1两种状态。Δp=p*-p,Δq=q*-q;2Hp和2Hq分别为有功功率和无功功率滞环比较器的滞环宽度。
因此,只有在滞环宽度小于瞬时功率偏差的绝对值时,开关状态才发生改变。开关状态的每次改变,都可以使偏差量减小。
1.4 开关状态表
如图3所示,逆变器的电压空间矢量由U1~U6这6个非零矢量和U0、U7这2个零矢量共8个矢量组成。电压矢量由Sa、Sb、Sc和udc决定。SaSbSc=000~111,分别对应于U0(000)、U1(001)、U2(010)、U3(011)、U4(100)、U5(101)、U6(110)、U7(111)共8个电压矢量。矢量扇区可以用来表示电网电压矢量区域位置,结合电网电压矢量区域位置和滞环比较器的输出结果可以得到开关状态。
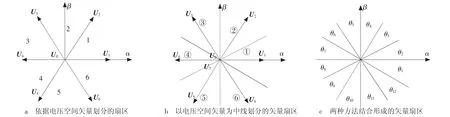
图3 矢量扇区的划分
1.4.1 扇区矢量的划分
1.4.1.1 依据电压空间矢量划分的1~6的扇区
通过电压型逆变器的输出6个非零电压空间矢量将αβ平面分成6个独立的矢量扇区,如图3a所示。这种划分形成了一个正六边形,分别由6个非零电压矢量和两个零电压矢量组成。这种扇区划分方法在空间矢量的调节中得到了广泛的应用,并可以通过参考电压矢量所在扇区的两个相邻的非零电压矢量和一个零电压失量的合成来实现参考电压矢量的跟踪控制。但是,在直接功率控制中瞬时功率的滞环比较代替了参考电压矢量的跟踪控制,因而空间矢量调制的方法不能直接用于调节瞬时功率。但是,通过改变开关函数,这种扇区的划分仍然可以用于瞬时功率的跟踪控制,而通过控制并网逆变器输出电压的幅值和相位就可以达到调节逆变器输出功率的目的。
1.4.1.2 以电压空间矢量为中线划分的1~6矢量扇区
以电压逆变器的6个非零电压矢量作为中线,将αβ平面分成滞后第一种矢量扇区30°的6个矢量扇区,如图3b所示。这种扇区θ的划分同样可以实现瞬时功率的跟踪控制。
1.4.1.3 以上两种方法结合形成的矢量扇区
将上述两种划分的矢量扇区重叠,从而将αβ平面划分成矢量扇区为θ1~θ12,如图3c所示。这些矢量扇区θ的取值范围为
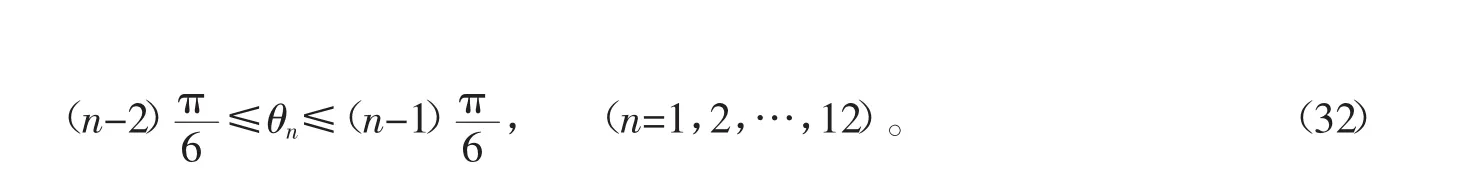
矢量 E 的相角根据 eα、eβ得到矢量E所在的矢量扇区由前面相角范围计算来确定。例如说明电压空间矢量 E 在 θ1扇区内。
1.4.2 开关状态表的确定
瞬时功率受到并网逆变器中8个电压矢量U0~U7的影响大小是不相同的,需要选择合适的电压矢量来调节输出瞬时功率。开关状态表即DPC控制所需要的开关状态Sa、Sb、Sc,它是结合滞环比较器的输出结果和电网电压矢量的位置得到的[6]。得到了开关状态表,逆变器桥臂所需的输出电压矢量Ur就得到了。开关状态表如表1所示。
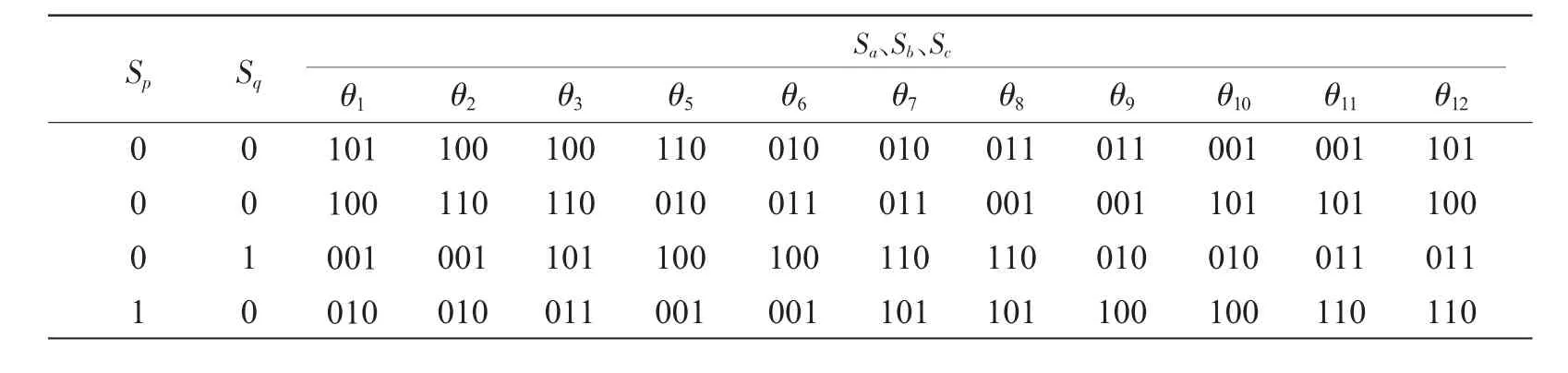
表1 开关状态表
2 仿真研究
系统仿真模型利用MATLAB软件中的SIMULINK组件构建。参数为直流电压400 V,输出功率10 kW,交流侧电感1 mH,直流侧电容1 mF。有功功率动态响应仿真波形如图4所示,无功功率动态响应仿真波形如图5。
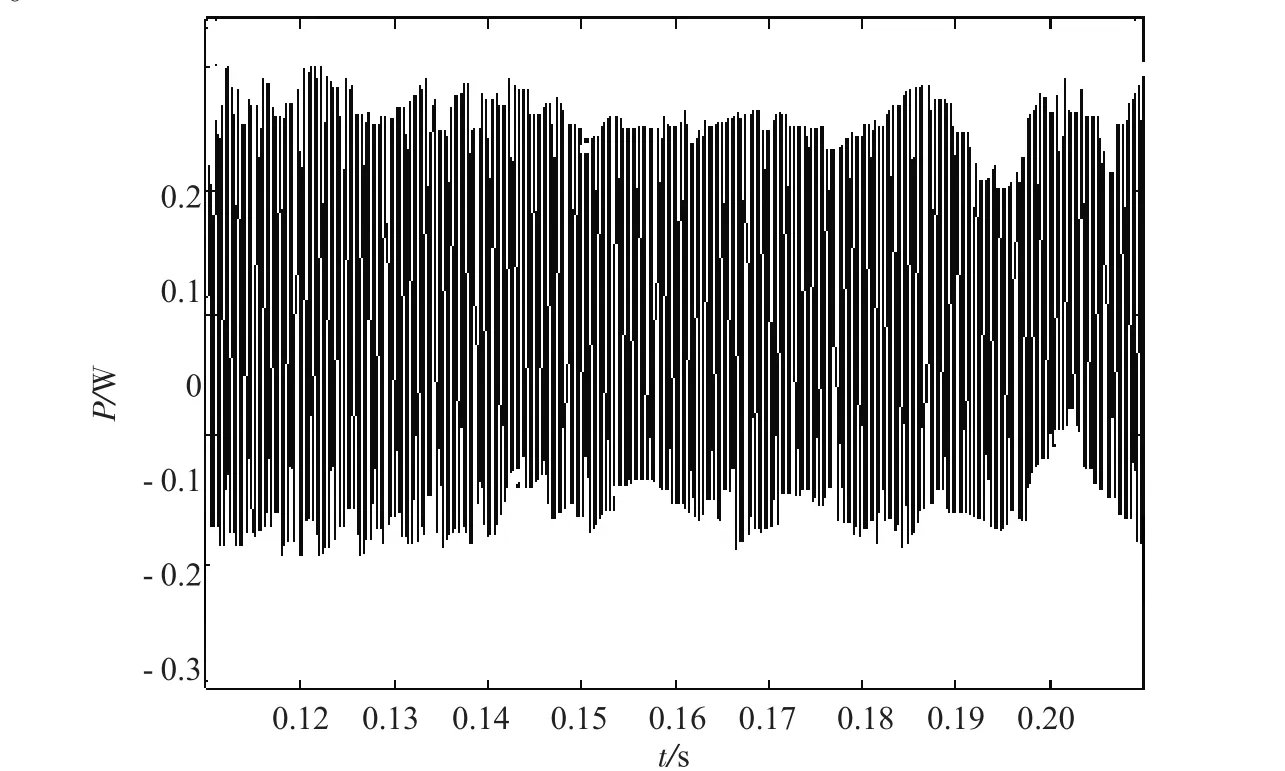
图4 无功功率动态响应仿真波形
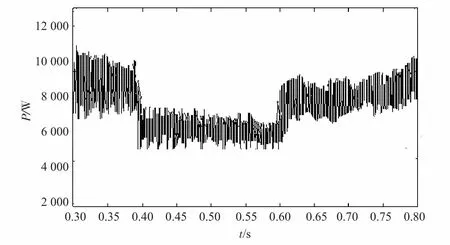
图5 有功功率动态响应仿真波形
观察图4和图5可得出,无功功率接近于零,有功功率响应迅速,短时间内就能到达给定值。图5中,在0.38 s至0.63 s有功功率有一个瞬降以平衡并网功率,这是因为回馈功率变化引起母线电压瞬降从而引起的[7]。
图6为逆变器输出电流和电网电压波形。由图6可以看出,无电网电压传感器时,在电压定向直接功率控制下,光伏逆变器输出电流与电网电压频率相同、相位相同。
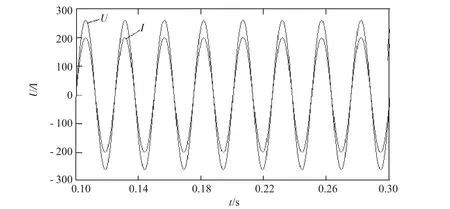
图6 逆变器输出电流和电网电压波形
3 小结
本文对并网控制策略进行了重点研究,提出无电网电压传感器的电压定向直接功率控制策略,该控制策略与其他控制策略相比,能使系统运行更稳定[8]。从仿真的输出图像来看,采用该控制策略,系统输出的电流与电网电压频率和相位均相同,从而保证整个并网控制运行。
参考文献:
[1]柴文野.三相光伏发电并网系统及其控制方法的研究[D].淮南:安徽理工大学,2012:21-49.
[2]张兴,曹仁贤.太阳能光伏并网发电及其逆变控制[M].北京:机械工业出版社,2010:70-83.
[3]张胜权.三相光伏并网逆变器控制策略研究[D].哈尔滨:哈尔滨工程大学,2012:47-61.
[4]柴文野,祝龙记.基于电压定向直接功率控制的光伏并网逆变器[J].电源技术,2012,4(36):527-570.
[5]尚磊,孙丹,胡家兵,等.三相电压型并网逆变器滑模变结构直接功率控制[J].电力系统自动化,2010,34(14):79-83.
[6]陈树勇,鲍海,吴春洋,等.分布式光伏发电并网功率直接控制方法[J].中国电机工程学报,2011,31(10):6-11.
[7]陈道炼.DC-AC逆变技术及其应用[M].北京:机械工业出版社,2003:11.
[8]郭小强,乌仔伟扬,顾和荣,等.并网逆变器LCL接口直接输出电流控制建模及稳定性分析[J].电工技术学报,2010,25(3):102-109.
