三维场景的光场成像仿真*

刘严羊硕， 潘晋孝， 潘毅华， 刘　宾

(1. 中北大学 理学院， 山西 太原 030051； 2. 中北大学 电子测试技术国家重点实验室， 山西 太原 030051； 3. 中北大学 信息探测与处理山西省重点实验室， 山西 太原 030051)

Gershun在1936年提出光场的概念， 定义其为光辐射在空间各个位置向各个方向的传播[1]. 之后， 光场理论又得到了不同程度的改进. 直至1996年Levoy提出光场渲染理论(light field rendering, LFR)利用四维光场函数来描述光场， 并通过两个相互平行的平面对四维光场进行参数化表示， 光场理论才得到了完善[2]. 光场信息在实现重聚焦， 深度估计及光谱成像等方面都有广泛的应用[3-7].

目前获取光场信息的方式主要有微透镜阵列、 相机阵列及掩膜方式. 微透镜阵列方式是将微透镜阵列放置于一次像面处， 探测器平行于微透镜阵列放置于微透镜阵列焦距处， 利用探测器记录位置信息， 利用微透镜阵列记录方向信息来获取四维光场信息[8-10]. 相机阵列是通过在空间排布多个相机得到一系列不同视角图片的光场获取方式[11-14]. 掩膜光场成像模型是在透镜及探测器之间放置一片拥有特殊编码的掩膜， 通过这种不同位置透视率不同的掩膜来对入射光进行强度调制[15]. 这3种方式较为常用的是微透镜阵列方式及相机阵列方式. 虽然相机阵列相比于微透镜阵列可以拍摄更为丰富的角度， 处理上也更为直观简便， 但是微透镜阵列质量轻， 体积小， 造价低廉且利于集成化， 例如Lytro在内的很多手持光场相机均是利用微透镜阵列制造而成[16].

为了光场成像算法研究获取第一手数据， 减小硬件投资造成的成本问题， 同时可以灵活改变系统参数， 指导系统设计， 本文提出了一种基于微透镜阵列的光场相机仿真方法. 该方法以Levoy的光场渲染理论为基础， 通过将二维图像以金字塔方式逐层向后推移扩展有效面来设置不同物距的图像， 再通过光路追迹及遮挡判断计算每一物点对应在探测器上的位置坐标， 得到光场图像.

1　光场成像基本原理

1.1　微透镜阵列光场采样原理

传统成像方式所成的像仅能反映出光的强度及位置信息， 而不能反映出光的方向信息， 这是因为每一个像元上所获得的光线能量均是来源于所有方向的光能量叠加而成， 这一成像过程中损失了光线的方向信息.

与传统成像方式不同， 将微透镜阵列放置于主透镜像面处， 将探测器放置于微透镜后记录来自不同方向的光. 根据光场采样理论， 探测器所接收到的光是四维光场的重采样， 能够记录光线的方向信息， 如图 1 所示， 单个微透镜接收来自主透镜所有方向的光在探测器上形成一个宏像素. 宏像素下包含很多像元， 每一个像元对应于主透镜分块后的一个子孔径， 经过不同的子孔径入射来的光代表不同的方向， 一个宏像素下的不同像元记录了来自不同子孔径的光， 相当于记录了光线的方向信息.

对于单个子孔径来说， 物体经同一子孔径打在微透镜阵列的光会在其对应宏像素的相同位置处成像， 如图 2 所示. 利用这一规律， 给光场图像的解码提供了理论依据， 解码相当于将每一子孔径所成的像展示出来. 子孔径相当于光圈减小后的主透镜， 其景深增加， 但信噪比降低.

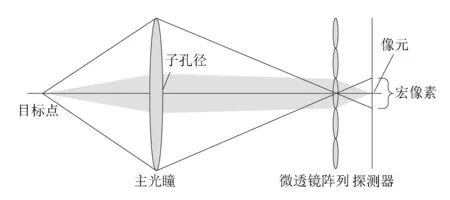
图 1　基于微透镜阵列的光场采样Fig.1　Light field sampling based on microlens array

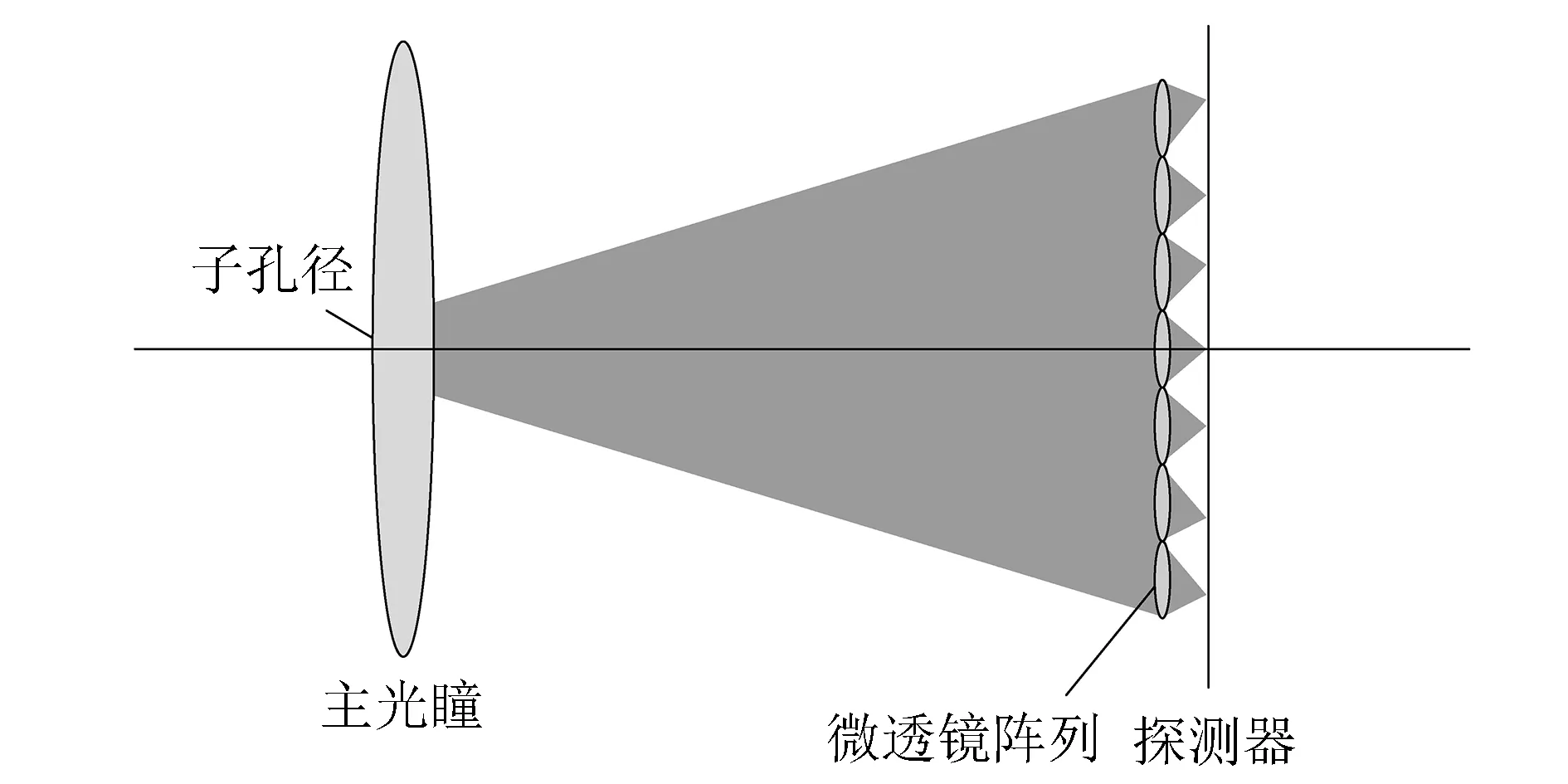
图 2　单个子孔径成像光路Fig.2　Optical path of single sub-aperture imaging

每一个宏像素与一个微透镜的大小近似相等， 由图2可知， 一个宏像素下的像元个数决定主透镜所分的子孔径块数， 而子孔径块数决定可以分辨光场的方向数. 因此一个宏像素下的像元个数决定方向分辨率， 而微透镜的个数决定空间分辨率.

1.2　数字重聚焦

由于所采集到的光场为多个物距上平面组成的三维场景， 故需要对其进行数字对焦. 数字对焦就是将所采集到的光场重新投影到新的像平面进行积分. 重聚焦示意图如图 3 所示.

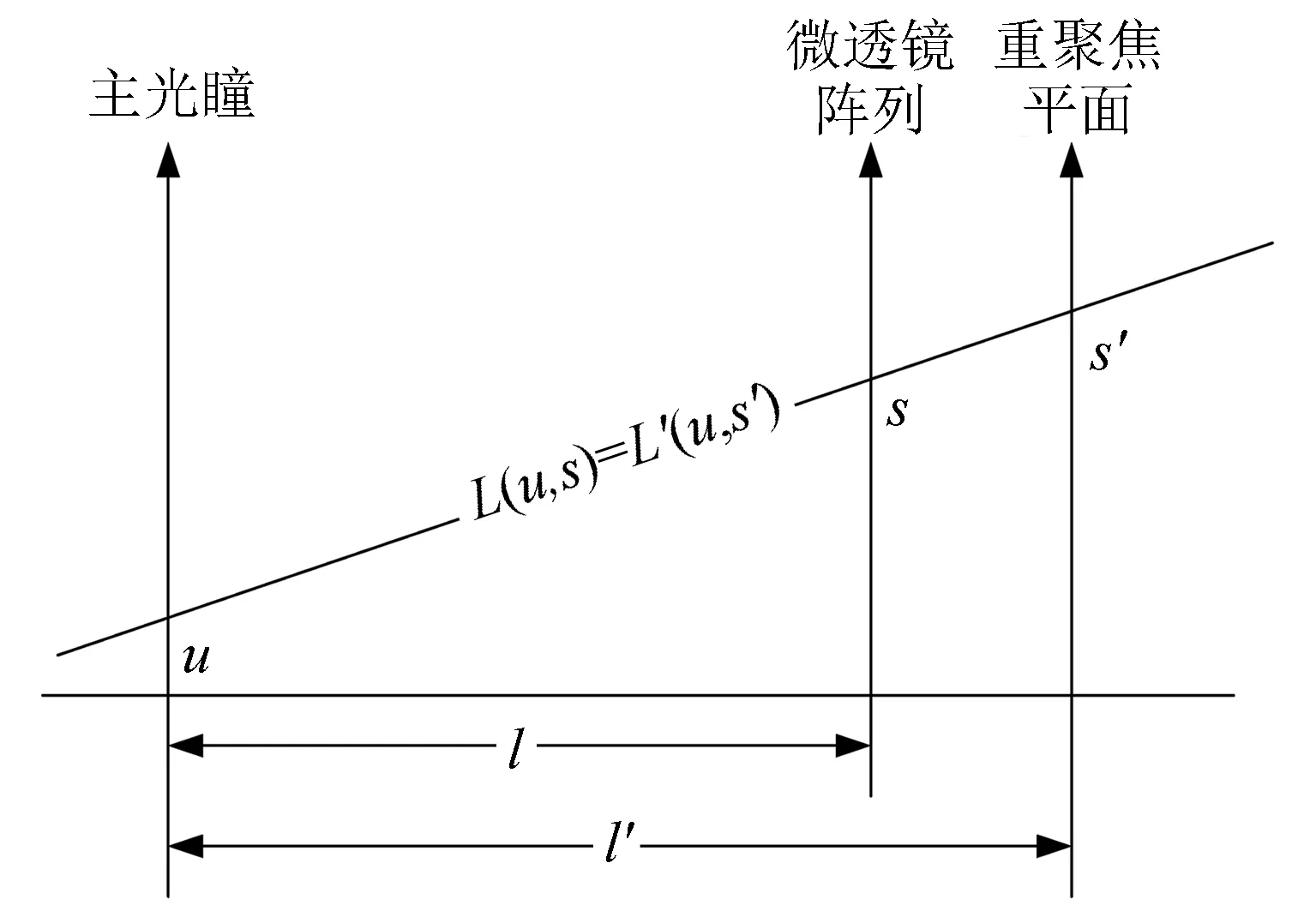
图 3　数字重聚焦Fig.3　Digital refocusing

主透镜与微透镜距离为l， 主透镜与聚焦面距离为l′， 定义两者的关系为

l′=αl.

(1)

重聚焦就是将主透镜与聚焦面间光场的方向进行积分， 如式(2)所示

(2)

(3)

(4)

(5)

将式(4)带入式(5)可得

(6)

式(6)即为对焦至重聚焦面的成像公式.

2　光场成像模型

2.1　物空间模型构建

为了构建出三维成像模型， 实验通过将一幅二维图像以金字塔结构提取图像的有效区域并逐层向后推移， 达到近似构建出三维场景的效果. 以扩展为8个离散面为例， 其物空间模型如图 4 所示.

图 4　物空间模型Fig.4　Object space model

图 5　遮挡模型Fig.5　Occlusion model

这种金字塔模式的物体建立方式可任意调整两个物面之间的间距以及物体的物距， 理论上可以排列出无穷多个物面达到近似建立三维场景的效果.

在对每一物距上的平面进行光场成像时， 由于光线沿直线传播， 前景会对后景有部分遮挡， 因此图像中每一个像素点发出的光在打到主透镜之前要进行遮挡判断， 如图 5 所示.

由于进入不同子孔径的光的方向不同， 遮挡的范围也不同， 所以在成像过程中， 要对每一个子孔径进行遮挡判断. 在图5中， 由于A物面遮挡了部分的B物面， 针对于所选择的子孔径来说，B物面上的阴影区域所发出的光无法进入该子孔径， 故在成像时， 阴影部分的像素点不会进入光场成像系统. 在仿真过程中， 每一个子孔径的光线近似从子孔径的中心进入. 假设B面物点的坐标为(x1,y1,z1)，A面物点的坐标为(x2,y2,z2)子孔径的坐标为(x3,y3,z3)， 则B面物点与子孔径间的直线方程为

(7)

这条光线在经过A物面所在物距z2时， 其空间位置为

(8)

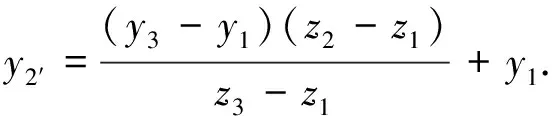
(9)

此时判断(x2′,y2′,z2)是否在A物面上， 若不在A物面上， 则该B面物点可以进入光场成像系统； 若在A物面上， 则该B面物点被遮挡， 无法成像.

2.2　数值孔径匹配

在主透镜成像过程中， 物点与像点遵循高斯成像公式

(10)

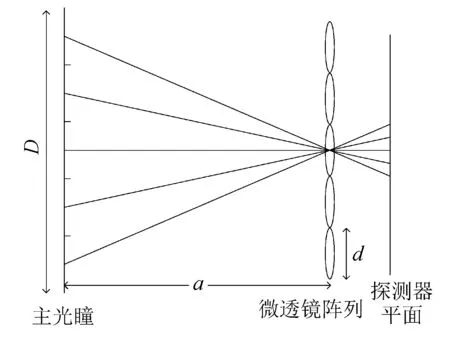
图 6　光场成像模型Fig.6　Light field photography model

式中：u为物距；v为像距；f为主透镜焦距. 微透镜阵列放置于像面处， 探测器位于微透镜阵列后方， 如图 6 所示.

图 6 中为一个主透镜被分为5块子孔径的光场成像模型， 设主透镜孔径大小为D， 像距为a， 微透镜大小为d， 微透镜焦距为f. 由于像距相比于微透镜的大小无穷大， 故来自主透镜的光对于微透镜来说近似于来自无穷远的平行光， 因而探测面应位于微透镜后f处. 为了使每一个微透镜后的宏像素间既不发生重叠， 又要最大程度利用探测器像元数， 每一个宏像素应与相邻宏像素相切， 对应到互相相切的微透镜阵列， 宏像素的大小应为d， 根据相似三角形定理得到

(11)

2.3　离焦物面成像

在实际拍摄物体时， 物面所成像的位置往往不在微透镜阵列所在像面， 根据式(10)， 不同的物距对应有不同的像距. 因此每一物面像素经子孔径打在微透镜阵列处往往是一个光斑， 物面离焦量越大， 在微透镜上所成光斑也越大. 图 7 所示为一个离焦物点经一个子孔径在微透镜上所成的光斑示意图 .

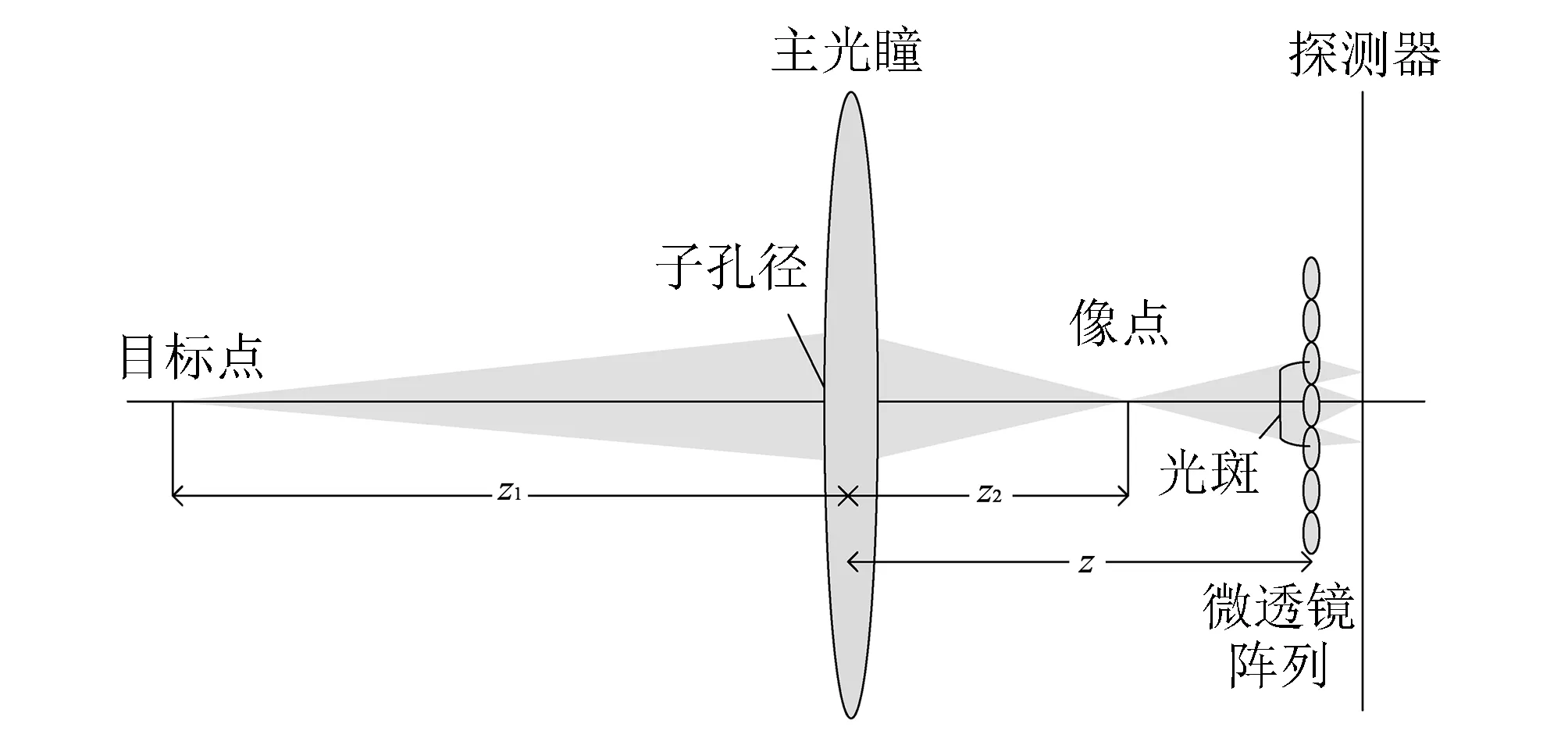
图 7　离焦物点光场成像Fig.7　Optical field imaging of defocused point

图 7 中：z1为物距；z2为像距；z为主透镜及微透镜间的距离， 设子孔径大小为duv， 光斑大小为h， 主透镜焦距为F， 则根据相似三角形定理， 光斑大小的表达式为

(12)

根据式(10)可得

(13)

根据图 7 所示， 光斑打在若干微透镜上， 由于此光斑来自于同一子孔径， 其在探测器上的像元的位置近似为每个微透镜下宏像素的相同位置， 根据光斑在每个微透镜上的权重来分配每个宏像素下对应像元上的能量. 同时， 由于不同物点发出的光可能经过同一子孔径打在同一微透镜上， 因而每一个像元所包含的能量不仅仅来源于一个物点. 所以仿真时针对每一个像元统计打在此像元上的光线条数， 用总能量除以总光线条数即可得到此像元下的灰度值.

3　仿真实验结果与分析

3.1　仿真实验结果

表 1　相机参数

为了验证本文所提出仿真方案的正确性， 以一幅二维图像为例进行仿真. 本实验是在CPU主频为3.4 GHz， 内存为8 G的计算机中matlab2014a仿真环境下进行的. 实验所用图像如图 8 所示， 为256×256， 8bit/pixel.

对图 8 进行本文提出的方式进行光场成像仿真， 将二维图像扩展为40个面， 初始物距为420 mm， 离焦距离为15 mm， 其余面利用金字塔推面模式扩展离散物面有效区域大小并向后挪动物面， 步进为1 mm， 最终得到由40个物面构成的光场图， 如图 9 所示. 根据数值孔径匹配所设置的相机参数如表 1 所示.

图 8　原始图像Fig.8　Original image

图 9　实验所得光场图Fig.9　Light field image in the experiment

根据仿真实验所得到的光场图(图 9)可以看出， 图像中有很多灰度值渐变的小方格组成， 每一个小方格代表一个宏像素， 宏像素下灰度值的不同代表每一子孔径观测到的视角的不同. 图像中间部分离焦距离最小， 在整幅光场图像中最为清晰， 而自图像中心向外扩的部分随着离焦距离的增加， 图像越来越模糊.

为了测试实验模型及光场图像的正确性， 根据式(6)通过调整α值对光场图像进行不同物面的重聚焦处理， 其仿真结果如图 10 所示.

图 10　不同物面的重聚焦结果Fig.10　The results of refocusing on different object plane

3.2　结果分析

本文所建立的三维模型是将二维图像以金字塔模型进行有效面扩展及推面处理， 由图9可以看出， 在距离主透镜最近的部分， 即原始图像的中心部分， 由于较小的离焦量， 在光场图像中能够辨别出图像中的图案. 而图像越靠近四周， 离焦量越大， 在光场图中越模糊. 这是因为离焦量大的物面像素相比于离焦量小的物面像素经子孔径打在微透镜阵列上的数目多， 其所包含的信息分配的宏像素多， 因而呈现出模糊感， 且这种模糊程度随离焦量的变大而加剧.

通过调整α值进行重聚焦处理， 可以得到不同物距的重聚焦结果. 由式(1)可知， 随着α值的减小， 重聚焦平面对应的像距也随之减小. 根据式(10)可知， 当重聚焦平面对应的像距减小时， 其对应的物距逐渐增大， 在图10中表现为清晰部分随着α值的减小逐渐向图像四周扩展， 而中心部分相对四周部分物距小， 逐渐变得模糊. 这种现象与所建立的三维场景相符.

4　结　论

提出一种有效获得三维场景光场数据的仿真方法， 利用金字塔模式对二维图像进行有效面扩展及物面推移处理. 在光场成像过程中判断前景对后景的遮挡以及离焦图像在成像过程中的近似处理得到三维光场图像. 为了验证本文所提出的三维场景建立方法以及所得到的光场图像的正确性， 通过调整α值对图像进行不同物距上的重聚焦处理. 仿真结果表明了本文所提出的三维场景模型的正确性， 对于以后在三维场景下进行光谱成像实验、 深度估计及其他光场成像实验的数据获取有一定的参考价值.

参考文献：

[1]Gershun A. The Light Field[J]. Studies in Applied Mathematics, 1936, 18(1-4)： 51-151.

[2]Levoy M, Hanrahan P. Light field rendering[C]. Conference on Computer Graphics and Interactive Techniques. ACM, 1996： 31-42.

[3]Zhang C, Hou G, Sun Z, et al. Efficient auto-refocusing of iris images for light-field cameras[C]. IEEE International Joint Conference on Biometrics. IEEE, 2014： 1-7.

[4]Ikeoka H, Murata T, Okuwaki M, et al. Depth estimation for automotive with tilted optics imaging[C]. IEEE International Conference on Image Processing. IEEE, 2015： 3852-3856.

[5]Garbe C, Baker H, Jähne B. Light-field camera design for high-accuracy depth estimation[C]. SPIE Optical Metrology. 2015： 952803.

[6]Zhou Z, Xiangli B. Snapshot Multispectral Imaging Using a Plenoptic Camera with an Axial Dispersion Lens[M]. 2014.

[7]Raghavendra R, Busch C. Presentation attack detection on visible spectrum iris recognition by exploring inherent characteristics of Light Field Camera[C]. IEEE International Joint Conference on Biometrics. IEEE, 2014： 1-8.

[8]Ng R, Levoy M, Brédif M, et al. Light field photography with a hand-held plenoptic camera[J]. Computer Science Technical Report CSTR, 2005, 2(11)： 1-11.

[9]Favaro P. A split-sensor light field camera for extended depth of field and superresolution[C]. SPIE Photonics Europe. International Society for Optics and Photonics, 2012： 843602-843609.

[10]Park H, Park M K, Kim M, et al. Light-field camera using fast switchable micro-lens array for simultaneous 2D/3D image acquisition[C]. Lasers and Electro-Optics Pacific Rim. IEEE, 2015： 1-2.

[11]Bae S J, Kim J W, Park S, et al. Camera array type plenoptic moving picture acquisition system[C]. The Workshop on Information Optics. 2016： 1-3.

[12]Ghasemi A, Scholefield A, Vetterli M. On the accuracy of point localisation in a circular camera-array[C]. Image Processing (ICIP), 2015 IEEE International Conference on. IEEE, 2015： 981-985.

[13]Ciurea F, Lelescu D, Chatterjee P, et al. Adaptive Geometric Calibration Correction for Camera Array[C]. Is&t International Symposium on Electronic Imaging, 2016.

[14]Birklbauer C, Bimber O. Panorama light-field imaging[J]. Computer Graphics Forum. 2014, 33(2)： 43-52.

[15]Park B, Kirmani G A, Raskar R, et al. Apparatus and method for processing light field data using a mask with an attenuation pattern： U.S. Patent 9,143,678[P]. 2015-9-22.

[16]Georgiev T, Yu Z, Goma S. Lytro camera technology： theory, algorithms, performance analysis[J]. Proceedings of SPIE - The International Society for Optical Engineering, 2013, 8667(15)： 86671-86681.