基于MILP模型和QPSO算法的绿色物流调度方法*

刘　岚，　兰小毅

(西安工业大学 经管学院，陕西 西安 710021)

为了应对竞争激烈的全球市场，厂家选择一个有效的供应链网络(supply chain network，SCN)来降低库存成本变得尤为重要.供应链是规划、实施和控制货物或服务的流程[1].准时制(just-in-time，JIT)是其中一种供应链策略，它通过频繁的生产，大大减少了工作流程中的库存，从而提高了企业的生产效率[2].然而，频繁进行小规模生产，对运输需求的响应能力要求更高，会导致环境污染和运输成本上升等问题.在准时制的基础上，[3]提出了一种多准则决策模型，实现产品的生产、质量、价格、成本、设备、技术和交货都能满足客户需求和出口质量标准.[4]提出了一种新的准时制决策，研究结果表明准时制对丰田工厂的销售、设计、改进和生产产生了积极的影响.[5]在双层非线性优化模型的基础上提出了决策支持系统.为解决准时配送问题，[6]在三级分销网络的基础上开发了多目标数学模型.此前传统的数学建模并未涉及对环境的影响.考虑到供应链管理相关过程对环境的影响，在传统的供应链管理中加入“绿色”概念.物流作为与SCM相关的主要组成部分，直接影响环境污染源——温室气体排放.尽管对绿色物流的研究在过去有所增加，但目前实际物流中很少遵守环境约束.从绿色的视角来看，模糊的多目标化技术是解决绿色供应链网络的主要方法.通常，所提出的数学模型目的是在两个相互冲突的目标之间进行权衡，即将二氧化碳当量作为一个指标来量化物流活动对环境的影响，以总成本最小化和环境影响最小化为目标，实现一个优化的整合前向和反向闭环的供应链网络[7].经典的生产和分配模型关注的是成本最小化，这取决于生产的约束.考虑到绿色物流的目标和约束，将产生新的组合优化模型.为此，本文开发了一个多目标的混合整数线性规划模型(mixed integer linear programming, MILP)来构建物流调度网络模型，包含了多个制造工厂、配送中心、零售商和产品属性.该模型的目标是尽量减少在配送中心和经销商处的交货时间，以及最小化碳排放.为了求解该MILP模型，本文采用了一种量子粒子群优化(quantum particle swarm optimization,QPSO)算法，以此快速地获得最优调度方案.

1　构建物流调度的MILP模型

1.1　物流网络模型

物流网络模型分为3个级：第1级为制造商，第2级为分销商，第3级为经销商[8].在开发物流调度模型时，建立了以下假设：(1) 模型是专为多个制造商、分销商、经销商、产品进行规划调整的；(2) 需求量与初期的需求有关；(3) 货物、分销商、经销商和供应商的位置是固定的；(4) 制造商、分销商和经销商的生产销售能力是已知的；(5) 各期的持续时间等于生产时间的总和；(6) 在配送的开始或结束，经销商没有库存；(7) 在交付给分销商之前，产品暂时存放于经销商；(8) 运输方式与各类型固定容量的卡车相关；(9) 假设所有产品品质完全合格，也就是说在系统里没有报废、返工或退回.另外，模型中的一些限制约束：(1) 在执行期间所有的需求必须被满足；(2) 生产时间被限制；(3) 每个合格产品的库存能力有限；(4) 制造商、经销商和分销商的能力有限.模型的参数和决策变量如表1所示.

表1　模型中的参数及含义

1.2　构建MILP模型

物流调度的MILP模型包含目标函数和约束条件，分别表述如下.

第一个目标函数，即在配送中心和经销商之间，最小化产品交付时间的表达式为：

第二目标函数，即在整个物流网络中，总碳排放量最小化的表达式为：

这里设定了2个目标函数，其中总碳排放量最小化将导致交货期增加，而交付时间最小化会增加运输次数，从而对环境造成不利影响.用户可根据具体需求设定两个目标函数的权重构成最终目标函数，此时需要对minZ1和minZ2进行归一化，总目标函数表示如下：

O=k·Norm(minZ1)+(1-k)·Norm(minZ2),

式中Norm(minZ1)表示minZ1的归一化，即实际交付时间与允许最大交付时间的比值.同样，Norm(minZ2)为实际碳排放量与最大排放量的比值.

碳排放量的计算采用广泛认可的温室气体协议方法.每个产品的等效碳排放量可以作为一个线性函数来计算，它取决于运载车辆行驶距离(公里)和碳排放(每公里二氧化碳排放量).我们将这个碳排放模型应用于给定的供应模式，而碳排放与运输产品的数量成比例.

在分销商处的库存表示为(注意在每个分销商的计划开始和结束时没有库存)：

在规划期间内，向分销商运输货物的总输入和输出之间的平衡关系为：

在t时间段内，总运输量没有超过产品生产能力的关系表示为：αijpt+βjkpt≤χipt.

确保交付给配送商和经销商的价值为非负数表示为：αijpt,βjkpt,χipt≥0.

2　基于QPSO算法求解MILP模型

对于MILP模型的求解，通常采用数学规划软件GAMS中的CPLEX模块[9].由于目前各种智能优化算法的发展，出现了一些快速且高精度的优化算法，为此本文采用了一种QPSO算法来求解物流调度的MILP模型.近些年，产生了一种新的进化算法，称为量子进化算法(QEA)，在寻优方面优于遗传算法.由于传统QEA中通过量子旋转门来更新量子角增量，操作复杂且更新角度固定，使其容易陷入局部最优.为此，学者引入了PSO算法中的位置更新公式替代QEA中的量子旋转门来更新角增量，形成量子粒子群优化(Quantum-PSO，QPSO)算法[10].

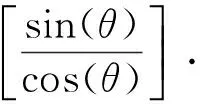
QPSO使用PSO的群智能概念，将群体中的所有多量子比特视为智能种群，称为量子群.首先，QPSO找到局部最佳量子角，并从局部最佳量子角中找到全局最佳量子角.然后根据这些值，用量子角更新公式更新量子角.基于QEA的QPSO步骤如下：

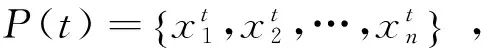
(3) 计算P(t)的适应度，其通过适应度函数F，对每个二进制解P(t)进行评估，确定本次迭代中的个体最佳和全局最佳.

(4) 使用以下PSO位置更新公式替换传统“量子门更新Q(t)”步骤，量子角度更新公式为：

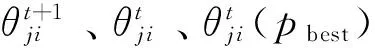
3　实验及分析

3.1　实验设置

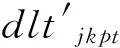
3.2　性能分析

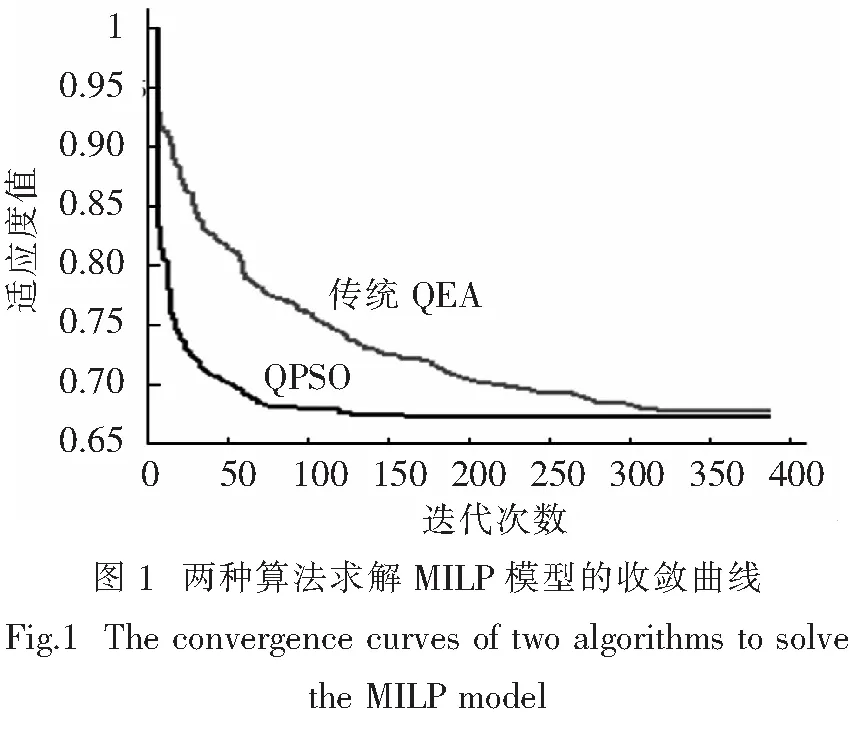
将传统QEA与本文应用的QPSO对求解物流调度MILP模型的能力进行比较.设定一个物流调度方案的总目标函数O，其中对交付时间和碳排放量这两个目标赋予相同的权重，即系数k设置为0.5.在不同迭代次数下的收敛结果如图1所示.QPSO的收敛速度较快，在200次迭代之后基本收敛到最优解，而传统QEA则需要大约320次才能收敛，且最终解的质量略微低于QPSO.这是因为QPSO采用了PSO位置更新方程和动态惯性权重，有效提高了收敛速度和收敛精度.

将本文方法与[6]提出的物流调度优化方法进行比较.[6]方法中的物流模型与本文方法一样，都采用三级结构，但该方法只考虑一个目标.为了公平比较，本文设定的目标函数也作为文献[6]方法的目标.

实验中设定权重系数k为[0.4，0.6]之间不同的值，以此构建不同的总目标函数O.统计各种方法获得的最终调度方案的目标函数值、归一化交付时间Norm(minZ1)和归一化碳排放量Norm(minZ2)，结果如表2所示.随着k值的增加，Norm(minZ1)值随之减低，而Norm(minZ2)值随之增加.这是因为k值增加，总目标函数中对Norm(minZ2)的考虑比重降低，而更看重Norm(minZ1)值，所以优化模型优先考虑降低Norm(minZ1)值.从对比结果来看，在不同的k值下，本文方法获得的结果都优于[6]方法.这是因为本文将物流调度问题科学建模为一个MILP模型，并通过智能算法进行求解，获得了最优的调度方案.

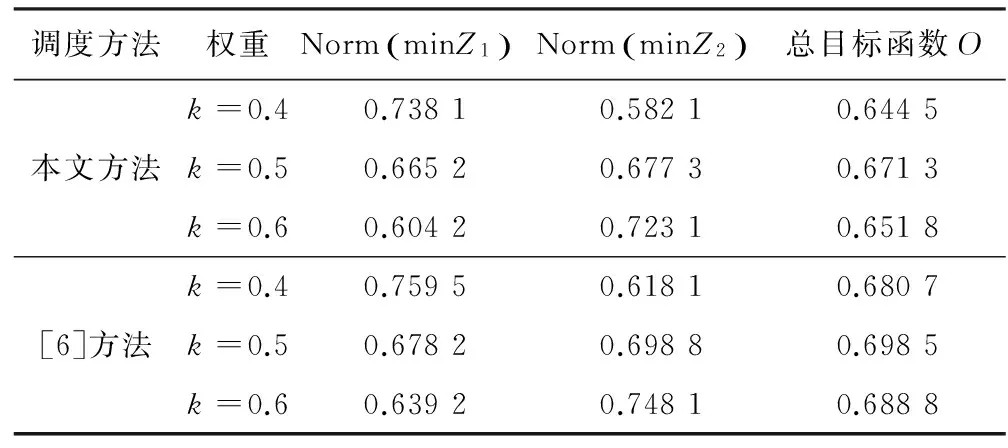
表2　物流调度方案的性能结果

4　结　论

基于MILP模型和QPSO算法提出一种求解物流网络中物流调度方案的方法，以优化供应链时效性和降低对环境的影响.具体目标是优化从制造商到配送中心、从配送中心到经销商的交货期，并尽量减少整个物流系统中的碳排放量.为了获得有效调度方案，将调度问题构建为一个MILP模型，并利用一种快速智能优化算法QPSO来求解该模型.在一个汽车销售物流网络上的实验取得了较好的结果.

[1]尹小悦, 王娟, 陈昭玖. 基于模糊评价的绿色供应链管理可行性评估方案[J]. 湘潭大学自然科学学报, 2016, 38(4):116-120.

[2]张鑫磊. 准时制生产方式视角下的物流管理研究[J]. 物流工程与管理, 2016, 38(10):47-48.

[3]WU K J, TSENG M L, CHIU A S F, et al. Achieving competitive advantage through supply chain agility under uncertainty: A novel multi-criteria decision-making structure[J]. International Journal of Production Economics, 2016, 19(4):132-137.

[4]覃爱民, 夏松. 基于JIT的装配式建筑FDC阶段供应链集成管理研究[J]. 信阳师范学院学报:自然科学版, 2017, 30(3):489-493.

[5]MEMARI A, RAHIM A R B A, AHMAD R B. Production planning and inventory control in automotive supply chain networks[C]// International Conference on Industrial, Engineering and Other Applications of Applied Intelligent Systems. Springer International Publishing, 2014:430-439.

[6]EREN Özceylan, TURAN Paksoy. Fuzzy multi-objective linear programming approach for optimising a closed-loop supply chain network[J]. International Journal of Production Research, 2013, 51(8):2443-2461.

[7]RYU J H, HAN J H, LEE I B. Development an optimization model for green supply chains: integration of CO2disposal and renewable energy supply[J]. Computer Aided Chemical Engineering, 2012, 30(3):317-321.

[8]秦小辉. 基于碳交易的已存供应链物流网络优化研究[J]. 计算机应用研究, 2017, 34(5):1374-1378.

[9]依俊楠, 刘攀, 徐小伟,等. 基于混合整数线性规划模型的水电站日优化调度研究[J]. 水电能源科学, 2011, 29(7):33-35.

[10]XIN J, XIAO F H. A quantum-PSO-based SVM algorithm for fund price prediction[J]. Journal of Convergence Information Technology, 2012, 7(3):267-273.