体育联赛中基于GSO算法的赛程优化方法*

曾芳桂，　赵　曼

(1.武汉大学 体育部，湖北 武汉 430070；2.中国地质大学(武汉) 计算机学院，湖北 武汉 430074)

目前有多种类型的图形化体育联赛赛程机制，如单轮巡回赛、双轮巡回赛等[1].这些比赛的不同之处是赛程、比赛数量和比赛形式.例如，世界杯决赛有两个阶段:小组赛阶段和淘汰赛阶段.在小组赛阶段，有8个小组，每个小组有4个队.每个队都有一场循环赛，即每个队都要和小组内的其他队进行一场比赛.然后，每组中只有前2支球队会进入淘汰赛阶段.淘汰赛是一场单淘汰赛，各队进行一场一次性比赛.在足球、篮球、棒球等联赛中，每个队在两场比赛中互相对抗，一场是主场，另一场是客场[2].对于主客场赛制的联赛，赛程的安排直接影响各队的行程安排.因此，如果赛事组织者能够在日程安排上帮助减少一些交通等费用，这将是有益的[3].在体育联赛中，有很多变量影响各个队伍的成本，比如转场方式、转场距离、转场次数、转场顺序等.因此，影响转场成本的比赛调度问题已经成为多年来重要的优化问题.目前，一些学者提出了一些赛程调度方案.例如，[4]以最小化所有队伍的行程距离为目标，提出了一种基于蒙特卡洛的赛程优化方法.[5]提出一种基于集成约束规划的赛程优化方法，用来最小化每个队伍的转场次数.

本文以最小化所有队伍的总转场次数为目标，提出一种基于群搜索优化(group search optimization, GSO)算法的赛程优化方案.将赛程安排通过由转场序列矩阵构建的赛程序列矩阵来表示，然后通过GSO算法获得最优的转场矩阵，最终形成最优赛程调度方案.在不同队伍规模的比赛场景中进行实验，结果表明本文方案能够有效降低转场次数，具有可行性.

1　联赛赛程描述

1.1　赛程约束与优化目标

每支队伍的转场次数为从其主场出发到比赛结束返回时的转移城市总次数.在主场的比赛叫做主场比赛，在对手城市的比赛叫客场比赛.优化目标是最小化所有队伍的总转场次数，并满足以下限制:(1) 这里的比赛日程是一个旅行锦标赛问题(TTP)[6];(2) 每个队在一周内最多只能打一场比赛，而且每周都必须有同样数量的主场比赛和客场比赛;(3) 如果在一周后没有主场比赛，球队不会回到主场;(4) 每队的比赛顺序中最多允许连续三场主场比赛或连续三场客场比赛.

1.2　赛程调度表示

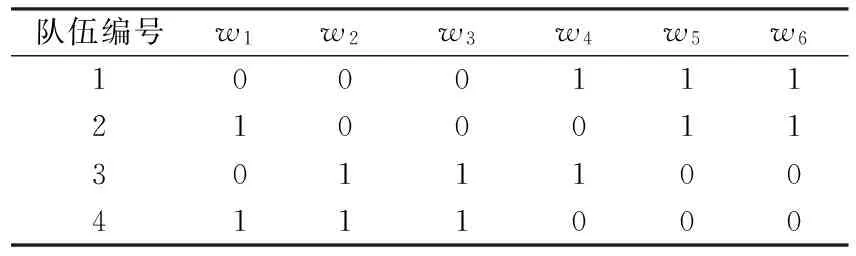
在这项工作中，赛程安排问题分为两部分:队伍转场和队伍赛程.n队比赛的队伍转场和赛程分别由矩阵A和B表示，其中n是偶数.队伍转场A由n个队伍的n个转场序列组成，其中转场序列由0和1组成，0代表主场，1代表客场.A(i,j)中的元素代表了队伍i在wj周上的比赛类型.例如，一个可能的转场序列如表1所示.从问题描述来看，每一个转场序列最多可以有3个连续的0或3个连续的1.在获得所有的转场序列后，可以形成队伍转场矩阵.表2显示了4个队伍比赛中的一个转场矩阵例子.很明显，任何队伍都有不同的转场序列.接下来，队伍赛程矩阵也由n个赛程序列组成.队伍i的赛程序列是一个从1到n的序列，除了编号i.B(i,j)表示在wj周对阵队伍i的队伍编号.例如，表3所示为4个队伍比赛的一个可能的赛程序列.在获得所有赛程序列后，可以生成队伍赛程矩阵.表4显示了一个4个队伍比赛的队伍赛程矩阵例子.表4中每个赛程矩阵的元素B(i,j)依赖于表2中的队伍转场矩阵.例如，B(1,3)可以等于4，因为A(1,3)不等于A(4,3).一般来说，B(i,j)可以等于k，当且仅当A(i,j)不等于A(k,j)时.因为在每一场比赛中,一个队伍为主场比赛，而另一个队伍则为客场比赛.

表1　队伍1可能的转场序列

表2一个4队参加比赛的队伍转场矩阵A例子

Tab.2TransitionmatrixAofamatchwithfourteamsparticipating

队伍编号w1w2w3w4w5w61000111210001130111004111000

表3队伍1可能的赛程序列

Tab.3Schedulesequenceofteam1

队伍编号w1w2w3w4w5w61234234

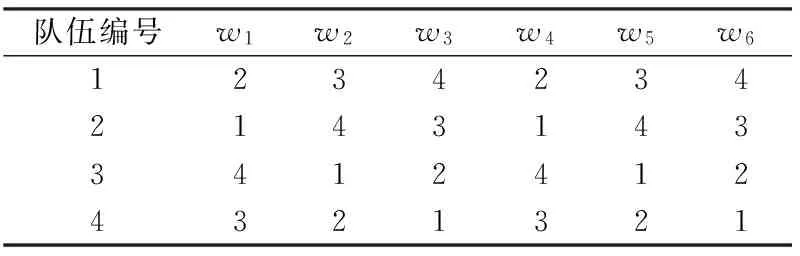
表4　 一个4队参加比赛的队伍赛程矩阵B例子

2　基于GSO生成最优调度方案

2.1　个体编码

利用GSO算法和序列交换方法解决体育转场联赛赛程调度问题.在初始化GSO算法中的个体时，首先随机生成前n/2行序列，然后用序列交换方法生成其他n/2行序列，以此构建一个GSO个体的方案编码.序列交换用于生成另一半的转场序列，即将所有队伍的主/客场进行互换.如表5所示，显示了一次交换之前和之后的转场序列.

表5　一次交换之前和之后的转场序列

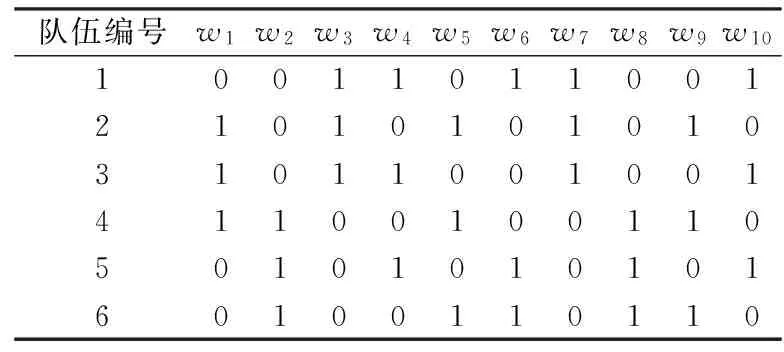
表6　在6个队伍比赛中随机生成的转场序列

例如，在6个队伍比赛案例中，生成一个初始个体的例子如下所示.首先，在赛制约束下通过随机选择生成前3个转场序列，如表6中上3行所示.在此之后，分别用1、2、3组的转场序列，通过交换方法生成剩余队伍4、5、6的转场序列，如表6中下3行所示.

2.2　GSO算法

对于求解NP困难问题，启发式智能算法最为有效[7].其中，GSO算法包含3个操作，即发现者操作、搜索者操作和游荡者操作[8].在迭代过程中，将具有最佳适应度值的成员选为发现者.将适应度值高于阈值的多个成员选为搜索者.将适应度值低于阈值的多个成员选为游荡者.

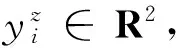
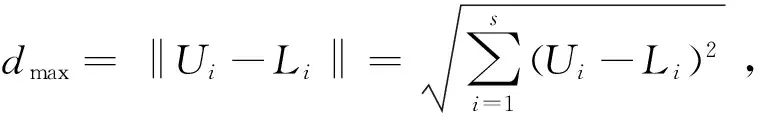
式中，yzero表示零度扫描，yright表示右边扫描，yleft表示左边扫描，r1∈R1为均值为0、方差为1的正态分布随机数，r2∈Rs-1为(0,1)内的一个随机序列.然后，计算发现者搜索到的3个新位置的适应度，并移动到具有最优适应度的位置.如果新位置都不如当前位置，则将其头转向一个新角度λz+1=λz+r2γmax，其中γmax表示最大转向角.如果在ɑ次迭代结束后，发现者没有找到一个更好的位置，则停止搜索过程且保持不动，即λz+ɑ=λz.

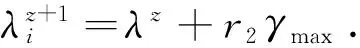
2.3　优化转场序列及生成调度方案

在利用GSO算法优化转场序列时，对传统GSO进行改进，即通过一个变异操作对发现者进行变异来生成游荡者，而不是通过适应度阈值判断来生成，这样有利于跳出局部最优解，提高算法的全局搜索能力[10].

变异过程通过改变转场矩阵A中某一行和列的元素来实现.首先，通过GSO算法获得当前发现者，即以n×(2n-1)形式的转场序列矩阵来表示；然后，随机选择矩阵中wj列(周)和n行(队伍)对应的元素，将其从1变到0或从0变到1.之后，根据比赛属性的映射关系，将相关的wj和n以同样的条件改变.

在通过改进GSO得到最优的转场序列矩阵后，根据转场序列，通过一个赛程方案生成算法来构建所有队伍的赛程时间表.算法1给出了赛程方案生成算法的伪代码.

算法1:赛程方案生成算法输入:所有队伍的转场序列(A[1:n,1:n-1])输出:赛程矩阵1 for(i=1:n)2 if(i>1) then添加队伍i之前的队伍的赛程;3 endif;4 for(m=1:n-1)5 if(B[i,m]满足约束条件) then添加赛程序列B[i,m];6 endif;7 whilemin(B[i,:]=0)8 nteam←missingteanm(B[i,m]);9 if(nteam==i+1) then构建队伍i-1的赛程序列;10 else构建队伍i的赛程序列;11 endif;12 endwhile;13 endfor;14endfor;15输出赛程矩阵B[1:n,n:2n-2]←B[1:n,1:n-1];

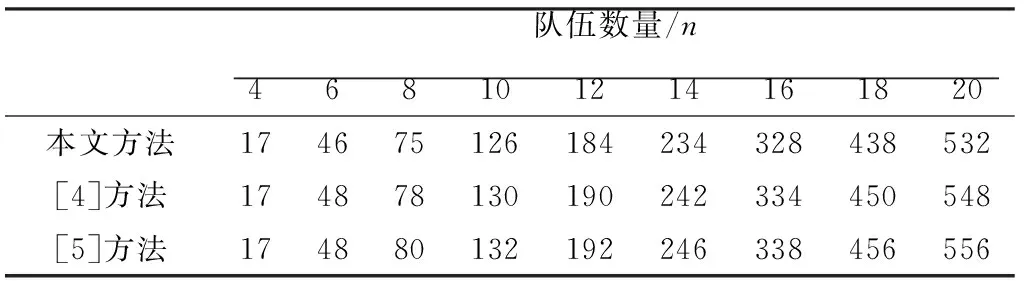
表7　不同队伍数量下赛程方案的总转场次数

3　实验及分析

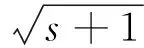
将本文方法与[4]提出的蒙特卡洛赛程安排方法和[5]提出的集成约束规划方法进行比较.实验中，设置队伍数量n从4到20不等，执行各种方法获得最优的赛程方案，并计算各种方案中所有队伍的总转场次数.比较结果如表7所示.

从表7可以看出，本文方法获得的赛程方案中总转场次数最小，且随着比赛队伍数量的增加，其优势更加明显，这证明了本文方法的有效性.这是因为本文采用了GSO算法来进行寻优，并通过变异机制来获得游荡者，增强了寻优能力.此外，本文中的交换过程可以减少运行时间，算法只需要随机选择个体的前n/2行转场序列，然后使用交换过程生成剩余序列，得到的整体转场序列也满足比赛约束条件.如果没有交换过程，算法必须随机选择所有转场序列，得到的解可能不能满足约束条件，影响后续的寻优过程.

4　结　论

为了提高各种体育联赛的赛程经济性，将赛程安排方案编码为一个赛程矩阵.在满足赛制约束条件下，通过结合序列交换和GSO算法来生成联赛赛程安排方案，最小化了所有参赛队的转场次数，以此来降低比赛成本.在与其他现有方法的比较中，本文方法表现出了优越的性能.在今后的研究中，将考虑转场距离等因素，使其更加贴合实际情况.

[1]周轶枫, 杨滨峰. 利用卷积神经网络的体育视频运动员检测[J]. 湘潭大学自然科学学报, 2017, 39(1): 95-98.

[2]张玉国, 姜立嘉. 我国高校竞技体育赛事资源优化配置研究——以高校篮球联赛为例[J]. 北京体育大学学报, 2013, 36(11): 102-107.

[3]HUNG J C, YEN N Y, JEONG H Y, et al. Adaptive mechanism for schedule arrangement and optimization in socially-empowered professional sports games[J]. Multimedia Tools & Applications, 2015, 74(14):5085-5108.

[4]都扬扬, 木仁. 具有主客场赛制的各大联赛赛程优化安排与设计[J]. 中国管理科学, 2015，23(1):171-175.

[5]LARSON J, JOHANSSON M, CARLSSON M. An integrated constraint programming approach to scheduling sports leagues with divisional and round-robin tournaments[C]// International Conference on AI and OR Techniques in Constriant Programming for Combinatorial Optimization Problems. Springer International Publishing, 2014:144-158.

[6]韦炜, 藤村茂, 席裕庚. 求解旅行锦标赛问题的改进混合局部搜索算法[J]. 计算机仿真, 2012, 29(10):252-255.

[7]何常胜, 赵小河, 陈安. 基于遗传算法和后代校正的WSN覆盖和连通性优化方案[J]. 湘潭大学自然科学学报, 2016, 38(2): 89-93.

[8]熊聪聪, 郝璐萌, 王丹,等. 一种基于差分策略的群搜索优化算法[J]. 计算机科学, 2017, 44(2):250-256.

[9]AKHAND M A H, JUNAED A B M, HOSSAIN M F, et al. Group search optimization to solve traveling salesman problem[C]// International Conference on Computer and Information Technology. IEEE, 2013:72-77.

[10]CHEN D, WANG J, ZOU F, et al. An improved group search optimizer with operation of quantum-behaved swarm and its application [J]. Applied Soft Computing Journal, 2012, 12(2): 712-725.