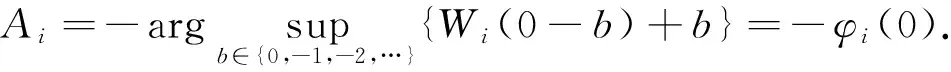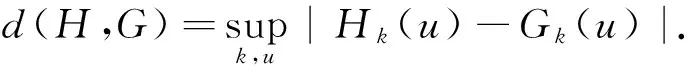离散更新风险模型中的红利与注资的最优控制*

陈　格，　陈源坪，　王一婧

(1.湘潭大学 数学与计算科学学院, 湖南 湘潭 411105;2.中国银行 广州花都分行，广东 广州 510800 )

自1957年De Finetti[1]提出最优红利问题以来, 众多学者对该问题作了大量研究.为了降低公司的风险, 有学者认为最优的红利策略应该结合考虑赤字惩罚和注资. 关于考虑注资及罚金的红利优化问题, 参考文献[2]～[4].

本文基于更新风险模型引入红利支付、注资和发生赤字时的惩罚，研究分红和注资的最优控制策略. 当公司出现负盈余时, 股东可以选择破产, 也可以选择注资. 因此最优控制策略涉及最优停时, 即宣布破产的最优时刻. 我们使用压缩映射原理得到最优值函数是离散HJB 方程组的唯一解. 此外, 我们得到了最优控制策略的一些性质和破产的最优条件, 并提供一个高效的算法来获得最优策略和最优值函数，其方法可参看文献[5]. 关于更新风险模型的讨论可见文献[6].

在离散更新风险模型中, 盈余过程 {U(t),t∈N}定义为:

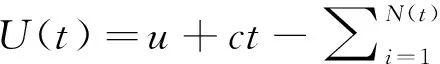
(1)

式中：初始盈余u是一个非负整数；正整数c表示每个时间段所收的保费；随机变量Xi表示第i次索赔额. 它们是独立同分布的, 其共同的概率分布为f(k)=Pr(Xi=k)(k∈N+). 计数过程 {N(t);t∈N}表示到时间t为止的索赔次数N(t)=max{n:T1+T2+…+Tn≤t}, 其中索赔时间间隔Ti是独立同分布的, 且为正整数值, 其共同概率分布为p(k)=Pr{Ti=k}(k∈N+). 因此,N={N(t)} 是一个一般的更新过程. 进一步假设 {Ti;i∈N+} 和 {Xi;i∈N+}是独立的.

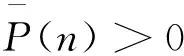
本文基于模型(1)以及相应的延迟更新模型考虑分红和注资问题.定义μt(t∈N) 为t时刻的分红,νt(t∈N)为t时刻的注资. 假设 {μt} 和{νt} 是非负整数序列. 控制策略 {(μt,νt),t∈N}是可容许的, 如果它满足： (i) 对于任意时刻t的分红不会导致负盈余 ; (ii) 分红和注资不能同时进行(如果νt>0 那么μt=0; 如果μt>0 那么νt=0); (iii) 任意时刻t的分红或注资为Ft可料的, 这里Ft是一个σ-代数, 且它包含了时刻t及以前所有的信息量.

假设 {(μt,νt),t∈N}是可容许的控制策略, 令σt=μt-νt. 那么, 当σt>0时,σt表示为分红; 当σt<0时, -σt表示为注资; 当σt=0时, 意味着在t时刻既没分红又没注资. 因此,可容许策略表示为Φ={σt,t∈N}, 则受控制盈余过程(T1的概率分布为gi(k) (i∈N}))定义为:

(2)

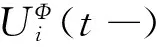
假定Φ*={σ0,σ1,…} 是盈余过程 (2)中的最优控制策略. 显然，σt会受到距离s(t)和t时刻前一瞬间的盈余的影响, 即最优策略是关于这两个变量的函数. 我们用φs(u)来表示这个函数, 其中u表示t时刻前一瞬间的盈余, 即σt=φs(u)，所以我们也可以表示最优控制策略为：

Φ*={φs(u),s∈N,u∈Z}.

(3)

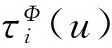
当索赔导致负盈余时, 股东要么宣布破产要么注资. 我们将给出最优破产条件. 因为在初始时刻可以注资, 所以允许负的初始盈余.

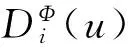
本文还考虑任意注资前发生赤字时有一个常数罚金(用Λ表示). 因此, 值函数定义为:

式中I(A) 为事件A的示性函数,i∈N,u∈Z.

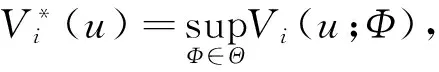
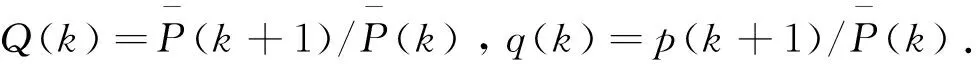
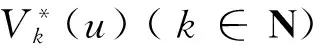
(4)

其中k∈N,u∈Z,Su={u,u-1,…}∪{0}.

证明假设Φ={φi(u)}∈Θ*是最优的.应用全概率公式， 对所有的n=0,1,2,…, 有

(5)

根据(5)可得(4)成立. 另外, 由于Φ的最优性, 当u≥0时,φi(u)∈{u,u-1,…}; 当u<0 时,φi(u)∈{0,u,u-1,u-2,…}.

对于任意的策略Φ={φi(u)}∈Θ*, 我们对值函数Vi(u) 进行变换，其像函数定义为

(6)

那么, 对于任意i∈N和u∈Z, 由(5)可得到

Vi(u)=Wi(u-φi(u))+φi(u).

(7)

根据(6)和(7), 像函数Wi(u)满足下列方程组:

Wi(u)=Q(i)r[Wi+1(u+c-φi+1(u+c))+φi+1(u+c)]+

(8)

对于任意i∈N和u∈Z, 在与Θ*中的策略对应的所有像函数中， 最大者称为最优像函数.

定理2假设Φ={φi(u)}∈Θ*,Vi(u) 是其值函数, 且Wi(u) 是相应的像函数. 那么,Wi(u) 是最优的, 当且仅当Φ是最优的控制策略.

证明首先, 假定Wi(u) 最优. 由(6)和(7)知当u<0 时Wi(u)=0；当u∈N有

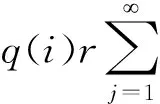
不难发现上式等价于

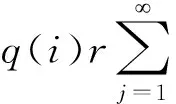
(9)

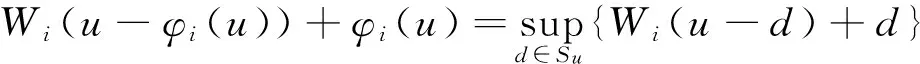
(10)

由(10)和(7)知Vi(u) 是最优值函数. 因此, 策略Φ最优.

相反地, 如果Vi(u) 是最优的, 那么(6)中的Wi(u) 显然是最优的像函数.

定理3Θ*中的最优策略满足

(11)

其中,R表示不小于R的最小整数 , 且

(12)

证明当u≥0时, 由(10) 可得

(13)

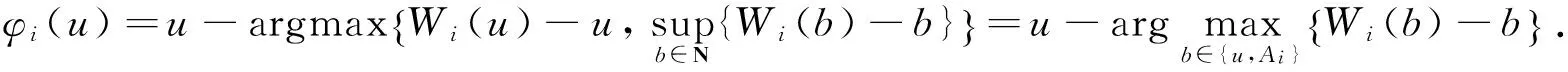
上式等价于

(14)

由于Wi(u)=0, 所以(11)可由(13)和(14)得出.

当盈余处于两边界之间时, 注入资金Ai-u使盈余达到Ai. 当盈余 处在Ai上时, 分红u-Ai给股东.

定理4假设 0

[1]De FINETTI B. Su un’impostazione alternativa della teoria collettiva del rischio[C]. Transactions of the XVth international congress of Actuaries, 1957, 2(1): 433-443.

[2]LOEFFEN R L, RENAUD J F. De Finetti’s optimal dividends problem with an affine penalty function at ruin[J].Insurance: Mathematics and Economics,2010, 46(1): 98-108.

[3]LIANG Z, YOUNG V R. Dividends and Reinsurance under a penalty for Ruin[J].Insurance: Mathematics and Economics,2012, 50: 437-445.

[4]ZHOU M, YUEN K C. Optimal reinsurance and dividend for a diffusion model with capital injection: Variance premium principle[J].Economics Modelling, 2012, 29: 198-207.

[5]TAN J, YUAN P, CHENG Y,et al. An optimal dividend strategy in discrete Sparre Andersen model with bounded dividend rates[J].Journal of computational and Applied Mathematics, 2014, 258: 1-16.

[6]谭激扬,邓丽,杨向群. Sparre Andersen风险模型中的重置保证再保险(英文)[J]. 湘潭大学自然科学学报, 2013, 35(2):1-9.