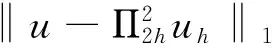定常非线性薛定谔方程的有限元方法超收敛估计*

王建云,　田智鲲

(1.湖南工业大学 理学院, 湖南 株洲 412007; 2.湖南工程学院 理学院, 湖南 湘潭 411104)

超收敛分析是提高有限元方法数值精度和效率的一种强有力的工具, 国内外许多学者做了大量的研究[1-4]. 薛定谔(Schrödinger) 方程是量子力学最基本的方程, 在原子、分子、非线性光学、等离子物理、电磁波理论、核物理等领域中被广泛应用. 关于其数值求解方法有许多的研究[5-9], 而在其超收敛方面的研究不是很多[10-12]. 在本文中, 考虑如下二维定常非线性薛定谔方程：

(1)

式中Ω⊂R2为矩形区域, 未知函数u(x) 和右端项函数f(x) 都为复数值, 势能函数V(x)∈L(Ω) 为实数值且非负, 即存在某实数V0>0 使得V(x)≥V0.

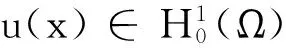
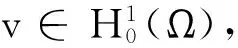
(2)

式中a(u,v)=(u,v)+(Vu,v).

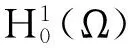
a(uh,vh)+(|uh|2uh,vh)=(f,vh),vh∈Sh.

(3)

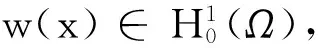
a(Phw,vh)=a(w,vh),∀vh∈Sh.

(4)

1　超收敛误差估计

引理1[6]若函数w(x)∈H2(Ω), 则其投影Phw(x) 有如下估计

‖w-Phw‖≤Ch2‖w‖2.

(5)

引理2[5]对任意函数v(x)∈Sh, 有如下逆不等式成立

‖v‖≤Ch-1‖v‖.

(6)

引理3设uh为 (3) 的解, 则有如下误差估计

‖uh‖≤C,‖uh‖≤C.

(7)

证明在 (3) 中取vh=uh, 有(uh,uh)+(Vuh,uh)+(|uh|2uh,uh)=(f,uh).由于 (uh,uh)≥0,(|uh|2uh,uh)≥0, 有

V0‖uh‖2≤(Vuh,uh)≤|(f,uh)|≤C‖f‖‖uh‖,

因此‖uh‖≤C‖f‖. 即式(7)的第一式得证. 另外, 由式(6)和式(5) 可得

‖uh-Phuh‖≤Ch-1‖uh-Phuh‖≤Ch‖uh‖2,

注意到‖uh‖≤‖Phuh‖+‖uh-Phuh‖, 得到‖uh‖≤‖Phuh‖+Ch‖uh‖2≤C. 因此, (7) 的第二式得证.

定理1设u和uh分别为式(2)和式(3)的解, 且u∈H2(Ω), 则有如下误差估计

‖uh-Phu‖≤Ch2,‖uh-Phu1‖≤Ch2.

(8)

证明由 (2)和(3)可得a(u-uh,vh)+(|u|2u-|uh|2uh,vh)=0,∀vh∈Sh.令u-uh=ρ-θ, 其中ρ=u-Phu,θ=uh-Phu, 则有

a(ρ-θ,vh)+(|uh|2(ρ-θ),vh)+((|u|2-|uh|2)u,vh)=0.

由 (4) 有a(ρ,vh)=0, 这样

a(θ,vh)+(|uh|2θ,vh)=(|uh|2ρ,vh)+((|u|2-|uh|2)u,vh),

取vh=θ有(θ,θ)+(Vθ,θ)+(|uh|2θ,θ)=(|uh|2ρ,θ)+((|u|2-|uh|2)u,θ).由于 (θ,θ)≥0,(|uh|2θ,θ)≥0, 则有

V0‖θ‖2≤(Vθ,θ)≤|(|uh|2ρ,θ)|+|((|u|2-|uh|2)u,θ)|,

因此V0‖θ‖≤‖|uh|2ρ‖+‖(|u|2-|uh|2)u‖.由 (5) 和 (7) 的第二式得 ‖|uh|2ρ‖≤‖uh‖‖ρ‖≤Ch2‖u‖2,另外

‖(|u|2-|uh|2)u‖≤‖u‖(‖u‖+‖uh‖)‖u-uh‖≤

‖u‖(‖u‖+‖uh‖)(Ch2‖u‖2+‖θ‖),

若记γ0=‖u‖(‖u‖+‖uh‖), 则得 (V0-γ0)‖θ‖≤Ch2‖u‖2. 假定γ0

即式(8) 的第一式得证, 类似可证明式(8)的第二式.

定理2设u和uh分别为式(2)和式(3)的解,uI∈Sh为u的双线性插值函数, 且u∈H3(Ω), 则有如下误差估计

‖uh-uI‖1≤Ch2.

(9)

证明[11] 中已经证得

(10)

2　数值实验

算例求解非线性薛定谔方程式(1), 其中Ω=[0,1]×[0,1], 势能函数V=1, 右端函数f(x) 选取其满足精确解为：

u=x(1-x)y(1-y)+ix(1-x)y2(1-y).

表1　数值结果

[1]陈传淼, 黄云清. 有限元高精度理论[M]. 长沙: 湖南科学技术出版社, 1995.

[2]林群, 严宁宁. 高效有限元构造与分析[M]. 保定: 河北大学出版社, 1996.

[3]WAHLBIN L B. Superconvergence in Galerkin finite element methods[M]. Berlin: Springer, 1995.

[4]HUANG Y Q, YANG W, YI N Y. A posteriori error estimate based on the explicit polynomial recovery[J]. Nat Sci J Xiangtan Univ, 2011, 33(3):1-12.

[5]AKRIVIS G D, DOUGALIS V A, KARAKASHIAN O A. On fully discrete Galerkin methods of second-order temporal accuracy for the nonlinear Schrödinger equation[J]. Numer Math, 1991, 59:31-53.

[6]JIN J C, WU X N.Convergence of a finite element scheme for the two-dimensional time-dependent Schrödinger equation in a long strip[J]. J Comput Appl Math, 2010, 234(3): 777-793.

[7]KARAKASHIAN O, MAKRIDAKIS C. A space-time finite element method for the nonlinear Schrödinger equation: the continuous Galerkin method[J]. SIAM J Numer Anal, 1999, 36(6):1779-1807.

[8]LU W Y, HUANG Y Q, LIU H L. Mass preserving discontinuous Galerkin methods for Schrödinger equations[J]. J Comput Phys, 2015, 282:210-226.

[9]WANG J Y, HUANG Y Q. Fully discrete Galerkin finite element method for the cubic nonlinear Schrödinger equation[J]. Numer Math Theor Meth Appl, 2017, 10(3):670-687.

[10]LIN Q, LIU X Q. Global superconvergence estimates of finite element method for Schrödinger equation[J]. J Comput Math, 1998, 16(6):521-526.

[11]TIAN Z K, CHEN Y P, WANG J Y. Superconvergence analysis of bilinear finite element for the nonlinear Schrödinger equation on the rectangular mesh[J]. Adv Appl Math Mech, 2018, 10(2):468-484.

[12]WANG J Y, HUANG Y Q, TIAN Z K, et al. Superconvergence analysis of finite element method for the time-dependent Schrödinger equation[J]. Comput Math Appl, 2016, 71:1960-1972.