钛合金点阵夹芯结构弯曲性能
2018-04-20王晓东苏亚东关志东
张 弥,王晓东,苏亚东,关志东
钛合金点阵夹芯结构弯曲性能
张 弥1,王晓东1,苏亚东2,关志东1
(1. 北京航空航天大学 航空科学与工程学院,北京 100191;2. 沈阳飞机设计研究所,沈阳 110035)
通过理论、试验、数值模拟3种方法研究3D打印钛合金金字塔型点阵夹芯结构在两端简支三点弯曲载荷下的响应,试验中通过裂纹观测仪监测加载过程。结果表明:在弯曲载荷下,夹芯结构损伤区域主要在弯矩最大中线处附近;试件首先在上面板出现塑性变形,随着第一层杆件的屈曲,载荷迅速下降。通过扫描电子显微镜(SEM)观测断口形貌,验证面板及杆件均为弯曲变形失效。基于ABAQUS软件,建立结点刚硬点阵夹芯结构有限元模型,对结构的渐进损伤过程进行预测,获得损伤起始位置、损伤扩展、破坏载荷及最终破坏模式等结果,模拟结果与试验结果吻合较好。通过有限元模型分析宽度方向不同单胞列数的影响,结果表明列数越多,边界影响越小,结构承载能力越强。
点阵夹芯结构;弯曲性能;渐进损伤;有限元模拟
点阵夹芯结构因其轻质高强、吸热、抗冲击等特点得到了国内外学者和工业界的青睐[1−3]。点阵夹芯结构的力学性能取决于芯子杆件的拉伸特征,结构的刚度和强度正比于材料的相对密度[4]。DESHPANDE 等[5]对理想铰接的硅铝合金材料点阵夹芯结构进行了弯曲试验,并建立了损伤机制图,结果表明,相比与金属泡沫夹芯结构,点阵夹芯结构质量明显下降;TAGARIELLI等[6]对不同边界条件下的复合材料点阵夹芯结构进行了弯曲试验,结果表明,简支梁表现出较柔软的后屈曲响应,而固支梁则较刚硬;ZOK等[7−8]以弯曲性能为优化目标对金字塔型点阵夹芯结构进行了优化设计,并通过理论和有限元方法预报了金字塔夹芯结构的等效模量;钱海峰等[9]研究了一种增强金属材料桁架夹芯复合壳板结构的压缩性能,结果表明,金属杆件发生塑性屈服并在中间部位出现断裂;YAN等[10]对比了金属点阵夹芯结构及泡沫填充瓦楞夹芯结构的弯曲性能,并建立了损伤机制图,结果表明,两者在冲击载荷下均可作为超轻结构的备选;YUAN等[11]研究了金属点阵结构在压缩载荷下的屈曲特性,结果表明,金属点阵结构的屈曲特性对局部损伤非常敏感。
3D打印技术是一种以数字模型文件为基础,运用粉末状金属或塑料等可粘合材料,通过逐层打印的方式来构造物体的技术[12]。它兼备数字制造、降维制造、堆积制造及快速制造的特点[13]。将3D打印应用于三维点阵夹芯结构的制造可降低制造的复杂度,节省原材料,且可获得结点刚硬连接的点阵结构。由3D打印技术制造的三维点阵夹芯结构的力学性能研究还未见发表。
本文作者针对3D打印钛合金金字塔型点阵夹芯结构,主要利用理论推导、试验及有限元手段,对其在两端简支下的三点弯曲性能进行研究。通过裂纹观测仪监测了加载过程中试件的渐进损伤及最终的破坏模式,并分析了点阵夹芯结构在弯曲载荷下的渐进损伤机理。建立了结点刚硬点阵夹芯结构有限元模型,分析点阵夹芯结构典型载荷点下的破坏模式,并探究了宽度方向单胞列数的影响,为以后研究3D打印点阵夹芯结构性能提供参考。
1 试验及理论分析
1.1 试验对象
本试验对象是3D打印钛合金金字塔型点阵夹芯结构。其材料性能、结构的单胞构型及尺寸如图 1所示,其厚度方向包含4层金字塔结构,每两层对称放置。试验件整体长度为207 mm,包含45列单胞,宽度为46 mm,包含10列单胞。
1.2 试验方法
两端简支三点弯曲试验参考试验标准ASTM C393/C393M−11在室温环境下进行。采用型号为HUNGTA HT2402的电子静力试验机(最大量程100 kN)进行位移控制方式加载,加载速度为2 mm/min。试验中的加载头和支座半径均为5 mm,跨距为150 mm。
试验过程中为精确捕捉试验现象,用相机及裂纹观测仪进行观测。同时通过摄像头将包含载荷位移数据及裂纹观测影像的电脑屏幕以每秒10帧的频率同步录制,典型录制结果如图 2所示,图2(a)所示为试验机记录的载荷位移曲线,图2(b)所示为对应时刻试验件的破坏模式。这种方式可以准确截取试验件在不同载荷点下的破坏模式,便于渐进损伤分析。
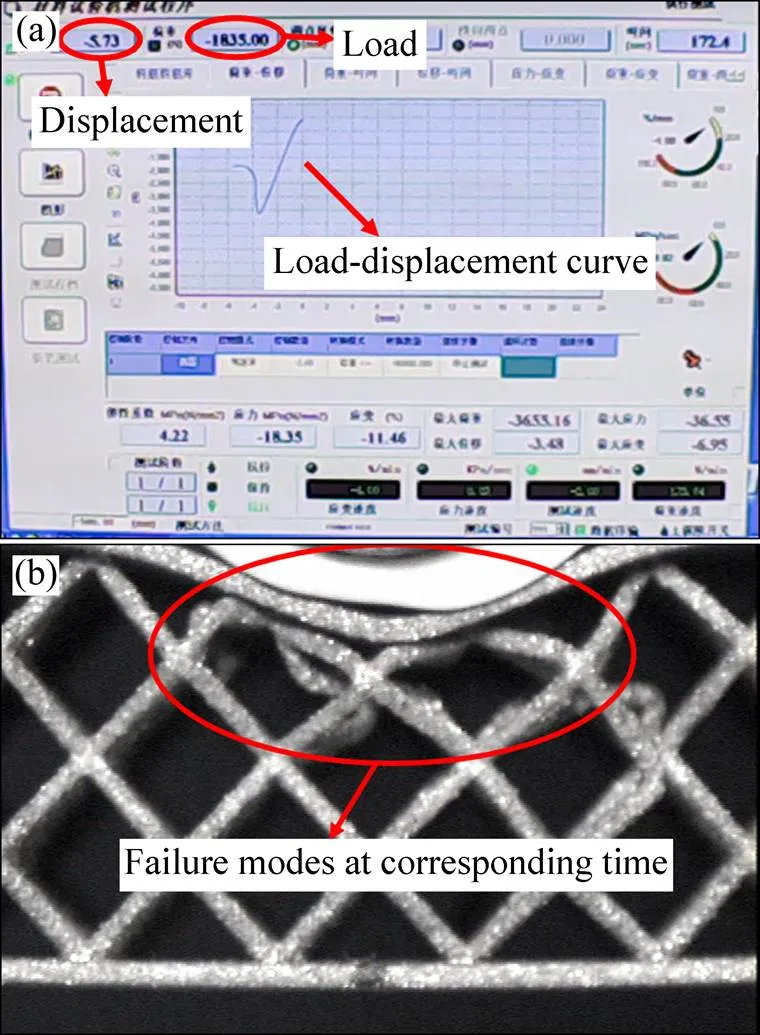
图2 载荷位移数据及同步观测影像示意图
1.3 理论推导及分析
由试验件单胞构型可知3D打印钛合金点阵夹芯结构的相对密度公式为
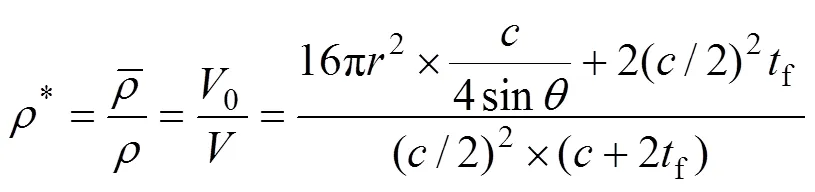
式中:0为夹芯结构单胞所占的实际体积,为夹芯结构所占空间立方体的体积,、、f、分别对应图中的尺寸,本研究点阵夹芯结构的相对密度为0.10867。
由于本研究的点阵夹芯结构的厚度相对于其长度和宽度来说是不可忽略的,因此整个夹芯结构在三点弯曲载荷作用下既要考虑弯曲变形又要考虑其横向剪切变形。对于这种金字塔型点阵夹芯结构,通常认为三点弯曲载荷作用下,弯矩由上下面板承担,剪力由点阵芯子承担[5],并考虑主要的两种破坏模式:面板破坏、芯子杆件破坏[14]。
面板破坏一般包含面板压溃、面板皱曲,压溃是由上面板所受压应力达到最大值而引起的,皱曲是由受压面板发生欧拉屈曲引起的。面板破坏其临界载荷为
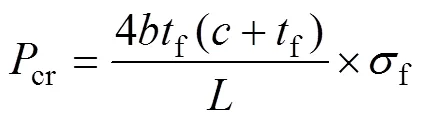
式中:f为面板强度,取面板压溃强度及皱曲强度的小者。即

式中:c为面板压溃强度,w为面板皱曲的临界应力。由夹芯结构尺寸,得出面板破坏下,结构对应的临界载荷cr=8.474 kN。
芯子杆件破坏一般包括杆件压溃、杆件屈曲。根据点阵结构构型,可以得到本研究金字塔形点阵杆件的临界载荷为
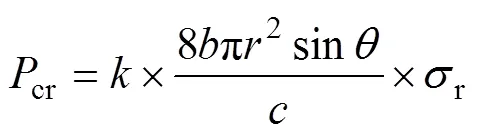
式中:为边界效应系数,根据本研究夹芯结构宽度方向特点,取0.9;r为杆件破坏强度。由本研究试件结构构型可知,杆件为中小柔度杆,采用抛物线形公式来计算其临界屈曲应力,因此

式中:m为杆件压溃强度,d为钛合金的极限强度,s为屈服强度。由夹芯结构尺寸,得出杆件破坏下,结构对应的临界载荷cr=3.896 kN。
结合以上理论推导,取结构对应临界载荷的最小值,可以得出3D打印钛合金点阵夹芯结构主要以杆件破坏为主,其理论计算破坏载荷为:cr=3.896 kN。
2 试验结果及分析
2.1 强度结果
参照ASTM C393中对于三点弯曲试验结果的计算公式可知,芯子的剪切强度为:
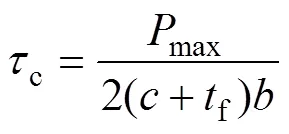
面板应力为:
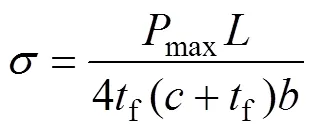
式中:max为最大弯曲载荷,为支撑跨距,、、、f对应图 1中单胞的尺寸。
试验得到最终破坏载荷为3.655 kN,计算得到芯子的剪切强度为4.07 MPa,此时面板的应力为545 MPa。
2.2 渐进损伤分析
3D打印钛合金金字塔型点阵夹芯结构的三点弯曲试验结果如图 3、图4所示。图 3所示为试验的载荷位移曲线;图4所示为载荷位移曲线上典型载荷点对应的破坏模式,、、、、、分别为20%峰值载荷、峰值载荷、第一层杆件屈曲载荷、第二层杆件屈曲载荷、二次峰值载荷及下降至20%峰值载荷点,这些载荷点揭示了试件的初始损伤及连续加载下的渐进损伤。
由试验结果及理论分析可知,加载头正下方是弯矩最大处,而三点弯曲试验的损伤也主要发生在试件中线附近长度方向的四列单胞内,本研究主要分析该区域内面板及杆件的渐进损伤。
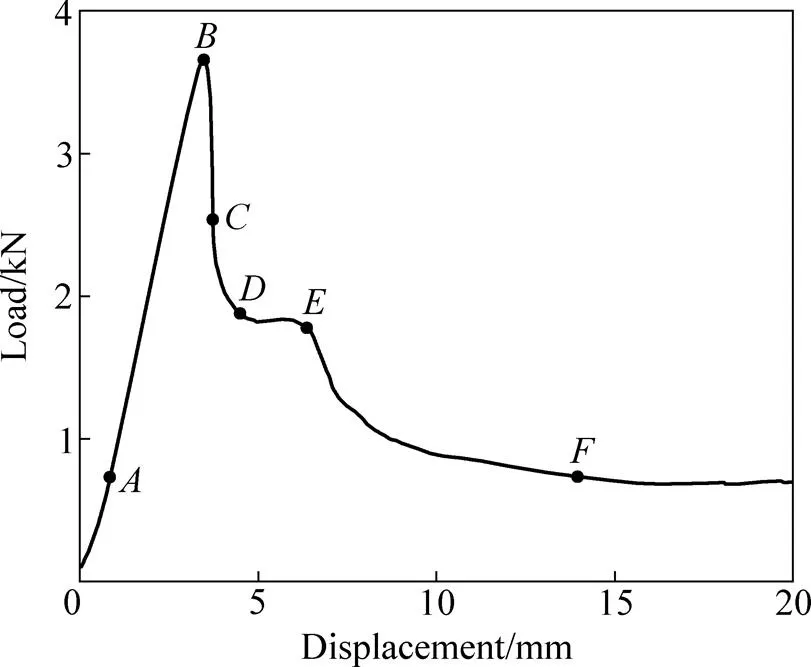
图3 三点弯曲试验载荷−位移曲线
由图3中点(约为峰值载荷20%)可知,加载头处在试验件的中线位置,试件长度方向单胞数量的布置致使加载头在两列结点中间,后续有限元模拟时也保证了其相对位置。在加载的初始阶段,随着位移的增加,载荷基本成线性增加,直到达到峰值载荷3.655 kN,对应位移达到3.476 mm,如图中点所示,此时,上面板出现塑性变形,面板内部杆件变形很小。随着位移的增加,上面板持续产生弯曲变形,载荷开始下降,且下降缓慢;随后,加载头下方附近两列结点处杆件发生明显屈曲,且载荷迅速下降,如图3中点所示。持续加载,加载头正下方第一层杆件几乎全部屈曲,且逐渐被压实如图3中点所示,同时第二层杆件也发生屈曲,载荷几乎处在平台期,此过程中杆件结点并无明显破坏。随着第二层杆件屈曲变形,载荷达到第二个峰值载荷,如图3中点所示;随着加载位移的持续增加,达到图3中点时,加载头正下方的前两层杆件均发生较严重的变形,此时位移达到13.96 mm。
结合试验载荷位移曲线及裂纹观测仪观测结果,可以看出结构第二峰值载荷1.78 kN约为第一峰值载荷3.655 kN的一半。这是由于第一峰值载荷为两列结点承力,而第二峰值载荷为一列结点承力。结果表明,多层结构使载荷位移曲线出现多个峰值,结构吸能能力突出。
2.3 SEM断口分析
通过扫描电子显微镜对破坏后的试验件断口进行破坏分析。
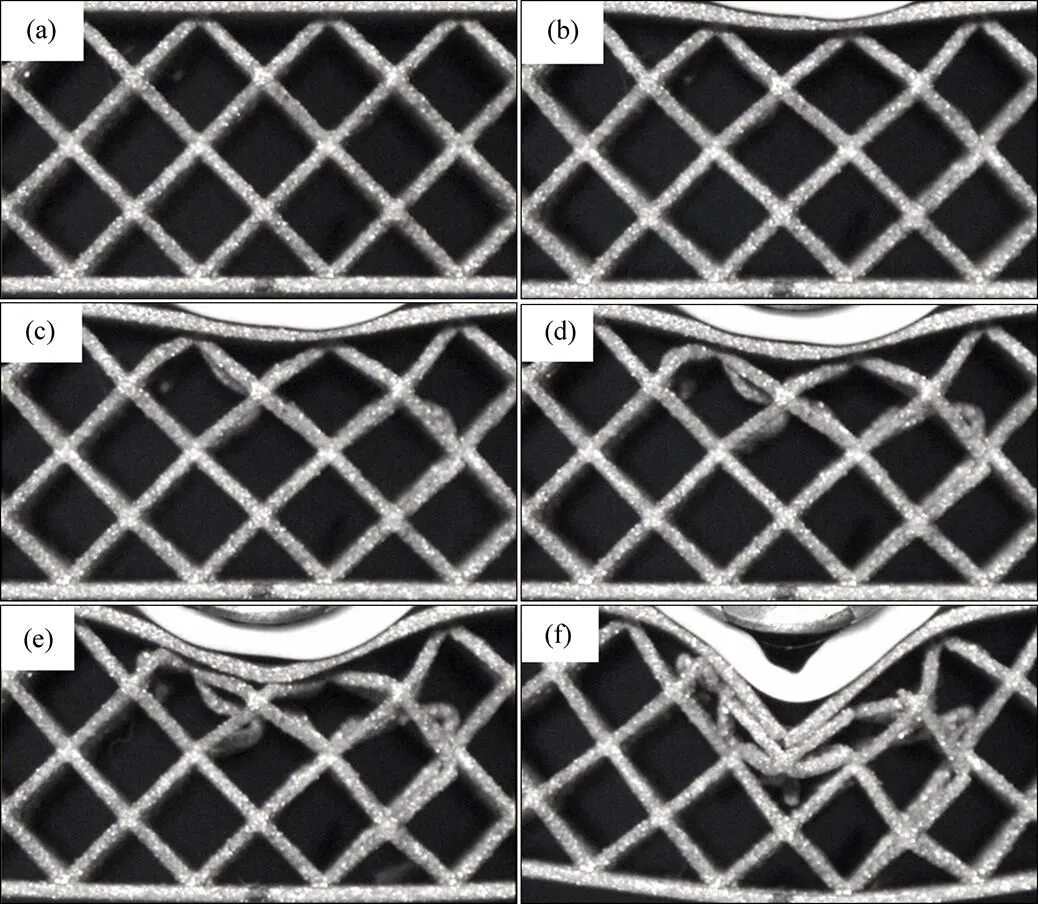
图4 不同时刻试件典型破坏影像
图5所示为面板断口形貌,从图中可以看出试件的断口包含两种不同的形貌,经放大后可以看出,颜色较亮部位比较粗糙,以等轴韧窝为主;颜色较暗部位比较光滑,以拉长韧窝为主。面板受弯曲载荷,受拉一侧(图中上侧)首先发生韧性破坏,产生等轴韧窝,当大部分面板破坏后,在面板压力作用下发生剪切破坏,产生拉长韧窝,直至整个面板断裂。
图6所示为杆件断口SEM形貌图,从图中仍可以看出断口包含两种形貌。杆件断口同样含有等轴韧窝区和拉长韧窝区,说明杆件也为弯曲失效。
2.4 有限元模拟
为进一步探究钛合金点阵夹芯结构在两端简支三点弯曲载荷下的破坏,本文通过有限元软件ABAQUS建立了钛合金点阵夹芯结构的三维有限元模型。由于本试验件是通过3D打印技术制造的,杆件之间的结点及杆件与面板之间的结点可以看作刚硬结点,因此有限元模型将面板与杆件建立成一个部件。
模型的几何尺寸与试验中测得的尺寸保持一致,上下面板使用4节点壳单元S4R。值得注意的是,由于试验件的上下面板在受载过程中会承受杆件结点处的集中力载荷,因此,模型上下面板不能使用实体单元,否则会出现奇异点。
对于结构中芯子杆件的模拟,由于在在弯曲载荷下,芯子杆件中应力比较复杂的区域在杆件中部,结点处受力比较简单,且该模型在结点处几何结构十分不规则,不易划分网格,因此选用两结点线性梁单元B31来模拟芯子杆件。相对于实体单元,选用梁单元既可以有效的提高建模速度和计算速度,又可以得到比较精确地计算结果,还可以避免结点处网格划分的复杂性问题。
本研究采用显式算法进行计算,通过质量放大的方式来提高计算效率。模型的网格划分如图所示,整个夹芯结构模型含28800个梁单元以及22050个壳 单元。
2.5 钛合金材料仿真
本研究中钛合金点阵夹芯结构是通过3D打印技术制造的。材料无损相应由线性响应和塑性响应两部分组成,线性响应性能为弹性模量=110 GPa,泊松比=0.31,塑性响应性能参考文献[15]中TC4的性能。
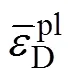

图5 面板断口形貌

图6 杆件断口形貌

图7 试验件有限元网格划分
定义
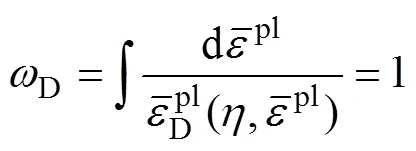
每一增量步中的计算公式为
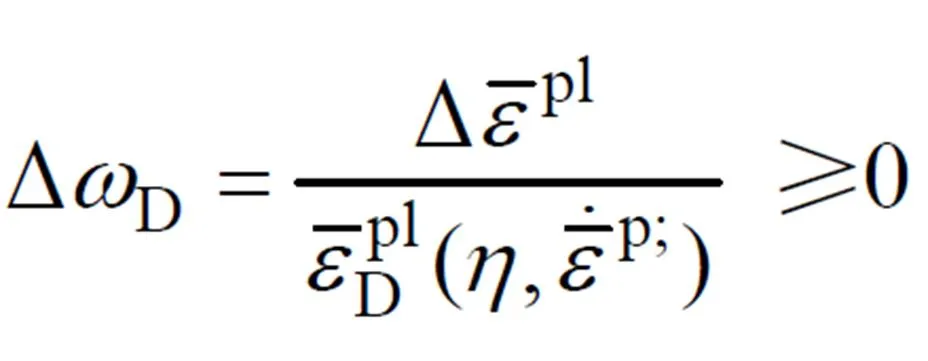
当状态变量达到D时,损伤起始。本研究的韧性破坏准则数据采用文献[16]中对TC4合金的研究结果。
2.6 边界及接触条件
为真实反应两端简支三点弯曲试验的加载,在有限元模型中建立了刚性体来模拟位移加载,其构型、尺寸与试验中的夹具保持一致。
模型中限制下端支座刚体3个方向的位移及转角,限制上端加载头刚体除加载方向外的其他两个方向的位移以及3个方向的转角;通过给定加载头加载方向的位移来模拟试验中的位移加载。
模型中采用通用接触来定义加载头、支座与试件之间的接触问题。
2.7 有限元结果分析
有限元计算的三点弯曲结果如图9所示,其中曲线2表示与试验件尺寸一致的计算结果,试验、理论、数值模拟结果的对比见表1。
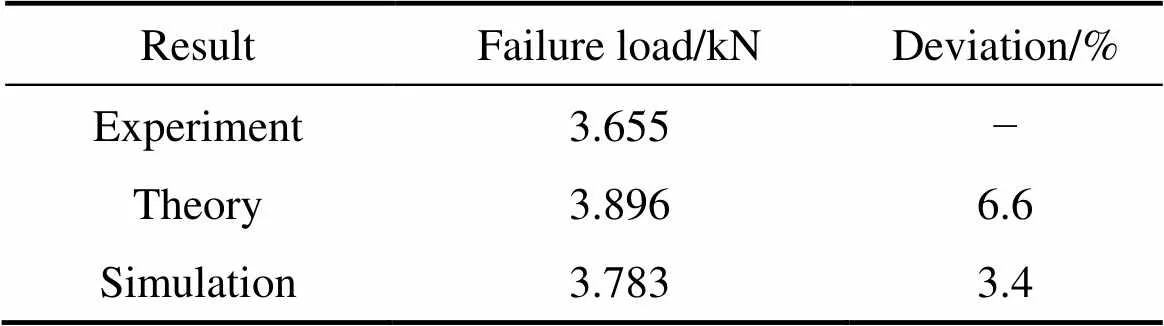
表1 结果对比
由表1可知,理论计算、数值模拟与试验结果误差在10%以内,吻合良好。
分析与试验结果中相对应载荷点、、、、、可知,有限元模拟结果中的破坏模式与试验保持一致。点阵夹芯结构上面板首先发生塑性变形,随后第一层杆件发生屈曲;且两次载荷下降,主要是由加载头正下方第一层与第二层杆件严重屈曲引起的。
相比于试验结果段的平台期,有限元模拟结果在第二层杆件承载时,载荷出现明显上升趋势,这是由于有限元计算是理想状态下的计算,夹芯结构所有杆件均处在理想完好状态,且结点连接绝对刚硬,在第一层杆件屈曲后,第二层杆件仍有较高的承载能力;而在实际试验件中,由于杆径较细,并非所有结点连接均完好,且有极少数的杆件在未试验前已发生折断,因此在第一层杆件发生屈曲时,有少量第二层杆件也出现屈曲。
通过定义有限元结果中结点的路径,可以直观得到杆件结点处应力沿宽度方向的分布。以加载头正下方杆件结点为例,其在最大载荷时刻沿宽度方向应力分布如图所示。由图8可知,结点处应力沿宽度方向分布较均匀,边界处结点为自由结点,缺少必要的约束,因此所承受的载荷较小,且沿宽度方向的影响较小。

图8 加载头正下方结点沿宽度方向应力分布
2.8 宽度尺寸的影响
为探究试件宽度对点阵结构弯曲性能的影响,有限元模拟分别计算了宽度方向含5列、10列、15列单胞的情况。由于试件仅单胞数量发生变化,构型未发生变化,因此相对密度保持不变。
有限元模拟的3种宽度的结果如图10及图10所示。3种宽度下强度结果数据见表2。
由模拟结果可知,在同样相对密度下,随着宽度方向单胞数量的增加,芯子剪切强度有小幅增加。
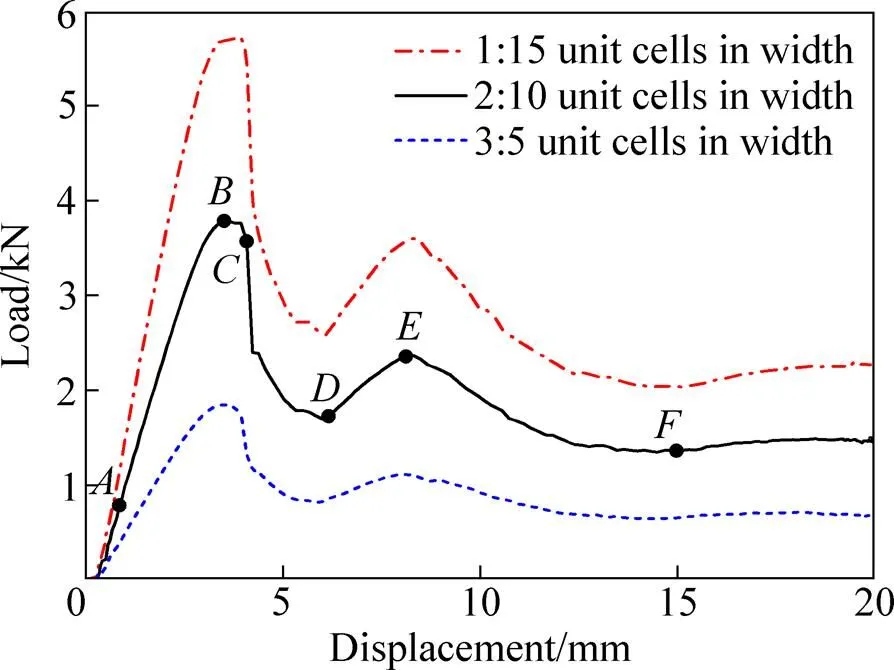
图9 不同宽度下载荷位移曲线

图10 宽度方向10列单胞试件应力云图
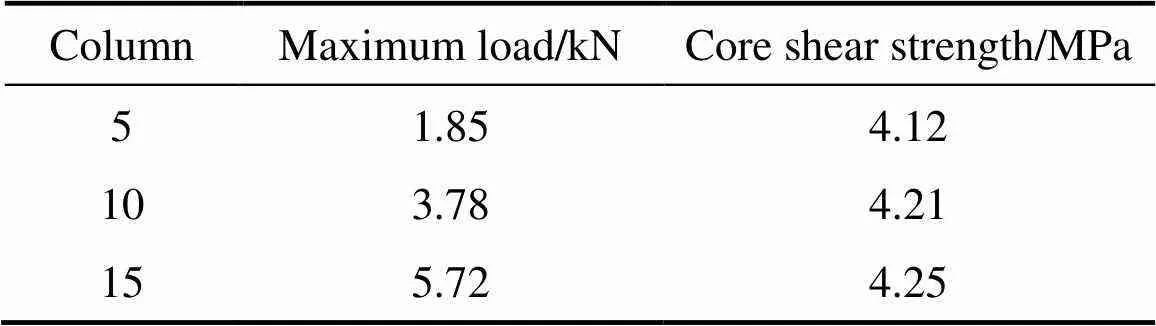
表2 不同宽度下强度结果
这是由于随着单胞宽度方向列数的增加,宽度两端边界所占的比例减小,边界的影响减小,因此结构的承载能力略有提高。
3 结论
1) 3D打印钛合金金字塔型点阵夹芯结构在两端简支三点弯曲载荷下,损伤区域主要在弯矩最大的试件中线长度方向的4列单胞内;
2) 两端简支三点弯曲载荷下,上面板首先发生塑性变形,随后第一层杆件发生屈曲,致使载荷迅速下降,结构失去主要承载能力,多层结构使载荷位移曲线出现多个峰值,结构吸能能力突出;
3) 随着宽度方向单胞列数的增加,夹芯结构的承载能力增强,是由宽度方向边界的影响减弱导致的;
4) 用梁单元模拟芯子杆件的有限元模型,可以有效地模拟3D打印点阵夹芯结构的弯曲性能,可推广到其他载荷及结构状态的有限元模拟。
[1] 方岱宁, 张一慧, 崔晓东. 轻质点阵材料力学与多功能设 计[M]. 北京: 科学出版社, 2009.
FANG Dai-ning, ZHANG Yi-hui, CUI Xiao-dong. Mechaninal properties and multifunctional design of lattice materials[M]. Beijing: Science Press, 2009.
[2] 曾 嵩, 朱 荣, 姜 炜, 蔡霄天, 刘金强. 金属点阵材料的研究进展[J]. 材料导报, 2012, 26(5): 18−23.
ZENG Song, ZHU Rong, JIANG Wei, CAI Xiao-tian, LIU Jin-qiang. Research progress of metal lattice materials[J]. Materials Review, 2012, 26(5): 18−23.
[3] 张钱城, 卢天健, 闻 婷. 轻质高强点阵金属材料的制备及其力学性能强化的研究进展[J]. 力学进展, 2010, 40(2): 157−169.
ZHANG Qian-cheng, LU Tian-jian, WEN Ting. Processes in the study on enhanced mechanical properties of high-performance lightweight lattice metallic materials[J]. Advances in Mechanics, 2010, 40(2): 157−169.
[4] WALLACH J C, GIBSON L J. Mechanical behavior of a three-dimensional truss material[J]. International Journal of Solids and Structures, 2001, 38(40): 7181−7196.
[5] DESHPANDE V S, FLECK N A. Collapse of truss core sandwich beams in 3-point bending[J]. International Journal of Solids and Structures, 2001, 38(36): 6275−6305.
[6] TAGARIELLI V L, FLECK N A, DESHPANDE V S. Collapse of clamped and simply supported composite sandwich beams in three-point bending[J]. Composites Part B: Engineering, 2004, 35(6): 523−534.
[7] ZOK F W, WALTNER S A, WEI Z, RATHBUN H J, MCMEEKING R M, EVANS A G. A protocol for characterizing the structural performance of metallic sandwich panels: application to pyramidal truss cores[J]. International Journal of Solids and Structures, 2004, 41(22): 6249−6271.
[8] ZOK F W, RATHBUN H J, WEI Z, EVANS A G. Design of metallic textile core sandwich panels[J]. International Journal of Solids and Structures, 2003, 40(21): 5707−5722.
[9] 钱海峰, 张振华, 牟金磊, 杜国宾. 金字塔点阵夹芯板单元结构准静态压缩性能研究[J]. 中国舰船研究, 2013, 8(5): 46−51.
QIAN Hai-feng, ZHANG Zhen-hua, MU Jin-lei, DU Guo-bin. Strength of sandwich structures with pyramidal lattice cores under quasi-static compressive loadings[J]. Chinese Journal of Ship Research, 2013, 8(5): 46−51.
[10] YAN L L, HAN B, YU B, CHEN C Q, ZHANG Q C.Three-point bending of sandwich beams with aluminum foam-filled corrugated cores[J]. Materials & Design, 2014, 60: 510−519.
[11] YUAN Wu, SONG Hong-wei, LU Ling-ling, HUANG Chen-guang. Effect of local damages on the buckling behaviour of pyramidal truss core sandwich panels[J]. Composite Structures, 2016, 149: 271−278.
[12] 李小丽, 马剑雄, 李 萍, 陈 琪, 周伟民. 3D 打印技术及应用趋势[J]. 自动化仪表, 2014, 35(1): 1−5.
LI Xiao-li, MA Jian-xiong, CHEN Qi, ZHOU Wei-min. 3D printing technology and its application trend[J]. Process Automation Instrumentation, 2014, 35(1): 1−5.
[13] 杨恩泉. 3D 打印技术对航空制造业发展的影响[J]. 航空科学技术, 2013 (1): 13−17.
YANG En-quan. The influence of 3D printing to the development of aviation manufacturing[J]. Aeronautical Science & Technology, 2013(1): 13−17.
[14] 王明亮. 复合材料金字塔点阵结构的 RTM 制备工艺及力学性能[D]. 哈尔滨: 哈尔滨工业大学, 2011.
WANG Ming-liang. RTM preparation technology and mechanical properties of composite pyramidal truss core sandwich structures[D]. Harbin: Harbin Institute of Technology, 2011.
[15] CHEN Guang, REN Cheng-zu, YANG Xiao-yong, JIN Xin-min, GUO Tao. Finite element simulation of high-speed machining of titanium alloy (Ti–6Al–4V) based on ductile failure model[J]. The International Journal of Advanced Manufacturing Technology, 2011, 56(9/12): 1027−1038.
[16] GIGLIO M, MANES A, VIGANÒ F. Ductile fracture locus of Ti-6Al-4V titanium alloy[J]. International Journal of Mechanical Sciences, 2012, 54(1): 121−135.
(编辑 何学锋)
Bending behavior of titanium truss core sandwich structure
ZHANG Mi1, WANG Xiao-dong1, SU Ya-dong2, GUAN Zhi-dong1
(1. School of Aeronautic Sciences and Engineering, Beihang University, Beijing 100191, China;2.Shenyang Institute of Aircraft Design, Shenyang 110035, China)
Response of 3D printing pyramid lattice structure under three-point bending were studied. Progressive damage during the loading process was detected with crack observation instrument. The results reflect that the main damage zone is in the middle of the specimen, where the maximum bending moment is located. The sudden drop of the load occurs with the buckling of the truss. The scanning electron microscope(SEM) is used to observe the fracture morphology which proves that the panels and trusses failed by bending. Finite element model with rigid nodes were established using ABAQUS. Damage location, damage propagation, peak load and failure modes are obtained, which corresponds with the test results. The effects of different unit numbers in width were investigated. It indicates that with more unit cells in width, the effects of the boundary are weakened, resulting in improvement of the load bearing capacity.
truss core sandwich structure; bending property; progressive damage; finite element simulation
2015-12-15;
2017-12-28
GUAN Zhi-dong; Tel: +86-10-82338873; E-mail: zdguan@buaa.edu.cn
10.19476/j.ysxb.1004.0609.2018.03.03
2015-12-15;
2017-12-28
关志东,教授,博士;电话:010-82338873;E-mail:zdguan@buaa.edu.cn
1004-0609(2018)-03-0457-08
V14.2
A
