基于HP滤波和ARIMA-ARCH模型的我国GDP分析与预测
2018-04-19冯长焕
王 丹,冯长焕
(1.2.西华师范大学数学与信息学院,四川南充,637000)
国内生产总值(GDP)指一个国家内所有常驻单位在一定时期内生产出的全部最终产品和劳务的价值总和,是衡量国家经济状况的一个重要指标。研究GDP有助于了解我国宏观经济的总体发展趋势和规律,掌握国家经济运行状况,对决策者制定正确的宏观经济政策具有重要指导意义。因此,不仅要掌握我国经济发展的总体趋势,还要掌握其波动性、周期性变化规律。
一、文献综述
众多学者对我国月度、季度、年度的国家或地区生产总值进行研究,利用的模型包含传统的单一模型和各种能优势互补以提高预测精度的组合模型。其中ARIMA模型因其简便易操作性的特点成为GDP研究中应用最为广泛的模型。[1-3]然而ARIMA模型对历史数据依赖性较强,预测步长短且不善于捕捉数据的非线性变化,因此常常利用一些改进的模型进行GDP分析与预测。赵喜仓对我国季度GDP序列建立SARIMA模型,预测相对误差较小。[4]何跃等利用成组织数据处理方法(GMDH)构建自组织模型,最终筛选出5个影响GDP变动的主要因素。[5]单玉隆建立改进遗传算法的优化神经网络模型,并与传统ARIMA模型进行比较,发现其GDP预测精度明显提高。[6]尹静、何跃对四川省GDP建立ARIMA、GMDH和ARIMA-GMDH模型,发现ARIMA-GMDH模型能有效提高预测精度。[7]吴齐、扬桂元、戚琦运用HP滤波技术将我国GDP年度数据做分解处理并展开宏观描述性分析,建立ARIMA模型进行分析与预测。[8]
然而,目前没有文献对分解得到的波动序列和趋势序列进行更深入的统计分析。我国GDP年度数据明显呈现出长期增长趋势和不同幅度的短期波动,因此本文首先采用HP滤波方法对我国GDP年度数据进行分解,再分别对分解得到的两组时间序列数据建立模型进行分析和预测,最终利用两组序列的预测序列对我国GDP年度数据进行分析与预测。
二、研究方法与模型
(一)HP滤波方法
HP滤波方法是Hodrick和Prescott在1981年分析美国二战后经济景气时首次提出的一种滤波方法,它在宏观经济研究中有着广泛的应用。HP滤波假设时间序列包含趋势部分和波动成分则:


(二)ARIMA模型
差分自回归移动平均模型,简记ARIMA模型(Autoregressive Integrated Moving Average Modle),是由Box和Jenkins于20世纪70年代初提出的一种时间序列预测模型,又称为Box-Jenkins模型。
ARIMA( p, d, q)中AR表示自回归部分,MA表示移动平均部分。其中:p代表自回归的滞后阶数,即表示序列的当期值与前 p期值有关;q 代表移动平均的滞后阶数,即表示序列的当期值与前q 期的扰动项有关;d 为将原始时间序列转化为平稳序列所需的最少差分次数。当 d = 0 时,表示原始时间序列为平稳序列,没有进行差分处理,这时建立的模型称为自回归移动平均模型(ARMA模型);当 p = 0 时,此时建立的模型为移动平均模型(MA模型);当 q = 0 时,此时建立的模型称为自回归模型(AR模型)。ARIMA模型的一般表达式为:

(三)ARCH模型
Engle于1982年提出自回归条件异方差模型(Autoregressive Conditional Heteroskedasticity Model,ARCH模型),为波动率建模提供了一个系统框架。ARCH模型的思想基础是:时间序列的扰动序列是序列不相关的,但不是独立的;扰动序列的不独立性可以用前期值的简单二次函数来描述。其一般表达式为:

三、实证分析
(一)HP滤波对数据的分解
由于我国在改革开放后社会经济发生了巨大变化,1978年以前的数据反应的经济变化与当今经济局势下的经济数据波动相差甚远。因此,选取东方财富网目前已共公布的我国1978—2016年的GDP(单位:亿元)年度数据进行分析。选取平滑参数分别为=100、= 6.25的两种滤波器对原始序列进行分解,结果如图1-3所示:
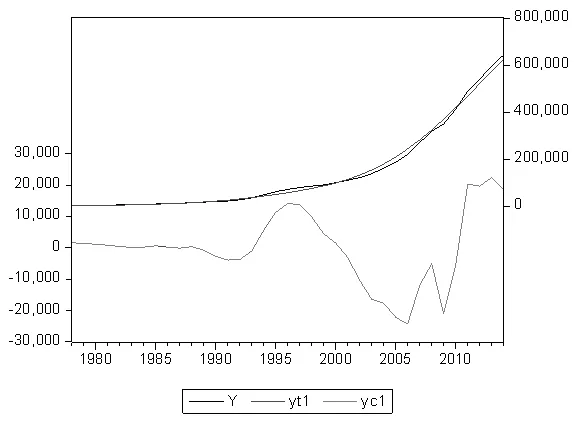
图1 =100

图2 = 6.25

图3 两种滤波器所得循环序列的时序
1997年受亚洲金融海啸影响,我国GDP呈现出波动性下降的趋势,国家积极采取策略应对危机,2006年后GDP发生明显的大幅度上升。2008年受全球经济危机影响,我国GDP又出现明显的大幅下落,到2009年跌入谷底,之后开始反弹。2011年受金融危机与欧债危机的影响,我国GDP再次出现下降,直到2014年依然没有明显的回升。比较图1、图2可以看出,当=6.25时,趋势序列与原序列几乎重合,趋势序列的跟踪程度更高。由图3看可以看出,当=6.25时,波动序列的振幅更小,波动规律与我国实际经济发展变化规律更加吻合。因此最终选择=6.25时的滤波结果进行进一步研究。
(二)模型的建立与预测
1.循环序列建模
由YC序列的时序图(见图4)可以看出循环序列虽有波动但不具有明显的线性趋势,序列可能是平稳的。一般采用ADF单位根检验法进行平稳性检验。由图4可以看出循环序列不存在截距项和明显趋势,因此选择不带截距项和趋势项的单位根检验。循环序列的ADF统计量为-6.579459,小于1%显著性水平的临界值,因此循环序列YC在1%显著性水平上是平稳的,可以继续进行建模。

图4 循环序列YC的时序图
循环序列的相关函数图如图5所示。可知循环序列的自相关函数是截尾的,偏相关函数衰减缓慢是拖尾的,因此应建立移动平均模型。

图5 YC的相关函数图
根据系数显著性、AIC准则、SC准则进行比较,最终得到最优模型为MA(3)模型,其系数估计值、标准误差、T统计值、系数显著性如表1所示:

表1 MA(3)模型参数拟合结果
模型表达式为:

对模型的残差序列进行检验,检验结果表明残差序列和残差平方序列都不存在序列相关性。这说明残差序列不存在ARCH效应,对循环序列建立的MA(3)模型能够有效的拟合真实数据。应用该模型对循环序列YC进行拟合和预测得到预测的循环序列YCF,预测效果如图6所示:

图6 模型预测效果图
2.趋势序列的建模与预测
为了提高预测精度,将循环序列的预测误差加入趋势序列中,即由YT1=Y-YCF得到新的趋势序列继续进行建模。得新的趋势序列YT1,其时序图如图7所示:

图7 新循环序列YT1的时序图
由图7可知,趋势序列YT1具有明显的非线性长期趋势,要先将序列平稳化处理。数据平稳化处理一般采用差分法,然而该序列即使进行两次差分后依然不平稳。为了避免过度差分造成过大的信息损失,先进行对数变换得到LYT1序列,再进行差分变换得到平稳序列DLYT1。进行ADF检验,结果显示ADF统计量为-3.083305,小于5%显著性水平临界值,说明DDLYT1序列在5%显著性水平下是平稳的。可继续对DLYT1序列进行建模。序列平稳化后对序列DLYT进行相关性检验,结果如图8所示:

图8 新循环序列的相关函数
可以看出,新循环序列的自相关函数衰减缓慢,是拖尾的,偏相关函数是截尾的。因此建立AR模型,通过AIC准则和SC准则进一步确定最优模型为AR(1)模型。建立AR(1)模型后对模型进行检验,发现模型的残差平方序列图存在明显的拖尾现象,说明残差序列可能存在ARCH效应。为了准确的检验出残差序列的ARCH效应,对残差序列进行LM检验。当滞后阶数为1时,残差序列的F统计量和LM统计量的显著性概率分别为0.0001、0.0002,都小于0.01显著性水平,故认为残差序列具有异方差性。对循环序列进行ARMA-ARCH建模,根据系数显著性、AIC准则、SC准则进行比较,最终确定AR(1)-ARCH(1)模型,结果如表2所示:

表2 AR(1)-ARCH(1)模型参数拟合结果
由表2可知,各参数在0.01的显著性水平上都是显著的,因此认为该模型合理。其表达式为:


3.原序列预测效果分析
通过对循环序列YC,新的趋势序列YT1进行建模与预测得到相应的预测序列YCF、YT1F。由于循环序列和趋势序列是由原序列HP滤波分解得到的,因此循环序列与趋势序列之和等于原序列即Y=YT+YC。预测序列有一定的不可避免的预测误差,不能由两个预测序列直接相加得到原序列的预测序列,通过线性组合得到的预测序列能较好的拟合原序列。利用循环序列的预测序列YCF、趋势序列的预测序列YT1F对原序列Y建立回归模型,得到的线性方程为:

对我国2015—2016年GDP的预测效果如图9所示。可以看出,预测序列与原序列拟合度较高。
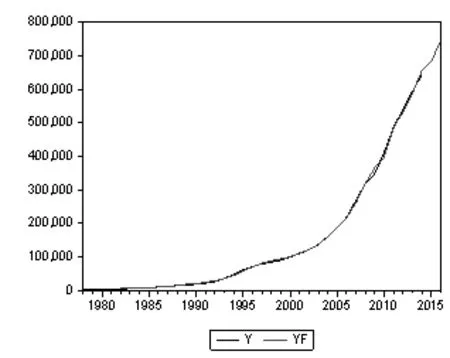
图9 GDP真实值与预测值对比图
为了比较模型的预测效果,对未分解的原始序列进行建模与预测并和本文预测结果进行对比,结果如表3所示。可以看出,本文的方法预测精度明显更高。

表3 改进方法前后预测精度对比
四、结论
将我国1978—2014年GDP作为原序列,采用改进的数据处理方法处理数据后再进行建模,并对我国2015年、2016年两年的GDP进行预测,与传统的不将序列分解而直接进行建模的预测方法进行比较,结果表明本文的建模方法可以提高最终预测精度,尤其是对常常出现高频波动性和周期性的经济数据,能更好地分析数据的波动性和趋势性。
参考文献:
[1] 周璇.基于时间序列分析的全国GDP预测模型[J].消费导刊,2009(13):76.
[2] 孙泗龙,李少博,范辰,等.基于ARIMA的GDP预测模型的构建及应用[J].辽宁科技大学报,2014,37(4):337-342.
[3] 冯瑞.GDP时间序列的ARIMA模型研究[J].重庆工商大学学报,2014(12):34-37.
[4] 赵喜仓.基于SARIMA模型的我国季度GDP时间序列分析与预测[J].统计与决策,2010(22):18-20.
[5] 何跃,鲍爱根,贺昌政.自组织建模方法和GDP增长模型研究[J].中国管理科学,2004,12(2) :139-142.
[6] 单玉隆.ARIMA模型与遗传算法优化神经网络在GDP预测中的应用[D].兰州大学,2014:7-13.
[7] 尹静,何跃.基于ARIMA-GMDH的GDP预测模型[J].统计与决策,2011(5):35-37.
[8] 吴齐,扬桂元,戚琦.基于HP滤波和ARIMA模型的我国GDP分析与预测[J].滁州学院学报,2015(5):35-38.
[9] Hodrick R J,Edward C.Prescott.Postwar U.S.Business Cycles:anEmpirical Investigation[J].Journal of Money,Credit,and Banking,1997,29(1).
[10] Ravn M O,Uhlig H.On Adjusting the Hodrick-Prescott Filter for the Frequency of Observations[J].The Review of Economics and Statistics,2002,84(2).
