基于无偏灰色马尔科夫模型的客流量预测
2018-04-19马彪
马彪
(铁道警察学院 轨道交通安全保卫系,河南 郑州 450053)
近年来,中国的城市轨道交通发展非常迅速,逐步成为市区人们日常出行的首选交通工具。截至2016年底,已获得国务院城市轨道交通建设项目批复的城市有58个,其中已经开通运营地铁的城市31个,预计到2020年将达到45个,未来5~10 a,我国城市轨道交通建设将进入高峰时期。对未来客流量的预测是影响轨道交通项目规划的一个重要指标,它为项目的决策与判断提供数据支持,同时也是后期运营中列车编组、行车密度和运行交路制定的重要参考依据。此外,随着各城市轨道交通的不断开通运营,公共安全问题也渐渐成为社会的热点话题,由于地铁处于地下密闭空间,具有联动性强、客流量大、救援困难等特点,一旦发生公共安全问题极易造成人员拥挤踩踏,后果不堪设想。虽然已开通城市轨道交通的城市都已组建了专门安保力量,但都面临警力不足问题。精确的客流预测能为公安机关科学灵活地用警布警提供科学依据,实现警力资源优化配置,确保城市轨道交通运营安全。
目前关于客流预测的方法和算法有很多种,国外有关学者在此方面做了大量研究,文献[1]提出目标导向神经网络预测模型,对公路短时客流进行预测,得到较好的预测效果。文献[2]结合贝叶斯规则和条件概率理论对不同的神经网络进行优化,将优化后的模型应用到高速公路短时客流预测,表明优化后的模型比单个神经网络模型的预测结果更准确。目前国内在客流预测方面正处于发展时期,文献[3]利用小波神经网络模型代替传统的BP神经网络模型对分解后的低频信号进行预测,精度有所提高。文献[4-7]运用灰色理论对城市轨道交通客流、铁路客流及铁路货运量进行预测研究。文献[8]在GM(1,1)模型的基础上改进了马尔科夫算法对城市轨道交通客流的周期时变特点进行研究。文献[9-10]运用灰色马尔科夫模型对铁路货运量和机场危险品数量进行预测。文献[11-15]对城市轨道交通客流预测技术、方法和模型进行研究。文献[16-18]对城市轨道交通客流特征进行分析研究。
综合客流预测的国内外研究现状可以发现:很多研究者都是针对长期客流预测进行研究,而对于短期客流预测,由于受更多因素的随机影响,呈现出更强的非线性和波动性,规律性很难把握,预测难度远超长期客流。本文以郑州地铁1#线为研究对象,重点对城市轨道交通短时客流的预测方法进行研究,以得到更加符合实际情况的城市轨道交通短期客流预测结果。
1 灰色GM(1,1)模型与无偏灰色GM(1,1)模型
1.1 灰色GM(1,1)模型
灰色理论是通过少量的、不完整的信息,建立灰色预测模型,对事物发展趋势做出模糊描述。城市轨道交通是一个抽象的系统,影响客流量的因素很多,如天气、节日、重大活动等,其中部分因素可知,部分因素未知,因此可将城市轨道交通系统看成一个灰色系统,进行客流预测常采用GM(1,1)模型。
GM(1,1)模型是一种最常用的灰色模型,表示一阶、单个变量的微分方程。设X(0)为非负的原始样本序列,即
X(0)={X(0)(1),X(0)(2),X(0)(3),……,X(0)(n)},
式中n为样本个数。
运用灰色理论对原始数据X(0)进行一次累加生成处理,得出新的生成序列X(1),有
新生成序列近似服从指数规律,对其建立预测模型,有
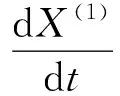
,
(1)
式中a、u为未知待定参数。
采用最小二乘法求解参数a、u,有
(2)

将a、u代入式(1)得出X(1)的灰色预测GM(1,1)模型
式中X(1)(k+1)为前(k+1) d的预测客流量累计之和。
累减还原后得到预测客流量
式中X(0)(k+1)为第k+1天预测客流量。
1.2 无偏灰色GM(1,1)模型
传统灰色GM(1,1)模型虽然计算简单,所用数据较少,但模型精度较低,存在偏差,为了提高精度,文献[18]提出无偏灰色GM(1,1)模型。与传统灰色GM(1,1)模型相比,无偏灰色GM(1,1)模型偏差减小,且无需累减还原,简化了建模步骤。无偏灰色GM(1,1)模型可表示为:
(3)
式中:b=ln((2-a)/(2+a)),A=2u/(2+a)。
由式(2)计算出a、u后,便可求得b、A,带入式(3)即可得出每日的预测客流量,不用进行累减还原,简化了计算步骤。
2 无偏灰色GM(1,1)模型检验
灰色GM(1,1)模型检验常用的有后验差检验和小误差概率检验。
2.1 后验差检验
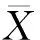
(4)
(5)

q(0)(k)=X(0)(k)-X^(0)(k),
(6)
(7)
(8)
计算后验差比值
C=S2/S1
。
(9)
2.2 小误差概率检验
(10)
一般情况下,模型的精确度等级划分如表1所示。

表1 模型检验等级表
3 马尔科夫模型
对于一个随机的过程,不同时刻下的状态之间具有某种联系。马尔科夫模型根据状态之间的转移概率来描述动态随机过程的发展状况,转移概率反映各状态之间的联系。城市轨道交通客流量的变化具有随机波动的特性,而马尔科夫模型可以描述随机波动的特点,因此可以采用无偏灰色马尔科夫组合模型,既可以通过无偏灰色GM(1,1)模型对城市轨道交通客流总体趋势进行预测,又可以利用马尔科夫模型对客流的随机性进行预测,使最后得出的预测结果更加符合城市轨道交通客流实际。
时间、状态都是离散的马尔科夫过程称为马尔科夫链,马尔科夫链是随机过程X1,X2,X3,……的一个数列,这些变量所有可能的取值集合就称为马尔科夫链的“状态空间”,其中任一状态可表示为:
X(0)(n)=X(t)P(n-t),
式中:X(t)为初始时刻t的状态概率向量;X(n)为经过n-t个时刻后的状态概率向量;P为状态转移概率矩阵。
计算得出无偏灰色预测值后,对其进行马尔科夫优化。首先对预测结果进行状态划分,然后计算状态转移概率,构造状态转移矩阵,最后应用马尔科夫模型进行优化。
3.1 状态划分
状态划分以实际客流量与预测客流量的相对误差R(k)为标准,分析相对误差序列的特点,对其进行分类,划分出不同的状态,使得数据尽可能均匀地分布在各个状态。R(k)的计算公式为:
(11)
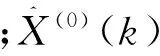
若将相对误差序列划分为m个状态,可表示为E1,E2,E3,……,Em,第i个状态区间Ei=[Qi,Ri],(i=1,2,……,m),其中Qi,Ri为状态Ei的上、下边界。
3.2 状态转移概率矩阵的构造
计算状态转移矩阵是马尔科夫模型的关键步骤,通过状态转移矩阵,可以清晰地看出各状态之间转移的概率,从而通过概率论方法确定下阶段客流量的走向,可以大大提高预测的精确度。分别计算每种状态向其他状态转移的概率,汇总得出状态转移矩阵。设状态Ei的数据个数为Mi,经过r步转移到状态Ej的数据个数为Mij(k),则状态转移概率
(12)
式中:i,j=1,2,……,m。
得到状态转移概率矩阵
3.3 马尔科夫优化

(13)
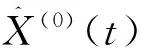
4 实例分析
4.1 选取样本
选取郑州地铁2017-02-03—02-18客流量数据(数据来源:郑州地铁运营公司)如表2所示。

表2 郑州地铁1#线客流量 万人·次
由表2可知:由于春节假期刚过(2月3日为农历一月初七),返程客流不稳定,导致客流数据波动性较大,但总体呈现上升趋势;周六(2月11日、2月18日)、周日(2月12日)客流相对于工作日客流减少,周一(2月13日)客流增长幅度最大,基本体现了城市轨道交通的客流特性。
4.2 无偏灰色GM(1,1)模型预测客流量
将表2原始的数列进行一次累加,根据式(2)可以得出:
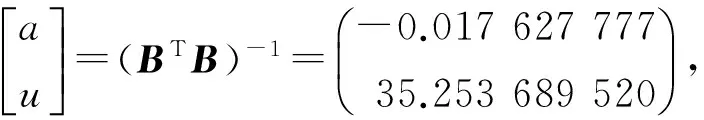
(14)

图1 无偏灰色预测客流量与实际客流量
通过式(14)得出2月3日至2月18日郑州地铁1#线无偏灰色预测客流量,并与原始数据进行拟合,结果如图1所示。
无偏灰色预测客流量虽然拟合了城市轨道交通客流的总体分布特征,呈指数增长趋势,但未能反映客流的随机性和波动性的变化特点,拟合效果较差。根据式(4)~(10)得出C=0.553 9,p=0.81,由表2可知,拟合精度为三级,勉强合格。
4.3 马尔科夫模型优化
根据式(11)计算R(k),并根据R(k)进行状态划分,共划分为4个区间,见表3。
根据式(13)及各状态区间的划分,对无偏灰色预测客流量进行马尔科夫优化,优化值与实际客流值进行拟合,如图2所示。
表3相对误差状态划分

状态编号状态区间日期一(-16%,-6%]4、8、18二(-6%,0]3、5、7、9、15三(0,4%]11、12、16、17四(4%,9%]6、10、13、14

图2 马尔科夫优化客流量与实际客流量
由图2可知:优化后马尔科夫预测与实际客流量拟合程度较高,同时能够反映客流的随机性和波动性,C=0.254 3,较无偏灰色预测量精度提高了54%,p=1,精度达到一级。
4.4 马尔科夫模型预测
根据式(12)和表3计算状态转移概率矩阵,分别得到2月16日、17日和18日的状态转移概率矩阵:
根据2月16日、17日和18日客流量及相应的状态转移概率矩阵P(1)、P(2)、P(3),对2月19日郑州地铁1#线客流量进行预测,其预测客流量最有可能处于的状态如表4所示。

表4 状态预测计算
通过表4可以看出,各状态下的状态转移概率的合计值状态二最大,表明通过状态转移,2月19日郑州地铁1#线的预测客流量最有可能处于状态二,即状态区间为(-6%,0],同理,对2月20日和21日郑州地铁1#线的客流量进行预测,结果见表5。
表52月19日至21日预测客流量
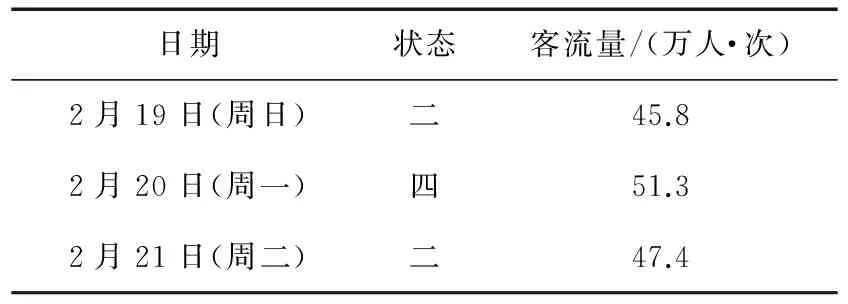
日期状态客流量/(万人·次)2月19日(周日)二45.82月20日(周一)四51.32月21日(周二)二47.4
可以看出,通过马尔科夫模型计算得出的预测客流量非常符合城市轨道交通客流的特点:周日客流较少,周一处于高峰期,周二相对于周一高峰期有所减少。由此判断,优化后的马尔科夫模型完全可以对城市轨道交通客流进行预测,效果较好。
5 结语
1)无偏灰色马尔科夫模型克服了无偏灰色GM(1,1)模型的缺点,既可以拟合城市轨道交通客流的总体发展趋势,又可以对随机性和波动性强的数据进行预测,模型精度较高,可以为地铁企业制定列车开行方案和公安机关布置警力提供依据。
2)构建马尔科夫模型过程中,不同的状态划分对最终预测结果的精度影响较大,因此如何进行科学合理的状态划分值得进一步研究。
参考文献:
[1]DIA H.An object-oriented neural network approach to short-term traffic forecasting[J].European Journal of Operation Research,2001,131(2):253-261.
[2]ZHENG Weizhong, LEE D H,SHI Q.Short-term freeway traffic flow prediction bayesian combined neural network approach[J].Journal of Transportation Engineering,2011,132(2):114-121.
[3]丁肃然.基于小波神经网络模型的短时交通流低频数据的预测[J].技术与市场,2017,24(11):80-83.
DING Suran. Forecast decomposed low rate signal using wavelet neural network model[J].Technology and Market,2017,24(11):80-83.
[4]吴强,冯维绣,胡晓嘉.灰色预测法在城轨客流预测中的应用[J].城市轨道交通研究,2004,6(3):52-55.
WU Qiang,FENG Weixiu,HU Xiaojia.The application of the grey prediction on passenger flow in UMT[J].Urban Mass Transit, 2004,6(3):52-55.
[5]黄召杰,冯硕.灰色预测模型在铁路客流中的应用[J].交通科技与经济,2014,16(1):57-60.
HUANG Zhaojie,FENG Shuo.Grey forecasting model in the application of railway passenger flow prediction research[J].Technology & Economy in Areas of Communications, 2014,16(1):57-60.
[6]郭琼琼.基于灰色系统理论的铁路货运量预测研究[D].郑州:解放军信息工程大学,2008.
GUO Qiongqiong.Research into the rail freight forecasting by the grey systems theory[D].Zhengzhou:PLA Information Engineering University,2008.
[7]穆勇.无偏灰色GM(1,1)模型的直接建模法[J].系统工程与电子技术,2003,25(9):1094-1095.
MU Yong.A direct modeling method of the unbiased GM(1,1)[J].Systems Engineering and Electronics,2003,25(9): 1094-1095.
[8]王奕,徐瑞华.基于周期时变特点的城市轨道交通短期客流预测研究[J].城市轨道交通研究,2010,12(1):46-49.
WANG Yi,XU Ruihua.Forecast of short-term metro passenger flow based on the periodically varying characteristics[J].Urban Mass Transit, 2010,12(1):46-49.
[9]林晓言,陈有孝.基于灰色马尔科夫链改进方法的铁路货运量预测研究[J].铁道学报,2005(6):15-18.
LIN Xiaoyan,CHEN Youxiao. Study on railway freight volume forecast by the gray-markov chain method[J].Journal of the China Railway Society,2005(6):15-18.
[10]赵振武,麻建军.基于灰色马尔科夫模型的机场安检危险品数量预测[J].安全与环境学报,2017,17(1):51-53.
ZHAO Zhenwu,MA Jianjun.Prediction of the amount of dangerous goods to be inspected by the airport security department via the grey markov model[J].Journal of Safety and Environment,2017,17(1):51-53.
[11]吕利民,李吴,温辛妍,等.城市轨道交通短期客流预测方法[J].都市快轨交通,2015,28(2):21-25.
LYU Limin,LI Wu,WEN Xinyan,et al.Methods for forecasting short-term urban mass transit passenger flow[J].Urban Rapid Rail Transit,2015,28(2):21-25.
[12]包磊.城市轨道交通客流量实时预测模型[J].城市轨道交通研究,2017(5):104-111.
BAO Lei. Real-time forecast of passenger flow volume in urban rail transit[J].Urban Mass Transit, 2017(5):104-111.
[13]王玉萍.城市轨道交通客流预测与分析方法[D].西安:长安大学,2011.
WANG Yuping.Study on urban rail transit passenger forecast and analysis[D].Xi′an:Chang′an Univercity,2011.
[14]王雪梅,张宁,张云龙.城市轨道交通短时客流预测体系框架及关键技术[J].交通运输工程与信息学报,2013,11(2):107-113.
WANG Xuemei,ZHANG Ning,ZHANG Yunlong.Framework and key technologies of short term passenger flow forecast of urban rail transit[J].Journal of Transportation Engineering and Information,2013,11(2):107-113.
[15]康海燕.北京轨道交通客流预测模型的研究[J].铁道运输与经济,2000(12):21-23.
KANG Haiyan. Studying the passenger volume forecast for beijing urban track traffic[J].Railway Transport and Economy,2000(12):21-23.
[16]赵晓芳,童晓进.郑州地铁1号线客流时空分布特征分析[J].城市轨道交通研究,2017(8):75-79.
ZHAO Xiaofang,TONG Xiaojin. Characteristic analysis of temporal and spatial distributions of passengers on zhengzhou metro Line 1[J].Urban Mass Transit, 2017(8):75-79.
[17]沈丽萍,马莹,高世廉. 城市轨道交通客流分析[J].城市交通,2007,5(3):527-531.
SHEN Liping,MA Ying,GAO Shilian. Passenger flow analys is of urban rail transit systems[J].Urban Transport of China,2007,5(3):527-531.
[18]张成.城市轨道交通客流特征分析[D].成都:西南交通大学,2006.
ZHANG Cheng.Analysis on the characteristics of urban rail transit passenger flow[D].Chengdu:Southwest Jiaotong University,2006.
