基于Optistruct的动力电池包振动分析

刘家员 ，王可洲,周伟

(1.澳汰尔工程软件(上海)有限公司 项目咨询部，上海　200436；2.山东农业工程学院 机械与电子工程学院，山东 济南　250100；3.中国重型汽车集团有限公司 业务部，山东 济南　250000)

随着全球能源危机的不断加深，石油资源的日趋枯竭以及大气污染的加剧，节能和减排是未来汽车技术发展的主要方向，发展电动汽车将是解决这两个技术难点的最佳途径。纯电动汽车完全由动力蓄电池提供电力驱动，针对目前蓄电池普遍存在价格高、寿命短等缺点，本文基于OptiStruct软件从某款电动汽车动力电池包的模态、随机振动、动刚度等方面进行分析，得到动力电池包的模态振型和随机振动应力以及不同频率下的振动情况，为电动汽车动力电池包的设计提供参考[1]。

1　电池包模态分析

汽车行驶过程中，当激励频率与其本身的固有频率相同时，便会产生共振，使乘坐舒适性降低。特别是汽车高速行驶时，车轮的动不平衡引起车轮激振，造成频率的增加，车速大于100 km/h时，车辆的振动频率约为15 Hz[2]。对电池包进行模态分析，找出各阶模态振型的频率，在结构设计时，使该频率避开该工况的振动频率，防止共振的发生。

1.1　分析基础

模态分析理论以假设线性、定常性与稳定性为前提，适用于结构的分析[3]。模态分析是振动分析最基础的部分，在有限元分析领域应用较多。由于汽车本身的复杂性，其振动由路面及轮胎、传动系统等许多激振源引起，振动分析时通常将汽车看成一个多自由度的弹性体系统[3]。将振动原理和有限元法相结合，组成线性多自由度系统，其微分方程为[4]：

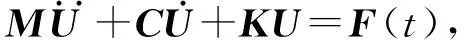
式中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；U为全局坐标系下的位移矢量；F(t)为总载荷矢量。

利用自由状态下的结构求解模型的模态，所以总载荷矢量F(t)=0。由振动理论可知，模态分析的两个物理量为固有频率和振型，在实际分析中阻尼的影响很小，所以在模态分析时，不考虑阻尼，其微分方程为

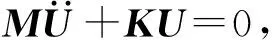
(1)

当激励源是简谐运动时，式(1)的解可写成

U=φsinωt

，

式中：φ为系统模态矢量；ω为系统固有频率。

则此条件下的特征方程为：

(K-Mω2)φ=0，

若保证方程中φ有非零解，则必须满足：

K-Mω2=0，

(2)

由式(2)可知，固有频率与电池包的质量和刚度有关，若电池包的质量已知，刚度由材料属性和物理属性决定，便可求得不同阶次的固有频率。

模态分析一般采用跟踪法、变换法、Lanczos法3种方法。有限元分析软件集成化中，选择Lanczos法的占大多数，其优势在于效率高，占用内存较少，并且支持稀疏矩阵，其相同坐标上可存放多个值，在现有的分析系统中占有很大的优势，本文基于Optistruct软件，采用Lanczos法进行模态分析。

1.2　分析结果

本文模拟装车的位置，即电池包的安装位置与实际汽车的安装位置保持一致，并约束沿x、y、z轴(x轴通过汽车质心且平行于汽车纵轴线指向汽车前进方向；y轴通过汽车质心垂直于x轴指向驾驶员侧；z轴通过汽车质心垂直指向上方)3个方向移动的自由度，对电池包做独立分析(忽略电池包的刚体模态)。电池包前8阶模态的计算结果如表1所示。其中第一阶模态固有频率为15.7 Hz，与车辆高速时的激振频率相差0.7 Hz，理论上可以避免共振，进一步研究可对电池包的支架和电池包的上下箱体进行优化处理。

表1　电池包前8阶固有频率及主振型特点

工程上的一阶频率很重要，而且常遇到结构的某一阶固有频率接近系统受到的外界激振频率，易发生共振。由工程实践可知，电池包的低阶固有频率为1～33 Hz，本次分析将重点放在低阶频率段，取电池包的1～4阶模态分析。

由表1可知：电池包第1阶固有频率为15.7 Hz，稍大于车辆高速行驶时的激振频率15 Hz，理论上满足要求[5]，为保证其可靠性可进一步优化；电池包第4阶频率为38.5 Hz，较前3阶频率波动较大，但1～4阶模态的固有频率基本为1～33 Hz，可考虑进行适当的优化。对电池包的优化，既要使其避免共振，又要满足轻量化的要求。

电池包1～4阶模态云图如图1所示(图中数值为位移的相对值)。由图1可知,振动最强的位置为上端盖和两边的支撑处，为优化的重点位置。

2　电池包的随机振动

2.1　电池包的随机振动理论

电池包的随机振动分析往往是为了确定结构的响应结果，通常是得到结构的位移、力以及应力的标准方差，通过分析得到其发生破坏的概率，为分析结构的耐久性提供基础。

a)第1阶　　　　　　　　　　　　　　　　　　　　　　　　b)第2阶

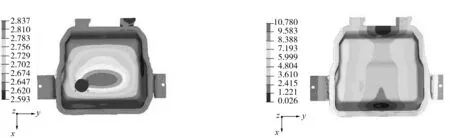
c)第3阶　　　　　　　　　　　　　　　　　　　　　　　　d)第4阶图1　电池包模态振型图

以模态分析得到的电池包固有频率和振型为基础[6]，通过对动力电池包的x、y、z轴方向进行不同的激励，采用模态叠加法，实现线性随机振动分析。模态叠加法的整个运动方程采用解耦方式求解，优势在于求解速度较快，并且可以根据需要进行单个频率下求解，还可以设置比较集中的模态频率，方便客户需求，但是也有一定局限性，例如需要模态解的特征向量，只适应线性分析，不适合非线性求解,应力结果求解过程不理想。可以通过非比例阻尼求解器求解，但是对于定义了非比例阻尼求解量，则m个单自由度是通过阻尼矩阵相互耦合的，此时—般用QR阻尼法求解。

2.2　电池包随机振动分析

按照文献[7]的要求，将测试对象安装在振动试验台上，通过扫频方法进行测试，采用加速度方式加载，振动频率为5～200 Hz。z轴方向频率与功率谱的对照法规给出两种功率谱密度，如表2所示。

根据我国相关规定，做相同条件下的随机振动测试有限元分析。运用模态法进行仿真，仿真中主要用z向的单位激振力，求解得到加速度下的功率谱密度，并给出了新能源汽车电池包下端盖的动态最大随机振动应力，如图2所示(图中应力的单位为MPa)。

表2z轴方向的振动频率与功率谱密度

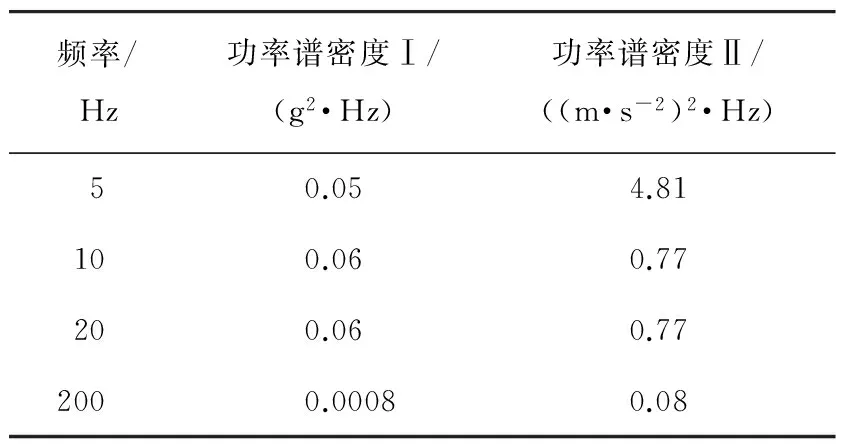
频率/Hz功率谱密度Ⅰ/(g2·Hz)功率谱密度Ⅱ/((m·s-2)2·Hz)50.054.81100.060.77200.060.772000.00080.08

图2　下端盖应力云图

由图2可知，下端盖的最大应力为552.1 MPa，材料的抗拉极限应力为300 MPa，安全系数为0.53，不满足安全因数为1.25～2.5的要求，应对下端盖进行优化，提高其安全因子。

3　电池包的动刚度

动刚度是在不同频率的激励下，结构本身抵抗变形的能力。电池包的动刚度除与自身的物理性质有关外，更与激励源的振动有关。电池包与车架的连接点是振动输入的源头，必须首先考虑连接点输入的信号动态特性和安装点的动态特性[8]。电池包安装在白车身上，外界激励通过连接装置传递，若连接点的刚度过低必然影响隔振效果并引起更大的振动，不但会造成电池的破坏，还会对整车噪声、振动与声振粗糙度(Noise、Vibration、Harshness，NVH)性能有较大的影响。本文对电池包与车架连接处的振动对动刚度的影响进行分析[9]。

3.1　电池包动刚度理论

安装点的振动对电池包的动刚度影响较大，主要分析电池包在不同频率下的振动情况，频率响应常用于分析线性结构一定频率范围内载荷变化时的稳态响应[10]，其类型分为位移、速度、加速度响应函数，进而得到频率响应曲线。电池包的动刚度采用加速度频率响应导纳进行评价[11]。

单点激励的频响函数引入原点(当响应点和激励点一致时为原点，这里可理解为连接点)动刚度的理论依据：假设对电池包某单点P(激励点) 进行激励，对单点L(响应点)进行响应分析[12]。

对于多自由度系统来说，由模态理论得振动响应公式[13-14]：

对应外界激励点P的第r阶模态对应的解为：

(3)

式中φpr为激励点P第r阶的振型系数。

物理坐标下测点L位移响应的频响函数为：

(4)

式中：φLr为响应点L的r阶振型系数，r=1,2，……，n。

将式(3)代入式(4)得：

位移与激振力之间的传递函数，亦即电池包P点到L点的结构传递函数为:

(5)

当响应点L与输入点P相同，也即原点就是响应点时，式(5)变为原点的结构传递函数，即

对于单自由度系统在单位简谐激振力作用下的振动系统运动方程简化为：

KXL=cosωt，

式中：K为参考刚度(设计目标)；XL为外界激励下的位移。

振动加速度与激振力的比值定义为加速度导纳的传递函数，有

(6)

式中f为频率。

由式(6)得

(7)

3.2　电池包动刚度分析

图3　标准刚度与不同动刚度下的加速度曲线

依照实际工程经验， 拟合目标刚度为10 kN/m的标准加速度频率响应包络线[15](用对数函数拟合)。依据式(7)，刚度K=10 kN/m，频率f在一定范围内变化时，加速度的变化曲线如图3所示。

利用Optistruct求解器进行求解，电池包的边界条件与实车约束一致，对z方向施加单位载荷的集中力[16]，频率范围为0～220 Hz，步长为1 Hz，结构阻尼为0.04，以激励点作为响应点，输出z轴激励的加速度曲线如图3所示。

正常情况下，模拟出的加速度响应曲线应在标准加速度响应曲线之内或者处于贴合状态。从图3中可以看出，标准加速度响应曲线与模拟的加速度响应曲线贴合度较高，在0～60 Hz段稍微高于标准值，原因是电池包与车体分开而作为一个独立体进行仿真，可能存在一定的误差[17]。

计算得0～220 Hz的平均动刚度为14.97 kN/m，明显高出标准值10 kN/m，表明电池包的动刚度满足要求[18]。

4　结语

1)模态分析表明：第一阶模态频率为15.7 Hz，略高于高速行驶时的激振频率，理论上可以避免共振；进一步研究可对电池包的支架和电池包的上下盖做优化处理。

2)随机振动应力分布的结果，下端盖材料的安全系数明显较低，需要对电池包下端盖的结构做进一步优化处理。

3)电池包的局部动刚度基本满足要求，低频稍有出入，计算的平均动刚度为14.97 kN/m，超过标准值10 kN/m，认为电池包不会因外界的激励产生破坏，所以在后续的优化中，不再将动刚度作为优化的目标。

参考文献：

[1]DONG B, GOETCHIUS G M, DUNCAN A E. Process to achieve NVH goals: subsystem targets via “digital prototype” simulations[C].Michigan:SAE Paper, 1999.

[2]成亚南, 史建鹏. 基于HyperWorks软件的发动机装饰罩振动特性分析[C]// Altair 2012 HyperWorks 技术大会论文集.上海：Altair 2012 HyperWorks 技术大会, 2012:1-2.

CHENG Yan′an, SHI Jianpeng. Engine cover decoration vibration characteristic analysis based on HyperWorks software[C] //Proceedings of Altair HyperWorks Technology Conference.Shanghai:Altair HyperWorks Technology Conference, 2012:1-6.

[3]胡旭. 电动汽车动力蓄电池箱有限元仿真及模态分析[D].长沙: 湖南大学, 2015.

HU Xu. Electric vehicle power battery box finite element simulation and modal analysis[D].Changsha:Hunan University, 2015.

[4]HE J, FU Z F. Local structural modification[J].Modal Analysis, 2001,8(2):224-240.

[5]AMATO E, DURANTE F. Distributed structural modification using local interface model[C].ISMA Belgium:International Conference on Noise and Vibration Engineering,2002.

[6]韩锋钢, 张思泉, 林有淮.某车用电池箱随机振动仿真分析[J].机电技术, 2016(4): 9-12.

HAN Fenggang, ZHANG Siquan, LIN Youhuai. A car battery box random vibration simulation analysis[J].Mechanical and Electrical Technology, 2016 (4) : 9-12.

[7]全国汽车标准化技术委员会.电动汽车用锂离子动力蓄电池包和系统:GB/T 31467.3—2015[S].北京：中国标准出版社, 2015.

[8]刘鸿文.材料力学[M].北京：高等教育出版社, 1985.

[9]邹途祥, 张军, 贾文宇.车身接附点动刚度的研究[C]//LMS 2013中国用户大会论文集. 上海：LMS2013中国用户技术大会，2013:5-6.

ZOU Tuxiang, ZHANG Jun, JIA Wenyu. Body by dotted dynamic stiffness research[C]//Proceedings of LMS 2013 Chinese Users Conference. ShangHai: LMS 2013 China User Technology Conference, 2013:5-6.

[10]许林.车身悬置支架的动刚度分析[J].农业使用与维修, 2011(3):24-26.

XU Lin.Analysis of dynamic stiffness about autombile body mount[J].Farm Machinery Using and Maintenance, 2011 (3) : 24-26.

[11]COGSWELL J A. Mechanical mobility relationship to the dynamic properties of the structure-borne vibration path within the power train and vehicle[C].Michigan：SAE 2003 Noise & Vibration Conference and Exhibition, 2003.

[12]王志亮,刘波,桑建兵,等.动刚度分析在汽车车身结构设计中的应用[J].机械设计与制造,2008(2): 30-31.

WANG Zhiliang, LIU Bo, SANG Jianbing,et al. Dynamic stiffness analysis in the application of body structure design[J].Mechanical Design and Manufacture, 2008 (2) : 30-31.

[13]倪振华.振动力学[M].西安:西安交通大学出版社,1988.

[14]FAHY F, KALNINS A. Sound and structural vibration radiation,transmission and response[J].Astrophysics, 2008, 108(4):373-374.

[15]PARK J. Influence of support viscoelastic properties on the structural wave propagation[J].Journal of Mechanical Science & Technology, 2007, 21(12):2117-2124.

[16]KIM K, CHOI L. Design optimization analysis of body attachment for NVH performance improvements[C].Detroit：SAE Noise & Vibration Conferece & Exhibition, 2003.

[17]张军, 方向明. 反共振频率的灵敏度分析及应用[J].振动工程学报, 1996,9(1):9-15.

ZHANG Jun, FANG Xiangming. Sensitivity analysis of structural anti-resonance of vibratory system[J].Journal of Vibration Engineering,1996, 9(1):9-15.

[18]JOHNSON E A, WOJTKIEWICZ S F. Efficient sensitivity analysis of structures with local modifications transfer functions and spectral densities[J].Journal of Engineering Mechanics, 2014, 140(9):0401-4068.