氧桥联希夫碱GdNi双核配合物磁学性质理论研究

范光鼎，罗树常, 2 ，殷 俊，李晓青，方春平

(1.贵州工程应用技术学院化学工程学院，贵州 毕节 551700;2.贵州省化学化工实验教学示范中心，贵州 毕节 551700)

自1864年发现席夫碱(Schiff碱)以来[1]，Schiff碱及其金属配合物因其具有特殊活性和极强的配位能力，在超氧化物歧化酶及生理活性、医学、催化、分子基磁性材料等领域有广泛的应用前景而备受关注[2-3]。由镧系金属离子与过渡金属离子通过有机桥联配体形成的3d-4f金属配合物具有优异的光、电、磁功能，它结合了4f金属离子高的自旋基态、大的负磁各向异性及3d过渡金属离子强的磁相互作用，在高密度信息存储磁性材料、量子计算机、多功能分子基磁体等领域有潜在的应用价值而引起科学家广泛关注[4-10]。本文以南开大学刘欣教授等[4]人用席夫碱配体、醋酸镍和硝酸钆合成的氧桥联希夫碱GdIIINiII双核配合物[Ni(HL)(H2O)(tfa)Gd(hfac)2]来研究顺磁中心GdIII和NiII间的磁交换作用机理，通过与实验值进行比较。以此来选择密度泛函理论结合对称性破损态方法(DFT-BS)计算氧桥联希夫碱GdNi双核配合物磁耦合常数的条件，以期为希夫碱GdIIINiII双核配合物磁学性质的研究提供一定理论参考。

1 计算方法及模型

1.1 计算模型

为考察DFT-BS方法下计算氧桥联希夫碱GdIIINiII双核配合物磁耦合常数时泛函、基组等因素对计算结果的影响，选取氧桥联希夫碱GdIIINiII双核配合物[Ni(HL)(H2O)(tfa)Gd(hfac)2]为计算模型，如图1所示。计算所用结构均来自X-射线单晶衍射数据，为作改动。

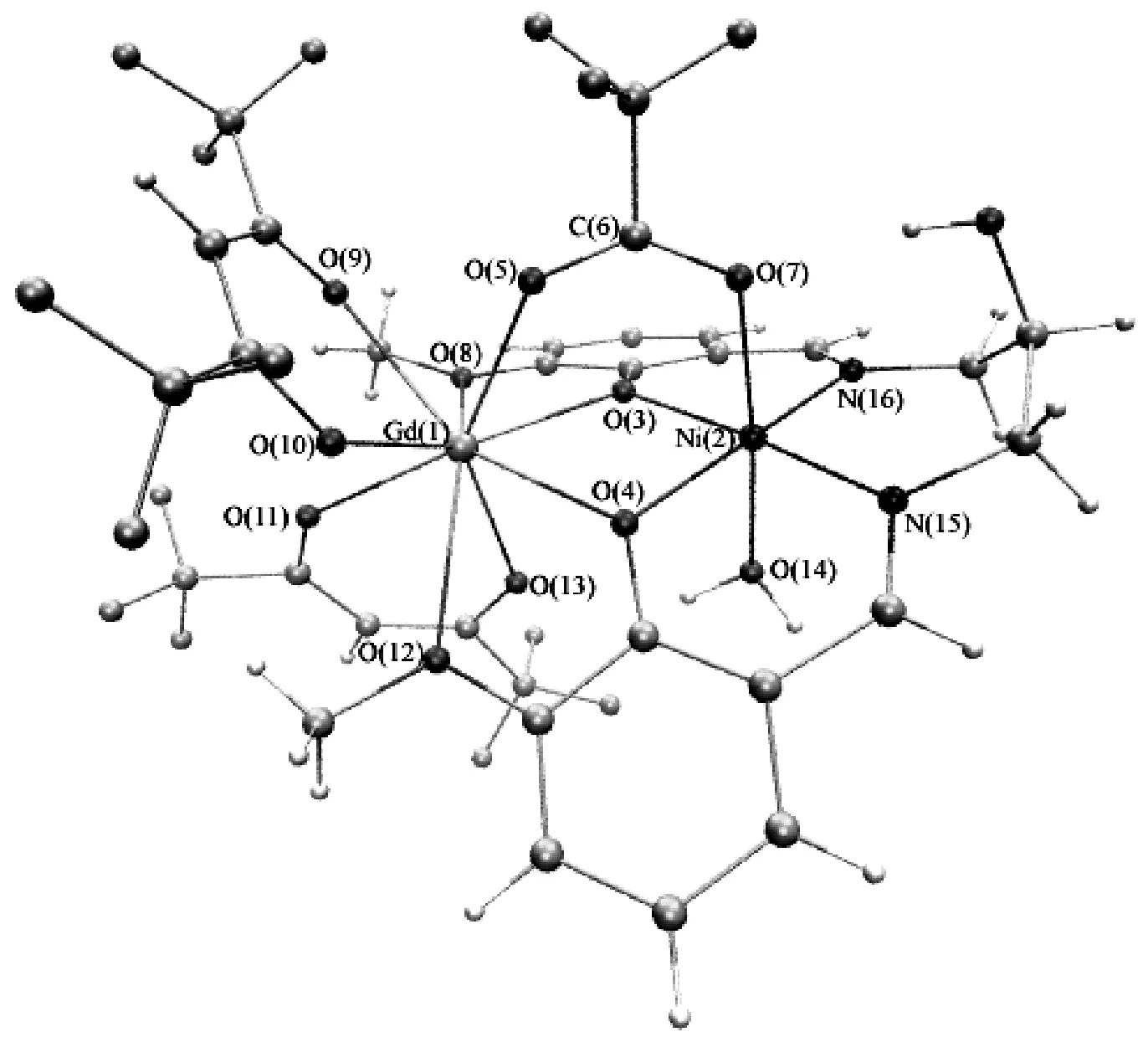
图1 氧桥联希夫碱GdIIINiII双核配合物[Ni(HL)(H2O)(tfa)Gd(hfac)2]结构

1.2 计算方法

顺磁中心GdIII和NiII间相互作用可用HDVV哈密顿量描述：

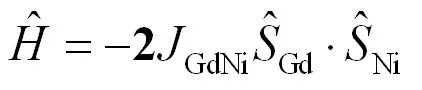
(1)

JGdNi表示顺磁中心GdIII和NiII间的磁耦合常数，它的符号和绝对值的大小表达了其磁耦合作用大小和强弱[10]。JGdNi>0，顺磁中心是铁磁性相互作用，JGdNi<0，则为反铁磁性相互作用[10]。

采用DFT-BS方法计算双核过渡金属配合物的磁耦合常数，计算公式为

(2)

所有计算使用 ORCA4.0.1 软件[11]在贵州工程应用技术学院化学工程学院计算化学实验室正睿I2TS2-8898HV 服务器上完成[10]， 所有图形用 VMD 1.9.2[12]显示[10]。

采用DFT-BS方法，选取2种局域密度近似方法、5种广义梯度近似方法、7种混合密度泛函方法和6种含动能密度的meta-GGA方法，选用TZVP(Gd为SARC2-DKH-QZVP)基组计算磁耦合常数Jcalc值，选取最好的一种泛函方法测试不同基组对磁耦合常数Jcalc值的影响。

2 结果与讨论

2.1 磁耦合常数J

表1为20种方法在TZVP(Gd为SARC2-DKH-QZVP)基组下计算的磁耦合常数Jcalc值。由表1可知，四类密度泛函方法计算的磁耦合常数均大于零，与实验测量结果Jexp =1.83 cm-1一致。2种局域密度近似方法(LDA和VWN3)计算的结果分别为2.25 cm-1至2.04 cm-1，与实验值的差值较大，主要是因为在密度泛函理论中局域密度近似最粗略。5种GGA泛函方法(PBE、BP86、BLYP、XLYP、PW91)计算的数值在1.51 cm-1至1.91 cm-1之间，极差仅有0.40 cm-1，其数字与实验值1.83 cm-1都比较接近，其中Perdew和 Wang于1992年提出的PW91方法计算的结果1.82 cm-1与实验值1.83 cm-1极其吻合。7种混合泛函方法(B3LYP、O3LYP、X3LYP、PBE0、B3P86、mPW1LYP、mPW1PW)计算的结果在1.17 cm-1至1.71 cm-1之间，极差为 0.54 cm-1，与实验值相差较大。6种meta-GGA泛函方法(M06、M06-L、M06-2X、TPSS、TPSS0、TPSSh)计算的结果在0.91 cm-1至2.00 cm-1之间，其极差达到了1.09 cm-1，与实验值1.83 cm-1相差较大。所以计算中选用PW91方法计算氧桥联希夫碱GdIIINiII双核配合物[Ni(HL)(H2O)(tfa)Gd(hfac)2]的磁耦合常数Jcalc值。

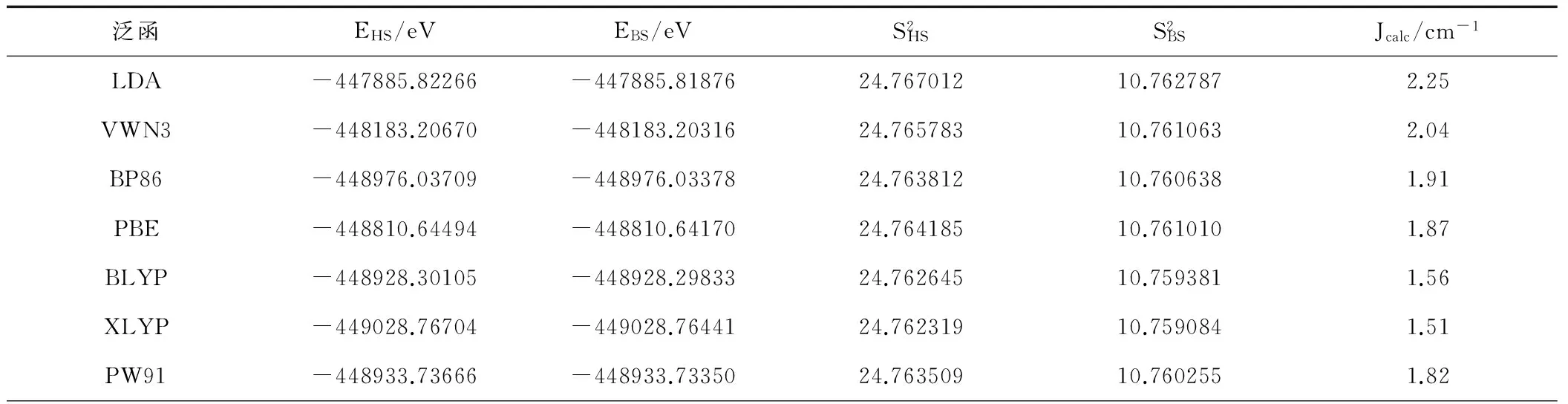
表1 TZVP(Gd为SARC2-DKH-QZVP)基组下不同泛函对磁耦合常数J的影响(Jexp=1.83 cm-1)

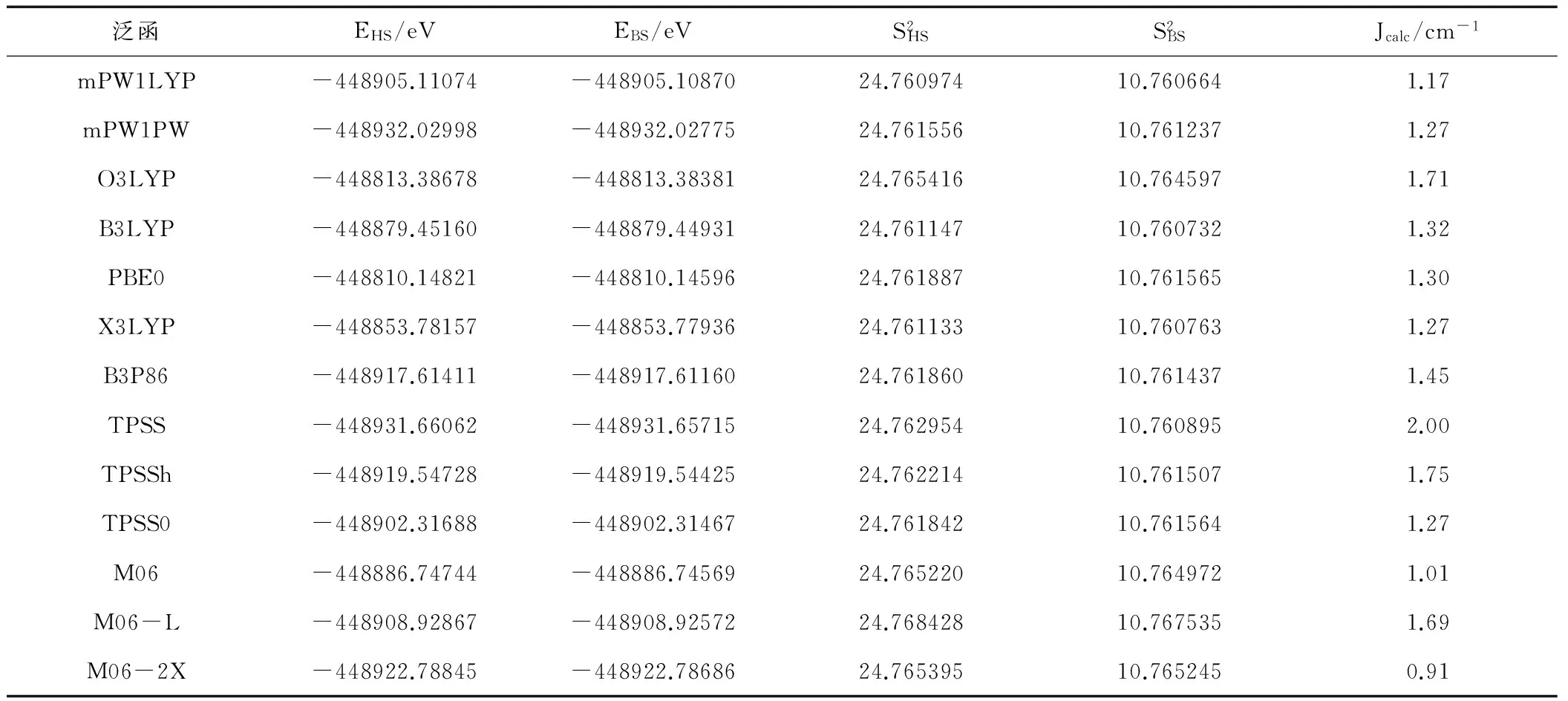
表1(续)

为了测试基组对计算结果的影响，选用PW91方法，在QZVP(SARC2-DHK-QZVP)、TZVP(SARC-DHK-TZVP)、TZVP、TZV基组下计算氧桥联希夫碱GdIIINiII双核配合物[Ni(HL)(H2O)(tfa)Gd(hfac)2]磁耦合常数Jcalc值，结果见表2。

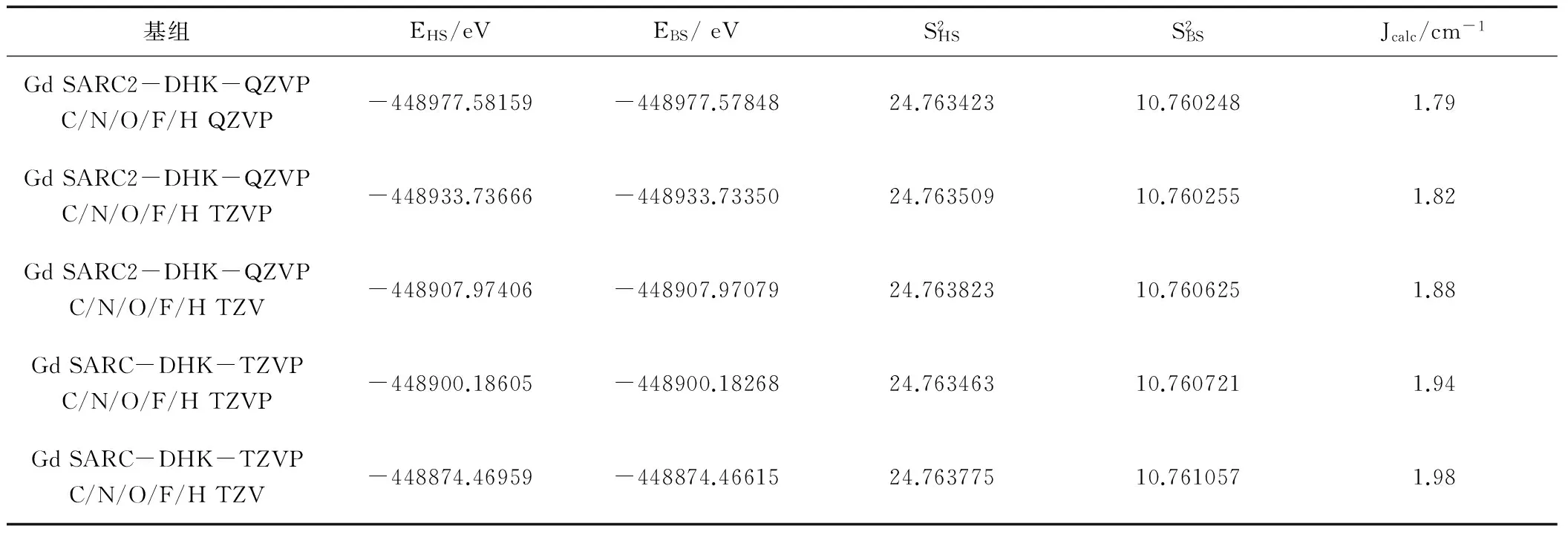
表2 PW91方法、不同基组下对磁耦合常数J的影响(Jexp=1.83 cm-1)

由表2可知，采用PW91方法在不同基组下计算氧桥联希夫碱GdIIINiII双核配合物[Ni(HL)(H2O)(tfa)Gd(hfac)2]的磁耦合常数Jcalc值，其数值1.79 cm-1至1.98 cm-1之间，其极差为0.19 cm-1，说明基组对氧桥联希夫碱GdIIINiII双核配合物磁耦合常数计算的影响不太，且选用混合基组(Gd原子为SARC2-DHK-QZVP，其他原子使用TZVP基组)计算得到的数值最吻合。所以选择在较合适的PW91/TZVP(Gd为SARC2-DHK-QZVP)水平，研究氧桥联希夫碱GdIIINiII双核配合物[Ni(HL)(H2O)(tfa)Gd(hfac)2]的磁学性质是合适的。

2.2 分子磁轨道

在分子磁学中，分析氧桥联希夫碱GdIIINiII双核配合物[Ni(HL)(H2O)(tfa)Gd(hfac)2]的分子磁轨道组成，有助于理解配合物顺磁中心间的交换作用[10，13-16]。在PW91/TZVP(Gd为SARC2-DHK-QZVP)水平计算得到氧桥联希夫碱GdIIINiII双核配合物[Ni(HL)(H2O)(tfa)Gd(hfac)2]的分子磁轨道，其中BS态下局域于某一顺磁中心的轨道为局域磁轨道，如图2(a)-(d)所示。HS态下单占据磁轨道为分子磁轨道[10，13-16]，如图3(a)-(d)所示。

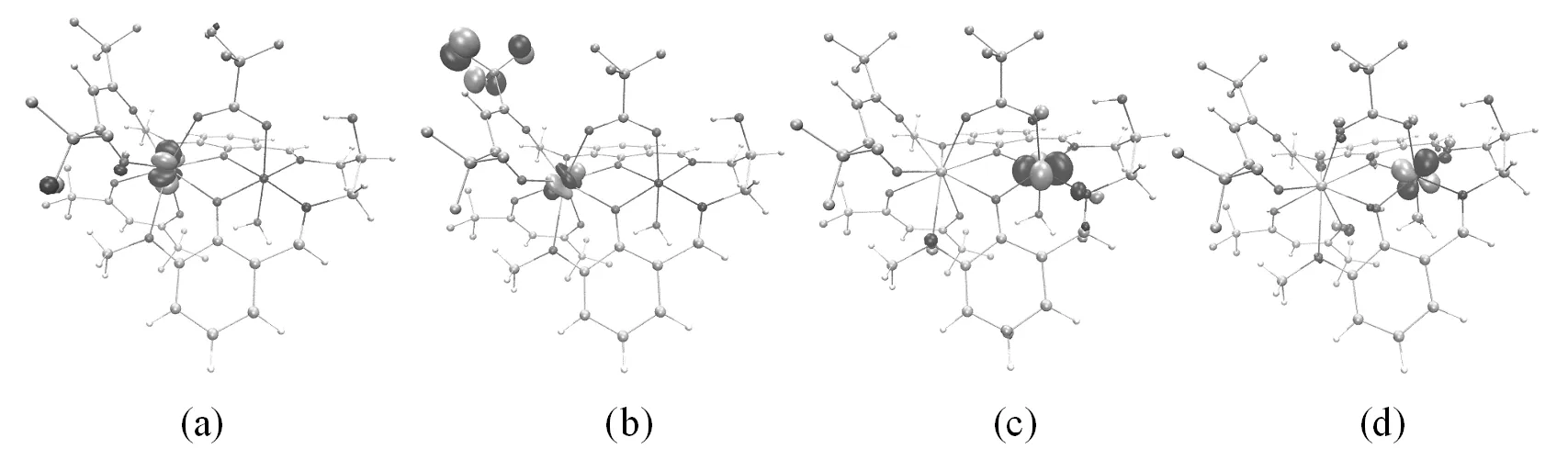
图2 GdIIINiII双核配合物[Ni(HL)(H2O)(tfa)Gd(hfac)2]局域磁轨道

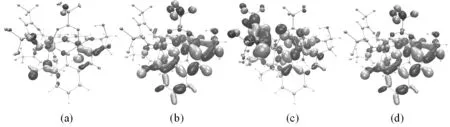
图3 GdIIINiII双核配合物[Ni(HL)(H2O)(tfa)Gd(hfac)2]分子磁轨道

由图2(a)-(d)所示的局域磁轨道可以看出，在氧桥联希夫碱GdIIINiII双核配合物[Ni(HL)(H2O)(tfa)Gd(hfac)2]中，未成对电子主要是局域在顺磁中心Gd(1)和Ni(2)，而与其配位的原子上也获得少量的电子[10]。由图3(a)-(d)所示的分子磁轨道可知，顺磁中心Gd(1)和Ni(2)与桥联配体三氟乙酸根离子、席夫碱配体之间存在较强的轨道相互作用，顺磁中心间存在三个磁交换通道，即两个氧桥(O(3)、O(4))和1个羧酸桥(O(5)、C(6)、O(7))，分子磁轨道主要由顺磁中心Gd(1)的4f轨道、顺磁中心Ni(2)的3dxz与3dx2-y2轨道、席夫碱配体提供的桥联配位O原子和三氟乙酸根离子提供的桥联配位O原子的p轨道组成。

2.3 自旋布居分析

分析氧桥联希夫碱GdIIINiII双核配合物[Ni(HL)(H2O)(tfa)Gd(hfac)2]的自旋密度分布，有利于理解顺磁中心间相互作用机理[10]。顺磁中心与周围配位原子自旋密度符号相同为自旋离域机理，相反时为自旋离域机理[10,13-17]。

在PW91/TZVP(Gd为SARC2-DHK-QZVP)水平下计算得到氧桥联希夫碱GdIIINiII双核配合物[Ni(HL)(H2O)(tfa)Gd(hfac)2]HS态和BS态的自旋密度，表3列出了BS态下顺磁中心Gd(1)、Ni(2)与周围配位原子的自旋电子在各原子轨道上的分布，其中正号和蓝色为α自旋，负号和黑色为β自旋[10]。

图4 GdIIINiII双核配合物[Ni(HL)(H2O)(tfa)Gd(hfac)2]HS和BS态的自旋密度图

从图3可知，无论HS态(图4(a))还是BS态(图4(b))，顺磁中心Ni(2)和周围配位原子O(3)、O(4)、O(7)、O(14)及席夫碱配体中N(15)、N(16)的自旋密度符号都同为负号或同为正号，即NiII离子主要是自旋离域作用[17]。无论HS态(图4(a))还是BS态(图4(b))，顺磁中心Gd(1)和周围配位原子O(3)、O(4)、O(5)、O(8)、O(9)、O(10)、O(11)、O(12)、O(13)的自旋密度符号都相反，即GdIII离子主要是自旋极化作用[17]。在BS态中，NiII离子的自旋电子(-1.566663 e)明显地离域到周围配位原子上，包括桥联配体O(3), O(4)( -0.066862 e, -0.058232 e)；端基配体N(15), N(16)( -0.086509 e, -0.089068 e)；直接与Ni配位的三氟乙酸根离子和水中的氧，即O(7)(-0.071632 e)和O(14) (-0.039298 e)。而GdIII离子的自旋电子(6.986841 e)主要是局域的，自旋密度呈球形分布，并诱导周围配位原子(三氟乙酸中的O(5)、六氟乙酰丙酮O(9)、O(10)、O(11)、O(13)和席夫碱配体中的O(3)、O (4) 、O(8)、O(12))自旋极化，其结果使得周围配位原子的自旋密度符号与GdIII离子的自旋密度符号相反[10]。从氧桥联希夫碱GdIIINiII双核配合物[Ni(HL)(H2O)(tfa)Gd(hfac)2] BS态自旋电子在各原子轨道上的分布中可以看到(如表3所示)，Ni的自旋电子主要是3d电子-1.551668 e，4s和4p上只有-0.016218 e, 0.001223 e。而Gd的自旋电子主要是4f电子6.891593 e，也有少量的5d, 6s, 6p(0.010457 e, 0.018748 e, 0.066038 e)自旋电子。其桥联配位原子O(3)、O(4)受到顺磁中心GdIII自旋极化和顺磁中心NiII自旋离域的共同作用[10，17]。其在HS态(图4 (a))和BS态(图4 (b))中都与NiII的自旋密度符号相同，说明NiII的自旋离域作用大于GdIII的自旋极化作用对桥联氧原子的影响[10，17]。

表3 GdIIINiII双核配合物[Ni(HL)(H2O)(tfa)Gd(hfac)2]BS态的自旋电子在原子轨道上的分布

3 结论

采用DFT-BS方法研究了氧桥联希夫碱GdIIINiII双核配合物[Ni(HL)(H2O)(tfa)Gd(hfac)2]，选择局域密度近似、GGA、混合泛函、meta-GGA四类方法计算了配合物的磁耦合常数，选用5种基组(QZVP(SARC2-DHK-QZVP)、TZVP(SARC-DHK-TZVP)、TZVP、TZV)进行测试。结果表明，四类方法都能用于预测氧桥联希夫碱GdIIINiII双核配合物[Ni(HL)(H2O)(tfa)Gd(hfac)2]磁学性质，但GGA泛函方法中的PW91泛函的计算值与实验值极其吻合，基组对磁耦合常数的影响不大。所以，选择在PW91/TZVP(Gd为SARC2-DHK-QZVP)水平下研究氧桥联希夫碱GdIIINiII双核配合物[Ni(HL)(H2O)(tfa)Gd(hfac)2]的磁学性质。自旋布居分析显示，Gd(1)以自旋极化为主，Ni(2)以自旋离域为主。分子磁轨道分析表明，顺磁中心间存在三个磁交换通道，即两个氧桥(O(3)、O(4)和1个羧酸桥(O(5)、C(6)、O(7))，分子磁轨道主要由顺磁中心Gd(1)的4f轨道、顺磁中心Ni(2)的3dxz与3dx2-y2轨道、席夫碱配体提供的桥联配位O原子和三氟乙酸根离子提供的桥联配位O原子的p轨道组成。

[1] Jia Y,Li J.Molecular assembly of Schiff base interactions:construction and application[J].Chem Rev，2015,115(3):1597-1621.

[2] 刘晓岚,刘永红,石尧成,等.希夫碱在有机合成中的应用研究[J].有机化学,2002,22(7):482-488.

[3] Dutt N K,Nag K.Chemistry of lanthanons-XVIII : mixed chelates of La,Pr,Nd,Sm and Y containing β-diketone and bis-salicylaldehyde ethylenediamine[J]. J.Inorg Nucl Chem,1968,30(10):2779-2783.

[4] Jiang L,Liu Y,Liu X,et al.Three series of heterometallic NiII-LNiIISchiff base complexes: synthesis,crystal structures and magnetic characterization[J].Dalton Trans,2017,46(37):12558-12573.

[5] Pasatoiu T D,Sutter J P,Madalan A M,et al.Preparation, crystal structures, and magnetic features for a series of dinuclear [Ni(II)Ln(III)] Schiff-base complexes:evidence for slow relaxation of the magnetization for the Dy(III) derivative.[J].Inorg Chem,2011,50(13):5890-5898.

[6] Xie Q W,Wu S Q,Liu C M,et al.Synthesis,crystal structure and magnetic properties of dinuclear NiIILNiIIcomplexes based on a flexible polydentate ligand[J].Dalton Trans,2013,42(31):11227-11233.

[7] Pasatoiu T D,Etienne M,Madalan A M,et al.Crystal structures and magnetic properties of two new heterodinuclear [NiIILNiII] complexes obtained using a side-off compartmental ligand and 2,6-pirydin-dicarboxylato coligand[J]. Revue Roumaine De Chimie,2012,57(4):507-512.

[8] Colacio E,Ruiz J,Mota A J,et al.Family of carboxylate- and nitrate-diphenoxo triply bridged dinuclearNiIILNiIIcomplexes(Ln=Eu,Gd,Tb,Ho,Er,Y):synthesis, experimental and theoretical magneto-structural studies,and single-molecule magnet behavior[J].Inorg Chem,2012,51(10):5857-5868.

[9] Ahmed N,Das C,Vaidya S,et al.Nickel(II)-lanthanide(III) magnetic exchange coupling influencing single-molecule magnetic features in {Ni2Ln2} complexes[J].Chem Eur J,2014,20(44):14235-14239.

[10] 罗树常,范光鼎,郑鹏飞,等.氧桥联GdNi双核配合物磁性与结构关系理论研究[J].分子科学学报,已录用.

[11] Neese F.The ORCA Program System[J].WIREs Comput Mol Sci,2012,2(1):73-78.

[12] Humphrey W,Dalke A,Schulten K.VMD:Visual Molecular Dynamics[J].J Mol Graphics,1996,14(1):33-38.

[13] 曹景阳,孙小媛,罗树常,等.氧桥联席夫碱GdCo双核配合物磁学性质理论研究[J].广东化工,2017,44(7):130-132.

[14] 罗树常,刘翔宇,张竹霞,等.氧桥联稀土钆双核配合物磁学性质的密度泛函理论研究[J].分子科学学报,2017,33(2):120-126.

[15] 胡宗超,卫海燕,王 凡,等.密度泛函理论在分子磁学中的应用2.混合桥联三核镍配合物自旋交换作用[J].化学学报,2004,62(20):1973-1980.

[16] Bian J Y,Chang Y F,Zhang J P.Theoretical studies on the magnetic bistability of dinickel complex tuned by azide[J].J Phys Chem A,2008,112:3186-3191.

[17] 阎 峰,陈志达.密度泛函理论方法研究稀土-过渡金属化合物的磁性和自旋密度图[J].北京大学学报(自然科学版),2000,36(6):873-880.