预制综合管廊橡胶密封垫受压性能研究及断面设计

张铨婧， 莫海鸿， 黄臣瑞， 陈俊生, *

(1. 华南理工大学土木与交通学院， 广东 广州 510640；2. 华南理工大学亚热带建筑科学国家重点实验室， 广东 广州 510640)

0 引言

预制综合管廊拼缝接头处常常采用预制的弹性密封垫作为主要防水措施[1]。拼缝弹性密封垫应沿环、纵面成框。将弹性密封垫置于沟槽中，沟槽形式、尺寸应与弹性密封垫相匹配。拼缝接头防水构造示意图如图1所示。目前密封垫主要采用氯丁橡胶和三元乙丙橡胶等材料[2]，也可选用弹性橡胶与遇水膨胀橡胶制成的复合密封垫。复合密封垫宜采用中间开孔、下部开槽的断面构造形式。

橡胶密封垫压密(压缩度达到50%)时所需的装配力既需要满足防水要求(在综合管廊接缝宽度为5 mm时，橡胶密封垫界面应力不小于1.5 MPa)，也需要满足装配能力。除橡胶密封垫的材料之外，不同的断面形式也会对橡胶密封垫压密时需要的装配力造成影响。目前已有的相关研究均是针对盾构隧道的橡胶密封垫进行的，例如： 欧阳文彪[3]研究了橡胶硬度和开孔大小对盾构隧道橡胶密封垫力学性能的影响； 向科等[4]和雷震宇[5]对盾构隧道橡胶密封垫的断面形式进行了调整和优化； 谭文怡[6]对橡胶密封垫受到高温后的压缩性能进行了研究。其他研究或是在橡胶密封垫的耐久性和寿命预测方面[7-8]，或是在防水性能和防水技术方面[9-12]。

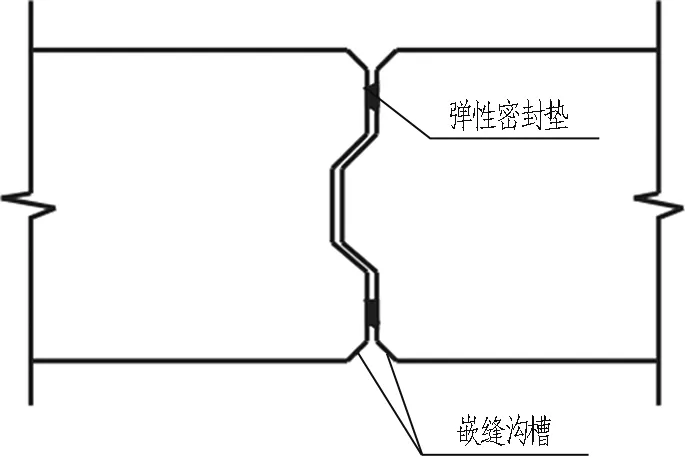
图1 拼缝接头防水构造示意图

综合来看，在受压性能方面，已有的研究对断面形式考虑得并不全面，断面形式包括了开槽形式和开孔形式。另外，与盾构隧道不同的是： 预制综合管廊采用吊车进行装配，由张拉机提供装配力，张拉机难以提供盾构所能提供的装配力。因此，需采用模量更小的橡胶密封垫。由于综合管廊的接头形式与盾构隧道不同，因而橡胶密封垫的尺寸和形状也不同。因此，对于综合管廊，不能完全按照盾构隧道进行橡胶密封垫的断面设计，需要进行有针对性的研究。通过大量的对比试验对断面形式进行调整虽然可行，但生产橡胶密封垫以及试验周期较长，且成本难以控制，因此，有必要采取数值模拟的方式对其进行研究。

本文针对某城市预制综合管廊的橡胶密封垫断面设计，进行了橡胶密封垫压缩试验，并利用通用有限元软件MSC.Marc对橡胶密封垫的压缩过程进行了模拟； 然后，将模拟结果与试验结果进行对比，验证了有限元模拟结果的可靠性； 最后，探讨了不同开槽和开孔形式对橡胶密封垫受压性能的影响。

1 橡胶密封垫压缩试验

本次压缩试验取3个相同的试样，试样为遇水膨胀橡胶和三元乙丙橡胶组成的复合橡胶密封垫。对试样只开槽，不开孔，试样长度为20 mm，长度公差为-1 mm。橡胶密封垫断面形状和尺寸如图2所示。

利用预先制备的带有沟槽的钢模具模拟橡胶密封垫实际装配时的管廊接头沟槽。沟槽示意图如图3所示。采用新三思电子式万能材料试验机进行加载试验，测定橡胶密封垫压缩度为50%时的最大压力，其中，该橡胶密封垫压缩度为50%时竖向压缩位移需达到10 mm。加载试验装置如图4所示。

图2 橡胶密封垫断面形状和尺寸(单位： mm)

Fig. 2 Shape of cross-section of rubber gasket and its size (unit： mm)

图3 沟槽示意图(单位： mm)

图4 加载试验装置

试验开展前，应将试样在标准温度(23±2) ℃下放置16 h。试验在标准温度(23±2) ℃下进行。试验时先将试样放置在试验装置的模具沟槽里，试验机以50 mm/min的速率加载，直至压缩量为10 mm，再以相同速率卸载至压力为0 N，如此反复加载和卸载3次。根据试验结果绘出荷载-位移曲线，并根据第3次压缩试验确定压缩位移为10 mm时的压力值。

由试验结果得出，复合橡胶密封垫试样压缩位移为10 mm时，压力平均值为541.7 N。以此换算出复合橡胶密封垫每延米的装配力约为27.085 kN，实际施工时难以达到。因此，需对橡胶密封垫进行开孔设计。

2 橡胶密封垫有限元模型

橡胶压缩模型存在着复杂的接触问题以及非线性和大变形问题。MSC.Marc是功能齐全的高级非线性有限元软件，具有极强的结构分析能力，支持全自动二维网格和三维网格重划分，同时，可用以纠正过渡变形后产生的网格畸变，确保大变形分析的继续进行。因此，利用MSC.Marc模拟橡胶压缩过程具有很强的操作性。

橡胶材料的本构模型采用工程中应用广泛的Mooney-Rivlin模型[13-14]，假定橡胶材料在短时间内以及恒温下为各向同性的不可压缩材料，橡胶应变能密度函数W是变形张量不变量的函数，表达式为

W=C10(I1-3)+C01(I2-3)。

(1)

式中：I1和I2是应变张量不变量；C10和C01是本构模型的参数。

根据文献[15]，通过测量三元乙丙橡胶的硬度(IRHD硬度)，并取C01/C10=0.05，求得本构模型的参数C10=0.23，C01=0.01。由于试验中采用的遇水膨胀橡胶与三元乙丙橡胶的硬度相同，因此，遇水膨胀橡胶材料采用与三元乙丙橡胶相同的参数。

为了提高计算效率，可将橡胶压缩问题简化为平面应变问题。在本模型中，将橡胶设置为变形体，由于压板和垫板的刚度比橡胶大得多，可以不考虑压板和垫板的变形，因此，将压板和垫板设置为刚体。橡胶的计算单元采用4节点四边形的Herrmann单元，Herrmann单元可模拟橡胶的体积不可压缩特性。由于遇水膨胀橡胶和三元乙丙橡胶粘结紧密，故不考虑它们之间的相互错动，认为它们节点耦合。建模时对于橡胶与压板、垫板之间的接触，摩擦因数取0.3，对于橡胶自接触，摩擦因数取0.6[16]，并设置网格在畸变时自动重划分。为了使模型收敛，对垫板直角处进行了倒圆角处理。橡胶密封垫模型示意图如图5所示。与橡胶压缩试验相同，使压板向下运动，挤压橡胶，直至橡胶压缩量达到10 mm。

图5 橡胶密封垫模型示意图

压缩位移为10 mm时，橡胶密封垫接触应力云图如图6所示。由图6可知，压缩位移为10 mm时，最大接触应力为5.014 MPa，接触应力最大位置在橡胶与垫板阳角接触部位。

橡胶压缩时所需压力等于所有与压板接触的节点竖向力之和。由此计算所得的压缩应力-应变曲线与试验结果得到的压缩应力-应变曲线如图7所示。

图6压缩位移为10 mm时橡胶密封垫接触应力云图(单位： MPa)

Fig.6 Contact stress nephogram of rubber gasket when compression displacement is 10 mm (unit： MPa)

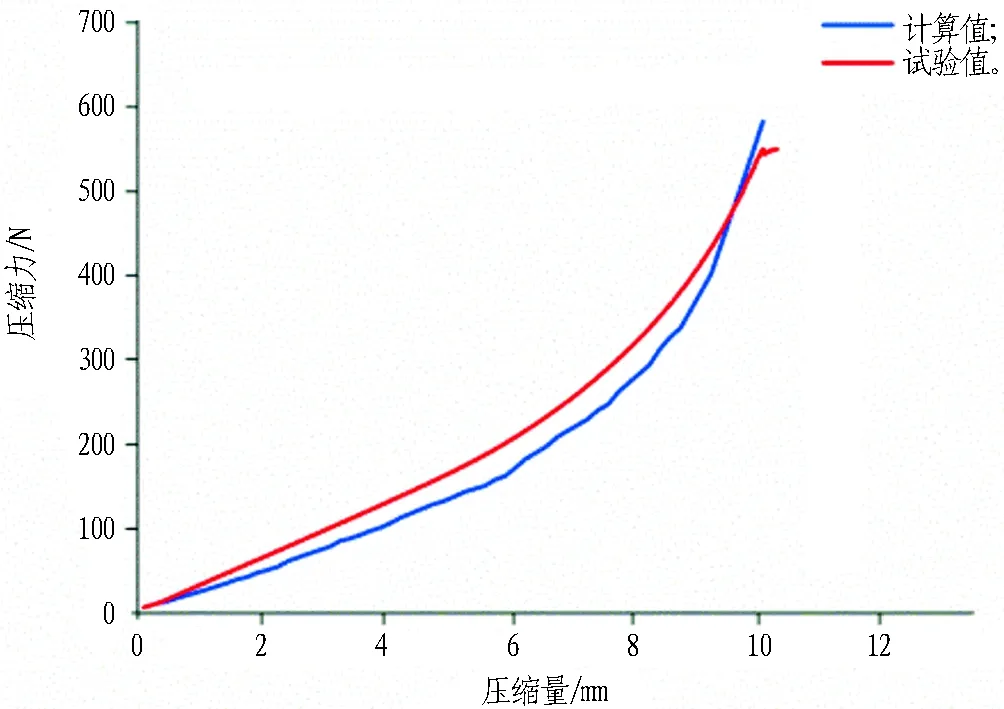
图7 压缩应力-应变曲线

由图7可以看出，计算所得的压缩应力-应变曲线与试验结果得到的压缩应力-应变曲线基本吻合。说明计算所采用的本构模型以及参数是合理的，有限元方法能够较为准确地模拟橡胶密封垫的压缩过程。橡胶密封垫的压缩分为2个阶段： 第1阶段以内部孔洞的压缩为主； 第2阶段随着内部孔洞的压密，所需压缩力增大[17]。因此，压缩应力-应变曲线先是呈线性增长，在压缩量达到5 mm左右后，曲线的斜率逐渐增大。通过数值模拟计算得到压缩位移为10 mm时橡胶密封垫每延米装配力为28.8 kN，与试验值相差1.715 kN。

3 开槽设计

在研究开孔对橡胶密封垫受压性能的影响之前，先研究开槽的影响。橡胶密封垫的开槽形式可以是试验中的半圆加正方形槽，也可以是半圆槽、半圆加梯形槽； 可以设计成2槽，也可以设计成3槽。不同槽数量及形状的橡胶密封垫模型如图8所示。研究从以下2个方面入手： 一是研究开槽大小对装配力和接触应力的影响； 二是研究开槽数量和形状对装配力和接触应力的影响。

(a) 2槽(半圆加正方形槽) (b) 2槽(半圆槽)

(c) 2槽(半圆加梯形槽) (d) 3槽(半圆加正方形槽)

Fig. 8 Rubber gasket models with different grooving number and shapes

3.1 开槽大小的影响

采用如图8所示的2个半圆加正方形槽，半圆形的直径和正方形的边长相等，即半圆形的直径等于槽的宽度。通过改变槽的宽度以改变开槽大小，研究开槽大小对接触应力以及装配力(由压缩力换算得到)的影响。取不开槽和开槽2种情况，不开槽时槽的宽度记为0 mm，开槽时槽的宽度取 2～4 mm，槽的宽度为4 mm时与压缩试验相对应。压缩位移为10 mm时不同槽宽度情况下橡胶密封垫的装配力和最大接触应力如图9所示。

(a) 装配力

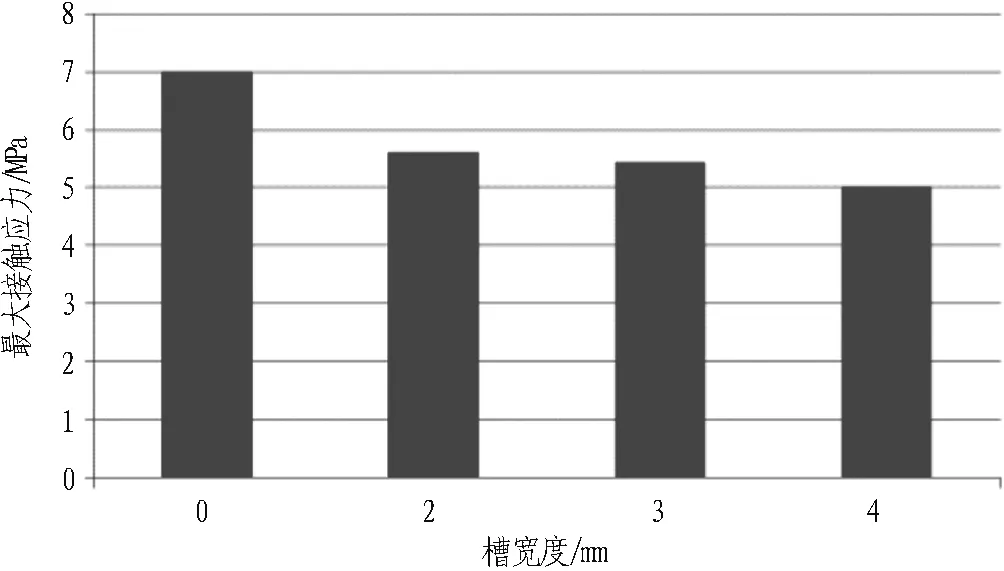
(b) 最大接触应力

图9压缩位移为10 mm时不同槽宽度情况下橡胶密封垫的装配力和最大接触应力

Fig. 9 Compressive force and maximum contact stress of rubber gaskets with different grooving widths when compression displacement is 10 mm

由图9可以看出，开槽后，橡胶密封垫压缩位移为10 mm时接触应力和装配力均比不开槽时小。槽宽度不同情况下接触应力最大位置在橡胶与垫板阳角接触部位。随着槽宽度的增大，橡胶密封垫的接触应力减小，装配力也减小。不开槽时最大接触应力为7.012 MPa，每延米所需装配力约为 43.92 kN，比试验中采用的橡胶密封垫施工时装配更加困难。

3.2 开槽数量及开槽形状的影响

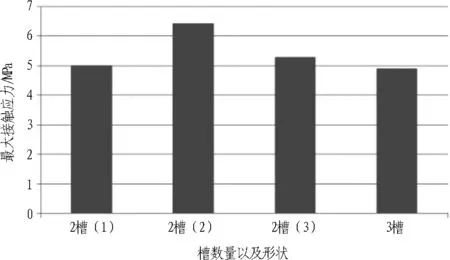
通过控制槽的总面积不变，改变槽的数量及形状，研究槽的数量和形状对接触应力以及装配力的影响。取2个直径为4 mm半圆加正方形槽的面积作为标准，记为2槽(1)。当橡胶密封垫上有3个半圆加正方形槽时，每个半圆槽孔直径为3.266 mm，正方形边长为 3.266 mm，记为3槽； 当有2个半圆槽时，每个槽的直径为7.534 mm，记为2槽(2)； 当橡胶密封垫上的槽孔形状为2个半圆加梯形槽时，半圆槽孔直径为3.824 mm，梯形上底宽3.824 mm，下底宽4.824 mm，高为3.824 mm，记为2槽(3)。压缩位移为10 mm时不同槽数量及形状的橡胶密封垫的装配力和最大接触应力如图10所示。

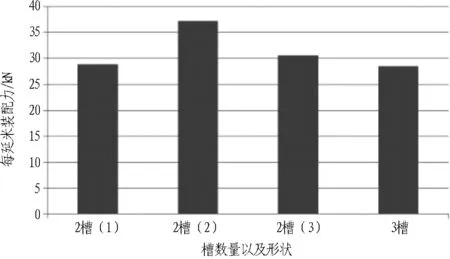
(a) 装配力

(b) 最大接触应力

图10压缩位移为10 mm时不同槽数量及形状的橡胶密封垫的装配力和最大接触应力

Fig. 10 Compressive force and maximum contact stress of rubber gaskets with different grooving number and shapes when compression displacement is 10 mm

由图10可以看出，开槽面积相同时，槽的数量对接触应力和装配力影响较小，采用2槽或3槽时橡胶密封垫的接触应力和装配力相差很小； 槽的形状对接触应力和装配力的影响较大，采用半圆形槽时接触应力和装配力最大，采用半圆加正方形槽时接触应力和装配力最小。图10(b)中2槽(1)、2槽(3)以及3槽的接触应力最大位置在橡胶与垫板阳角接触部位，而2槽(2)接触应力最大位置在槽孔自接触处。因此，建议选用2个或3个半圆加正方形槽形式。

4 开孔设计

橡胶密封垫的孔可设计成2孔、平排3孔、错排3孔、直排4孔、斜排4孔以及5孔，如图11所示。研究从以下2方面入手： 一是研究开孔大小对装配力和接触应力的影响； 二是研究开孔数量和排列方式对装配力和接触应力的影响。

(a) 2孔 (b) 3孔(平排)

(c) 3孔(错排) (d) 4孔(直排)

(e) 4孔(斜排) (f) 5孔

图11不同孔数量及排列位置的橡胶密封垫模型

Fig. 11 Rubber gasket models with different opening number and arrangement modes

4.1 开孔大小的影响

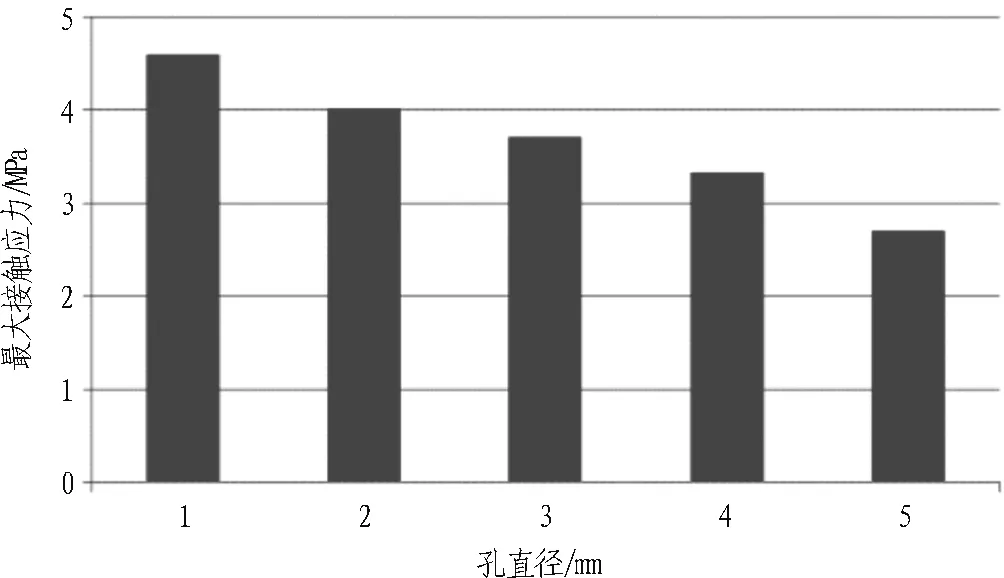
以图11所示的2孔为例，控制孔的数量和位置不变，通过改变孔直径以改变开孔大小，研究开孔大小对接触应力以及装配力的影响，孔的直径取1～5 mm。压缩位移为10 mm时不同孔直径情况下橡胶密封垫的装配力和最大接触应力如图12所示。

由图12可以看出，开孔后，压缩位移为10 mm时橡胶密封垫的接触应力和装配力均比不开孔时小。孔直径为1～2 mm时接触应力最大位置在橡胶与垫板阳角接触部位，孔直径为3～5 mm时接触应力最大位置在橡胶底部的中间部位。随着孔直径的增大，橡胶密封垫的接触应力和装配力均减小。当开孔直径达到5 mm时，最大接触应力为2.689 MPa，每延米所需装配力约为16.92 kN，比试验中采用的橡胶密封垫施工装配要容易得多。

(a) 装配力

(b) 最大接触应力

图12压缩位移为10 mm时不同孔直径情况下橡胶密封垫的装配力和最大接触应力

Fig. 12 Compressive force and the maximum contact stress of rubber gaskets with different opening diameters when compression displacement is 10 mm

4.2 开孔数量及排列位置的影响

通过控制开孔面积不变，改变开孔数量及排列方式，研究开孔数量及排列方式对接触应力以及装配力的影响。以2个直径为5 mm圆孔的面积作为标准(记为2孔)，换算成3孔时孔的直径为4.082 mm，平排记为3孔(1)，错排记为3孔(2)； 换算成4孔时孔的直径为3.536 mm，直排记为4孔(1)，斜排记为4孔(2)； 换算成5孔时孔的直径为3.162 mm，记为5孔。开孔数量及排列位置不同情况下压缩位移为10 mm时橡胶密封垫的装配力和最大接触应力如图13所示。

由图13可以看出，橡胶密封垫开孔面积相同时，开孔数量及排列方式对接触应力和装配力的影响不大，接触应力最大位置均在橡胶底部的中间部位。通过对开孔数量为3孔的2种布置进行比较可知，错排时比平排时接触应力和装配力小。通过对开孔数量为4孔的2种布置比较可知，斜排时比直排时接触应力和装配力小。由于开孔数量越多，制造难度越大，因此，建议选用2孔或者3孔错排布置方式。

(a) 装配力

(b) 最大接触应力

图13开孔数量及排列位置不同情况下压缩位移为10 mm时橡胶密封垫的装配力和最大接触应力

Fig. 13 Compressive force and maximum contact stress for rubber gaskets with different opening number and arrangement modes when compression displacement is 10 mm

5 结论与建议

针对不同的橡胶密封垫断面形式，通过压缩试验以及数值模拟，得到以下主要结论：

1)有限元方法能够较为准确地模拟橡胶密封垫的压缩过程，并能准确分析其受压性能，说明利用有限元软件对橡胶密封垫进行断面设计和优化是可行的。

2)在同一种尺寸和硬度下，压缩度为50%时随着开槽和开孔面积的增大，橡胶密封垫的接触应力和装配力减小。开槽面积相同时，2槽和3槽橡胶密封垫的接触应力和装配力相差很小，槽形状为半圆加正方形时接触应力和装配力最小，因此，建议选用2个或者3个半圆加正方形槽形式的橡胶密封垫。开孔面积相同时，不同开孔数量以及排列方式橡胶密封垫的接触应力和装配力相差不大，但仍有影响，建议选用2孔或者3孔错排的开孔形式。

本文只研究了在同一种尺寸和硬度下，开槽和开孔形式对橡胶密封垫接触应力和装配力的影响，对于橡胶密封垫尺寸、外轮廓形状、遇水膨胀橡胶和三元乙丙橡胶的硬度组合等因素的影响以及橡胶密封垫的耐久性和防水性能等方面均未进行研究，因此，建议开展进一步的研究。

参考文献(References):

[1] 城市综合管廊工程技术规范： GB 50838—2015[S]. 北京: 中国计划出版社, 2015.

Technical code for urban utility tunnel engineering: GB 50838-2015[S]. Beijing: China Planning Press, 2015.

[2] 王民. 隧道盾构施工管片橡胶密封垫的材料和结构及产品性能特性[J]. 特种橡胶制品, 2005, 26(1): 42.

WANG Min. Material and structure of rubber gasket for shield driven tunnel segment and characteristic of the products[J]. Special Purpose Rubber Products, 2005, 26(1): 42.

[3] 欧阳文彪. 盾构隧道橡胶密封垫力学性能试验及数值分析[J]. 隧道建设, 2013, 33(11): 933.

OUYANG Wenbiao. Mechanical test and numerical analysis of elastic gaskets of shield tunnels[J]. Tunnel Construction, 2013, 33(11): 933.

[4] 向科, 石修巍. 盾构管片弹性密封垫断面设计与优化[J]. 地下空间与工程学报, 2008(2): 361.

XIANG Ke, SHI Xiuwei. Design and optimization of elastic gasket section of shield tunnel lining[J]. Chinese Journal of Underground Space and Engineering, 2008(2): 361.

[5] 雷震宇. 盾构隧道管片橡胶密封垫的优化设计方法[J]. 地下空间与工程学报, 2010(4): 770.

LEI Zhenyu. An optimal design approach for the rubber sealing gasket in shield tunneling[J]. Chinese Journal of Underground Space and Engineering, 2010(4): 770.

[6] 谭文怡. 盾构隧道管片接头密封垫的高温后性能研究[D]. 广州： 华南理工大学, 2015.

TAN Wenyi. Research on property of rubber gaskets in shield tunneling joints after high temperature[D]. Guangzhou: South China University of Technology, 2015.

[7] 莫一婷, 杨林德, 伍振志, 等. 遇水膨胀橡胶的老化性能试验研究及寿命预测[J]. 地下空间与工程学报, 2009(2): 235.

MO Yiting, YANG Linde, WU Zhenzhi, et al. Experimental research on aging performance and service life forecast of water-swelling rubber[J]. Chinese Journal of Underground Space and Engineering, 2009(2): 235.

[8] 丁杨, 孟伟, 邓文武. 盾构管片橡胶密封垫断面形式设计及耐久性研究[J]. 华东交通大学学报, 2016, 33(4): 45.

DING Yang, MENG Wei, DENG Wenwu. Study of durability and section design of sealing rubber pad of shield segment[J]. Journal of East China Jiaotong University, 2016, 33(4): 45.

[9] 樊庆功, 方卫民, 苏许斌. 盾构隧道遇水膨胀橡胶密封垫止水性能试验研究[J]. 地下空间, 2002, 22(4): 335.

FAN Qinggong, FANG Weimin, SU Xubin. Experimental study of the waterproof capability of the hydro-expansive rubber sealing cushion in shield tunnel[J]. Underground Space, 2002, 22(4): 335.

[10] 胡翔, 薛伟辰, 王恒栋. 上海世博园区预制预应力综合管廊接头防水性能试验研究[J]. 特种结构, 2009, 26(1): 109.

HU Xiang, XUE Weichen, WANG Hengdong. Experimental studies of mechanical properties of PPMT in Shanghai Expo Area[J]. Special Structures, 2009, 26(1): 109.

[11]GONG Chenjie, DING Wenqi, JIN Yuelang, et al. Waterproofing performance of shield-driven tunnel's segment joint under ultra high water pressure[C]//American Society of Civil Engineers. Shanghai: [s.n.], 2014.

[12] 朱祖熹. 盾构隧道管片接缝密封垫防水技术的现状与今后的课题[J]. 隧道建设, 2016, 36 (10): 1171.

ZHU Zuxi. State-of-art and developing direction of waterproofing technology for sealing gasket of shield tunnel segment joints[J]. Tunnel Construction, 2016, 36 (10): 1171

[13] 秦正贵. 盾构隧道EPDM橡胶密封垫本构参数试验研究[J]. 隧道建设, 2017, 37(7): 816.

QIN Zhenggui. Experimental study of constitutive parameters of ethylene-propylene-diene monomer(EPDM) rubber gasket used in shield tunnel[J]. Tunnel Construction, 2017, 37(7): 816.

[14] ARRUDAE M, BOYCEM C. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials [J]. Transactions of the Faraday Society, 1993, 42(2): 389.

[15] 郑明军, 王文静, 陈政南, 等. 橡胶Mooney-Rivlin模型力学性能常数的确定[J]. 橡胶工业, 2003, 50(8): 462.

ZHENG Mingjun, WANG Wenjing, CHEN Zhengnan, et al. Determination for mechanical constants of rubber Mooney-Rivlin model[J]. China Rubber Industry, 2003, 50(8): 462.

[16] 周书扬. 钢板加固地铁盾构隧道纵缝接头承载性能的数值研究[D]. 广州： 华南理工大学, 2015.

ZHOU Shuyang. Numerical study of bearing behavior of longitudinal joint reinforced by steel plate in metro shield tunnel[D]. Guangzhou: South China University of Technology, 2015.

[17] 陈俊生, 莫海鸿. 盾构隧道管片接头抗弯刚度的三维数值计算[J]. 铁道学报, 2009, 31(4): 87.

CHEN Junsheng, MO Haihong. Three-dimensional FEM analysis on flexural rigidity of segment joints in shield tunnel[J]. Journal of the China Railway Society, 2009, 31(4): 87.