泥水盾构水平直管内石碴起动速度研究

夏毅敏， 姚 菁， 吴 遁， 陈 鹏， 王 洋

(1. 中南大学高性能复杂制造国家重点实验室， 湖南 长沙 410083；2. 中铁十四局集团隧道工程有限公司， 山东 济南 250013；3. 中铁十四局集团大盾构工程有限公司， 南京 江苏 210000)

0 引言

随着我国城市地下空间和跨江越海隧道工程数量的不断增长，泥水盾构施工技术得到越来越广泛地应用[1-2]。泥水环流系统作为泥水盾构输送石碴的核心系统，在卵砾石地层掘进时极易发生石碴堆积、采石箱堵塞和排浆泵供能不足等一系列问题。颗粒由静止变为运动的临界状态称为颗粒起动[3-4]，研究石碴在管道内的起动特性有利于减小环流系统输送能量损耗，减少石碴大量堆积现象发生。

目前国内外学者针对颗粒运动特性开展了一系列相关研究。在实验研究方面，刘明潇等[5]通过实验分析粗细颗粒间相互作用，研究颗粒粗细比、粒径级差和当量粒径等非均匀因子对颗粒推移运动的影响；王继红等[6]研究了在不同输送速度、不同冰粒子浓度及不同管径下冰浆流体所表现出的非牛顿流变特性和阻力特性；曹斌等[7]通过高速摄影技术和粒子图像测速分析不同粒径、体积分数和输送速度条件下粗颗粒在管道中的水力学特性；Jin等[8]通过目视观察和粒子示踪技术研究颗粒形状对流型、放电率、平均粒子停留时间和示踪剂浓度的影响；周知进等[9]实验研究颗粒组分特性与输送速度之间的关系。在计算机模拟方面，Zhao等[10]运用球状团块建立非球形粒子模型，研究三维可压缩条件下颗粒的剪切行为；Akhshik等[11]通过计算流体力学与离散单元法相结合，研究颗粒形状对钻井输送特性的影响；张芝永等[12]建立了海底管线周围水动力场-渗流场耦合数值模型，分析波浪KC数、相对埋深e/D对管线两端压差的影响；陶贺等[13]采用多元颗粒模型分析运动过程中的受力特性，研究颗粒物性对流型、空隙率分布以及颗粒分离情况的影响；宋晓阳等[14]利用直接数值模拟、点球浸入边界法和颗粒离散元法相结合的方法，定量研究颗粒在湍流边界层中的运动和分布规律；Jiang等[15]通过考虑颗粒-粒子和粒子-壁相互作用，采用二维欧拉-欧拉多相流模型研究流速和固体体积分数对氮浆的流动特性的影响。

上述学者研究的颗粒粒径绝大部分低于20 mm，仿真采用的也是球形颗粒模型，目前还没有关于泥水盾构环流管道中大粒径非球形石碴输送方面的研究成果。本文针对泥水盾构环流系统中大粒径(最大轴线距离为30～90 mm)非球形石碴，以排浆管入口段水平直管为研究对象，采用计算流体力学软件结合离散单元法研究石碴形状系数、等容粒径和数量对石碴起动速度的影响。

1 石碴形貌和浆液特性

1.1 石碴形貌特征

兰州某穿黄工程施工始发段地层中富含砂卵石，从泥水分离站提取3种典型石碴形貌，如图1所示。从图中可以看出石碴外形有扁平状、椭球体及近球形3种形状，为方便论述，石碴形貌以石碴形状系数来表征，见式(1)，其三轴尺寸如表1所示。石碴体积以等容粒径，即真实体积与颗粒相等的球体直径来表征，见式(2)。本文主要针对非球形石碴，研究石碴形状系数对起动速度的影响，其石碴仿真模型如图2所示。从图1和图2对比可得，所建立的石碴模型比较接近真实的石碴形状。

(a) 扁平状(b) 椭球体 (c) 近球形

图1不同形状石碴

Fig. 1 Pebbles with different shapes

(1)

Dv=(6VS/π)1/3。

(2)

式中：Sf为石碴形状系数；a、b、c为石碴的3个轴线尺寸长度，a为最长轴线距离，c为最短轴线距离；Dv为石碴等容粒径；VS为石碴真实体积。

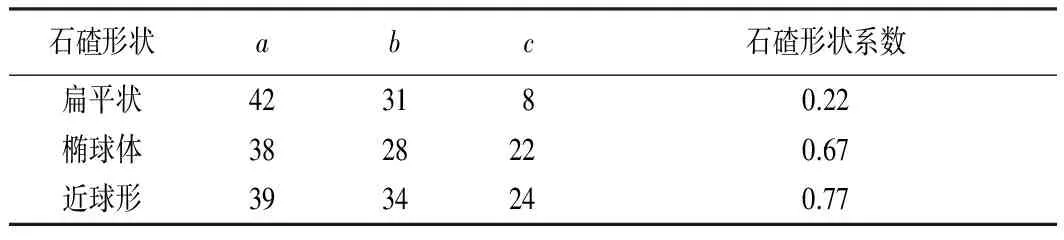
表1 石碴三轴尺寸表

(a)Sf=0.2(扁平状) (b)Sf=0.65(椭球体) (c)Sf=0.80(近球形)

图2不同形状系数石碴仿真模型

Fig. 2 Simulation models of pebbles with different shapes

1.2 浆液流变特性

兰州某穿黄工程泥水盾构所使用泥浆主要由水、膨润土、红土和制浆剂通过一定比例配置而成。提取施工现场泥浆试样，通过六速旋转流变仪进行流变实验，测得剪切速率和剪切应力呈线性关系(其判定系数R2=0.993)，满足宾汉流体流变方程，见式(3)，其流变模型为τ=3.98+0.009 12γ，流变曲线如图3所示。

τ=τd+μpγ。

(3)

式中：τ为剪切应力；τd为屈服应力；μp为塑性黏度；γ为剪切速率。

图3 泥浆流变曲线

2 数学模型

2.1 流体相

泥浆流动过程遵循质量守恒定律和动量守恒定律，因不考虑泥浆和石碴之间的热传递与相变，故不考虑能量守恒方程。

连续性方程：

(4)

动量方程：

(5)

式中：ρ为液体密度；t为时间；u为液体流速；ρf为颗粒体积力；p为压力梯度力；τ为浆液黏性力。

泥浆在输送管道内的流动为湍流运动，Standardk-w模型尤其适合绕流运动计算，其控制方程为：

(6)

(7)

式中：Γk和Γw表示k和w的扩散率；Gk是由速度梯度产生的湍流动能，Gw由方程w产生；Yk和Yw是由扩散产生的湍流。

2.2 颗粒相

石碴在管道输送过程中受到其他石碴、管壁和泥浆的作用力，其运动模型如下：

(8)

式中：mi、Up,i分别为石碴i的质量、速度；Fc,ij为石碴i与石碴j之间的接触力；Fd,i为石碴i受到管壁的摩擦力；Ff,i为石碴i与泥浆之间的作用力。

石碴和泥浆之间的作用力主要由浮力FB、拖曳力FD和压力梯度力Fp组成，其计算公式分别如下：

(9)

(10)

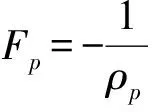
(11)

式中：ρp为石碴密度；Up为石碴速度；dp为石碴直径；μe为泥浆有效黏度。颗粒雷诺数Rep和阻力系数CD计算公式分别如下：

(12)

(13)

式中：Uf为泥浆速度；Re为流体雷诺数；a1、a2、a3为雷诺数常量。

2.3 几何模型和边界条件设置

水平管道长5 m，直径为300 mm，几何模型如图4所示。为研究石碴的起动速度，即石碴从静止状态变为运动状态的那一时刻的速度，在管道内放置石碴，石碴密度为2 700 kg/m3，泥浆密度为1 200 kg/m3，并设置匀加速的浆液入口流速，其自定义函数(UDF)为：vm=2tm/s。由此可得出不同参数变化下石碴的起动时间ts(对应速度曲线上的拐点)，则石碴起动速度vi=2tsm/s，如图5所示。湍流模型选用Standardk-w流场模型，关闭能量方程；边界条件采用速度进口边界条件，总压出口边界条件，壁面无滑移边界条件；并采用Phase Coupled SIMPLE算法求解速度、压力耦合方程。

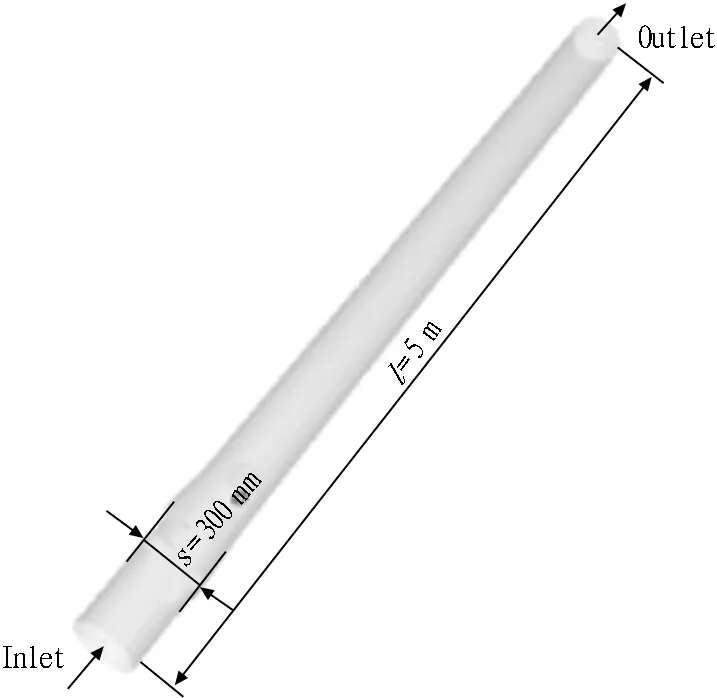
图4 几何模型

图5 石碴运动速度

3 石碴起动速度影响因素研究

3.1 形状系数对石碴起动速度的影响

为研究形状系数对石碴颗粒起动速度的影响，在离入口面一定距离处管道底部放置单个石碴，石碴等容粒径Dv=38.5 mm。不同形状系数下的石碴起动速度如图6所示。由图6可知： 当石碴形状系数Sf在0.20～0.37和0.80～0.952时，石碴起动速度随形状系数的增大呈下降趋势，石碴起动速度最大值分别为0.589 m/s和0.2 m/s；当石碴形状系数Sf=0.55时，与形状系数Sf=0.37相比，石碴起动速度发生跃变，石碴起动速度达到1.4 m/s，增幅达到204%。椭球状石碴角速度(Sf=0.72)如图7所示。从图7可以看出： 石碴x、y方向的角速度较大，且x方向明显大于y方向，x方向角速度最大值为0.75 rad/s，而y方向角速度仅为0.11 rad/s，z方向角速度几乎为0；x、y方向角速度在0点上下振动，且随着时间的增大振动幅值逐渐变小，最终趋于0，此时刻为0.69 s，是石碴的起动时刻点。由此可得在0.69 s之前，椭球状石碴绕x和y方向做旋转运动，且绕x方向运动较为剧烈，在0.69 s之后开始起动。

图6 不同形状系数下石碴起动速度

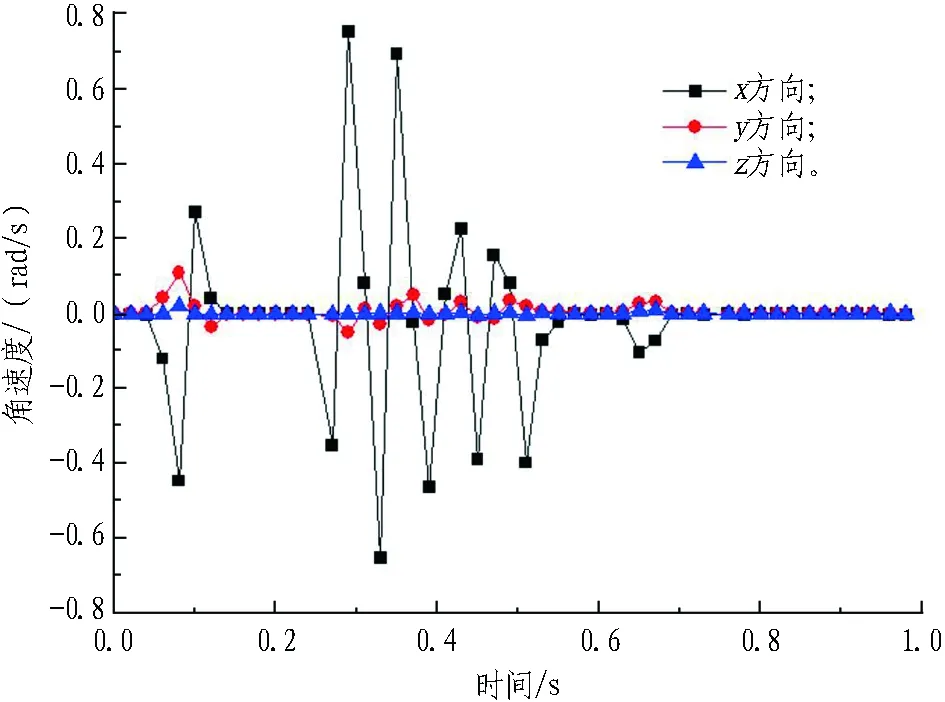
图7 椭球状石碴角速度(Sf=0.72)

Fig. 7 Angular velocities of a pebble with axiolitic shape(Sf=0.72)

扁平状石碴角速度(Sf=0.37)如图8所示。从图8可以看出： 石碴的x、y、z3个方向的角速度均不大，x和z方向几乎为0，y方向角速度为0～0.01 rad/s。由此可得扁平状石碴几乎不做旋转运动，只随拖曳力的增大沿管道轴线运动。

图8 扁平状石碴角速度(Sf=0.37)

2种石碴合角速度和运动速度如图9和图10所示。从图中可以看出： 2种石碴在起动之前的运动状态不一样，椭球状石碴做一定程度的旋转运动，而扁平状石碴几乎处于静止状态。

图9 2种石碴合角速度

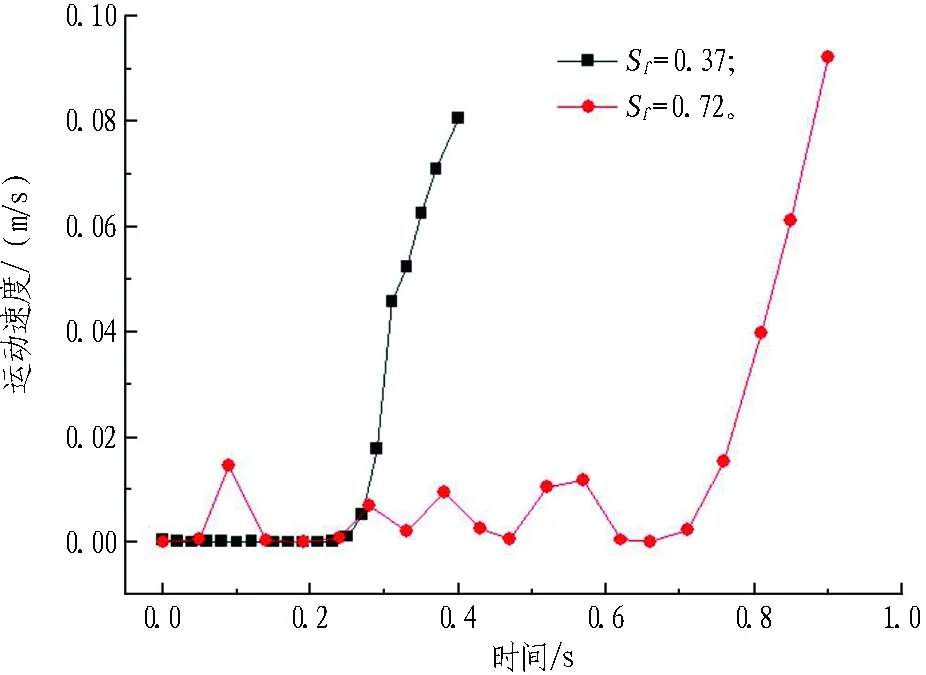
图10 2种石碴运动速度

石碴总共分为3种不同的起动状况。当石碴形状为扁平状时，石碴的运动形式为推移运动；当石碴形状为椭球状时，石碴在起动之前做一定程度的旋转运动，到达起动速度时以推移形式运动；当石碴形状为近球形时，石碴的运动形式为滚动，因为滚动摩擦因数相比于滑动摩擦因数是较小的，所以近球形石碴起动速度相比于扁平状和椭球体石碴要小。因论文研究的石碴等容粒径较大，达到38.5 mm，无法在泥浆浮力和湍流作用下克服重力做悬浮运动，一般是在管道底部做推移运动，而当石碴形状系数达到0.8以上时，会以滚动为主要的运动形式。

3.2 等容粒径对石碴起动速度的影响

为研究等容粒径对石碴颗粒起动速度的影响，在管道内放置形状系数为0.4、不同等容粒径的石碴，其石碴三轴线尺寸如表2所示。

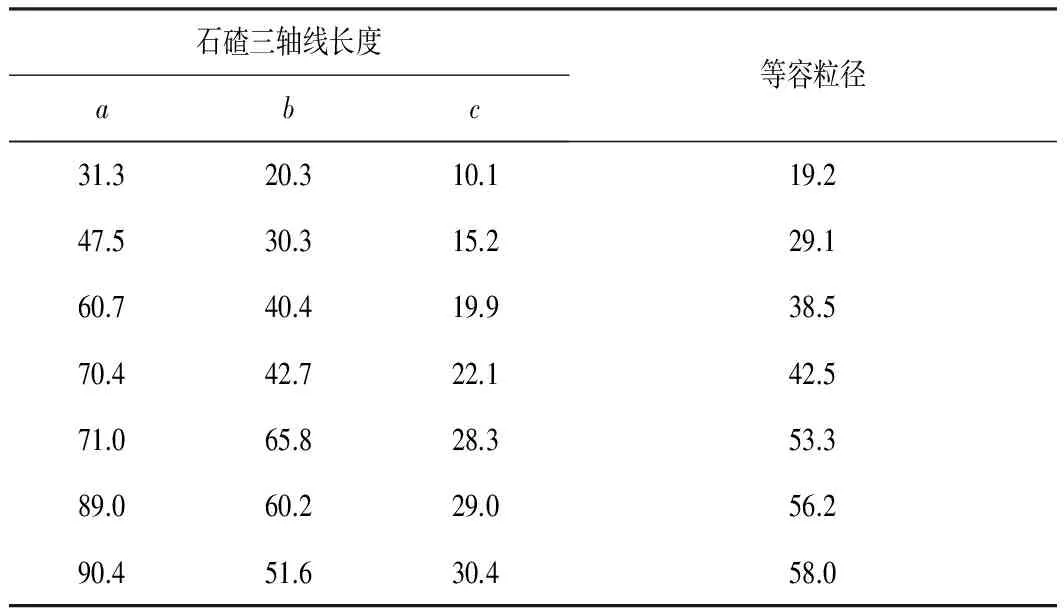
表2 石碴三轴线尺寸

不同等容粒径石碴运动速度如图11所示。由图11可知： 当石碴等容粒径Dv为19.2～38.5 mm时，石碴运动速度曲线近乎重合。

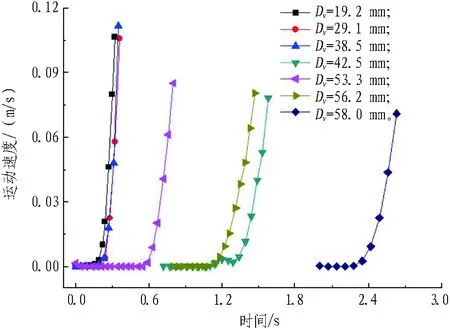
图11 不同等容粒径石碴运动速度

Fig. 11 Velocity of a pebble with differdnt equal volume particle sizes

不同等容粒径石碴起动速度如图12所示。由图12可知： 当石碴等容粒径较小时，石碴起动速度几乎相等；当石碴等容粒径Dv为38.5、42.5、53.3、56.2、58 mm时，石碴起动速度vi为0.48、1.06、1.26、2.36、4.70 m/s，相邻等容粒径间石碴起动速度增幅为120.8%、18.9%、87.3%、99.2%，石碴起动速度随等容粒径的增大呈指数增大，当石碴等容粒径小于38.5 mm时影响不明显，这是因为随着石碴等容粒径的增大，石碴和管壁之间的摩擦阻力越大，所需拖曳力也越大，同时拖曳力与泥浆和石碴的速度差的二次方成正比，石碴初始状态是静止在管壁底部，其速度为0 m/s，即拖曳力与泥浆速度的二次方成正比，当石碴等容粒径较小时，所需拖曳力也较小，所以等容粒径较小时石碴起动速度相差不大，当等容粒径增大到一定程度时，推动石碴进行运动所需拖曳力明显增大，并随着等容粒径的进一步增大呈上升趋势。

图12 不同等容粒径石碴起动速度

Fig. 12 Pickup velocities of a pebble with different equal volume particle sizes

3.3 数量对石碴起动速度的影响

不同数量下石碴运动速度如图13所示，不同数量下石碴起动速度如图14所示。在管道入口一定距离处放置1、20、40、60、80个石碴，单个石碴的三轴尺寸为61.4 mm×41.5 mm×20.3 mm，石碴形状系数为0.4，等容粒径Dv=39.1 mm。由图13可知： 当石碴数量N=1、20、40、60、80时，石碴起动速度vi=0.58、2.76、3.34、3.54、4.26 m/s；单石碴和多石碴起动速度差距很大，N=20时石碴起动速度相比N=1时，增幅达到376%；随着石碴数量的继续增多，石碴起动速度增幅变得平缓，N=20、40、60、80时，相邻之间石碴起动速度增幅分别为21%、6%，20%。由图14可知： 石碴起动速度随石碴数量的增大呈对数增长。

泥水管道内石碴排列如图15所示。由图15可知： 石碴在管道中多以平铺和斜靠方式排列，石碴间相互嵌套比较普遍，随着石碴数量增多，石碴所受摩擦阻力越大，起动时需要克服较大的石碴与石碴之间的相互作用力，所以推动石碴进行运动所需时间越长。

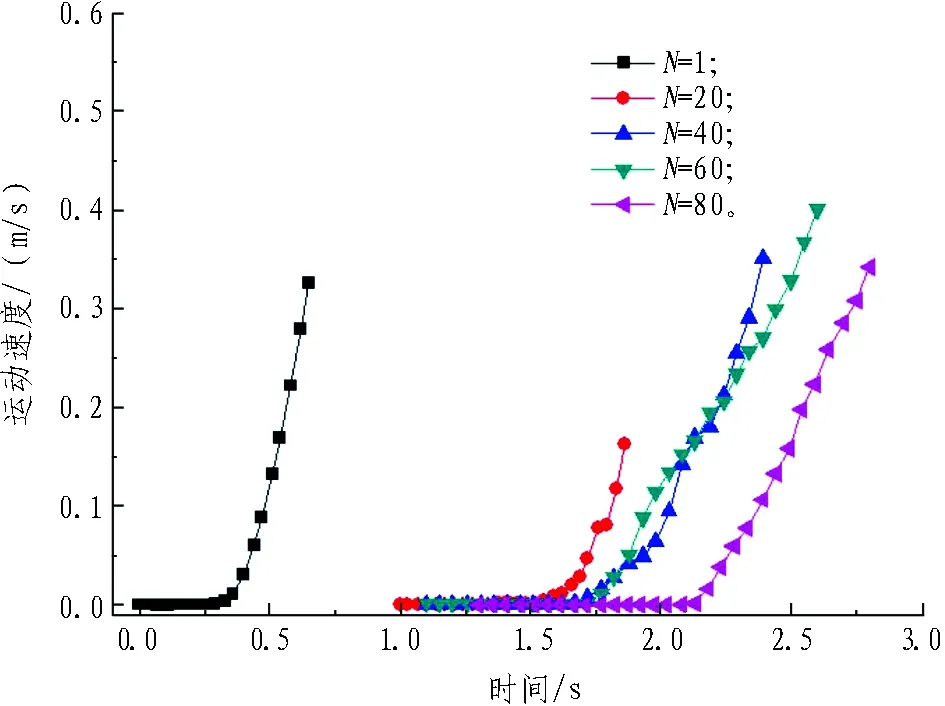
图13 不同数量下石碴运动速度

图14 不同数量下石碴起动速度

(a) 平面图(b)横断面

图15泥水管道内石碴排列平面、横断面示意图

Fig. 15 Sketch diagram of plan and elevation of configuration of pebbles in slurry pipe

4 结论与讨论

文章结合计算流体力学和离散单元法建立了泥水盾构环流系统中水平直管内石碴运动模型，研究石碴形状系数、等容粒径和数量对石碴起动速度的影响，主要结论如下：

1)在石碴等容粒径相等情况下，不同形状石碴起动速度大小顺序为： 椭球体>扁平状>近球形。当石碴形状为扁平状和近球形时，石碴起动速度较低；当石碴形状为椭球体时，在达到起动速度之前做一定程度的旋转运动，起动速度相比扁平状时出现跃变，当Sf=0.55相比Sf=0.37时，石碴起动速度达到1.4 m/s，增幅达到204%。

2)石碴起动速度随等容粒径的增大呈指数增大，当石碴等容粒径小于38.5 mm时影响不明显，其石碴起动速度在0.48 m/s左右；当石碴等容粒径为42.5～58.0 mm时，石碴起动速度随等容粒径增大呈上升趋势。

3)石碴起动速度随石碴数量的增多呈对数增长，单石碴和多石碴起动速度差距很大，N=20时石碴起动速度相比N=1时，增幅达到376%；多石碴起动速度增幅较为平缓，相邻数量石碴起动速度最大增幅发生在N为20～40时，达到21%。

4)后续工作应考虑研究一定体积分数(5%左右)的非球形石碴的起动速度，确定最佳的输送速度，避免不必要的能量损耗。

：

[1] MIN Fanlu, ZHU Wei, LIN Cheng, et al. Opening the excavation chamber of the large-diameter size slurry shield: A case study of Nanjing Yangtze River Tunnel in China[J]. Tunnelling and Underground Space Technology, 2015, 46: 18.

[2] LIU Chao, ZHANG Zixin, Richard A, et al. Pile and pile group response to tunneling using a large diameter slurry shield: Case study in Shanghai[J]. Computers and Geotechnics, 2014, 59: 21.

[3] PAINTAL A S. Concept of critical shear stress in loose boundary open channels[J]. Journal of Hydraulic Research, 1971, 9(1): 91.

[4] BUFFINGTON J M, MONTGOMERY D R. A systematic analysis of eight decades of incipient motion studies with special reference to gravelbedded rivers[J]. Water Resources Research, 1997, 33(8): 1993.

[5] 刘明潇, 孙东坡, 王鹏涛, 等. 双峰型非均匀沙粗细颗粒相互作用对推移质输移的影响[J]. 水利学报, 2015(7): 819.

LIU Mingxiao, SUN Dongpo, WANG Pengtao, et al. Interactions between the coarse and fine particles and their influences on the bimodalnon-uniformbed load transport[J]. Journal of Hydraulic Engineering, 2015(7): 819.

[6] 王继红, 王树刚, 张腾飞, 等. 水平管道内冰浆流动阻力特性实验研究[J]. 哈尔滨工程大学学报, 2014(2): 161.

WANG Jihong, WANG Shugang, ZHANG Tengfei, et al. Experimental investigation into the properties of flowing resistance of ice slurry inside a horizontal pipeline[J]. Journal of Harbin Engineering University, 2014(2): 161.

[7] 曹斌, 徐心一, 夏建新. 水力输送管道中粗颗粒运动状态变化及其判别[J]. 应用基础与工程科学学报, 2016(4): 672.

CAO Bin, XU Xinyi, XIA Jianxin. Movement status change of course particles and its discriminant parameter in hydraulic transporting pipeline[J]. Journal of Basic Science and Engineering, 2016(4): 672.

[8] JIN Baosheng, TAO He, ZHONG Wenqi. Flow behaviors of non-spherical granules in rectangular hopper[J]. Chinese Journal of Chemical Engineering, 2010, 18(6): 931.

[9] 周知进, 刘爱军, 夏毅敏, 等. 颗粒组分特性对扬矿硬管输送速度的影响[J]. 中南大学学报(自然科学版), 2011, 42(9): 2692.

ZHOU Zhijin, LIU Aijun, XIA Yimin, et al. Influence of particles component properties on transporting speed in lifting pipeline[J]. Journal of Central South University (Science and Technology), 2011, 42(9): 2692.

[10] ZHAO T, DAI F, XU N, et al. A composite particle model for non-spherical particles in DEM simulations[J]. Granular Matter, 2015, 17: 763.

[11] AKHSHIK Siamak, BEHZAD Mehdi, RAJABI Majid. CFD-DEM simulation of the hole cleaning process in a deviated well drilling: The effects of particle shape[J]. Particuology, 2016, 25: 72.

[12] 张芝永, 刘光生, 曾剑. 波浪作用下海底管线局部冲刷临界条件[J]. 哈尔滨工程大学学报, 2015, 36(11): 1433.

ZHANG Zhiyong, LIU Guangsheng, ZENG Jian. Critical conditions of local scour below submarine pipelines under wave action[J]. Journal of Harbin Engineering University, 2015, 36(11): 1433.

[13] 陶贺, 金保昇, 钟文琪. 不同物性对椭球形颗粒在移动床中流动特性影响的模拟研究[J]. 中国电机工程学报, 2011(5): 68.

TAO He, JIN Baosheng, ZHONG Wenqi. Effect of particle properties on the flow behaviors of ellipsoidal particles in the moving bed[J]. Proceedings of the CSEE, 2011(5): 68.

[14] 宋晓阳, 及春宁, 许栋. 明渠湍流边界层中颗粒的运动与分布[J]. 力学学报, 2015(2): 231.

SONG Xiaoyang, JI Chunning, XU Dong. Distribution and motion of particles in the turbulent boundary layer of channel flow[J]. Chinese Journal of Theoretical and Applied Mechanics, 2015(2): 231.

[15] JIANG Y Y, ZHANG P. Numerical investigation of slush nitrogen flow in a horizontal pipe[J]. Chemical Engineering Science, 2012, 73: 169.