基于散斑干涉的光滑表面变形快速检测

涂思琪，王永红，孙方圆，高新亚，赵琪涵，闫佩正

(合肥工业大学 仪器科学与光电工程学院，安徽 合肥 230009)

1　引　言

随着现代高新科技产业的迅速发展，对产品零件的加工质量要求日益严格。光滑表面由于具有高反射率、无表面破坏层及低粗糙度等优点，在航空航天、精密机械及光学制造等领域有广泛的应用。随着光滑表面零件在精密制造业所占比重的增大，对光滑产品可靠性和力学性能的检测(如变形/应变测量)也变得愈加重要。实现光滑表面力学性能的无损检测是仪器设备使用安全及寿命预测的基础。

对于光滑表面的测量，早期多使用接触式测量方法，其中以触针式机械扫描法为代表，该方法优点是测量范围大，精度较高，重复性好，但效率低，探针容易磨损，成本高，且极易在表面留下划痕，不适用于弹性或敏感材料的精密测量[1-2]。在这种情况下，非接触式测量方法被提出，并得到快速发展和完善。R S Wriston等将软X射线衍射技术应用于材料的表面结构分析。该方法需要在真空环境下使用，系统复杂，操作繁琐，且只能测量较光滑表面[3-5]。王英姿、侯宪钦提出使用扫描电子显微镜分析钛合金表面形貌，但这种方法测量耗时长，对某些敏感材料会造成辐射损伤，引起二次损害[6]。王肖沐、肖宇彬研究了扫描探针显微镜在材料微观特性检测中的应用:该方法对测量环境要求高[7]，且无法实现大面积测量。高志山、史琪琪将干涉显微镜应用于微观形貌测量，但分辨率受到物镜数值孔径的限制，分辨率仅能达到微米级，无法达到高精度测量要求[8]。以上方法大都属于几何量测量，测量值为高度或形貌，无法直接获取变形/应变等力学性能参数。数字散斑干涉技术能够实现全场高精度变形/应变测量，灵敏度高，在材料缺陷、形貌测量中有广泛应用[9-13]，非常适合于材料和结构的力学性能测量。但该技术主要用于粗糙表面的检测，喷漆等增加表面粗糙度的操作，可能会损坏材料表面性能，不适合于光滑表面物体测量。

本文提出了一种适用于光滑表面的全场变形测量方法，该方法基于改进的数字散斑干涉技术，同时采用空间载波傅里叶变换法[12]，能够实现光滑表面变形的快速动态测量。文中进行了理论分析和光路设计，并组建实验装置进行实验验证，实验结果证明该方法在测量中切实可行。

2　测量原理

光滑表面测量系统结构如图1所示，与传统的数字散斑干涉系统相比，光路中增加了一个透明散射体-毛玻璃。激光通过透明散射体时，在散射体附近的光场中可产生所需的散斑[14]。

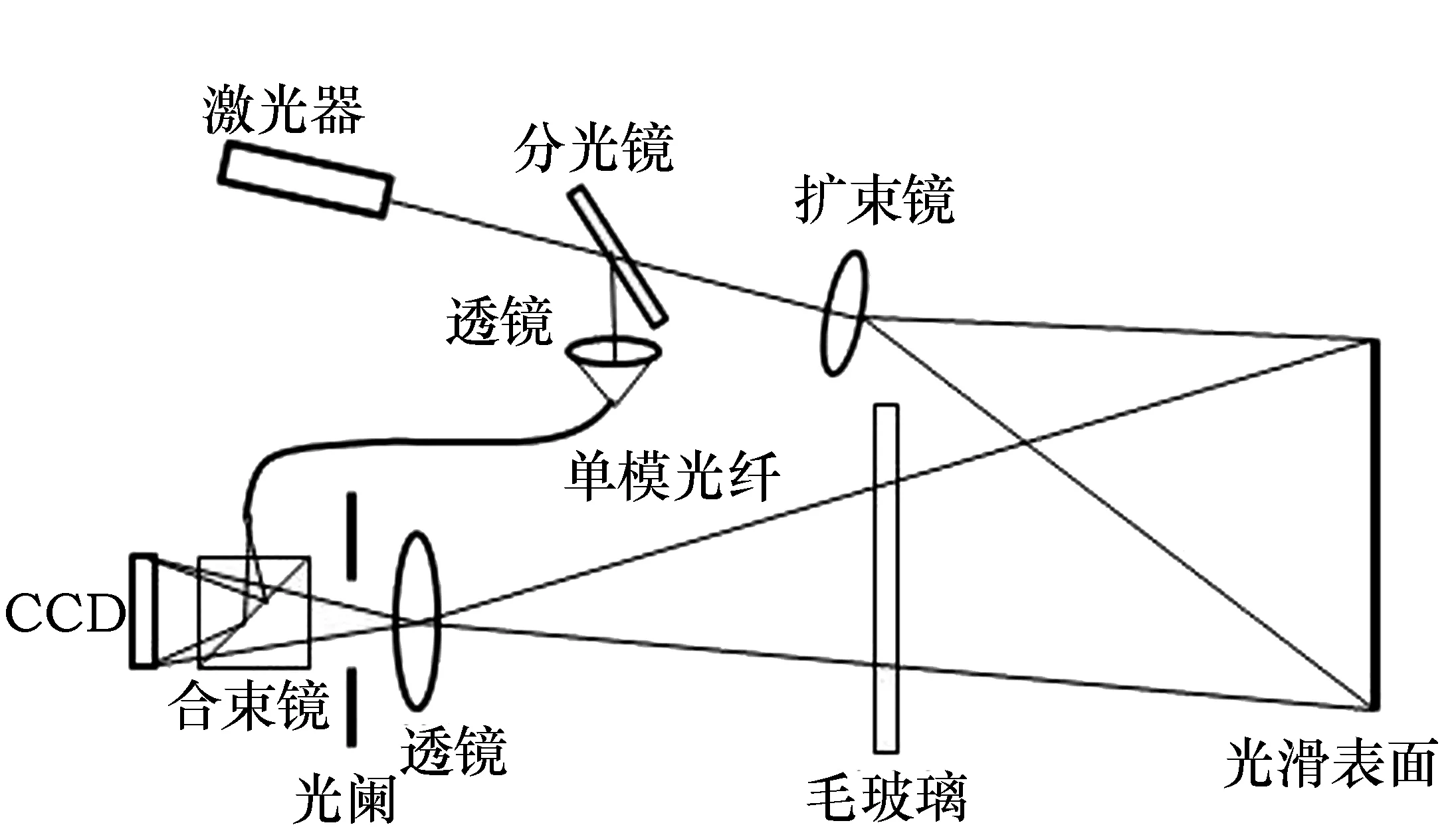
图1　测量系统结构 Fig.1　Structure of measuring system

激光从激光器中出射后，被分光镜分成两束，分别作为物光和参考光。物光被扩束镜扩束，照射在被测光滑表面上，在光滑表面上发生镜面反射，反射光通过毛玻璃产生散斑，经过成像系统和光阑，最终在CCD靶面上成像。而参考光则由透镜汇聚，经单模光纤传输后，通过合束镜进入CCD，与物光在靶面汇合，形成散斑干涉图像，并被CCD相机记录[15]。

设物光为uo(x,y)，参考光为ur(x,y)，它们可表示为

uo(x,y)=|uo(x,y)|exp[iφ(x,y)]

ur(x,y)=|ur(x,y)|exp[-2πifx·x-2πify·y] ,

(1)

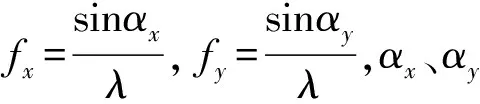
根据干涉原理，CCD相机记录的散斑干涉图像的光强为

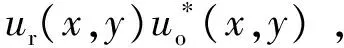
(2)

进行二维傅里叶变换，得到散斑干涉图像的频域信号[16]:

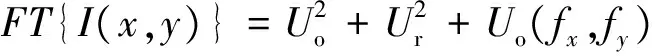
(3)

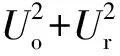
调整参考光的偏转角度，使之以特定角度出射，并引入载波，使得携带相位信息的分量在频域上发生平移。调整载波量(fx,fy)，使相位信息频谱能够与背景光频谱分离。提取相位信息区域，进行傅里叶反变换，得到相位信息φ(x,y)

φ(x,y)+2π(xfx+yfy)=

(4)

分别记录光滑表面变形前后的两幅散斑干涉图像，提取对应的相位信息，进行相减处理后可得到由于表面变形所引起的相位改变量Δ(x,y)[17-18]

Δ(x,y)=φ2(x,y)-φ1(x,y) ,

(5)

其中，φ1(x,y),φ2(x,y)分别代表光滑表面变形前后的相位信息。

表面变形以光的相位变化的形式展现，对于粗糙表面，如图2(a)所示，物体受到加载变形后[19]，表面上的物点S的位置改变为S′,对于小变形，光的相位改变量可表示为:

Δ=(Kr-Ki)·d=K·d,

(6)

式中，Ki、Kr分别代表入射光矢量和反射光矢量，K为灵敏度矢量，d为位移矢量。

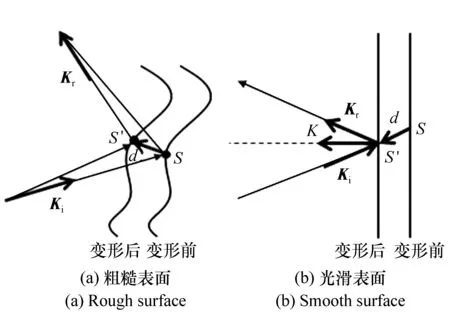
图2　相位变化与位移矢量关系 Fig.2　Relationship between phase changes and displacement vector

但对于光滑表面，如图2(b)所示，光在表面发生镜面反射，根据反射定理Kr·K=-Ki·K，

得到光相位改变量与位移矢量的关系[20]

(7)

根据式(7)可知，相位改变量仅对面外变形分量敏感，并且当观察方向与表面法线方向相同时，灵敏度取得最大值。此时可得到相位改变量与光滑表面的面外变形分量w(x,y)的关系

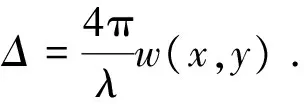
(8)

3　实验与分析

为验证本文方法，进行了验证实验。实验所用的光滑试样为304不锈钢经研磨和抛光加工的8K镜面板，表面光滑平整，镜面效果良好。镜面板大小为120 mm×120 mm。其物理性能参数如表1所示。

表1　304不锈钢物理性能参数

镜面板如图3所示，采用四周螺钉固定，中心采用高精度差动螺旋顶尖加载方式，加载值固定为2 μm。当顶尖进行加载时，镜面板中心将产生一个中心凸起的微小变形。

图3　被测光滑表面 Fig.3　Measured smooth surface

在光学平台上组建实验测量系统(如图4所示)，实验所用光源是波长为532 nm的单纵模绿光激光器，CCD相机采用200万像素的1394工业数字相机。参考光由单模光纤引入，经由合束镜进入CCD相机。

图4　光滑表面测量实验系统 Fig.4　Measurement system of smooth surface

分别采集变形前后的两幅散斑干涉图像，通过空间载波傅里叶变换法提取相位，调整参考光的出射角度和光阑大小，使得相位信息和背景光频谱分离[21]。得到散斑干涉图像的频谱信息如图5所示。

图5　散斑干涉图像频谱信息 Fig.5　Spectrum of speckle interference image

选择相位频谱区域，进行傅里叶反变换，并将两幅散斑干涉图像的相位相减，即可得到由于表面变形所引起的相位差分布，如图6(a) 所示。由于采用了空间载波傅里叶变换法，由单幅图像即可获得全场相移干涉图，无需像传统方法那样采集多幅图像和多步相移，实现了实时快速动态测量。

图6　表面变形引起的相位差分布 Fig.6　Phase difference distribution caused by surface deformation

由于散斑条纹图中含有大量的背景噪声，影响图像后续处理的精确性，因此需要进行滤波处理。常规的滤波算法，如中值滤波、均值滤波及低通滤波等，效果并不理想。中值滤波算法虽能够有效过滤相位条纹图中的脉冲噪声，但当噪声密度较大时，滤波性能较差，尤其对于“尖峰信息”较多的条纹图，中值滤波模糊了条纹的边界细节,时间复杂度高[22]。均值滤波算法简单，运行速度较快，但在去除噪声的同时，容易破坏相位条纹图的突变信息，丢失条纹的边缘细节[23]。低通滤波存在截止频率选择问题，当条纹图的宽度变化较大时，其具有高噪声特点，因此无法区别有用信息和噪声。综合考虑几种滤波算法的去噪性能和条纹图的边界信息保留情况，本文采用基于正余弦变换的频域低通滤波算法。该算法平滑效果较好，在滤除噪声的同时，可有效保留相位条纹图的“尖峰”信息[24]，滤波后的相位如图6(b)所示。

然而，此时的相位范围为[-π，π]，无法反映真实相位信息，因此需要对相位图进行解包裹处理，得到真实相位差分布。

图7　真实相位差分布 Fig.7　Real phase difference distribution

根据式(8)得到相位差与面外变形分量的关系，取λ=532 nm，将解包相位图中各点的相位差Δ(x,y)代入,得到光滑表面变形的真实相位差分布，如图7所示，其图像亮度代表被测物表面高度分布。值得注意的是，本方法计算得到的变形值分辨率极限为：

(9)

式中，N为相位条纹图中像素灰度最大差值。测量范围受成像系统限制，即视场中的每一点在发生变形时，相机中对应的像素点坐标不发生偏移，在实际测试应用中，本实验系统变形的极大值

在10λ以内。

图8所示为本文方法测出的光滑表面的变形场分布结果。根据实验结果可知，8K镜面板的最大变形在中心位置，经过多次重复实验测得，其最大面外变形量分别为1.936、1.861和1.797 μm。该值与高精度差动螺旋加载预设中心变形值2 μm相比，重复性在可允许测量误差范围内。

图8　光滑表面的变形场分布 Fig.8　Deformation distribution of smooth surface

4　结　论

本文提出了一种适用于光滑表面变形测量的新方法，文中以镜面板作为实验对象，进行了测量实验。实验得到了光滑表面的变形场分布图，结果表明最大变形处为镜面板的中央，最大变形量为1.936 μm，与中心变形的预设值相符，验证了该方法的可行性。该方法基于改进的数字散斑干涉技术，不仅具有全场、非接触、高精度和高灵敏度等优点，而且无需对光滑表面进行任何处理，实现了真正意义上的无损检测。相位分布信息的提取采用空间载波傅里叶变换法，由单幅图像即可获得全场相移干涉图，测量速度快，光路设置简单，条纹测量速率与相机帧频同步，能够实现光滑表面变形的快速动态测量。

参考文献：

[1]CHETWYND D G,LIU X,SMITH S T. A controlled-force stylus displacement probe[J].PrecisionEngineering,1996,19(2-3):105-111.

[2]梁嵘,李达成,曹芒,等.表面微观形貌测量及其参数评定的发展趋势[J].光学技术,1998(6):66-68.

LIANG R,LI D CH,CAO M,etal.. Measurement and characterization tendency of the surface microtopography[J].OpticalTechnology,1998(6):66-68.(in Chinese)

[3]WRISTON R S,FROECHTE J F. Soft X-ray scattering by optical surfaces[J].JournaloftheOpticalSocietyofAmerica,1972,62(11):1399-1400.

[4]尼启良,陈波.散射法表面粗糙度测量[J].光学 精密工程,2001,9(2):151-154.

NI Q L,CHEN B. Measurement of surface roughness by sattering method[J].Opt.PrecisionEng.,2001,9(2):151-154.(in Chinese)

[5]陈淑妍,齐立红,陈波.光学散射法表面特征的测量与分析[J].红外与激光工程,2006,35(1):82-85.

CHEN SH Y,QI L H,CHEN B. Measurement and analysis of surface profiles by optical scattering method[J].InfraredandLaserEngineering,2006,35(1):82-85.(in Chinese)

[6]王英姿,侯宪钦.带能谱分析的扫描电子显微镜在材料分析中的应用[J].工艺与检测,2007(9):80-83.

WANG Y Z,HOU X Q. Application of SEM with EDX in material analysis[J].TechnologyandTest,2007(9):80-83.(in Chinese)

[7]王肖沐,肖宇彬,许建斌.扫描探针显微镜在石墨烯研究中的应用[J].电子显微学报,2012,31(1):74-86.

WANG X M,XIAO Y B,XU J B. Graphene with scanning probe microscopy:a review[J].JournalofChineseElectronMicroscopySociety,2012,31(1):74-86.(in Chinese)

[8]史琪琪,高志山,王帅,等.基于白光干涉的微观轮廓复原技术研究[C].全国光学测试学术交流会. 2014.

[9]WANG Y,WU S,YANG L. Synchronous measurement of three-dimensional deformations by multicamera digital speckle patterns interferometry[J].OpticalEngineering,2016,55(9):091408.

[10]LI J R,XIE X,YANG G B,etal.. Whole-field thickness strain measurement using multiple camera digital image correlation system[J].Optics&LasersinEngineering,2017,90:19-25.

[11]王永红,冯家亚,王鑫,等.基于狭缝光阑的剪切散斑干涉动态测量[J].光学 精密工程,2015,23(3):645-651.

WANG Y H,FENG J Y,WANG X,etal.. Shearing speckle interferometry based on slit aperture for dynamic measurement[J].Opt.PrecisionEng.,2015,23(3):645-651.(in Chinese)

[12]孙永建,孙晓明,刘云起,等.基于线性扩散板的高光抑制方法研究[J].液晶与显示,2016,31(9):897-901.

SUN Y J,SUN X M,LIU Y Q,etal.. Specular highlight suppression method based on linear diffuser[J].ChineseJournalofLiquidCrystalsandDisplays,2016,31(9):897-901.(in Chinese)

[13]王永红,吕有斌,高新亚,等.剪切散斑干涉技术及应用研究进展[J].中国光学,2017,10(3):300-309.

WANG Y H,LV Y B,GAO X Y,etal.. Research progress in shearography and its applications[J].ChineseOptics,2017,10(3):300-309.(in Chinese)

[14]田青,王辉,任志君.数字全息再现像的激光散斑消除的研究[J].应用激光,2006,26(6):439-442.

TIAN Q,WANG H,REN ZH J. Reduction of speckle noise in digital holography[J].AppliedLaser,2006,26(6):439-442.(in Chinese)

[15]刘佩,王永红,冯家亚,等.偏转角空间载波相位检测技术[J].光电工程,2015,42(3):39-43.

LIU P,WANG Y H,FENG J Y,etal.. Phase detection technology in spatial carriar based on deflection angle[J].Opto-ElectronicEngineering,2015,42(3):39-43.(in Chinese)

[16]LI J R,XU W,XIE X,etal.. Experimental study of FLD0 for aluminum alloy using digital image correlation with modified ISO method[J].InternationalJournalofMaterialsResearch,2016,107(3):245-253.

[17]杨连祥,祝连庆,谢辛,等.电子散斑干涉测量中相移技术的新发展[J].北京信息科技大学学报(自然科学版),2013(2):1-8.

YANG L X,ZHU L Q,XIE X,etal.. New development of phase-shift techniques in electronic speckle pattern interferometry[J].JournalofBeijingInformationScienceandTechnologyUniversity,2013(2):1-8.(in Chinese)

[18]汪相如,贺晓娴,方琳,等.傅立叶1/4波片法检测液晶光学相控阵移相量的精度分析[J].液晶与显示,2017,32(1):7-12.

WANG X R,HE X X,FANG L,etal.. Precision analysis on the phase delay measurement method of Fourier quarter-wave-plate on liquid crystal optical phased array[J].ChineseJournalofLiquidCrystalsandDisplays,2017,32(1):7-12.(in Chinese)

[19]蔡长青.散斑干涉计量关键问题研究及其应用[D].广州:华南理工大学,2013

CAI CH Q. The research of key issues in speckle interferometry measurement and its application[D]. Guangzhou:South China University of Technology,2013.(in Chinese)

[20]HANSEN R S. A compact ESPI system for displacement measurements of specular reflecting or optical rough surfaces[J].Optics&LasersinEngineering,2004,41(1):73-80.

[21]LI J,XIE X,YANG G,etal.. Whole-field thickness strain measurement using multiple camera digital image correlation system[J].Optics&LasersinEngineering,2017,90:19-25.

[22]刘国宏,郭文明.改进的中值滤波去噪算法应用分析[J].计算机工程与应用,2010,46(10):187-189.

LIU G H,GUO W M. Application of improved arithmatic of median filter denosing[J].ComputerEngineeringandApplications,2010,46(10):187-189.(in Chinese)

[23]朱士虎,游春霞.一种改进的均值滤波算法[J].计算机应用与软件,2013,30(12):97-99,116.

ZHU SH H,YOU CH X. A modified average flitering algorithm[J].ComputerApplicationandSoftware,2013,30(12):97-99,116.(in Chinese)

[24]王永红,李骏睿,孙建飞,等.散斑干涉相位条纹图的频域滤波处理[J].中国光学,2014,7(3):389-395.

WANG Y H,LI J R,SUN J F,etal.. Frequency domain flitering for phase pattern of digital speckle pattern interferometry[J].ChineseOptics,2014,7(3):389-395.(in Chinese)