克林贝格摆线锥齿轮建模及模态分析

张华,何卫东,张迎辉

(大连交通大学 机械工程学院，辽宁 大连 116028)

0　引言

摆线锥齿轮是一种重要的机械传动零件，它具有承载能力强，传动平稳，噪声小的优点，广泛应用于飞机，航空，船舶，汽车等传动装置中.目前孙中飞[1]等人对螺旋锥齿轮采用球面渐开线理论实现齿面曲线分段参数化，并用NURBS方法拟合建模，但没有考虑实际齿轮加工.许春香[2]等人开发了摆线锥齿轮几何尺寸和加工调整参数的计算模块.汤兆平[3]等人结合齿线长幅外摆线展成线和齿廓球面渐开线推导其曲线方程并建模.张志民[4]等人做模态分析，得到10阶固有频率.

本文从摆线锥齿轮的切齿加工出发，结合齿轮啮合原理推导出齿面方程，建立三维模型.运用有限元处理软件对摆线锥齿轮进行模态分析，计算齿轮啮合的临界转速，为摆线锥齿轮进一步进行动力学研究及结构优化打下基础.

1　摆线锥齿轮三维建模

1.1　刀刃方程

克林贝格摆线锥齿轮的加工采用展成法连续分度双面铣齿加工，加工时没有刀盘倾斜，加工出来的齿轮是等高摆线锥齿轮，齿线是标准的延伸外摆线.它的加工原理是采用假想平面齿轮原理，刀盘转过一组刀片，产形轮也转过一个齿，刀盘绕自身的轴线自转并且绕产形轮轴线公转.现在以大齿轮凸面为例.

刀盘坐标系如图1所示.坐标系So固连在刀盘上，面对刀盘，坐标系zo轴与刀盘轴重合，并且指向朝为zo轴的正方向，xo-yo平面通过刀齿节点并垂直于刀盘轴线.由图中的几何关系可以得到刀刃上任意点在坐标系So中的矢量方程为：

(1)

其中，齿形角与齿轮法向压力角相等都是αn，δo是刀齿方向角;m是分度圆平面内的参考点;u是刀齿上任意一点到参考点m的距离;θo是刀盘自转角度，规定逆时针旋转为“+”，则顺时针旋转为“-”.

图1　刀盘坐标系

1.2　产形面方程

产形轮坐标系如图2所示.从刀盘坐标系So到摇台坐标系Sm的坐标变换矩阵为：

(2)

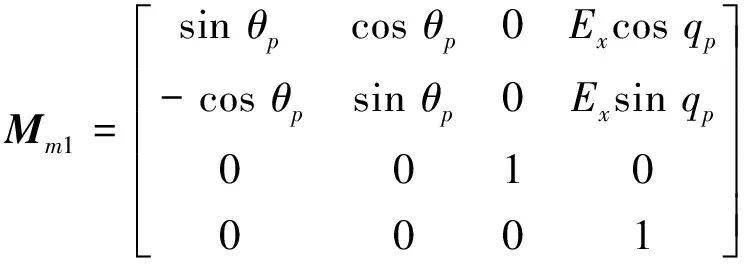
(3)

其中，βm是参考点处的螺旋角;Ex是齿轮径向刀位;qp是齿轮角向刀位;θp是刀盘公转的角度，与刀盘自转角度θo的关系是：

(4)

其中，zo是刀盘的刀片组数;zp是冠轮的齿数;ipo是刀盘的刀片组数与冠轮齿数之比.

产形轮的产形面的齿面方程为下式：

rp(θo,u)=Mm1M1or(θo,u)

(5)

图2　产形轮坐标系

1.3　铣齿加工坐标系及其方程

铣齿加工坐标系如图3所示，铣齿加工右旋大齿轮时，从摇台正面看过去，摇台是逆时针转动，从轮坯的小端看过去，轮坯是顺时针转动.

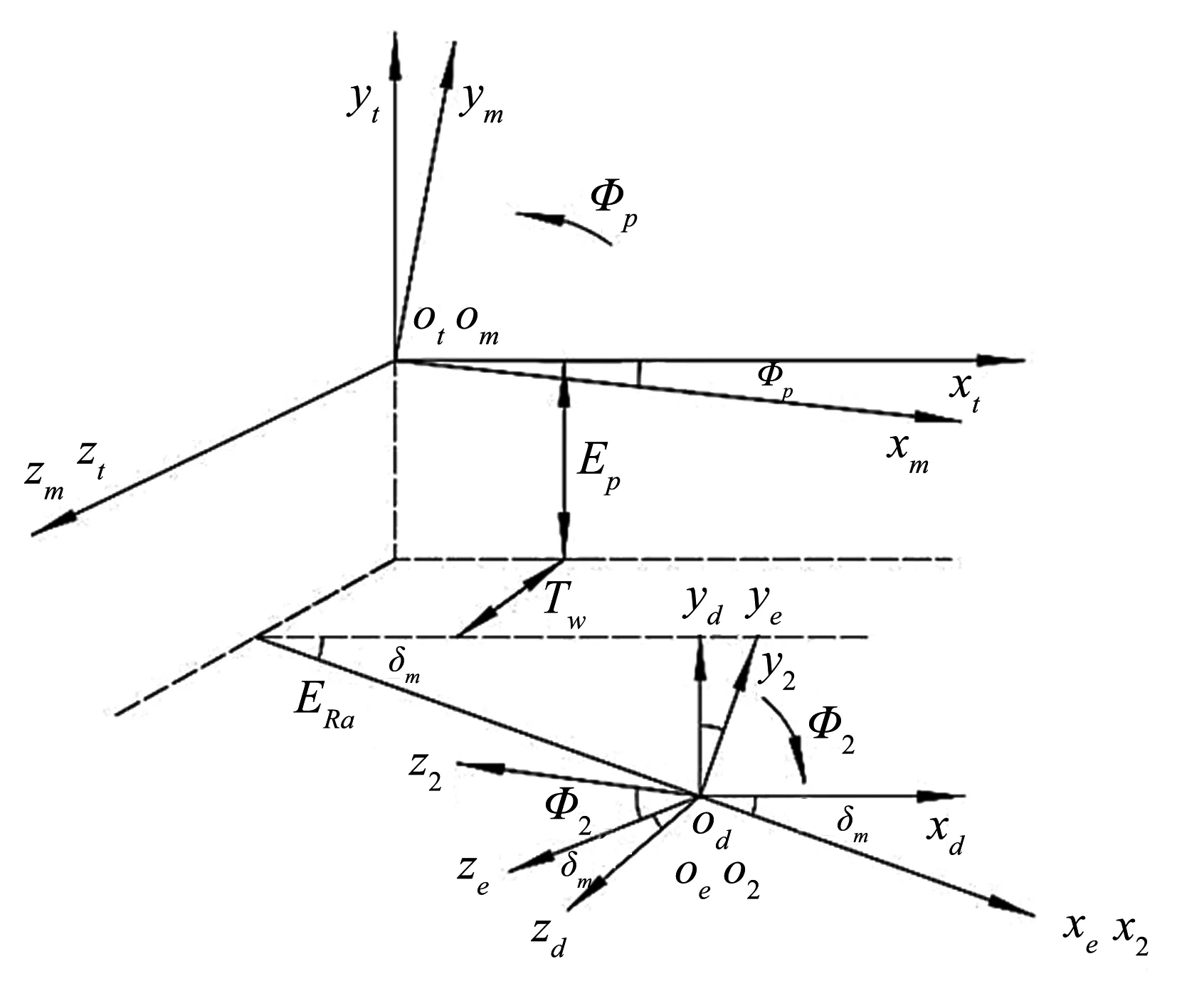
图3　铣齿加工坐标系

建立机床固定坐标系St，坐标系St与机床固连，坐标轴zt与摇台坐标轴zm重合并且方向相同.建立辅助固定坐标系Sd，坐标系通过齿轮顶点，坐标轴zd与坐标轴zt平行且方向相同.建立辅助固定坐标系Se，坐标原点Oe辅助坐标系Sd的原点Od重合.建立轮坯动坐标系S2，坐标系可以绕坐标轴x2旋转.

从摇台坐标系Sm到机床坐标系St的坐标变换矩阵为：

(6)

(7)

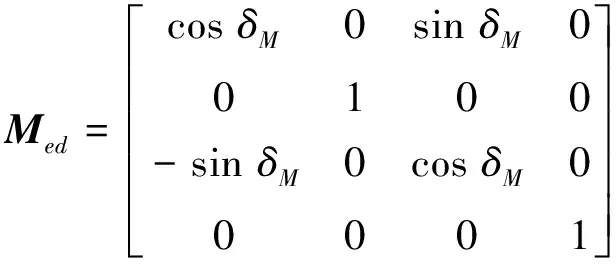
(8)

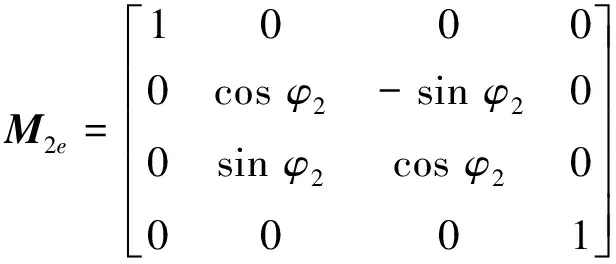
(9)

其中，φp是摇台转过的角度;ERa是轴向轮位;Ep是垂直轮位;TW是床位;δM是轮坯安装角;zp是冠轮的齿数;z2是被加工齿轮的齿数;i2p是冠轮齿数与被加工齿轮的齿数之比;φ2是轮坯转过的角度，与摇台转过的角度φp的关系关系是

(10)

通过空间几何坐标变换得到的铣齿加工的方程数学表达式描述为下式：

1.4　齿面方程

在机床坐标系St下的产形轮齿面方程为：

rt(φp,θo,u)=Mtm(φp)Mm1M1or(θo,u)

(12)

产形轮的单位法矢量为：

(13)

克林贝格摆线锥齿轮大、小齿轮均采用展成法加工，只需要把相对应的机床调整进行改变就可以得到小齿轮的齿面方程.

由齿轮的啮合原理得到：

(14)

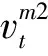
联立方程得到齿面方程为：

(15)

1.5　齿面点计算

摆线锥齿轮的齿轮轴截面作旋转投影平面，如图4所示.把齿轮旋转投影平面平均划分为网格，坐标原点为齿轮轮坯的分锥顶点.齿面上的任意点坐标值为：

(16)

其中，xD，yD是图中D点的坐标值，沿齿线方向(DA方向)分n份，沿齿高方向(DC方向)分m份，网格节点的序号为：i=1,2,…,m，j=1,2,…,n，Δxi、Δyi、Δxj、Δyj分别表示任意点在DA方向和DC方向上坐标的增量，则：

(17)

其中，h是齿高，b是齿宽.

图4　齿面旋转投影平面

齿面坐标值与旋转投影平面内的坐标值的关系为：

(18)

其中，x、y、z就是齿面在空间的点坐标值.

由式(17)和式(15)联立，运用数值计算得到轮坯齿面的离散点坐标值.

1.6　齿轮三维模型建立

将数值模拟法得到的齿面离散点坐标值导入CAD软件，由齿面点坐标值形成齿面网格线，再由齿面网格线生成齿面曲面，将齿面曲面进行剪切缝，然后进行实体化，得到单个齿，如图5所示，旋转阵列后建立摆线锥齿轮的实体模型.

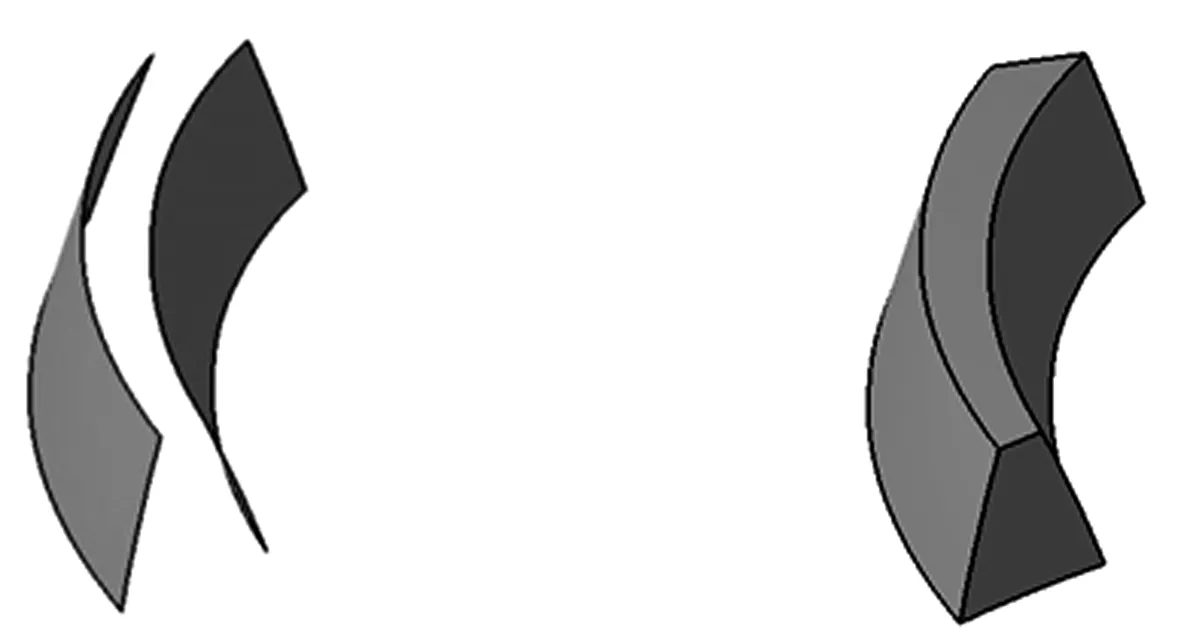
图5　齿面曲面及单齿实体

建立一对啮合摆线锥齿轮，齿轮的相关几何参数如下：左旋小齿轮齿数z1=24，为主动齿轮；右旋大齿轮齿数z2=49，为被动齿轮；中点法向模数mn=6.5 mm；法向压力角αn=20°；中点螺旋角βm=35°；齿宽b=75 mm；齿顶高系数ha*=1；顶隙系数C*=0.25；切向变位系数xt=0.05；径向变位系数x=0.181 4.建立的三维模型如图6所示.

图6　摆线锥齿轮小轮和大轮实体模型

2　摆线锥齿轮模态分析

2.1　有限元模型及约束施加

将CAD建模软件中建好的摆线锥齿轮实体模型导入CAE有限元软件中，进行齿轮模态分析.在有限元前处理器中设置实体单元类型为solid187，采取自动划分网格，小轮划分的网格节点数为8 916 1个，单元数为5 696 3个，大轮划分的网格节点数为11 210 2个，单元数为70 738个.定义摆线锥齿轮的材料属性：弹性模量E=2.06×105MPa，泊松比μ=0.3，材料密度ρ=7 800 kg/m3.

在施加摆线锥齿轮约束时，大齿轮内表面与小齿轮轴外表面施约束，在自由振动状态下求出齿轮各阶的固有特征，不需要施加载荷，有限元约束模型如图7所示.

图7　小齿轮和大齿轮有限元约束模型

2.2　求解及结果分析

在solution下选取modal，在模态分析的分析选项中选取Block lanczos法进行模态提取，低阶模态在结构动力学中起到比较重要的作用，在进行结构振动特性分析时提取前10阶模态，并且将扩展模态打开.经过有限元计算，获得摆线锥齿轮前10阶模态的固有频率及振型，如表1所示.

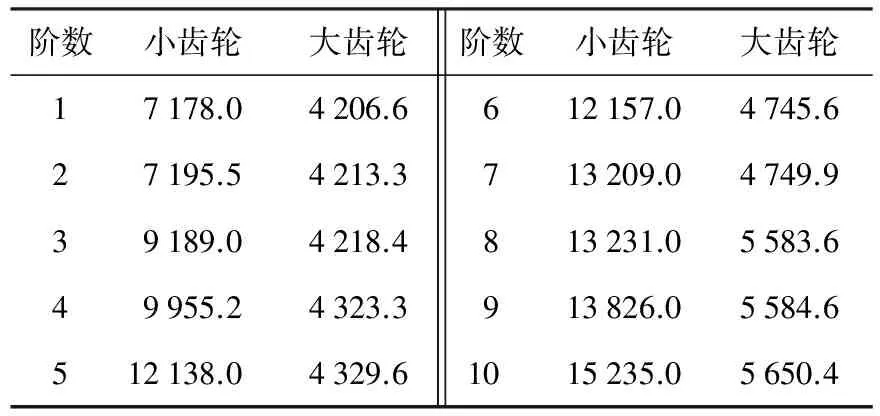
表1　摆线锥齿轮固有频率 Hz

由于篇幅原因，列出小齿轮第3、5、7、9阶主振型图如图8所示，大齿轮第3、5、7、9阶主振型图如图9所示.

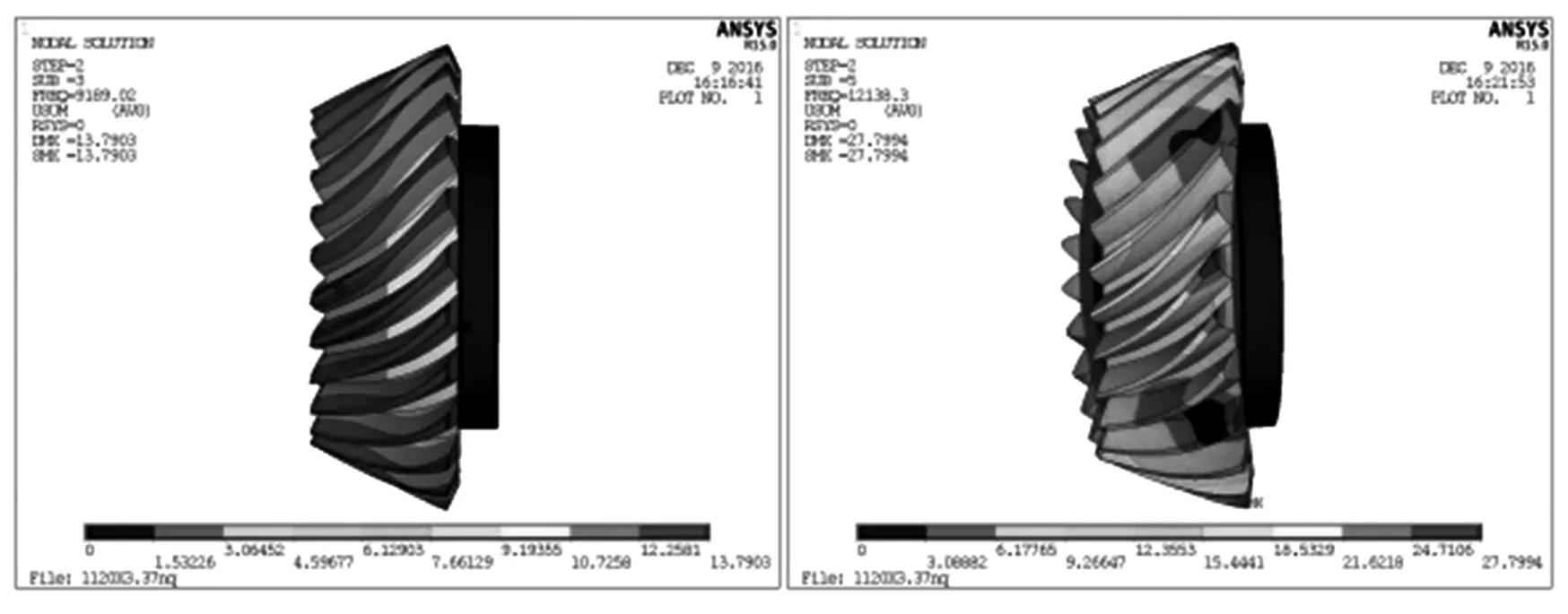
(a) 小齿轮第3、5阶主振型

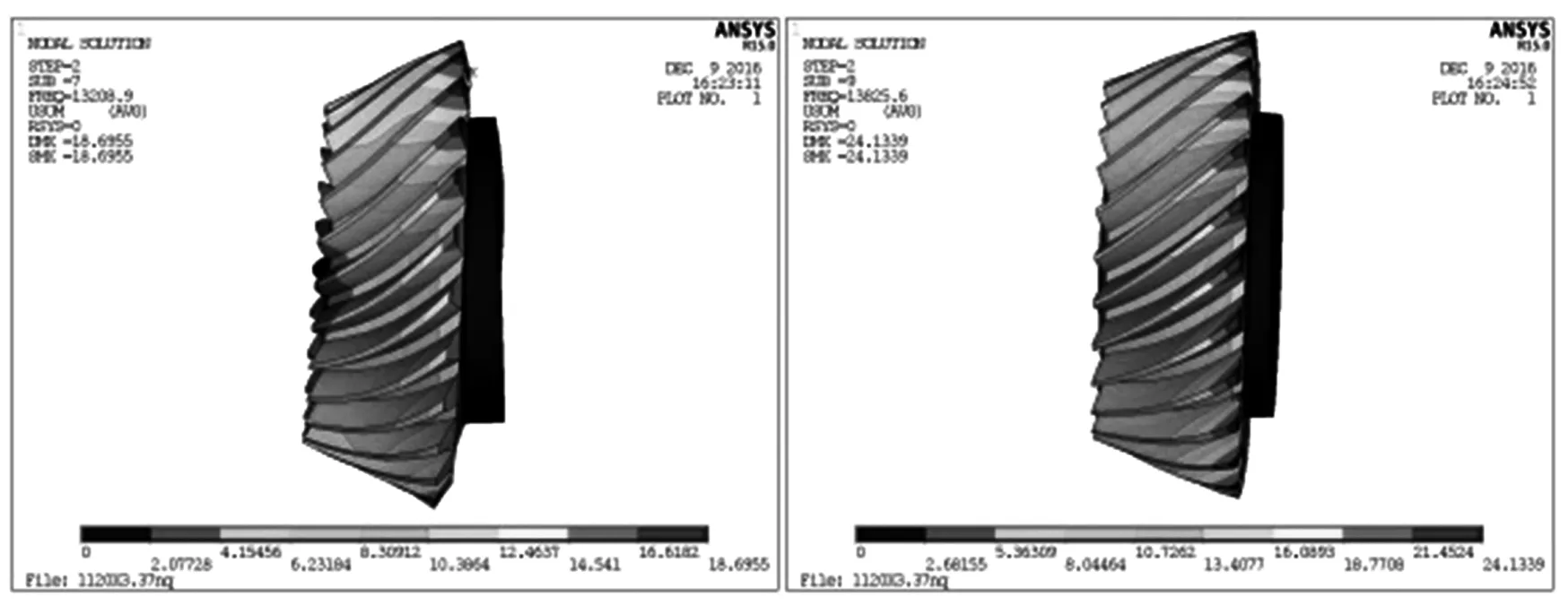
(b) 小齿轮第7、9阶主振型

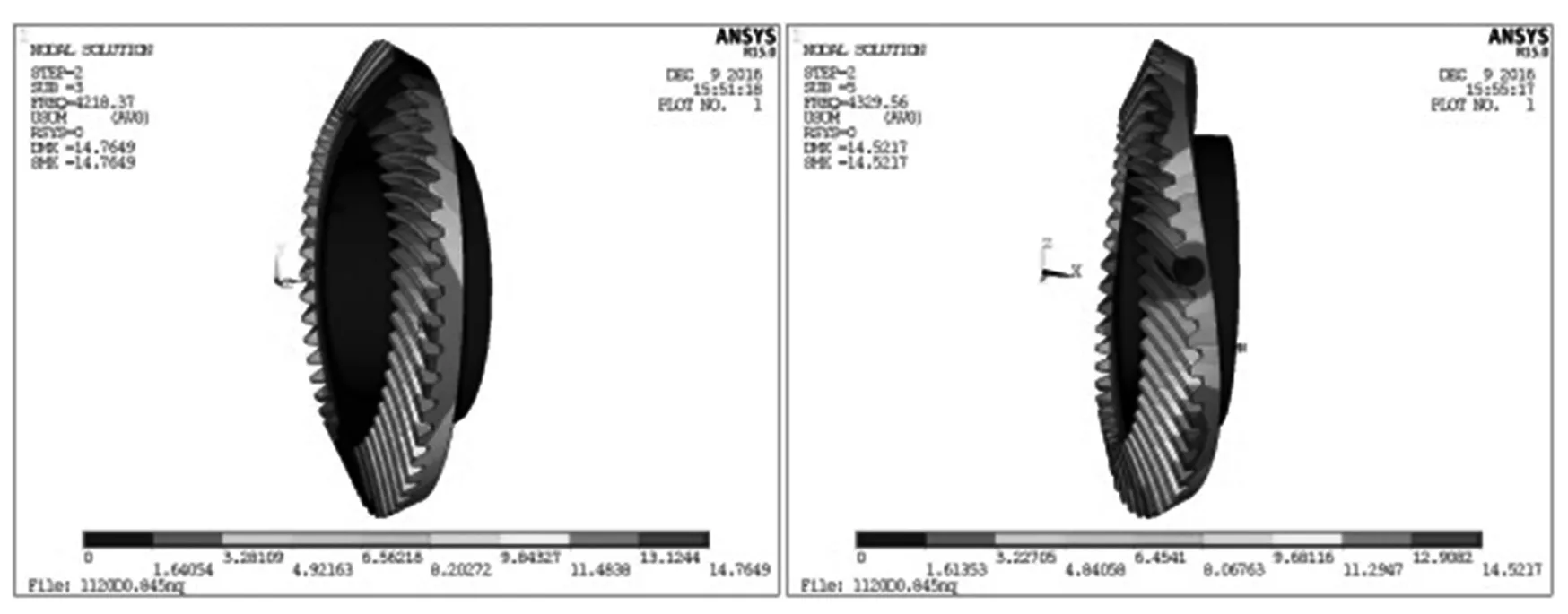
(a) 大齿轮第3、5阶主振型

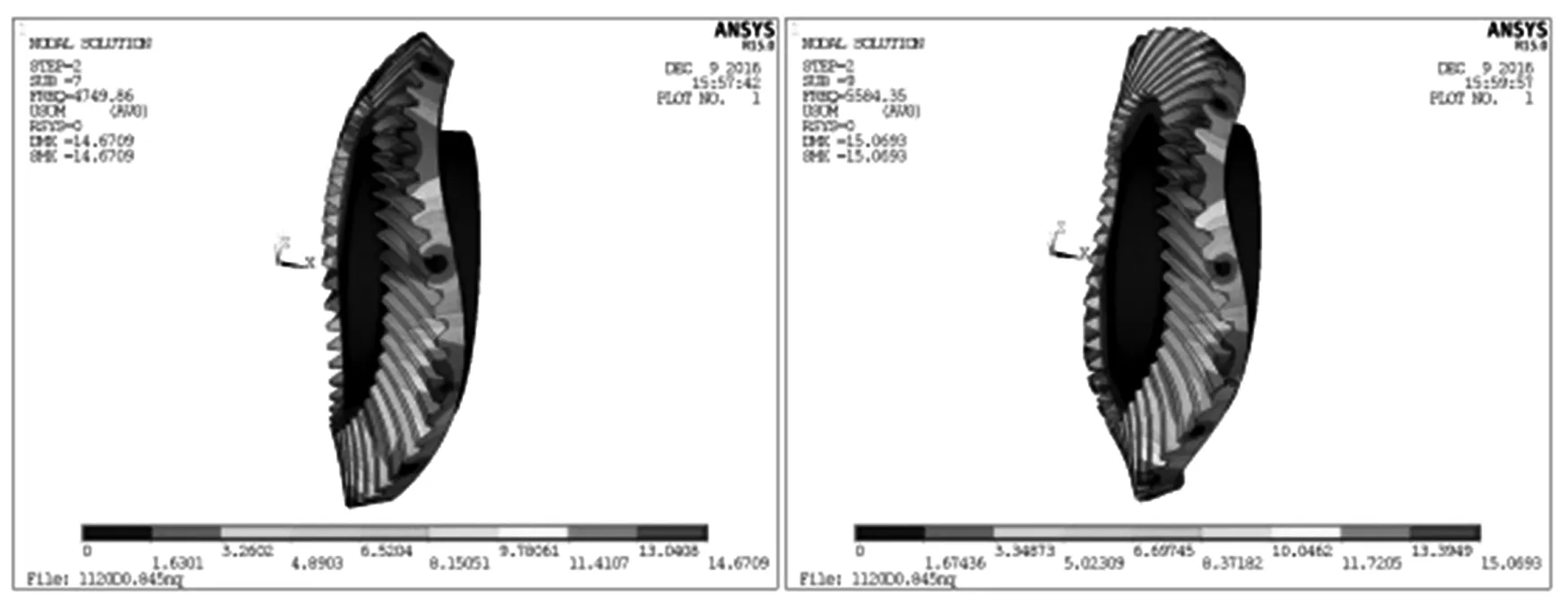
(b) 大齿轮第7、9阶主振型

从表1的模态计算结果可以看出，小齿轮和大齿轮的固有频率都是随着阶数的增加而逐渐增大，小齿轮的固有频率要比大齿轮的固有频率大，并且大齿轮固有频率最小值达到4 000 Hz以上.从模态仿真的振型图结果中可以看到齿轮主振型，在静止状态下有扭转振型，伞型振型，对折振型，圆周振型等，以及最大变形量及最大变形产生的位置等.例如在第5阶模态时，频率是12 138.0 Hz，主振型是对折振型，最大变形量是27.799 4 mm，最大变形量产生在X方向.为了防止系统共振现象的产生，在做齿轮结构设计时，应考虑到主振型并且尽量避开齿轮的固有频率或者固有频率的倍数.

从表1可以知道大齿轮及小齿轮的最低固有频率分别为4 206.6 Hz和7 178 Hz.齿轮副的啮合频率计算公式为：

(19)

式中，fm是啮合频率;ni是输入轴转速;zi是齿轮齿数.

根据公式计算得出，小齿轮临界最低转速是17 945 r/min，大齿轮临界最低转速是5 151r/min.该小齿轮在实际工况中的最大转速为1 969 r/min，从计算结果可以看到小齿轮的临界最低转速远大于实际工况中的转速，大齿轮的临界最低转速较小，但也比其实际工作转速大，因此在正常工作状态下两个齿轮都不会发生共振.

3　结论

(1)根据克林贝格摆线锥齿轮的铣齿加工原理和机床调整参数，用数值模拟的方法得到齿面，从而得到更符合实际的齿轮模型;

(2)对摆线锥齿轮进行模态分析，得到前10阶齿轮固有频率和对应的主振型及变形量，通过齿轮啮合频率计算得到可能发生共振时的理论工作转速，验证了齿轮在正常工作状态下是不会发生共振.

参考文献:

[1]孙中飞,阿达依·谢尔亚孜旦,丁撼.球面渐开线齿形的螺旋锥齿轮NURBS设计[J].工程设计学报,2014,21(3):278- 284.

[2]许春香,邬向伟.摆线齿锥齿轮加工调整计算及程序开发[J].机械传动,2012,36(9):96- 99.

[3]汤兆平,孙剑萍.克林贝格摆线齿锥齿轮的精确参数化建模[J].机床与液压,2010,38(3):113- 116,132.

[4]张志民,樊喜刚,周志刚,等.基于ANSYS的摆线锥齿轮有限元模态分析与研究[J].新技术新工艺,2015(1):100- 102.

[5]王犇,华林.高速旋转状态下汽车弧齿锥齿轮的动力学模态分析[J].汽车工程,2011,33(5):447- 451.