新型磁通补偿型零序滤波器*

李剑桥， 刘 银

广东电网有限责任公司 茂名供电局 广东茂名 525000

1 研究背景

近年来，随着非线性负荷的比重不断增加，电网中出现了频次更加丰富的谐波，由负荷产生的谐波逐渐成为电力系统谐波问题的主要来源[1]。低压配电网直接与用户相连，存在很多不同类型的负载，配电网中的谐波污染是电力系统中最为严重的[2]。三相零序谐波电流是三个幅值相等、相位相同的3次及3倍数次谐波电流[3]，三相零序电流在电网中性线上互相叠加，使中性线上谐波含量很高，中性线上的谐波电流会使系统出现不同程度的过电压，严重时可能造成中性线烧断事故。

针对零序电流的特点，笔者提出了新型磁通补偿型零序滤波器。这是一种绕组采用Z形连接的滤波电抗器，对零序电流呈现低阻特性，从而使零序电流主要流经零序滤波器，而不通过中性线。相比于无源滤波器，这一新型零序滤波器的滤波特性不受系统参数影响，不易出现过负荷、失谐等现象，同时，电抗耐过载能力强。与有源滤波器相比，这一新型零序滤波器结构简单，无复杂控制策略，成本较低。

零序滤波器的滤波效果与其零序阻抗大小密切相关，零序阻抗是工程设计中的重要参数[4]。然而，零序磁通因与空气接触，会形成回路，不固定的磁路利用常规公式又很难精确计算出零序阻抗[5]，给工程设计带来困难。针对以上问题，笔者采用漏磁链解析法及能量法分别对零序阻抗进行计算，通过ANSYS软件仿真验证算法的可靠性，并基于一台400V、100A零序滤波器样机进行验证试验。

2 磁通补偿型零序滤波器结构与原理

新型磁通补偿型零序滤波器绕组的接线方式如图1所示，每相绕组分为两部分，分别位于两个不同的铁芯柱上。将一个铁芯柱的上半绕组与另一个铁芯柱的下半绕组反串起来，组成一相。每个铁芯柱的上下绕组匝数相等，绕组采用Z形连接，下半绕组作为磁通补偿绕组，不同相之间的绕组匝数也相等。电流从每相的上半绕组中流入，将三个下半绕组接在一起后接至电网的中性线上。

由于各相绕组匝数相等，因此采用曲折连接后同一个铁芯柱上下绕组产生的零序励磁磁通大小相等、方向相反，即满足：

(1)

式中：ΨA0、Ψa0分别为A相上下绕组通过的磁通，Wb；ΨB0、Ψb0分别为B相上下绕组通过的磁通，Wb；ΨC0、Ψc0分别为C相上下绕组通过的磁通，Wb。

由式(1)可知，如果流经滤波器的三相电流相等，那么同一铁芯柱上的零序励磁磁通将会相互抵消，使每相串联绕组呈现低阻抗。具有此特性的电流是零序谐波电流，而对于正负序电流而言，因为正负序磁通不能相互抵消，励磁磁阻很大，所以不能通过零序滤波器。

零序滤波器连接在电源和负载之间，实现零序电流的低阻通道，将负载产生的基波不平衡电流、3次及3倍数次谐波电流等零序性质的电流导入，避免零序电流主要成分通过系统形成回路，达到滤波效果。当系统三相电压不平衡时，由此引起的零序电流将很容易通过零序滤波器流入中性线，造成中性线电流过大，因此需在电源与零序滤波器之间增加阻零器，系统等效接线如图2所示。

图2 系统等效电路图

图2中，Vs0(t)为三相不平衡系统零序电压源，is0(t)为不平衡负荷引起的零序电流源，isn(t)为流经零序滤波器的零序电流，Zsf为电源与滤波器间导线的阻抗，Zz为阻零器阻抗，Zzf为零序滤波器阻抗，Zsn为滤波器与电源间中性线的阻抗，ZLn为滤波器与负载间中性线的阻抗。

根据叠加原理，流经零序滤波器的零序电流由两部分组成：

isn(t)=isn1(t)+isn2(t)

(2)

式中：isn1(t)为由is0(t)引起的中性线电流，A；isn2(t) 为由Vs0(t)引起的中性线电流，A。

阻零器加入系统前，由零序电压源Vs0(t)引起的中性线电流为：

(3)

由式(3)可知，虽然Zsf、Zsn、Zzf很小，但是即使很小的零序电压，也会产生很大的零序电流。

阻零器是将三相绕组按同方向缠绕在同一个铁芯柱上而构成的。当A、B、C三相正负序电流通过阻零器时，由于三相电流大小相等，角度相差120°，因此所产生的磁通叠加之和为0，阻零器对其阻抗也为0。当零序谐波电流通过阻零器时，由于零序谐波电流同相位，因此所产生的磁通叠加之和会产生很大的磁通，此时阻零器对零序谐波电流呈现很大的阻抗，从而达到降低零序电流的目的，且对系统正负序分量基本无影响。

3 零序漏磁势分析

由前述分析可知，同一铁芯柱的零序磁通相互抵消，因此零序电抗完全由零序漏电抗组成，并且零序漏电抗远小于系统自身的零序阻抗。零序漏磁通主要通过周围空气及所邻近的部分铁芯柱闭合。图3为零序漏磁势分布图，磁势分布曲线以内绕组线圈内侧延长线与基准线的交点为起点绘制，若磁势增大，则磁势曲线斜向上延伸；若磁势减小，则磁势曲线斜向下延伸。在滤波器内绕组中，磁势沿内径向外正比例增大，因此曲线绘制为斜向上的一条直线。按同样的绘制方法绘制出外绕组的磁势分布线。可见，零序滤波器的漏磁势为一个梯形漏磁组。

图3 零序漏磁势分布

图3中，C1、C2为一个铁芯柱上的两个半绕组，a1、a2分别为内外绕组的截面厚度，a12为内外绕组间的距离，r1、r2分别为内外绕组的平均半径，r12为中间空道的平均半径，h为铁芯柱高度，hc为绕组高度。

4 零序阻抗算法

4.1 解析算法

零序滤波器的漏电抗实质上反映的是漏磁通与绕组线匝交链程度[6]。根据漏磁组，可以采用漏磁链法计算滤波器的零序电抗。计算分为两部分： ① 两线圈之间呈矩形分布的漏磁链，这一部分与内绕组线圈完全交链；② 各绕组产生的呈三角形分布的漏磁势，这一部分磁密分布不均，需进行积分运算。

针对三角形漏磁势部分，在内绕组中距离内边沿x处取一个厚度为dx的小圆薄环，忽略该圆薄环的厚度，该处的漏磁密为xB1/a1，它所交链的绕组匝数为xW1/a1，小圆薄环的漏磁面积为 2π(R+x)dx，因此，该空心圆薄环的漏磁链为：

(4)

式中：B1为三角形部分磁密最大值，T；R为铁芯到内绕组的距离，m；W1为内绕组匝数。

沿径向向内积分，则该绕组总漏磁链为：

(5)

该绕组的总漏磁链用平均半径r1代替R+3a1/4，结果相差不大，则式(5)可以表示为：

φ1=2πB1W1a1r1/3

(6)

同理，外绕组产生的三角形漏磁势所交链的总漏磁链为：

φ2=2πB1W2a2r2/3

(7)

式中：W2为外绕组匝数，W2=W1。

内外绕组之间的矩形漏磁势所产生的漏磁链为：

φ3=2πB1W1r12a12

(8)

三个区域总漏磁链可以表示为：

φ=φ1+φ2+φ3=2πB1W1(a1r1/3+

a12r12+a2r2/3)

(9)

根据磁路欧姆定理，磁通φ可以表示为：

(10)

(11)

式中：Hk为磁场长度，m；μ为相对磁导率，对于铁磁材料，μ=1；μ0为绝对磁导率，H/m；S为磁路面积，m2。

在Hk相对零序滤波器线圈绕组占据空间以外部分，磁力线发散，磁阻很小，所以有效的磁路长度取值为绕组的高度[7]。

结合式(10)及式(11)，磁通密度Bk为：

Bk=ρφ/S=I1W1μ0ρ/H1

(12)

式中：ρ为磁路长度修正因数；I1为流过绕组的电流，A。

将式(12)代入式(9)，则总漏磁链为：

(13)

该漏磁组的漏电抗Xk为：

(14)

式中：f为系统频率，Hz；Lk为漏电感，H。

4.2 能量算法

磁场能量用函数关系来表达，可以写为：

(15)

式中：IN为额定电流，A；B为漏磁通密度，T；H为磁场强度，A/m；v为漏磁场分布空间。

由式(15)可得漏电感为：

(16)

根据式(16)，通过在一定空间中对B、H进行体积积分，求出漏电感的方法称为磁场能量算法。文献[8]指出采用相对漏磁链法无法对横向漏磁进行准确计算，当线圈半径与高度之比较大时，采用相对漏磁链法可能会造成一定误差。而能量算法是利用滤波器漏磁场空间范围内磁场能量的平均值与电感的关系计算漏电抗，可用于复杂结构中对漏电抗的计算。

在柱坐标系下，零序滤波器的漏磁场分布可以用泊松方程边值问题描述[9]：

(17)

B、H可以在ANSYS软件中利用有限元法求解式(17)并进行旋度计算得到，对B、H积分运算后，可以求出整个空间漏磁场总能量，再代入下式求出漏电抗X的大小：

(18)

式中：Wm为轴对称模型的漏磁场总能量，J；Ik为工作电流，A。

5 仿真结果分析

在PSCAD/EMTDC软件中搭建仿真电路，谐波源采用单相二极管全波整流电路，会产生3次、5次、7次等奇次谐波。仿真系统视在功率为 10kVA，线电压为380V。

当三相电压平衡时，中性线电流滤波前后电流波形如图4、图5所示。通过对比图4和图5，加装零序滤波器后，中性线电流的峰值减小，为不加零序滤波器时的1/4，并且每相的3次谐波电流都大为减小。经计算，相电流总谐波畸变率从208.7%降低到163.2%，表明零序电流大都通过滤波器回流至负载，但由于系统及滤波器本身存在一定大小的零序阻抗，零序电流没有完全经滤波器滤除，相电流频谱中还存在3次谐波电流。

图4 滤波前中性线仿真电流

图5 滤波后中性线仿真电流

在系统三相平衡电压中，每相加入10V同相电压来模拟三相不平衡电压。由图6可以看出，即使系统中只有10V的零序电压，也会产生14倍左右的电流流经中性线。如图7所示，加装阻零器后，即使有同样的零序电压，中性线电流峰值比0.15A还小，相电流总谐波畸变率从208.7%降低到154.1%。可见，仿真结果验证了零序滤波器与阻零器结合具有很好的滤波效果。

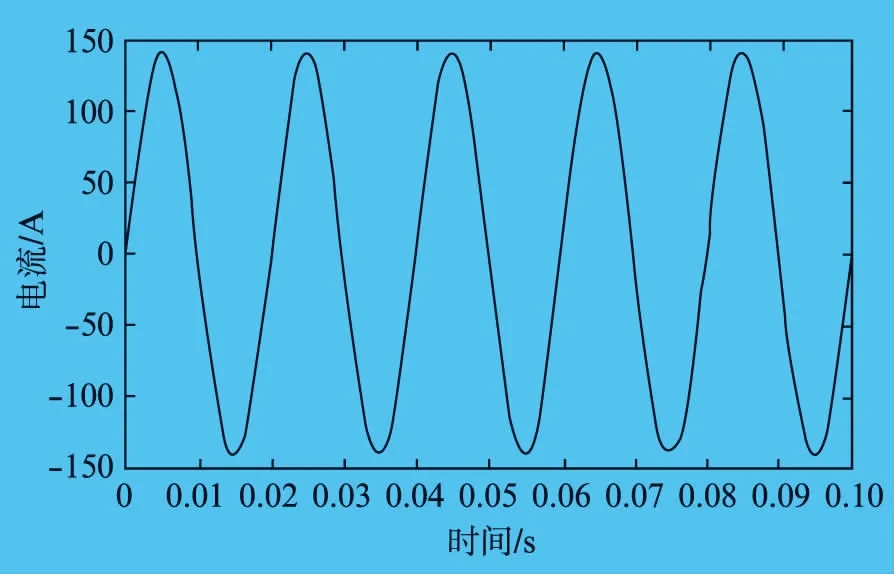
图6 电压不平衡时中性线仿真电流

图7 加装阻零器后中性线仿真电流

为了直观地描述零序滤波器漏磁场分布情况，在ANSYS软件中搭建滤波器铁芯与线圈结构的二维磁场模型[10]。以10kVA样机为例，结合图3，ANSYS模型参数中铁芯柱半径为3.5cm，h为 18cm。实际绕组采用双筒多匝并绕方式，对其中一相磁路进行简化分析，不考虑绕组之间的绝缘材料，将内外绕组作为块状导体，令a1=a2=0.4cm，hc=12cm，a12=0.8cm，r1=4.5cm。

内外绕组和空气的相对磁导率取1，铁芯相对磁导率设为3000，单元类型选择具有8节点的二维单元PLANE53，加载方式采用在内外绕组分别施加方向相反的电流，单位面电流密度相等，外边界设置磁通平行的边界条件，求解后得到如图8所示的漏磁通磁力线分布。

图8 漏磁通磁力线分布

由图8可以看出，漏磁通磁力线基本平行于对称轴分布，形成纵向漏磁，并且在两个绕组之间分布最密集。横向漏磁只在铁芯端部出现，所占比例较小。漏磁通主要路径为非铁磁性绕组及周围空气。

在通用后处理器中得到铁芯、空气及绕组中的能量，见表1。

表1 模型漏磁能量 mJ

由表1可知，漏磁能量主要集中在空气与绕组中，将总的漏磁能量代入式(18)，得到漏电抗为0.45Ω。

6 试验验证

对400V、100A零序滤波器的滤波效果进行试验验证。利用隔离变压器在实验室中建立三相四线制供电系统，采用三个带大电容滤波的单相不控整流电路来模拟负载谐波源，产生各奇次谐波电流，采用40Ω电阻作为系统负载，使用CA8335电能质量分析仪记录试验数据与波形。当系统电压为120V时，滤波前后中性线电流如图9、图10所示。由试验结果可以看到，中性线电流有效值从10.8A减小到0.2A，可见零序滤波器起到了很好的滤波作用。

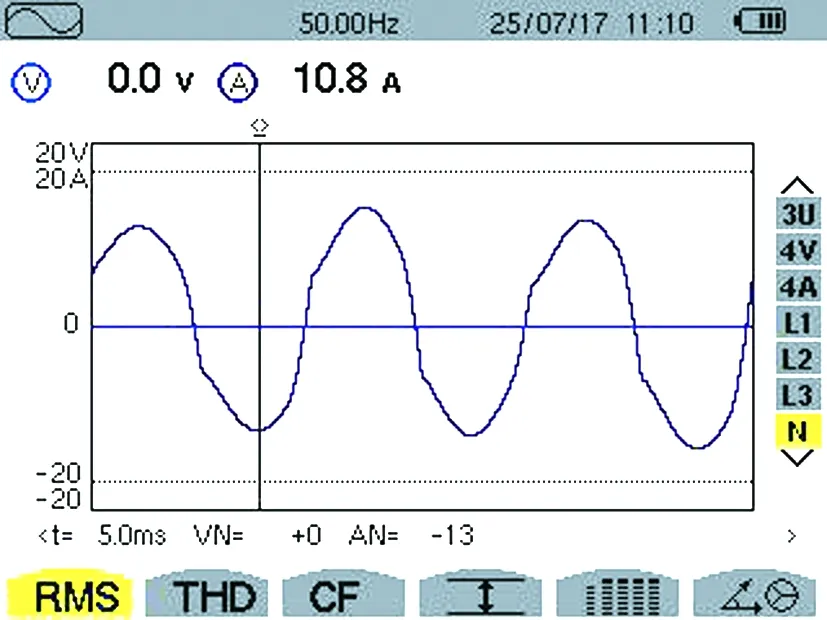
图9 滤波前中性线试验电流

图10 滤波后中性线试验电流

对滤波前后A相电流进行傅里叶分解，得到各次谐波含量，如图11、图12所示。3次谐波含量从3.5A减小到0.2A，9次谐波电流从0.4A减小到0.02A，15次谐波电流也从0.2A减小到 0.03A，可见，零序谐波电流下降明显。

图11 滤波前A相电流试验频谱图

图12 滤波后A相电流试验频谱图

零序阻抗的测量应在额定频率下进行，将零序滤波器的三个上半绕组与三个下半绕组分别短接，然后在短接后的绕组上施加单相电压进行测量。由于零序阻抗很小，为了防止过流，利用调压器将测量电压调低，并在中性线上串联一个保护电阻。在不同电压条件下测得的零序阻抗见表2。

表2 零序阻抗测量数据

对4组零序阻抗取平均值，得到阻抗大小为0.533Ω。因为导线电阻的存在，所以实际测量值稍高于仿真计算结果。

7 上网运行

为了验证该零序滤波器工业样机的现场运行情况和滤波效果，在广东茂名市北边坡箱变上网运行。图13为安装现场，图14为零序滤波器未投入运行时仪表盘上的显示数据。

图13 零序滤波器安装现场

图14 零序滤波器仪表显示

经测试，北边坡箱变线路在滤波前各相数据见表3，中性线电流为74.7A。

表3 滤波前线路数据

当零序滤波器投入电网后，中性线电流从 74.4A 减小为27.3A。滤波前后中性线电流谐波含量如图15、图16所示，可以看出3次谐波电流从10.24A减小为0.79A，大部分被滤波器滤除，滤波效果达到工程及用户要求。

图15 滤波前中性线电流谐波含量

图16 滤波后中性线电流谐波含量

8 结束语

笔者提出了一种磁通补偿型零序滤波器，这一零序滤波器结构简单，不需要复杂的控制算法，滤

波效果受系统参数影响小。为了减小因系统不平衡电压引起的零序电流，可以在电源与零序滤波器之间加装阻零器。由于零序阻抗是影响滤波效果的关键因素，因此建立了铁芯与绕组的二维模型，根据漏磁链法和磁场能量法对零序阻抗进行数值计算。通过仿真与试验验证，与阻零器结合的零序滤波器具有很好的滤波效果[11]。现场测试结果表明，零序滤波器的滤波效果满足用户对谐波电流滤除的要求，这一新型磁通补偿型零序滤波器可以起到净化电网的作用。

[1] 冯兴田，孙添添，马文忠.配电网电能质量调节装置集散配置策略[J].电力系统保护与控制，2015，43(24)： 33-39.

[2] SUBJAK J S, MCQUILKIN J S. Harmonics-Cau-ses, Effects, Measurements, and Analysis： An Up-date[J]. IEEE Transactions on Industry Applications, 1990,26(6)： 1034-1042.

[3] EMANUEL A E. On the Assessment of Harmonic Pollution [of Power Systems][J]. IEEE Transactions on Power Delivery, 1995,10(3)： 1693-1698.

[4] 王彬.基于磁通补偿原理的零序滤波器的研究[D].北京： 华北电力大学,2016.

[5] 徐绍麟.城市电网10kV低阻接地系统中接地变压器零序保护接线方案[J].继电器,2003,31(9)： 35-39.

[6] LIAO C B, RUAN J J, LIU C, et al. 3-D Coupled El-ectromagnetic-Fluid-Thermal Analysis of Oil-Immersed Triangular Wound Core Transformer[J]. IEEE Transactions on Magnetics, 2014,50(11)： 1-4.

[7] 李岩，李龙女，井永腾，等.轴向双分裂发电机变压器漏磁场及穿越短路阻抗计算与分析[J].高电压技术,2014,40(6)： 1623-1629.

[8] 潘东海.DSBC树脂浇注式变压器电场和磁场计算[D].北京： 华北电力大学,2011.

[9] 李锦彪,周重芝.变压器铁心拉板损耗的计算与分析[J].变压器,1995,32(6)： 17-20.

[10] 冯静.基于ANSYS的漏感变压器的仿真计算[D].成都： 电子科技大学,2011.

[11] 李守法，刘文博.模块化三电平有源滤波器的研制[J].上海电气技术，2017，10(1)： 21-24.