间隙泄漏对透平级气动性能影响的数值研究

陈阳, 李军, 周帅, 曹守洪, 孔祥林, 孙奇

(1.西安交通大学能源与动力工程学院, 710049, 西安; 2.东方汽轮机有限公司产品研发中心, 618000, 四川德阳)

透平机械中间隙泄漏带来的损失是其气动损失的重要组成部分[1-2]。随着透平通流精细化设计和实验、数值手段的发展,科研人员对间隙泄漏流动开展了一系列的研究。例如,Gier等通过实验与数值分析对叶顶泄漏流进行研究,总结了5类泄漏损失:泄漏工质的旁通损失、与主流的掺混损失、泄漏间隙中的鼓风损失、流动中的台阶损失以及随后附带的下游级损失,分析了这5类损失各自占总泄漏损失的比例,掺混损失大约占总损失的50%,旁通损失和台阶损失大约各占总损失的20%,附带的下游级损失占比较小而鼓风损失几乎可忽略[3];Pfau等在透平实验台上开展了叶顶迷宫密封泄漏流动与主流相互作用的研究,结果表明迷宫密封泄漏流动改变了动静气流匹配并引起了流动损失[4];Rosic等结合实验测量与数值模拟开展了叶顶间隙和动静腔室结构对透平级气动性能的研究,结果指出可以通过优化叶顶腔室结构控制泄漏流形态来提高透平级气动效率[5-6]。

孙皓等基于透平级实验数据,采用数值模拟研究了叶顶间隙泄漏对主流流场和二次流发展的影响[7];Barmpalias等实验研究了不同汽轮机叶顶间隙结构的气动性能,研究给出了最优的汽轮机叶顶间隙结构,保证了汽轮机的通流效率[8];高杰等通过数值模拟给出了叶顶间隙泄漏涡的发展形态,获得了泄漏涡与主流通道涡的作用规律[9];Palmer等基于实验和数值分析定量研究了叶顶间隙泄漏流动损失产生机理,为叶顶间隙流动损失的预测提供了分析工具[10];曹丽华等数值研究了汽轮机迷宫密封泄漏流动形态及其对汽轮机级气动性能的影响[11]。

Moroz等对隔板腔室及平衡孔结构进行了数值分析,指出平衡孔内存在着复杂的三维涡系运动,并且对主流产生影响[12]。刘网扣等采用数值分析研究了平衡孔面积变化对透平级效率和气动性能的影响,发现在平衡孔面积较小时,级效率将随着平衡孔面积的增加快速增加,但当平衡孔面积达到一定值后再持续增加时,级效率提升变缓并最终不再发生明显变化[13]。

多级轴流透平级中通常存在着多种间隙泄漏流动,间隙泄漏流动对透平气动性能影响的研究需要细化。目前已有研究主要集中在叶顶间隙泄漏流动方面,而对叶根与转轴隔板间隙以及动叶叶根与轮盘间隙泄漏流动方面的研究较少。

东方汽轮机有限公司建造了国内首台三级空气透平实验台[14],并基于该实验台已经进行了若干实验和数值研究工作[15-16]。本文在前期实验和数值模拟工作的基础上,进一步针对该三级透平开展了包括动叶叶顶间隙、静叶叶根与转轴间隙(简称隔板间隙)和动叶叶根与轮盘间隙(简称叶根间隙)的泄漏流动对透平性能影响的数值研究,旨在细化真实透平级流动细节和损失产生机制,提高实际透平机组气动设计水平。

1　计算模型和数值方法

本文基于所考虑的泄漏区域不同,分别设计了包含不同计算域的4种计算模型。各模型所包含的计算域范围说明详见表1。表1中各模型所考虑的计算域范围逐次增大,而模型4则考虑了三级透平的完整泄漏结构,该模型相应的全结构数值计算域如图1所示。第1级静叶和第1级动叶分别用S1和R1表示,第2和第3级静动叶采用类似方法表示。表1中模型4和模型3的叶根间隙建模方法如图2所示。模型4中完整的叶根间隙共包含3组动叶斜齿枞树型叶根间隙结构,每组枞树型斜齿与轮盘间隙共有11段小间隙,而模型3则忽略了其中的8段几何尺寸较小的小间隙。

表1　4种模型计算域范围说明

三级透平静动叶的主要几何参数见表2,其中间隙的相对高度定义为汽封齿处间隙高度与对应叶片叶高的比值。

图1所示所有计算域均借用文献[15]中的多块结构化计算网格,整个计算区域的总网格数约4 162万,其余模型网格在该网格基础上依次删减。所有数值求解均采用MUMECA-FINE求解器进行稳态求解,并以理想空气为计算工质,更具体的数值方法参见文献[15]。4种模型在同一转速下进行计算,

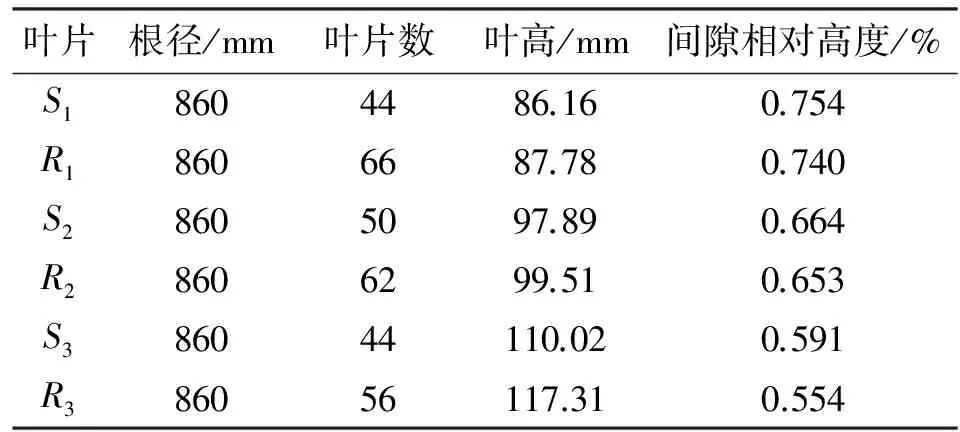
表2　三级透平叶片主要几何参数

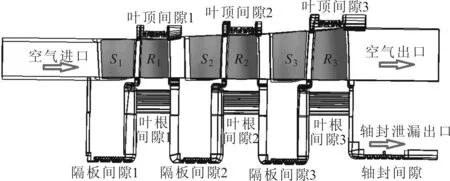
图1　三级透平全结构数值计算域

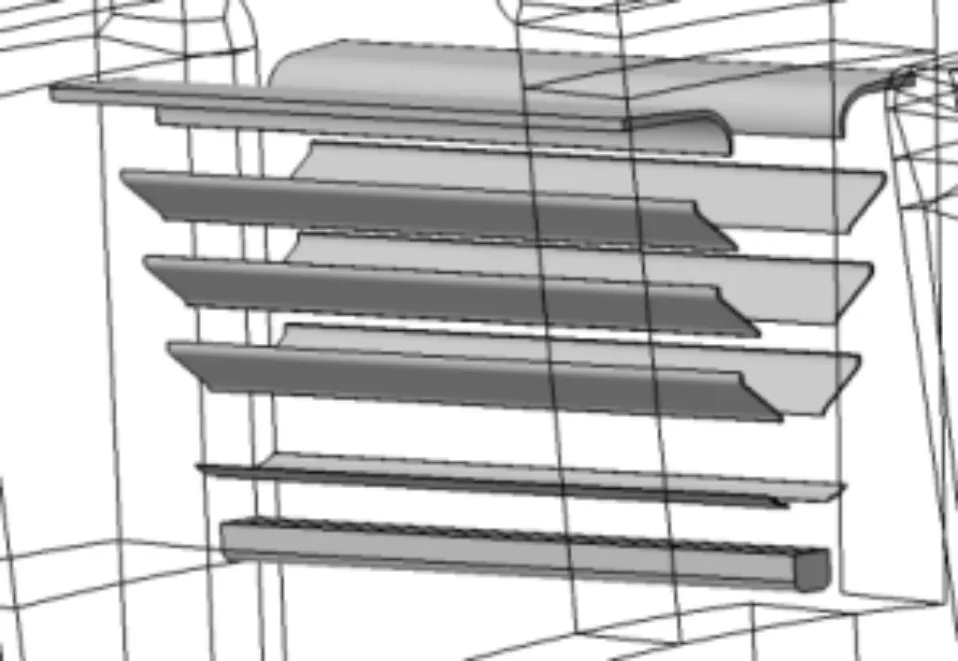
(a)叶根间隙几何模型

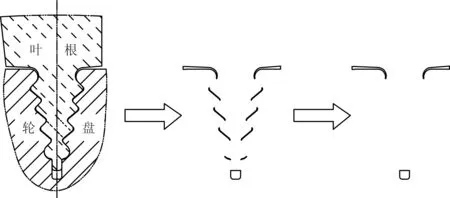
(b)叶根间隙剖面结构图2　叶根间隙建模示意

进口边界给定总压及总温,出口边界给出平均静压。进出口具体的边界条件数值依据实验测量值确定。

文献[15]给出了该实验透平在不同转速下基于模型4计算得到的数值结果与相应转速下实验数据的对比,两类数据曲线吻合良好,验证了数值方法的可靠性。图3是数值计算得到的考虑和不考虑枞树型叶根间隙时第2级反动度沿叶高的分布(图中相对叶高按动叶实际叶高进行归一化处理,反动度仅给出了相对值)。从计算结果来看,模型2在根部区域反动度要稍高于模型4,而在顶部区域两模型反动度基本相同。文献[16]实验研究了透平级在封堵和不封堵枞树型叶根间隙时根顶部反动度随速比的变化情况,指出封堵枞树型叶根间隙后(相当于模型2),透平级根部反动度增加,顶部反动度在间隙封堵前后变化不大。可以看出本文数值计算的反动度变化趋势和文献[16]中实验结果一致,进一步验证了本文数值方法的可靠性。

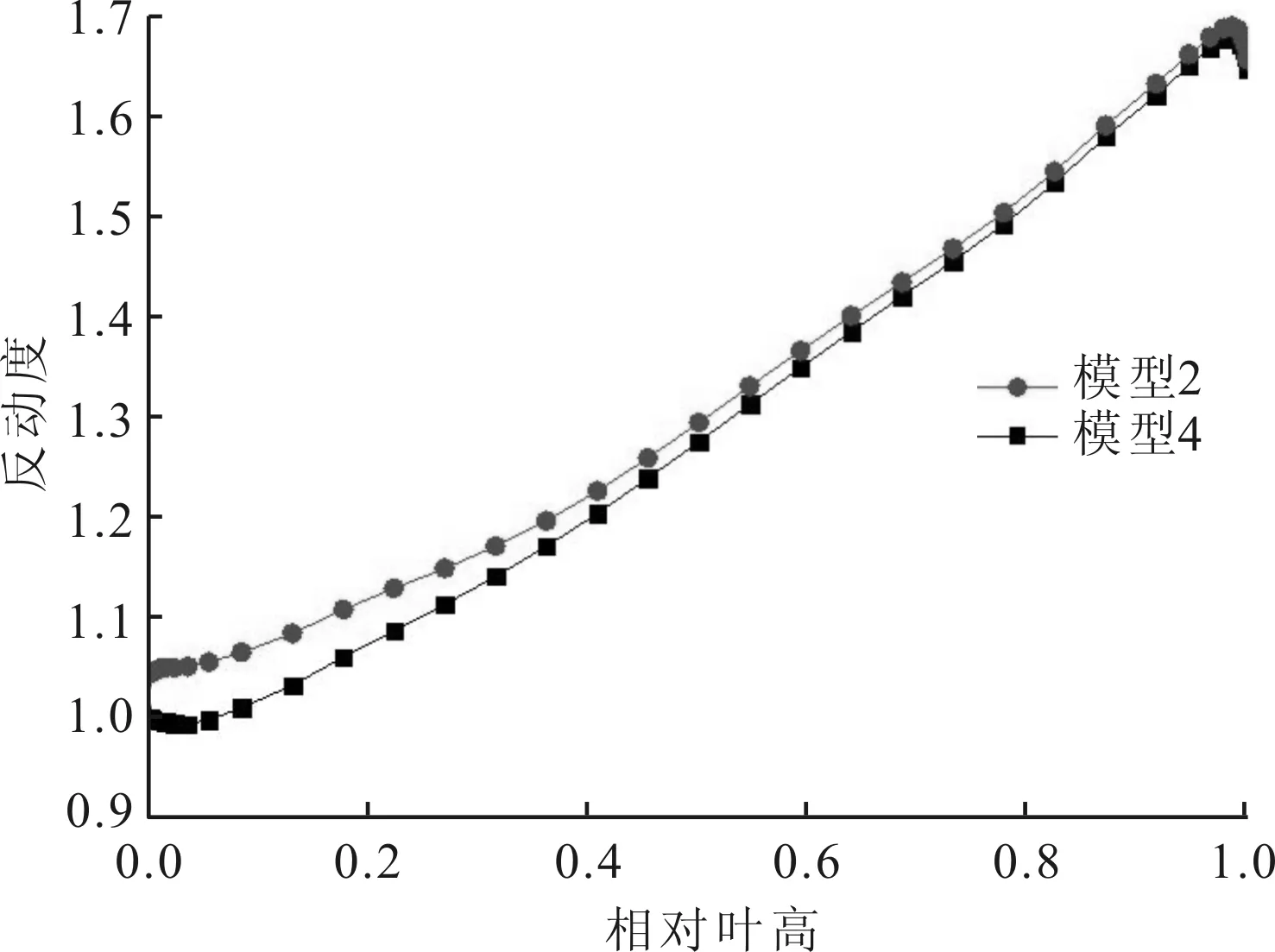
图3　第2级反动度沿叶高的分布

2　结果分析与讨论

2.1　气动性能对比

图4比较了4种计算模型的透平效率,图4中所有效率以模型1的效率为基准给出相对数值。一般情况下,透平效率随间隙泄漏的增加而降低,但在图4中,计算得到的透平效率并没有随所考虑间隙泄漏的增加而持续下降。

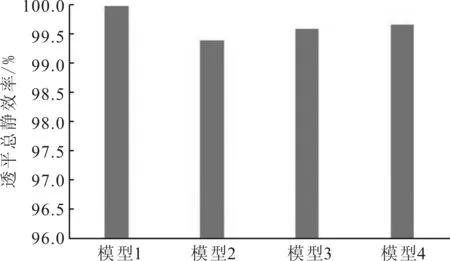
图4　4种计算模型的透平总静效率比较

与模型1相比,虽然当考虑叶顶间隙和隔板间隙泄漏时,模型2的总静效率下降了0.62%,但是当进一步考虑部分枞树型叶根间隙泄漏影响时,模型3总静效率却仅减小了0.41%,当考虑全部叶根间隙泄漏时,模型4总静效率仅减小了0.34%。可见,叶顶间隙和隔板间隙泄漏的存在带来透平效率的下降,但同时枞树型叶根间隙的存在却又在一定程度上具有提升透平效率的作用。

2.2　流场特性分析

图5给出了模型2和模型4的间隙泄漏情况。图5中箭头表示泄漏流的流动方向,数字表示泄漏流流量的大小。由于模型1为纯通流,流场结构较为简单,模型3和模型4几何差异较小,因此本文采用模型2和模型4进行流场分析。

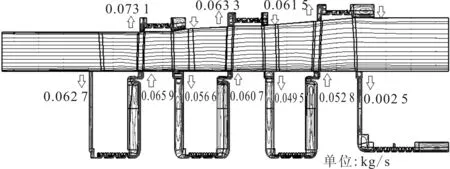
(a)模型2

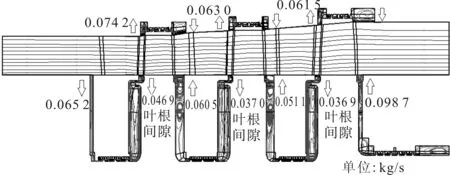
(b)模型4图5　模型2和模型4的间隙泄漏图

由图5可知,叶顶间隙泄漏不受枞树叶根间隙的影响,无论是否考虑枞树型叶根间隙,叶顶的泄漏流流量和方向总体上保持不变。然而,隔板泄漏流却受到枞树型叶根间隙的影响。

对于主流与泄漏流的交互作用,本文定义泄漏流流入主流为“吸”,主流部分流体流出主流通道为“漏”。对于完全不考虑枞树型叶根间隙的模型2,靠近叶根端区的主流由级前漏入隔板间隙,并在隔板间隙狭小空间内耗散为低能流体,然后这些低能流体又全部被吸入动静叶级间成为主流的一部分。

与模型2相比,模型4的隔板间隙的泄漏流量和流动方向都发生了较大变化。一方面,从主流漏入隔板的流体流量总体上都有所下降,另一方面,泄漏流在同级隔板左右两侧与主流的交互方向发生了改变。气流由级间漏入隔板右侧间隙,与同级隔板左侧来的泄漏流掺混,掺混后通过叶根间隙流入下一级隔板左侧。对于叶根间隙的流动,文献[15]给出了动叶轮盘两侧隔板间隙泄漏流动的局部放大图。文中清晰地显示了泄漏流从上游经过叶根间隙流向下游时隔板间隙内的流动形态。

隔板泄漏流之所以能够通过叶根间隙流入下一级隔板间隙,主要是因为透平隔板间隙通道中的静压低于上一级隔板通道中的静压,而叶根间隙的存在恰好连通了上下级隔板间隙通道,从而使得上一级隔板右侧通道内的气流在压差作用下直接通过叶根间隙流入下一级隔板左侧通道,这又在一定程度上影响了隔板通道内静压分布,引起隔板泄漏流与主流之间的“吸”与“漏”。

当不存在枞树型叶根间隙时,隔板间隙泄漏只能在透平级静动叶级间的位置被“吸”入主流,动叶根部前缘端区流量瞬间增大引起该局部区域压力升高,最终使得级根部区域反动度升高,这是导致模型2根部反动度高于模型4根部反动度的原因。

图6和图7分别给出了第2级静叶和动叶的能量损失系数沿叶高的分布。能量损失系数由下式计算

(2)

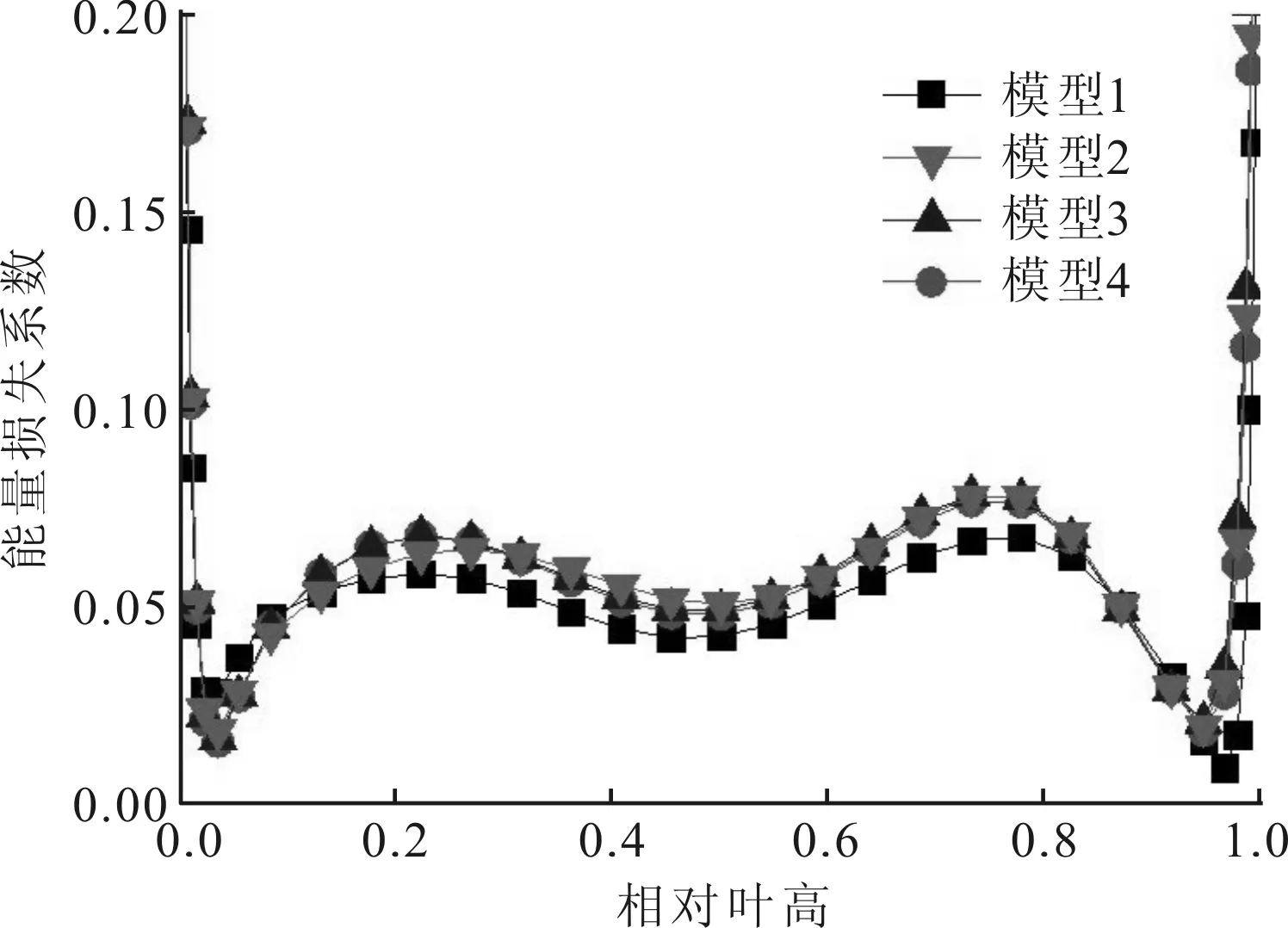
(a)叶高区域

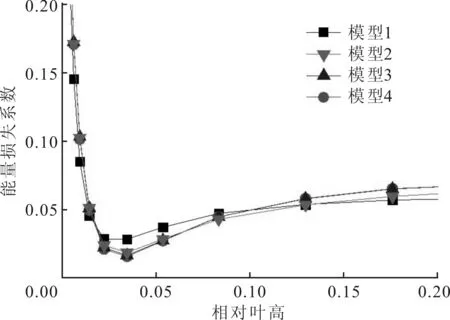
(b)近叶根区域

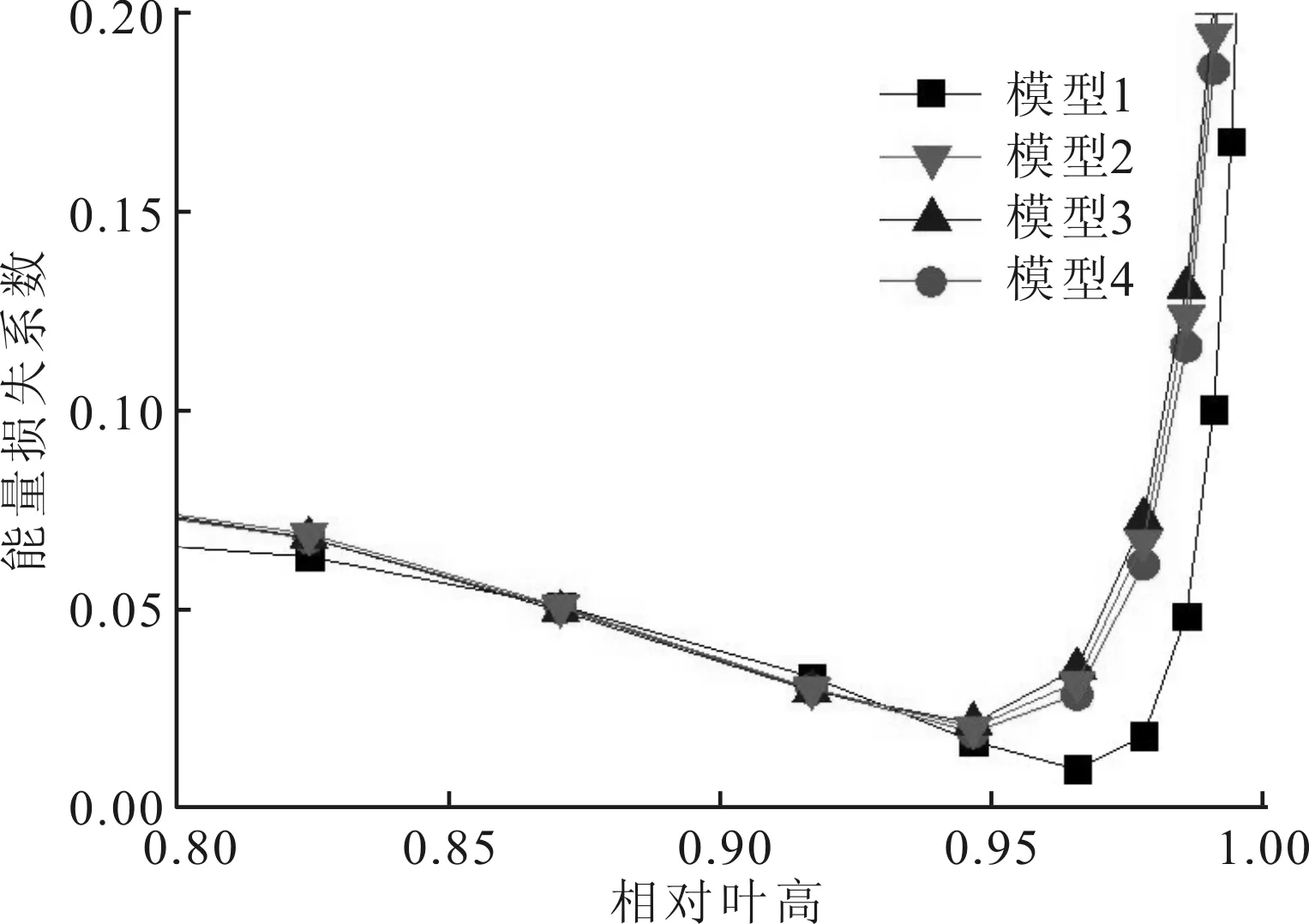
(c)近叶顶区域图6　第2级静叶能量损失系数沿叶高的分布

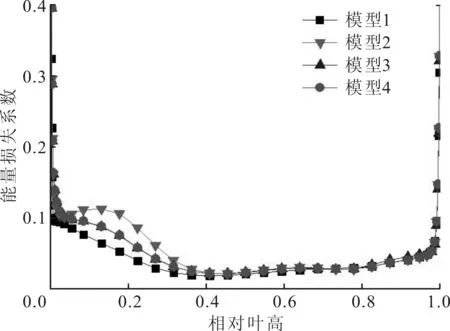
(a)叶高区域

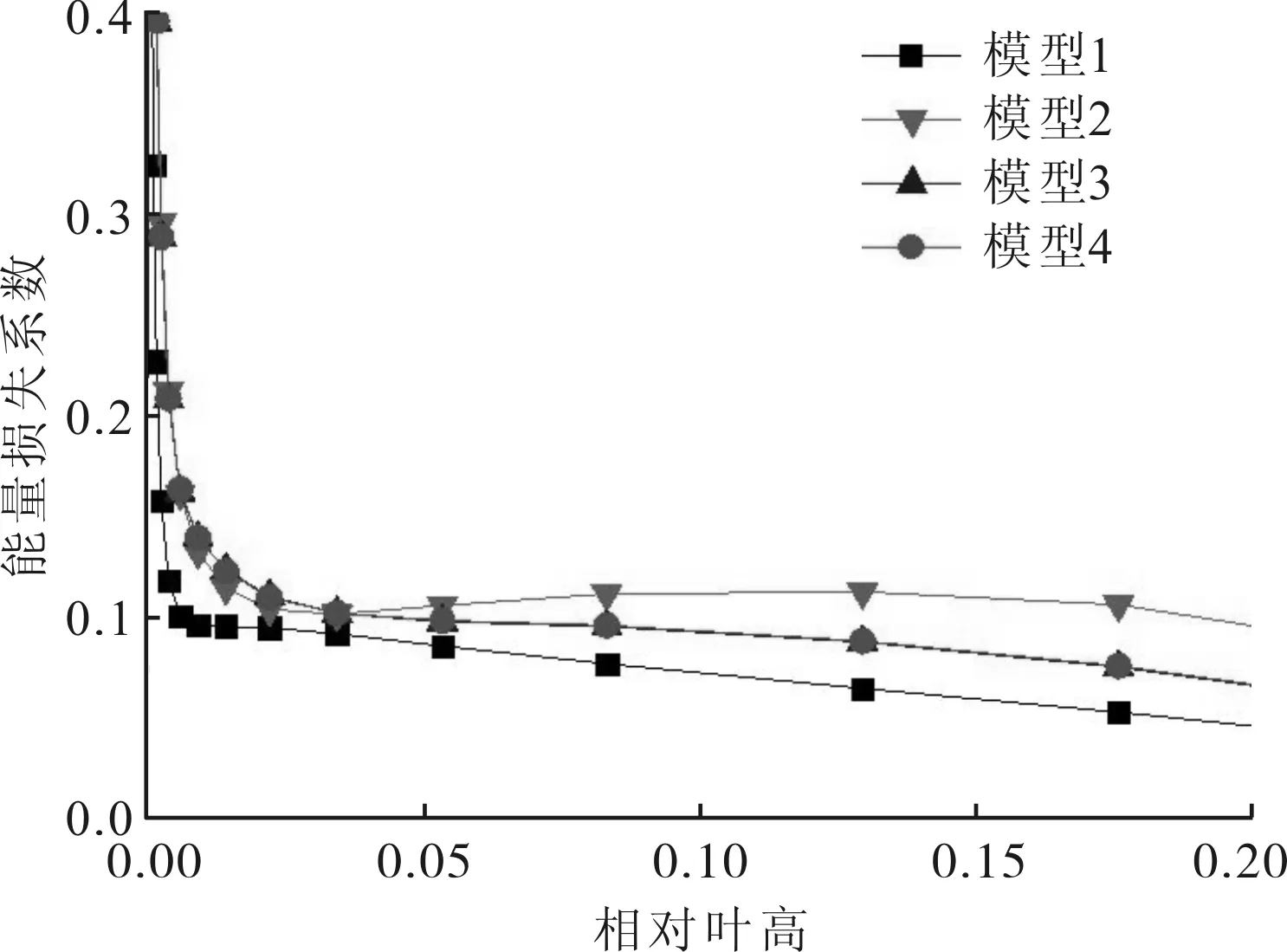
(b)近叶根区域

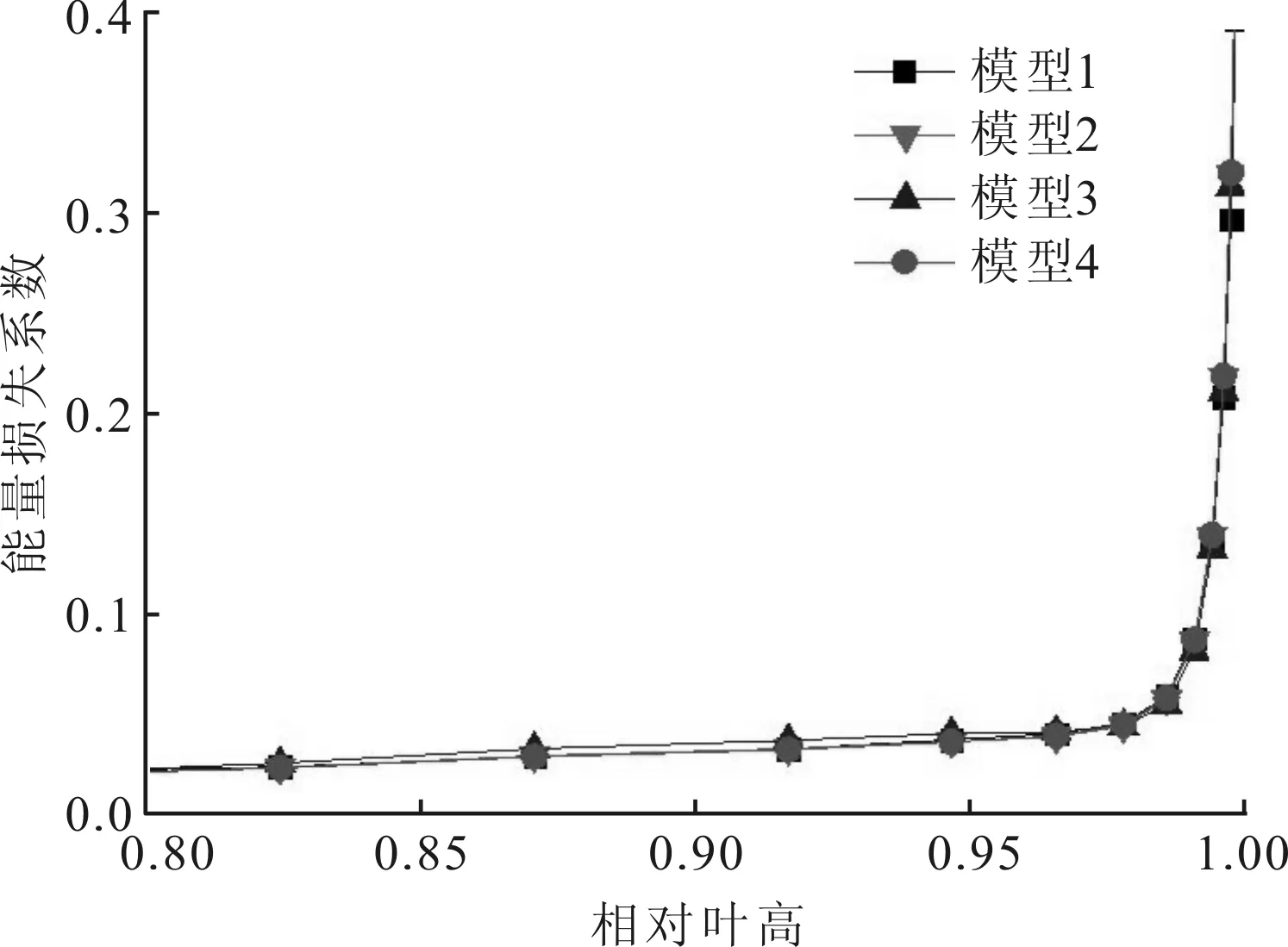
(c)近叶顶区域图7　第2级动叶能量损失系数沿叶高分布

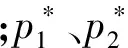
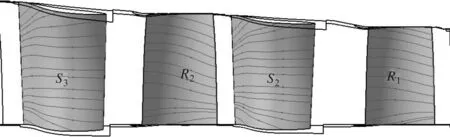
(a)模型1极限流线

(b)模型2极限流线

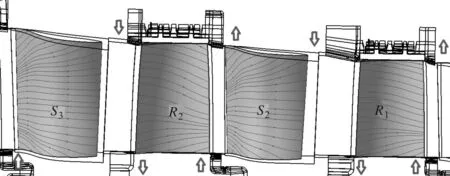
(c)模型4极限流线图8　透平级叶片表面极限流线

图8给出了模型1、模型2和模型4中间4支叶片的静叶吸力面和动叶压力面的极限流线分布,箭头方向表示叶片端区附近主流与泄漏流相互作用的方向。相对于不吸不漏的模型1、模型2和模型4中主流从第二级静动叶之间的顶部区域“漏”出,该区域附近上游S2吸力面侧二次流明显增强,而下游R2压力面侧二次流略有减弱。在根部区域,模型2泄漏流被“吸”入主流,此时,上游S2和下游R2在该区域附近的二次流均有不同程度增加;模型4中,主流由第二级级间根部“漏”出主流,上游S2吸力面侧二次流增强,而下游R2压力面侧二次流略有减弱。

通过研究图8泄漏流的方向与叶片二次流大小分布可以知道,主流与泄漏流之间的“吸”与“漏”影响叶片端区附近的二次流大小:当端区附近发生“漏”时,上游相邻叶片相应部位二次流增强,而下游相邻叶片相应部位二次流减弱;反之当端区附近泄漏被“吸”入主流时,上下游相邻叶片对应位置二次流均有不同程度增强。

按照上述“吸”和“漏”对二次流大小影响的关系原则,表3给出了第二级静动叶根部端区附近模型2和模型4二次流变化趋势的预测(与模型1相比),预测结果和图8中第二级静动叶根部端区二次流分布完全一致。同时,文献[15]的研究也指出,考虑全部间隙时(相当于本文模型4),第二级静叶前缘和第二级动叶尾缘附近横截面上二次流均有增强,表3的预测与该结论也完全一致。

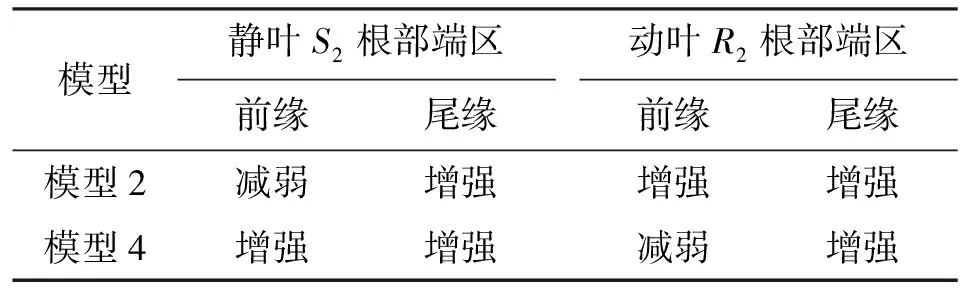
表3　第二级静动叶根部端区二次流趋势预测表

由于模型4中静叶S2根部端区前后缘二次流均增强,所以模型4中静叶S2根部端区能量损失系数略大于模型2;类似地,模型2中动叶R2根部端区能量损失系数又略大于模型4。

枞树型叶根影响隔板泄漏流与主流之间的“吸”与“漏”,且在最终效果上又能在一定程度上对透平效率起到提升作用,这种现象与平衡孔所引发的现象有类似之处。可见,合理设计枞树型叶根(或平衡孔)等结构,通过恰当地控制好级内泄漏流与主流的“吸”与“漏”来引导透平级内二次流的重新分布与发展,对提高透平气动性能具有积极的作用,这种方法对于展弦比较小的透平级将会更为有效。

3　结　论

基于三级实验透平的4种不同计算模型,采用数值模拟的方法研究了间隙泄漏流动对透平级气动性能和流场特性的影响,得到如下结论:

(1)与没有考虑泄漏流的三级纯通流透平相比,考虑所有泄漏流的三级透平总静效率降低了0.34%,其中动叶叶顶间隙和隔板间隙泄漏流使得透平总静效率降低了0.62%,但枞树型叶根与轮盘间隙泄漏使得透平总静效率提高了0.28%(约为动叶叶顶和隔板间隙泄漏引起的效率总下降幅度的45%)。适当的枞树型叶根间隙泄漏对透平效率具有一定提升作用。

(2)枞树型叶根间隙泄漏流改变了叶根端区附近隔板泄漏流与主流的相互作用方向及泄漏流的大小,进而改变了叶根端区附近反动度和能量损失系数。

(3)叶片端区泄漏流影响透平叶片端区能量损失系数的分布;隔板间隙泄漏对动叶根部区域能量损失系数有较明显影响。从整个叶高范围来看,泄漏流总体上对静叶能量损失系数的影响大于对动叶能量损失系数的影响。

(4)主流与泄漏流之间的“吸”与“漏”影响叶片端区附近二次流的分布与发展,并最终带来透平气动性能的变化。当端区附近发生“漏”时,上游相邻叶片端区二次流增强,而下游相邻叶片端区二次流减弱;反之当端区附近泄漏被“吸”入主流时,上下游相邻叶片对应位置二次流均有不同程度增强。

参考文献:

[1]DENTON J D. Loss mechanisms in turbomachines [J]. ASME Journal of Turbomachinery, 1993, 115(4): 621-656.

[2]COFER J I I V. Advances in steam path technology [J]. ASME Journal of Engineering for Gas Turbines and Power, 1996, 118(4): 337-352.

[3]GIER J, STUBERT B, BROUILLET B, et al. Interaction of shroud leakage flow and main flow in a three-stage LP turbine [J]. ASME Journal of Turbomachinery, 2005, 127: 649-658.

[4]PFAU A, KALFAS A I, ABHARI R S. Making use of labyrinth interaction flow [J]. ASME Journal of Turbomachinery, 2007, 129(1): 164-174.

[5]ROSIC B, DENTON J D, CURTIS E M. The influence of shroud and cavity geometry on turbine performance: an experimental and computational study: part IShroud geometry [J]. ASME Journal of Turbomachinery, 2008, 130(4): 041001.

[6]ROSIC B, DENTON J D, CURTIS E M, et al. The influence of shroud and cavity geometry on turbine performance: an experimental and computational study: part IIExit cavity geometry [J]. ASME Journal of Turbomachinery, 2008, 130(4): 041002.

[7]孙皓, 薛志恒, 李军, 等. 低雷诺数对透平叶片间隙泄漏流动影响的研究 [J]. 西安交通大学学报, 2010, 44(3): 11-15.

SUN Hao, XUE Zhiheng, LI Jun, et al. Effects of low Reynolds number on turbine blade tip leakage flow [J]. Journal of Xi’an Jiaotong University, 2010, 44(3): 11-15.

[8]BARMPALIAS G K, ABHARI S R, KALFAS I A, et al. Design considerations for axial steam turbine rotor inlet cavity volume and length scale [J]. ASME Journal of Turbomachinery, 2012, 134(5): 051031.

[9]高杰, 郑群, 许天帮, 等. 涡轮间隙泄漏涡破碎对损失的影响 [J]. 航空学报, 2014, 35(5): 1257-1264.

GAO Jie, ZHENG Qun, XU Tianbang, et al. Effect of tip leakage vortex breakdown on loss in turbine [J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(5): 1257-1264.

[10] PALMER T R, TAN C S, ZUNIGA H, et al. Quantifying loss mechanisms in turbine tip shroud cavity flows [J]. ASME Journal of Turbomachinery, 2016, 138(9): 091006.

[11] 曹丽华, 贾彦铭, 李盼, 等. 汽轮机高低齿叶顶汽封泄漏流动的数值分析 [J]. 浙江大学学报(工学版), 2016, 50(8): 1545-1550.

CAO Lihua, JIA Yanming, LI Pan, et al. Numerical analysis on leakage flow of blade tip stepped seal in steam turbine [J]. Journal of Zhejiang University (Engineering Science), 2016, 50(8): 1545-1550.

[12] MOROZ L, TARASOV A. Flow phenomenon in steam turbine disk-stator cavities channeled by balance holes [C]∥Proceedings of the ASME Turbo Expo 2004 Power for Land, Sea, and Air. New York, USA: ASME, 2004: GT2004-54228.

[13] 刘网扣, 张兆鹤, 崔琦, 等. 冲动式汽轮机级平衡孔面积对级性能影响的研究 [J]. 动力工程学报, 2011, 31(8): 575-578.

LIU Wangkou, ZHANG Zhaohe, CUI Qi, et al. Influence of balance hole area on performance of an impulse turbine stage [J]. Journal of Chinese Society of Power Engineering, 2011, 31(8): 575-578.

[14] SUN Qi, KONG Xianglin, JIANG Shengke, et al. Study of multi-stage test turbine and numerical calculation [C]∥Proceedings of the ASME 2011 Power Conference Co-located with International Conference on Power Engineering. New York, USA: ASME: 55399.

[15] CHEN Yang, LI Jun, TIAN Chaoyang, et al. Experimental and numerical investigations on the aerodynamic performance of the three-stage turbine with consideration of the leakage flow effect [C]∥Proceedings of the 2016 ASME Turbo Expo on Turbomachinery Technical Conference and Exposition. New York, USA: ASME: GT2016-56407.

[16] 冯增国, 田朝阳. 枞树型叶根间隙漏气对级性能影响的试验研究 [J]. 东方汽轮机, 2016(2): 11-13.

FENG Zengguo, TIAN Chaoyang. Experimental study on effects of leakage to stage performance in gap of fir tree blade root [J]. Dongfang Turbine, 2016(2): 11-13.

[本刊相关文献链接]

孙皖,牛璐,步珊珊,等.低温透平膨胀机内非平衡自发凝结两相流动的数值研究.2018,52(2):125-129.[doi:10.7652/xjtuxb201802019]

白治宁,周景军,蔡卫军,等.火箭助飞鱼雷分离舱张开特性试验与数值研究.2018,52(1):136-142.[doi:10.7652/xjtuxb201801020]

刘小民,魏铭,杨罗娜,等.内凹式蜗舌对多翼离心风机气动性能和噪声的影响.2017,51(12):128-135.[doi:10.7652/xjtuxb201712019]

王杰枫,范小军,李森,等.弯曲通道中凸、凹表面水膜流动特性的数值研究.2017,51(11):22-28.[doi:10.7652/xjtuxb 201711004]

蔡柳溪,高松,肖俊峰,等.壁面粗糙度对轴流压气机气动性能的影响.2017,51(11):36-42.[doi:10.7652/xjtuxb201711 006]

高庆,廖高良,张永海,等.透平级气动及运行参数对轮缘密封封严性能影响的数值研究.2017,51(7):62-72.[doi:10.7652/xjtuxb201707010]

王晟旻,琚亚平,张楚华.离心压缩机级通流与盘盖侧泄漏流的耦合分析.2017,51(7):73-77.[doi:10.7652/xjtuxb 201707011]

付曦,张俊红,寇海军,等.复杂载荷下轴流压气机叶片疲劳损伤数值研究.2017,51(5):149-155.[doi:10.7652/xjtuxb 201705021]

李丹宇,刘小民,李典.仿生翼几何特征与气动性能的关系初探.2017,51(1):88-96.[doi:10.7652/xjtuxb201701014]

范小军,李亮,李森,等.平板和静叶表面气流-水膜耦合流动特性的数值研究.2016,50(11):7-13.[doi:10.7652/xjtuxb 201611002]

李典,刘小民,杨罗娜.仿鸮翼的三维仿生翼型叶片气动特性研究.2016,50(9):111-118.[doi:10.7652/xjtuxb201609018]

陈秀秀,晏鑫,李军.蜂窝叶顶密封对透平级气动性能的影响研究.2016,50(4):14-20.[doi:10.7652/xjtuxb201604003]

杜昆,李军.跨声速涡轮叶顶间隙流动传热特性的数值研究.2016,50(4):147-152.[doi:10.7652/xjtuxb201604022]

李亮,薛太旭,李森.考虑气动和湿汽损失综合影响的低压多级透平优化.2016,50(3):22-28.[doi:10.7652/xjtuxb201603 004]

赵会晶,王志恒,唐永洪,等.叶片前缘倾掠对离心叶轮气动性能的影响.2015,49(11):1-7.[doi:10.7652/xjtuxb201511 001]

祝培源,郭振东,陈红梅,等.排汽缸全局气动优化及设计知识挖掘方法.2015,49(11):26-32.[doi:10.7652/xjtuxb2015 11005]

孙晔晨,田玉宝,席光,等.三元叶片型面造型对离心压缩机叶轮气动性能影响的数值研究.2015,49(11):135-141.[doi:10.7652/xjtuxb201511022]

霍文浩,李军,钟刚云,等.冷却结构对中压透平级蒸汽冷却性能的影响.2015,49(5):36-42.[doi:10.7652/xjtuxb201505 006]

王世柱,李志刚,李军,等.补汽对透平级气动性能和静叶汽封转子动力特性影响的数值模拟.2015,49(5):56-61.[doi:10.7652/xjtuxb201505009]

高庆,李军.间隙结构对轮缘密封封严性能及透平级气动性能影响的数值研究.2015,49(3):25-31.[doi:10.7652/xjtuxb201503005]

雷鹏飞,张家忠,贾艳俊.结构参数对局部弹性翼型气动性能的影响规律.2014,48(6):110-116.[doi:10.7652/xjtuxb2014 06019]