面向裂纹扩展的连结型刚体-弹簧离散元模型

蒋逸飞, 张俊, 何勇, 刘哲超, 赵万华

(西安交通大学机械制造系统工程国家重点实验室, 710049, 西安)

材料的裂纹扩展是一个典型的复杂非线性问题,对航空航天、机械和兵器工程等领域的发展有着重要的影响。利用数值计算方法研究材料的裂纹扩展是学者们近年来的研究热点[1-2]。目前众多基于连续介质理论建立的数值模拟方法一般都需要采用预先设置断裂面[3-4]、删除单元[5-6]、重新划分网格[7-8]或添加特殊的黏聚力单元[9-10]等复杂手段来仿真裂纹扩展,而离散元方法(DEM)不受连续介质假设的约束,能够简单、有效地跟踪材料破坏的全过程[11]。

刚体-弹簧模型是离散元方法中最常用的一种,根据单元间的作用形式,该模型分为接触型和连结型两种。接触型模型的单元间的力学参数由人为设定,通过具有相互作用的单元集合体来表达材料的宏观力学性能,这些接触参数需要借助于实验进行反复校核,建模效率较低[12-13]。连结型离散元法的相关参数由材料的力学属性直接推导得出,不需要经过实验校核[14-15]。Tavarez等基于弹性理论推导得出了连结型刚体-弹簧模型的弹簧刚度,对混凝土梁受冲击侵彻的破坏过程进行了研究[16]。Wang等定义的弹簧刚度遵循L-J对势函数的形式,模拟了含裂纹的平板在动态拉伸下的断裂过程[17]。以上研究虽然能够定性地得到材料断裂后的结果,但是由于单元排布型式对仿真结果的影响,不能准确模拟裂纹的起裂和扩展过程从而揭示材料的断裂机理。

Silling等提出基于近场动力学方法增加邻近单元作用力数可以有效地模拟裂纹扩展过程[18]。Chen等基于非局部弹簧格构方法建立了多层邻居单元的作用力模型,对材料的裂纹扩展轨迹进行了研究[19]。上述近场动力学方法和非局部弹簧格构方法虽然与离散元方法不完全相同,但是它们计算单元间作用力的思路类似,对于研究刚体-弹簧离散元模型具有一定的借鉴意义。本文基于刚体-弹簧离散元模型,提出一种多层邻近单元受力的离散元计算方法,推导了2层和3层邻近单元受力时的弹簧刚度值和断裂判据;通过计算材料在冲击作用下的裂纹动态扩展过程,分析了多层邻近单元在研究材料断裂问题时的优势。

1　材料的离散元描述

1.1　离散单元排布与多层邻近单元的关系

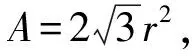
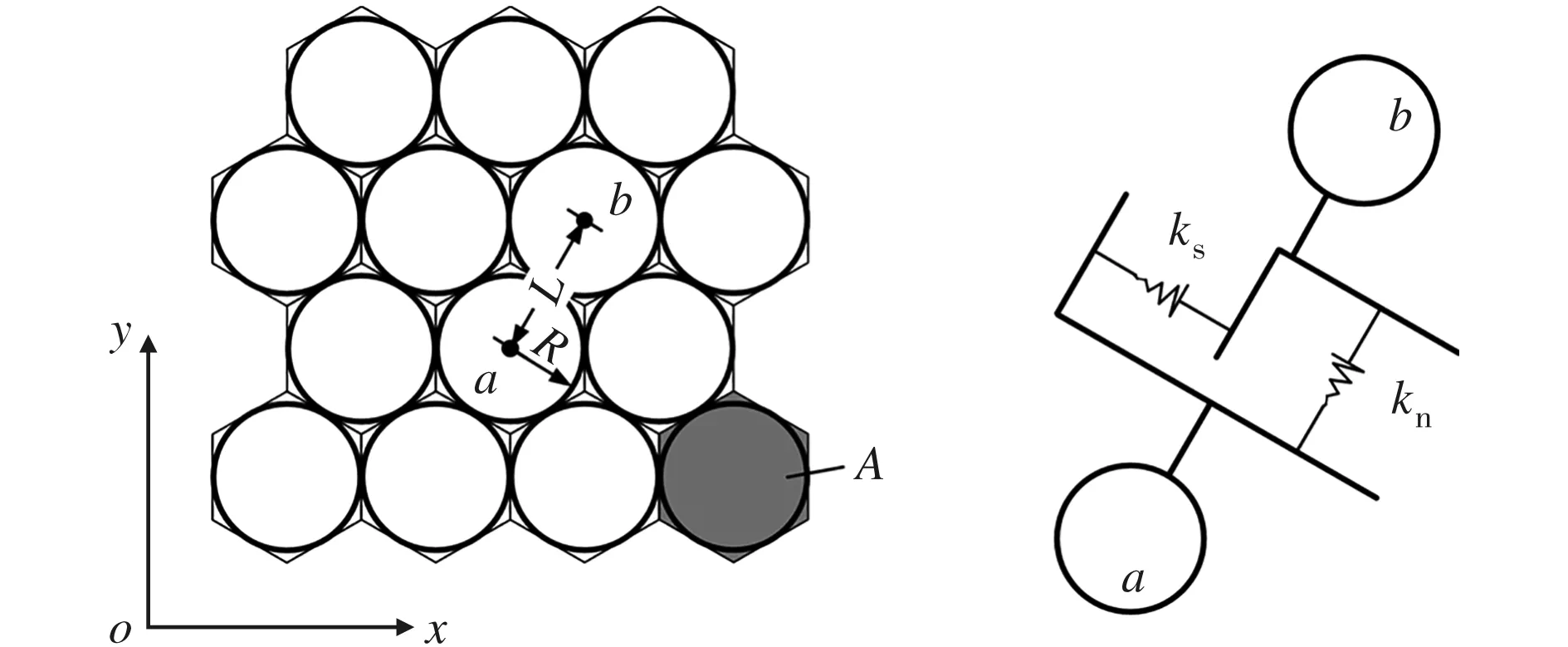
(a)离散单元二维六角点阵排布　　(b)连接元件图1　平面弹塑性材料的离散单元表达

定义εab和γab分别为单元a和b之间弹簧的正应变和切应变

(1)

式中:una、unb、usa和usb分别为单元a和单元b间的法向相对位移和切向相对位移。弹簧的应变和笛卡尔坐标系下的应变分量有如下关系

(2)

式中:l和m分别为单元a、b中心连线与x轴正方向夹角的余弦和正弦值。

定义六角点阵排布下单元的前3层邻近单元分布位置如图2所示。令单元a的邻近单元编号依次为1～18,以单元a中心为原点,x轴过第2、5、14和17号单元中心建立坐标系。前3层邻近单元与中心单元之间的平衡位置矢量用Rn(n=1,2,…,18)表示,i、j表示坐标轴单位向量,其中第1层邻近单元

(3)

第2层邻近单元

(4)

第3层邻近单元

(5)

图2　多层相邻单元分布示意图

1.2　弹簧的刚度计算

当离散单元的排布和邻近关系确定以后,材料的力学行为由弹簧的受力和变形来表达。弹簧的刚度可以通过单位体积内材料与离散单元的能量等效关系推导得出

Uc=Uk

(6)

式中:Uc为材料的变形能密度;Uk为离散单元的等效变形能密度。

根据弹性理论,平面应力时Uc可由下式表达

(7)

式中:E为弹性模量;μ为泊松比;εx、εy和γxy分别为材料在笛卡尔坐标系下的x、y方向正应变和切应变。

Uk由中心单元与邻近单元之间的弹簧变形能组成。中心单元的受力由与周围邻近单元相连的弹簧提供,因此在计算单元受力前需要确定周围邻近单元的层数或个数。在六角点阵排布条件下,单元a有q个邻近单元,当只搜索第1层邻近单元时,q=6,搜索前2层邻近单元时,q=12,搜索前3层邻近单元时,q=18。Uk可表示为

(8)

联立式(1)、(2)、(6)～(8),可以得到考虑不同邻近单元层数作用的法向和切向弹簧刚度kng和ksg(g=1,2,3)。当考虑第1层邻近单元作用时

(9)

当考虑前2层邻近单元作用时

(10)

当考虑前3层邻近单元作用时

(11)

1.3　弹簧的失效判据

选用最大拉应力准则作为材料的断裂判据,当材料受力超过抗拉强度σult时,材料发生破坏。该断裂判据在刚体-弹簧模型中用弹簧失效来描述。规定当2个单元间法向和切向合力的绝对值达到临界值fcr时弹簧失效,材料在该弹簧所在位置处发生破坏。fcr为弹簧法向和切向合力的临界值

(12)

式中:fncr和fscr分别为法向和切向弹簧的临界值,由材料的拉伸强度推导得出[16]

(13)

将弹簧刚度值代入式(13),可以得到考虑不同相邻层数作用时弹簧的失效临界值fncrg和fscrg(g=1,2,3)。当考虑第1层邻近单元作用时

(14)

当考虑前2层邻近单元作用时

(15)

当考虑前3层邻近单元作用时

(16)

2　裂纹动态扩展算例

在裂纹动态扩展的研究领域,Kalthoff和Winkler[20]的动态剪切实验非常经典,如图3所示。本文利用该实验得到的裂纹扩展路径对多层邻近单元离散元仿真结果进行验证。实验布置如图3a所示,受冲击剪切的平板尺寸为200 mm×100 mm×9 mm,平板左端有两条沿水平轴平行对称分布的切槽,裂纹长度为50 mm。子弹宽度与两切槽间距同为50 mm,子弹以16.5 m/s的速度沿x轴正方向冲击两切槽间的平板材料。平板材料为马氏体不锈钢18Ni1900,其弹性模量E=190 GPa,密度ρ=8 000 kg/m3,泊松比μ=0.3,抗拉强度σult=2 020 MPa,Rayleigh波速cR=2 799 m/s。实验中的平板和冲击加载形式均沿x轴线对称,在冲击过程中位于上下两切槽端部萌生的裂纹及其扩展轨迹也相互对称。实验发现,当冲击速度小于30 m/s时平板上半部分的裂纹将会在切槽端部萌生并沿与x轴正向夹角约70°的方向扩展。图3b所示为实验中冲击速度为16.5 m/s时,平板上半部分的裂纹扩展路径[20]。

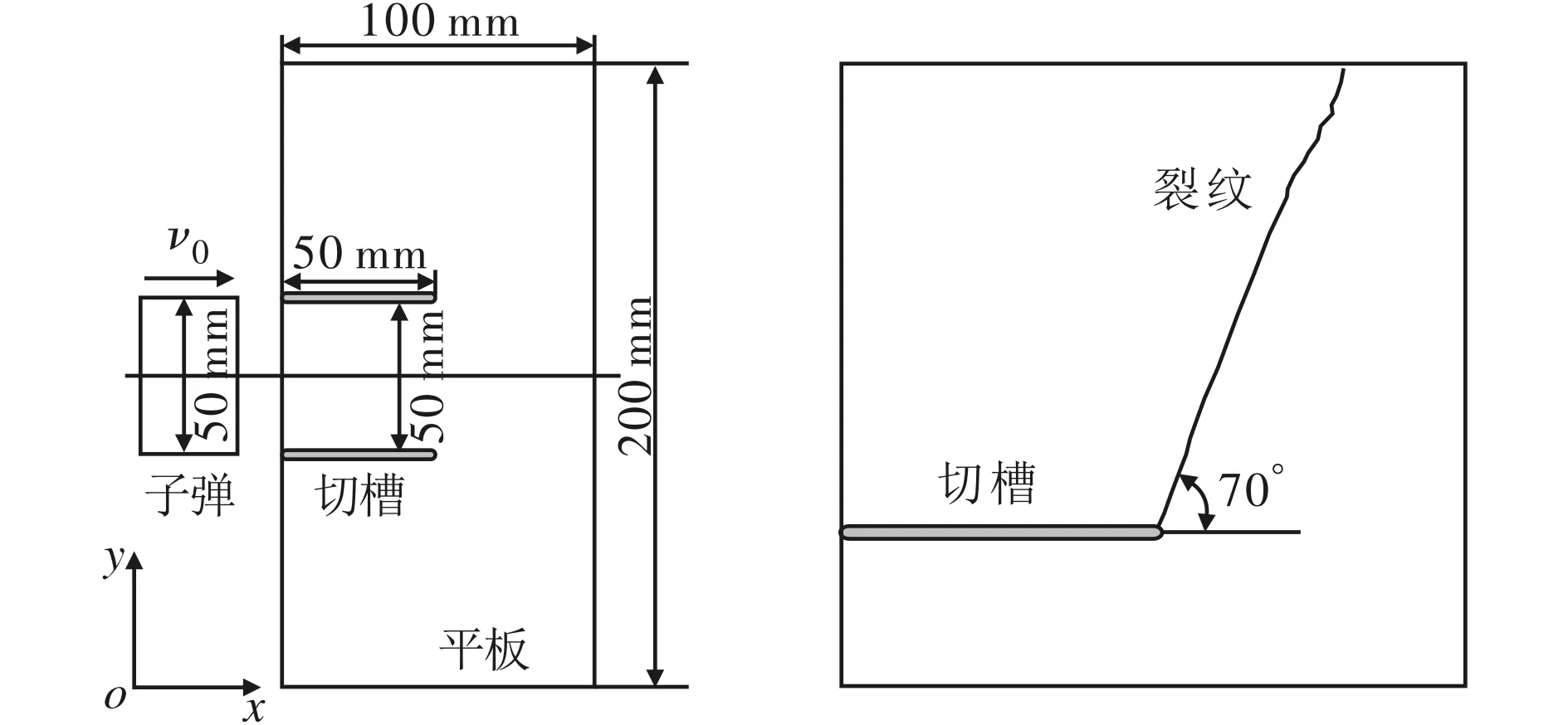
(a)实验布置示意图　(b)平板上半部分裂纹扩展路径图3　Kalthoff和Winkler的动态剪切实验

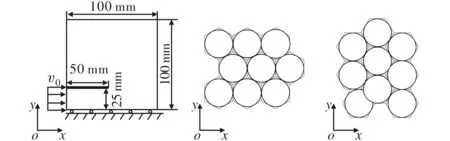
(a)　　　平板上半部分　(b)　　　六角点阵　　(c)　　　六角点阵的仿真模型　　　1型排布　　　2型排布图4　动态剪切实验的离散元建模

根据上述动态剪切实验的对称性特点,为了降低数值计算量提高计算速度,本文仅对平板上半部分进行建模仿真,如图4所示。模型中下边界受对称条件约束,下边界y方向速度vy=0 m/s,与子弹冲击接触的材料受到v0=16.5 m/s的阶跃速度扰动,模型其他边界均为自由状态。选取离散单元半径r=0.5 mm,平板上半部分的离散元模型由11 558个单元组成。为了分析单元受力时的邻近单元层数对单元排布方向的敏感性,本文选用了2种六角点阵的排布构型,如图4b、图4c所示,其中单元2型排布是1型旋转90°后的构型,2种构型下的其他离散元参数均相同。

3　仿真结果与分析

3.1　1层邻近单元

仅考虑1层邻近单元的受力作用,在六角点阵1型构型下仿真得到平板的裂纹扩展轨迹,如图5a～图5c所示。裂纹的扩展速度极快,在平板受到冲击作用后裂纹产生分叉,其中主裂纹沿x轴水平方向延伸至平板右端边界处,另一个主要裂纹沿与x轴正方向呈60°左右的角度斜向上方扩展。由图5d～图5f可以看出,采用六角点阵2型构型时,裂纹从切槽端部沿与x轴成大约45°的角度向材料右端扩展。当子弹冲击作用经历80 μs左右,有一条新的裂纹从平板右端萌生并沿x轴负方向传播。根据上述仿真结果可知,只考虑1层邻近单元的作用时,单元排布构型会严重影响到裂纹的扩展路径。

(a)　　　1型排布,　　(b)　　　1型排布,　　(c)　　　1型排布,40 μs　　　60 μs　　　80 μs

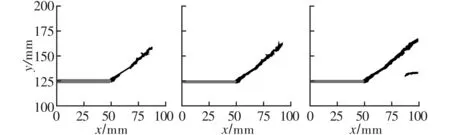
(d)　　　2型排布,　　(e)　　　2型排布,　　(f)　　　2型排布,40 μs　　　60 μs　　　80 μs图5　考虑1层邻近单元作用的裂纹扩展路径

图6给出了平板裂纹的扩展速度图,从中可以看出,在1型构型模型下仿真的裂纹从10 μs开始扩展到52 μs时结束,而在2型构型模型下仿真的裂纹扩展起止时间分别为18 μs和44 μs,并且在裂纹扩展的整个时间区间内,2种构型裂纹的扩展速度趋势相差很大。仿真结果显示,裂纹的最大扩展速度约为10 km/s,远大于材料的Rayleigh波速2 799 m/s,这与物理事实相违背。可见,仅考虑1层邻近单元的方法在研究材料的裂纹扩展问题时并不适用。

图6　考虑1层邻近单元作用的裂纹扩展速度

3.2　2层邻近单元

采用2层邻近单元搜索方法进行仿真计算,图7a～图7c为六角点阵1型排布构型下仿真得到的裂纹扩展轨迹,裂纹的传播方向大致与x轴成45°角。在2型构型下计算的裂纹扩展轨迹如图7d～图7f所示,起初裂纹沿与x轴成45°的方向传播,裂纹向右传播10 mm后产生分叉,主裂纹沿与x轴约70°方向继续传播,次裂纹沿x轴正方向延伸10 mm后止裂。

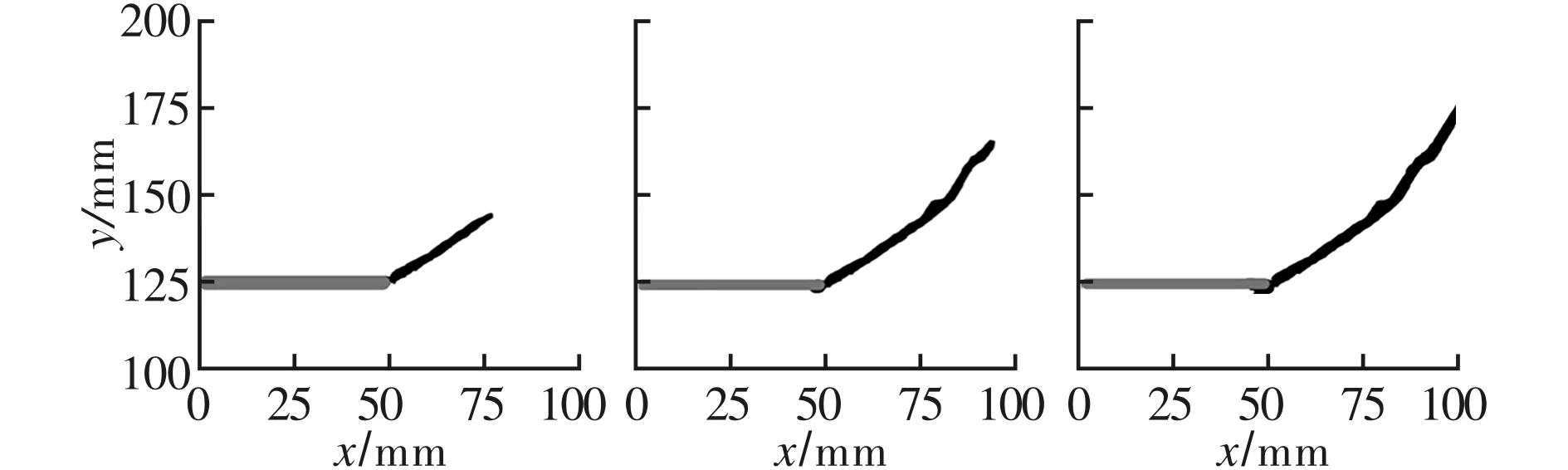
(a)　　　1型排布,　　(b)　　　1型排布,　　(c)　　　1型排布,40 μs　　　60 μs　　　80 μs

(d)　　　2型排布,　　(e)　　　2型排布,　　(f)　　　2型排布,40 μs　　　60 μs　　　80 μs图7　考虑2层邻近单元作用的裂纹扩展路径

如图8所示,由计算得到的裂纹扩展速度可知,在1型排布构型下裂纹的最大传播速度为2 700 m/s,而2型排布构型的最大传播速度为3 400 m/s,大于Rayleigh波速,说明2型排布构型下的数值计算结果失真。总体上当数值计算中考虑2层邻近单元时,1型和2型排布构型下的计算结果仍然有差别,与1层邻近单元搜索方法相比,基于2层邻近单元搜索方法的仿真结果与实验结果的符合程度虽然好很多,但是仍相差较大。

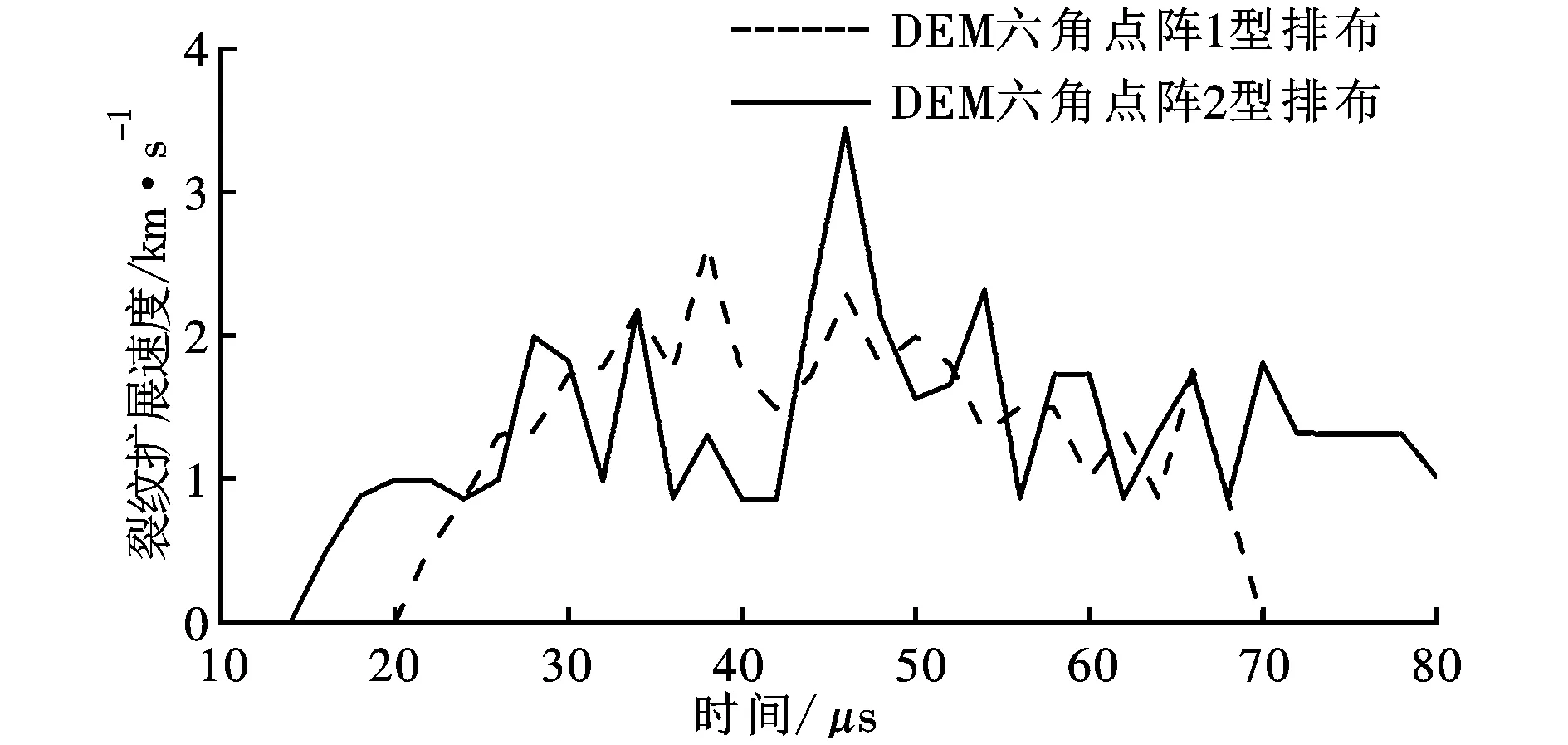
图8　考虑2层邻近单元作用的裂纹扩展速度

3.3　3层邻近单元

采用3层邻近单元搜索方法计算所得到的裂纹扩展轨迹如图9所示,可见2种不同单元排布构型的结果十分接近,裂纹均从切槽端部沿与x轴成70°的方向延伸,仿真结果与Kalthoff和Winkler的实验结果十分接近。

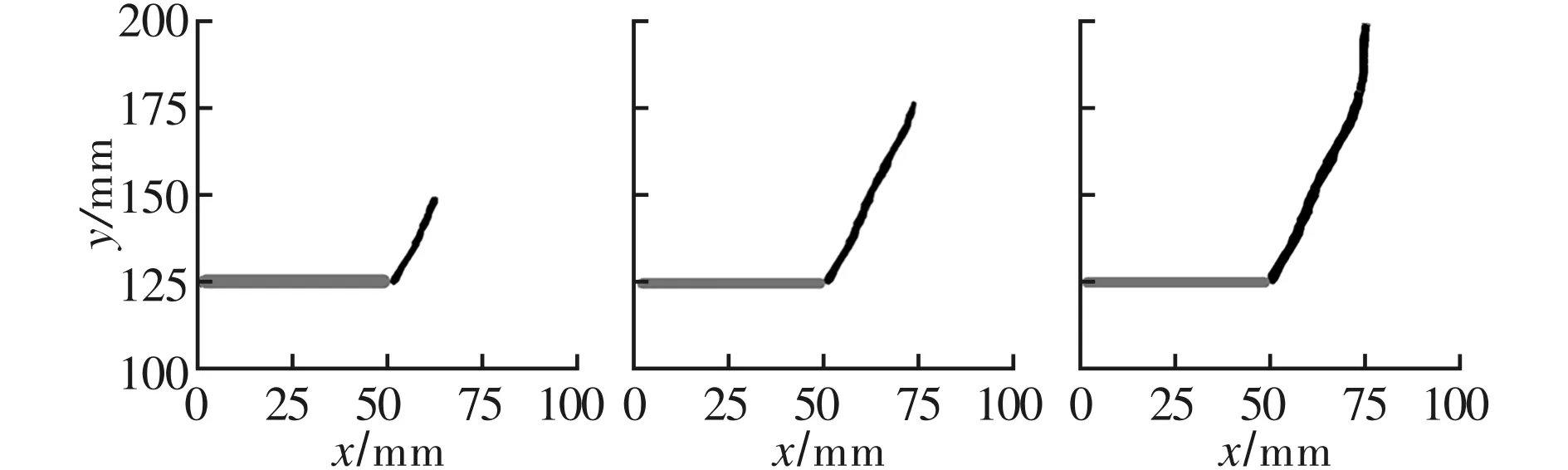
(a)　　　1型排布,　　(b)　　　1型排布,　　(c)　　　1型排布,40 μs　　　60 μs　　　80 μs

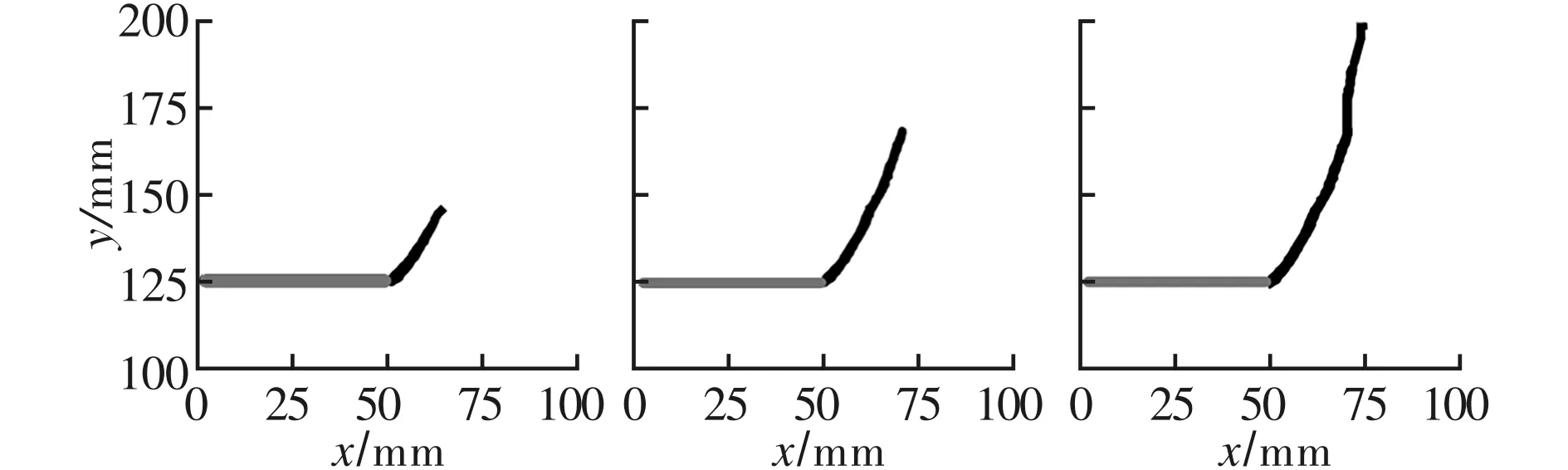
(d)　　　2型排布,　　(e)　　　2型排布,　　(f)　　　2型排布,40 μs　　　60 μs　　　80 μs图9　考虑3层邻近单元作用的裂纹扩展路径

图10给出了裂纹扩展速度图,可见在1型构型下仿真的裂纹起止时间分别为24 μs和80 μs,2型构型下仿真的裂纹起止时间为24 μs和78 μs,并且2种构型下仿真得到的裂纹扩展速度趋势也很接近,最大裂纹传播速度约为2 100 m/s,该速度值小于Rayleigh波速,符合物理事实。Belytschko等使用扩展有限元方法(XFEM)对动态剪切实验进行了仿真[21],计算得到的裂纹扩展速度如图10中实线所示,该结果与本文的仿真结果近似。以上结果说明,当采用3层邻近单元搜索算法进行离散元计算时,单元排布构型对裂纹扩展路径几乎没有影响,利用该方法可以对材料裂纹扩展问题进行有效的仿真研究。

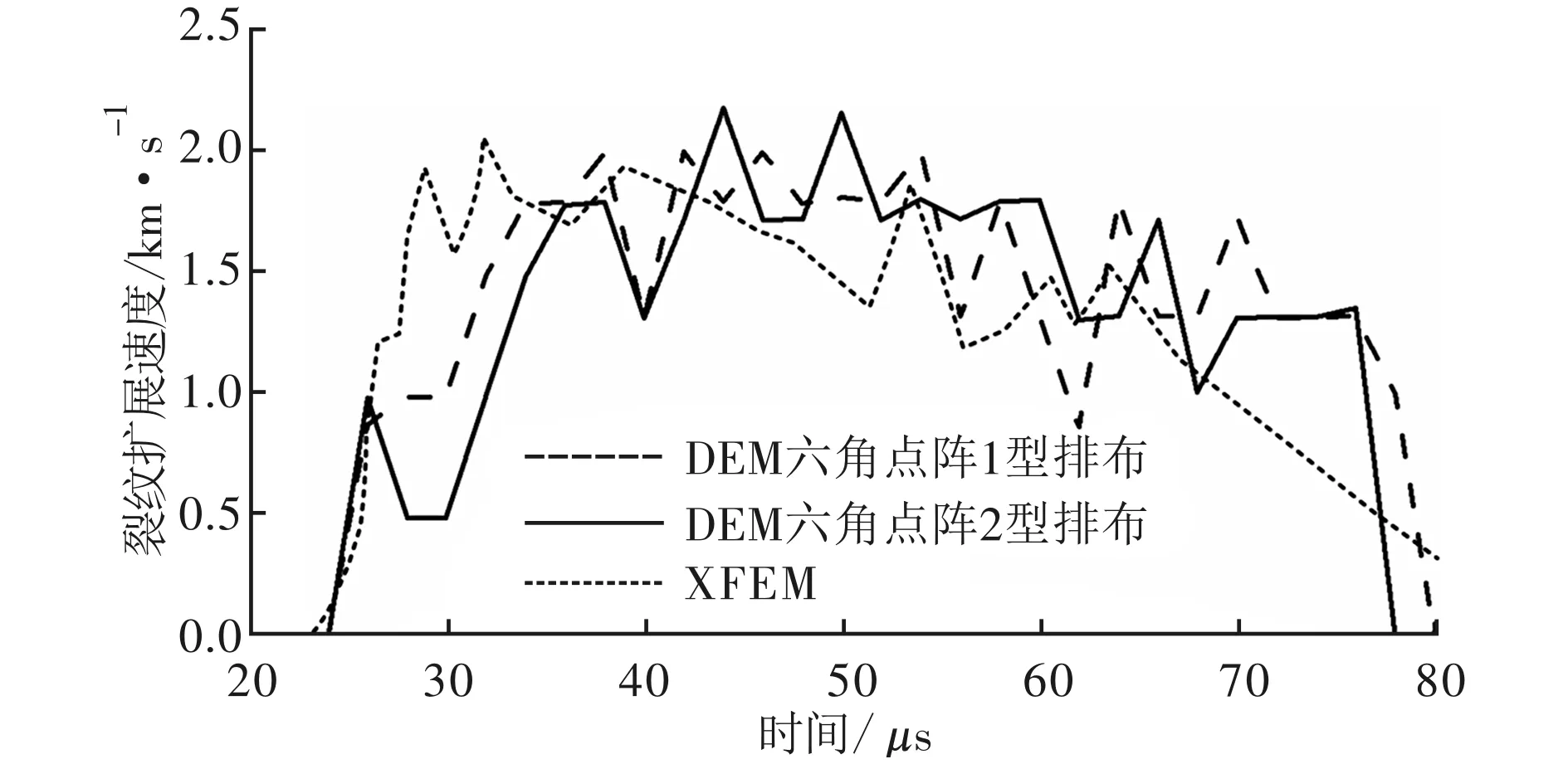
图10　考虑3层邻近单元作用的裂纹扩展速度

3.4　邻近单元层数对裂纹扩展模拟的影响分析

连结型刚体-弹簧离散元模型通过假设单元呈规则排布,对材料进行离散化网格划分。在计算过程中,如果只考虑1层邻近单元的作用,此时中心单元仅与周围6个单元间有相互作用力,即中心单元靠6个位置的弹簧共同限制其受力和运动。这个中心单元和6个弹簧建立的力学模型并不能在每个方向上表达同样的力学属性,本质上是用一种非各向同性的力学模型近似模拟各向同性材料。当分析材料断裂前的力学问题时,这种模型可以得到足够高精度的结果,但是在需要分析材料的裂纹扩展问题时,该模型的非各向同性特征就会凸显出来,导致模拟失真。

当考虑的邻近单元的层数增多时,中心单元会受到更多不同方向的弹簧的共同作用,会使模型中的非各向同性力学性质得到各向同性均化。在本文的连结型弹簧-刚度离散元模型中,取3层邻近单元可以得到有效的裂纹扩展过程的仿真结果。

4　结　论

本文研究了连结型刚体-弹簧离散元方法中参与受力计算的邻近单元层数对裂纹扩展的影响,推导了2层和3层邻近单元作用下的弹簧刚度系数和断裂判据。通过对Kalthoff和Winkler的动态剪切裂纹扩展实验进行数值仿真,发现增加邻近单元的层数可以减少单元排布构型对裂纹扩展的影响,当采用3层邻近单元搜索方法时,可以有效地模拟材料的裂纹扩展轨迹和裂纹扩展速度,因此可作为采用连结型离散元方法进一步研究材料动态断裂过程的一种手段。

参考文献:

[1]LI Shaofan, LIU W K, ROSAKIS A J, et al. Mesh-free Galerkin simulations of dynamic shear band propagation and failure mode transition [J]. International Journal of Solids and Structures, 2002, 39(5): 1213-1240.

[2]PSAKHIE S G, SHILKO E V, GRIGORIEV A S, et al. A mathematical model of particle-particle interaction for discrete element based modeling of deformation and fracture of heterogeneous elastic-plastic materials [J]. Engineering Fracture Mechanics, 2014, 130(1): 96-115.

[4]MA Wei, LI Xiangwang, DAI Lanhong, et al. Instability criterion of materials in combined stress states and its application to orthogonal cutting process [J]. International Journal of Plasticity, 2012, 30/31: 18-40.

[5]LJUSTINA G, LARSSON R, FAGERSTRÖM M. A FE based machining simulation methodology accounting for cast iron microstructure [J]. Finite Elements in Analysis and Design, 2014, 80: 1-10.

[6]MIGUÉLEZ M H, SOLDANI X, MOLINARI A. Analysis of adiabatic shear banding in orthogonal cutting of Ti alloy [J]. International Journal of Mechanical Sciences, 2013, 75(10): 212-222.

[7]MARUSICH T D, ORTIZ M. Modelling and simulation of high speed machining [J]. International Journal for Numerical Methods in Engineering, 1995, 38(21): 3675-3694.

[8]UMBRELLO D. Finite element simulation of conventional and high speed machining of Ti6Al4V alloy [J]. Journal of Materials Processing Technology, 2008, 196(1/2/3): 79-87.

[9]SALIH S, DAVEY K, ZOU Z. Rate-dependent elastic and elasto-plastic cohesive zone models for dynamic crack propagation [J]. International Journal of Solids and Structures, 2016, 90(1): 95-115.

[10] SONG J H, BELYTSCHKO T. Cracking node method for dynamic fracture with finite elements [J]. International Journal for Numerical Methods in Engineering, 2009(3): 360-385.

[11] 刘凯欣, 高凌天. 离散元法研究的评述 [J]. 力学进展, 2003, 33(4): 483-490.

LIU Kaixin, GAO Lingtian. A review on the discrete element method [J]. Advances in Mechanics, 2003, 33(4): 483-490.

[12] LIN Q, FAKHIMI A, HAGGERTY M, et al. Initiation of tensile and mixed-mode fracture in sandstone [J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(3): 489-497.

[13] SADD M H, ADHIKARI G, CARDOSO F. DEM simulation of wave propagation in granular materials [J]. Powder Technology, 2000, 109(1/2/3): 222-233.

[14] CHENG Ming, LIU Weifu, LIU Kaixin. New discrete element models for elastoplastic problems [J]. Acta Mechanica Sinica, 2009, 25(5): 629-637.

[15] WANG G, AL-OSTAZ A, CHENG A H, et al. A macroscopic-level hybrid lattice particle modeling of mode-I crack propagation in inelastic materials with varying ductility [J]. International Journal of Solids and Structures, 2009, 46(22/23): 4054-4063.

[16] TAVAREZ F A, PLESHA M E. Discrete element method for modelling solid and particulate materials [J]. International Journal for Numerical Methods in Engineering, 2007, 70(1): 379-404.

[17] WANG G, OSTOJA-STARZEWSKI M. Particle

modeling of dynamic fragmentation: ITheoretical considerations [J]. Computational Materials Science, 2005, 33(4): 429-442.

[18] SILLING S A, EPTON M, WECKNER O, et al. Peridynamic states and constitutive modeling [J]. Journal of Elasticity, 2007, 88(2): 151-184.

[19] CHEN Hailong, LIN Enqiang, JIAO Yang, et al. A generalized 2D non-local lattice spring model for fracture simulation [J]. Computational Mechanics, 2014, 54(6): 1541-1558.

[20] KALTHOFF J F, WINKLER S. Failure mode transition at high rates of shear loading [C]∥Proceedings of the International Conference on Impact Loading and Dynamic Behavior of Materials. Oberursel, Germany: IFAM, 1987: 185-195.

[21] BELYTSCHKO T, CHEN Hao, XU Jingxiao, et al. Dynamic crack propagation based on loss of hyperbolicity and a new discontinuous enrichment [J]. International Journal for Numerical Methods in Engineering, 2003, 58(12): 1873-1905.