小型H型垂直轴风力机变桨机构的优化设计与试验

张立军, 马东辰, 赵昕辉, 米玉霞, 张松, 王旱祥, 范淑琴

(1.中国石油大学(华东)机电工程学院, 266580, 山东青岛; 2.中国石油大学(华东)化学工程学院, 266580, 山东青岛; 3.西安交通大学机械工程学院, 710049, 西安)

风电是资源潜力大、技术成熟的可再生能源。近年来,世界风力发电能力快速增长,过去10年平均每年增长30%左右。据预测,到2020年,风能发电量将达到世界能源消费需求的5%[1]。我国可开发利用的风能资源十分丰富,在国家政策措施的推动下,我国的风电产业进入稳定持续增长的新阶段[2]。垂直轴风力机以其无需对风、易于安装等优点,越来越受到人们的关注,但其风能利用率较低,目前垂直轴风力机的风能利用率仅为30%～35%,而利用双致动盘理论得出的垂直轴风力机的最大风能利用率高达64%[3],因此垂直轴风力机仍有较大改进空间。

目前,对于提高垂直轴风力机风能利用率的方法尚处于研究阶段。姬俊锋等利用正交设计方法,给出了特定条件下遮蔽-增速板安装角及其安装位置半径等参数的最佳值,并通过数值仿真得出带遮蔽-增速板的H型风力机可以高效合理地收集风能,减少风能做负功,提高了整体的风能利用率[4];廉正光等利用双曲柄调距机构及双偏心轴机构,通过周期性改变垂直轴风力机的桨距角来提升风能利用系数,并制造出采用该机构的风力发电机样机[5-6];赵振宙等采用扰流技术,通过适当增大局部扰流角的方式来提高风力机的整体性能[7];Sagharichi等通过数值模拟发现给定条件下当桨距角β=-3°时可有效地提高风力机的风能利用率系数,并制作了变桨距垂直轴风力机样机[8]。

上述研究提出的方法对垂直轴风力机风能利用率的提高均能起到一定效果,但大多都是侧重于提出解决方案,而对变桨规律的获取缺少理论解释,对变桨方法的优化分析缺少研究。由于叶片攻角随方位角不断变化是垂直轴风力机风能利用率低的主要原因[9],本文通过调节叶片桨距角来控制攻角的变化,重点对H型垂直轴风力机自动变桨机构进行研究,并给出了一种优化设计方法。

1　桨距角调节策略的制定

1.1　叶片理论最佳攻角求解

本文所研究的1 kW H型垂直轴风力机的相关参数如表1所示,叶片采用对称翼型NACA0015。

表1　垂直轴风力发电机的相关参数

对垂直轴风轮的分析模型如图1所示。其中:W为来流风速V和叶片旋转线速度Rω的合成风速;ω为风轮旋转角速度;θ为叶片方位角,当θ=0°～180°时称为上风区,当θ=180°～360°时称为下风区;α为叶片攻角,是合成风速方向与叶片弦线方向的夹角;β为叶片桨距角,是叶片旋转线速度方向与叶片弦线方向的夹角;FL和FD分别代表叶片受到的升力和阻力,将FL和FD沿风轮旋转的切向和法向正交分解,可得到叶片受到的切向力FT和法向力FN,其中切向力FT是推动风轮运转的主动力。

下面重点讨论升力驱动风轮产生最大切向力时的叶片攻角。

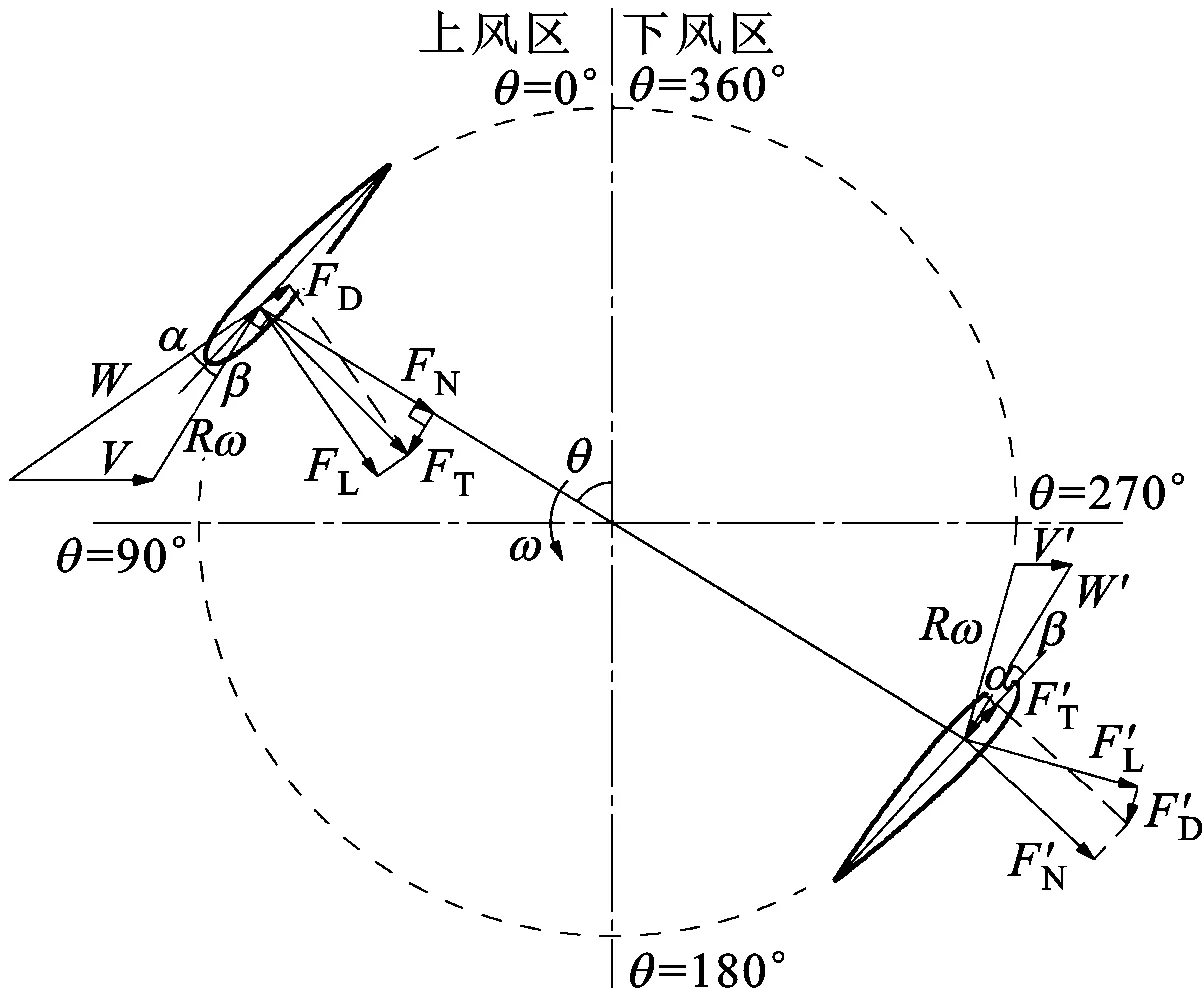
图1　叶片受力分析图

通过分析图1中的速度关系,可以得出垂直轴风力机叶片攻角的表达式[3]为

(1)

式中:λ为风轮的局部叶尖速比

(2)

叶片所受切向力为

FT=0.5ρCTcHW2

(3)

式中:ρ为空气密度,在标准大气压下其数值常取1.225 5 kg/m3;c为叶片弦长;H为风轮高度;CT为切向力系数,是翼型的升力系数CL和阻力系数CD在弦长方向的合成值,其计算式为

CT=CLsinα-CDcosα

(4)

由式(3)可知,当切向力系数最大时,风轮可以获得最大切向力。根据NACA系列翼型特性数据库可得到NACA0015翼型在Re=2.0×105时各攻角对应的升阻力系数值,同时利用式(4)可以得到切向力系数随叶片攻角的变化,如图2所示。

由图2可知,在切向力系数取最大值时,风轮上风区的攻角是10.7°,根据对称翼型升阻力系数的对称性,可知下风区的攻角是-10.7°。由于存在图2中所示的失速区,根据已有经验[10-11],为使叶片在旋转过程中不过多进入失速区,攻角的合理取值可向正常工作区方向偏离2°～3°。为了方便下文风力机结构的设计与计算,分别取上风区理论最佳攻角为8°,下风区理论最佳攻角为-8°。

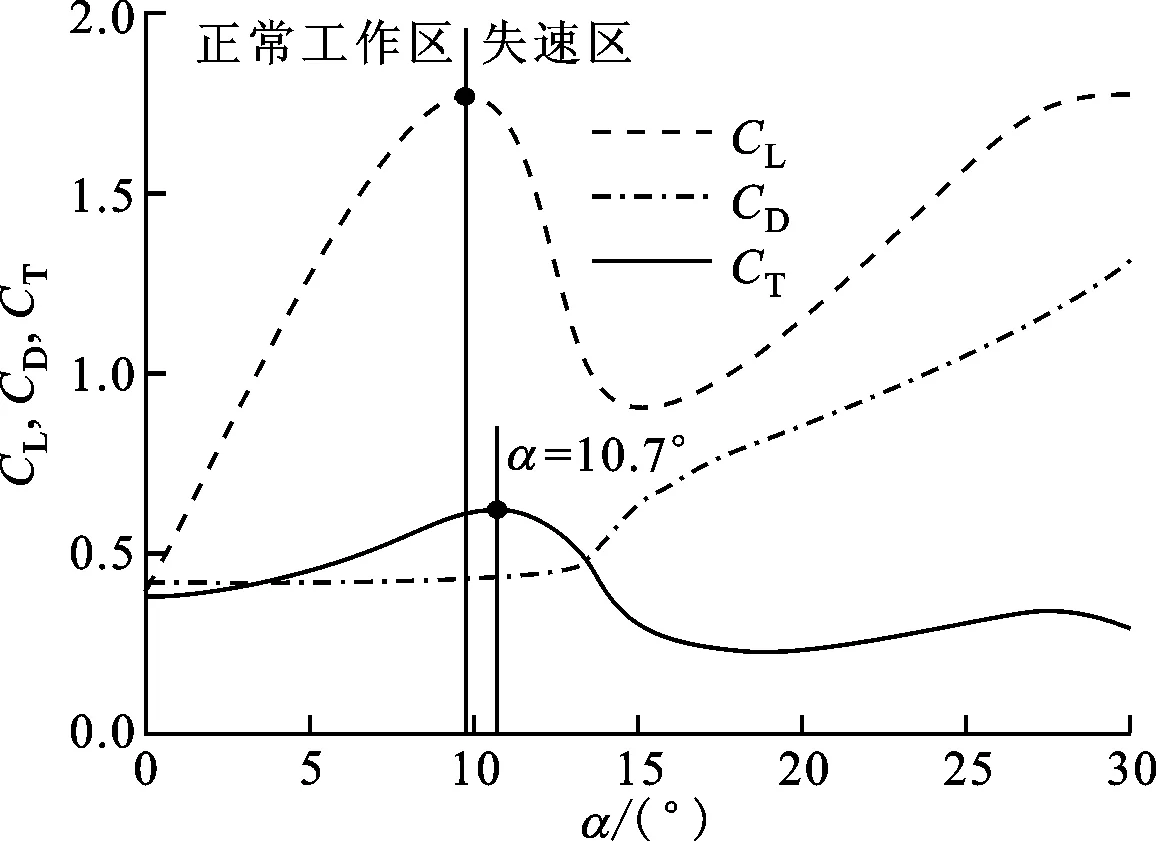
图2　NACA0015翼型气动参数随叶片攻角的变化

1.2　桨距角调节策略

由于叶片在整周旋转时其攻角很难直接测出,所以实际操作中采取调节桨距角的方式达到调节攻角的目的。其中,叶片桨距角的计算公式如下

(5)

令式(5)中α=8°,使攻角始终等于理论最佳攻角值,得到叶片在上风区旋转过程中的桨距角调节规律;同理,令α=-8°得到叶片在下风区的桨距角调节规律。在λ=2时,求得不同方位角下桨距角的数值如表2所示。

表2　不同叶片方位角所对应的桨距角

根据表2中的对应关系,利用MATLAB软件拟合出桨距角与方位角间的关系如下式所示

β(θ)=-2.577×10-18θ9+4.174×10-15θ8-

2.781×10-12θ7+9.793×10-10θ6-

1.953×10-7θ5+2.207×10-5θ4-0.001 359θ3+

0.040 35θ2-0.106 9θ-7.543

(6)

该多项式用于实现下文优化设计中作为桨距角实时调节策略的理想曲线。需要说明的是:对于本文所研究的垂直轴风力机,在现有给定参数下,当λ=2时,风力机具有较好的气动性能[12],所以选取λ=2时为例,求解叶片桨距角调节策略,而在其他局部叶尖速比条件下,桨距角调节策略的求解方法均相同,在此不再一一列出。

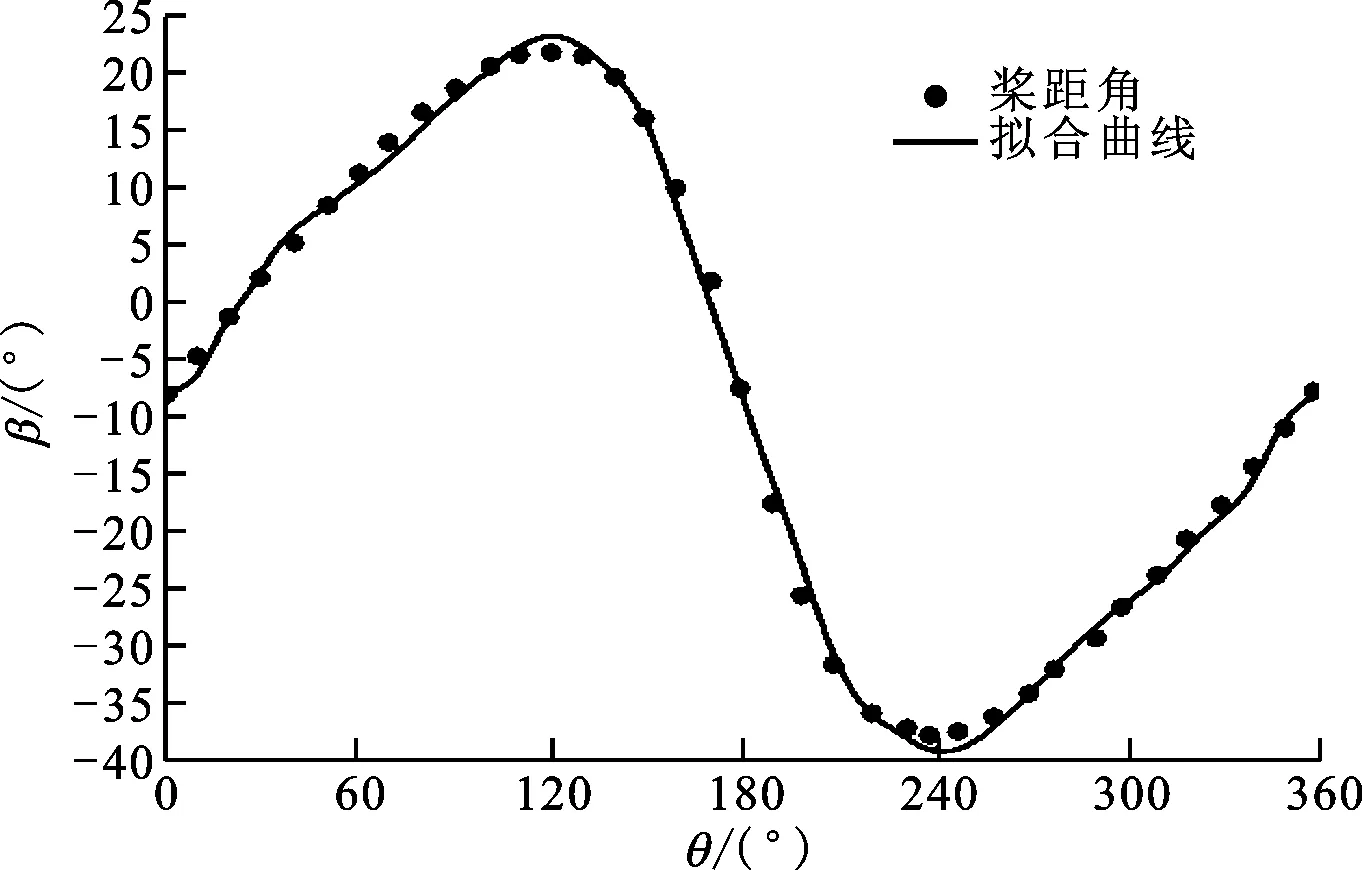
图3　桨距角与方位角拟合曲线

利用式(6)中桨距角调节规律,得到叶片整周旋转过程中桨距角变化的拟合曲线如图3所示。由图3可知,桨距角随方位角的变化趋势呈类正弦规律,且该拟合曲线与实际桨距角符合程度较高。

2　变桨机构的设计与优化

叶片桨距角调节策略确定后,为了在实际工作过程中使叶片桨距角最贴近所拟合的桨距角调节曲线,需要设计出对应的机械结构,以实现风力机在不同风速下的变桨规律。

2.1　双曲柄变桨机构

本文设计的变桨距垂直轴风力机模型如图4所示,主要由叶片、支撑杆、主轴、变桨机构等组成,其中变桨机构置于垂直轴风力机上端,由推杆、支撑杆、叶片弦长、支架组成。

为使垂直轴风力机在整周旋转过程中桨距角按类正弦规律发生周期性变化,且能满足结构紧凑、传动可靠等要求,变桨机构选用双曲柄机构作为设计原型,通过优化计算获得各个连杆长度,以实现调节桨距角的目的。

垂直轴风力机的双曲柄变桨机构的工作原理如图5所示。其中:杆OA是双曲柄变桨机构的机架,在风向风速不变时杆OA一直保持如图5所示的位置,且长度不变;杆OC作为叶片的支撑杆,运转过程中始终保持不变;BC是叶片弦长,作为两曲柄之间的连杆;杆AB是推杆,它是实现叶片桨距角变化的杆,在风力机做整周旋转时杆AB通过A、B两点的转动副带动叶片BC绕C点旋转,从而实现叶片桨距角的变化。

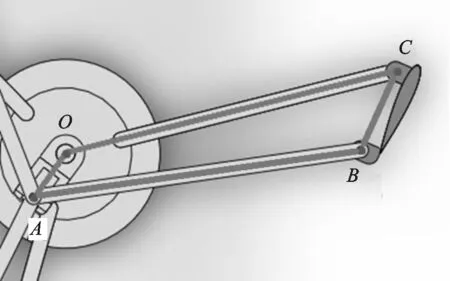
图5　双曲柄变桨机构原理图

2.2　变桨机构优化分析与计算

双曲柄变桨机构的几何关系如图6所示。其中:φ为支撑杆OC与叶片弦长BC间的夹角;γ为机架安装角;OC长度b和BC长度c是已知固定参数。选取推杆AB的长度d、机架OA的长度a以及γ作为约束变量,通过以上约束条件以及结构中所存在的数学关系可得到目标函数。

对于垂直轴风力机,其连杆机构用于控制叶片的角度,不传递动力,故为简化计算,机构压力角和传动角可暂时不加考虑,仅考虑连杆的角度变化与所设计的桨距角调节方案的一致性,将机构旋转一周的过程中实际桨距角与理想桨距角的平方差作为目标函数,以该目标函数最小为优化目标建立数学模型,并根据图6中的几何关系推导出实际桨距角的变化规律。

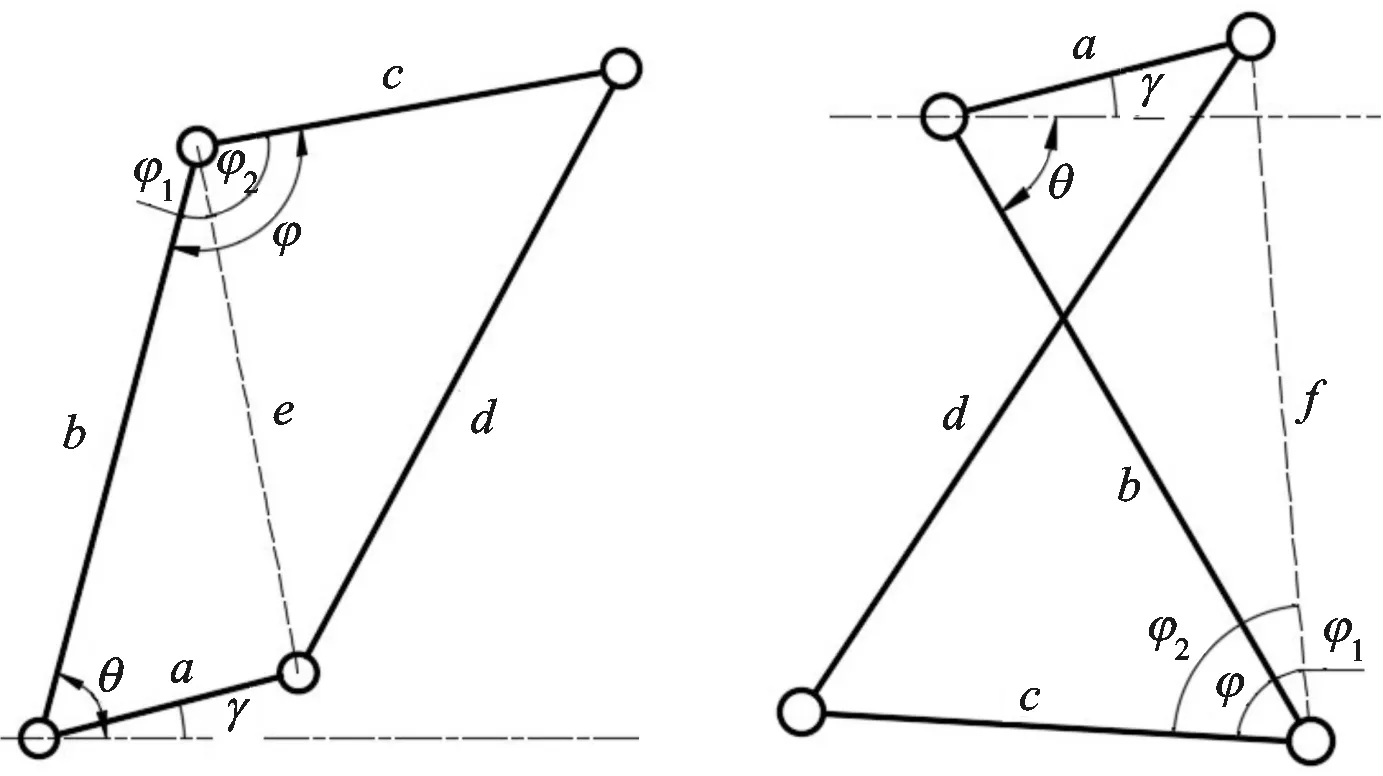
图6　变桨机构几何分析图

叶片方位角为(0°,180°)时,有

(7)

叶片方位角为(180°,360°)时,有

(8)

最终得出机构优化目标函数为

f(a,d,γ,θ)=‖φ(θ)-β(θ)‖2

(9)

式中:φ(θ)表示实际桨距角,其计算公式为

(10)

约束条件是根据设计中各参数的限制条件确定的,而在本节所研究的双曲柄变桨机构优化设计中,首先要满足组成双曲柄机构的基本条件:每根杆的杆长大于0而且满足杆长条件,且为便于后期控制,γ应处于0°～25°之间为宜,即

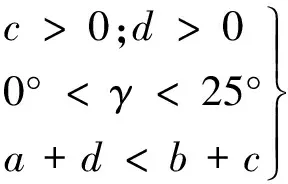
(11)

双曲柄结构的优化问题属于约束优化,约束优化的随机方向法和复合形法等在迭代计算中不需要计算导数,由于随机方向法比复合形法计算简单且适用于维度不高的中小型优化问题,而本次优化设计的变量维数为3,属于低维小型优化问题,所以选取随机方向法作为本文的优化方法进行计算[13]。随机方向法的计算流程如图7所示。

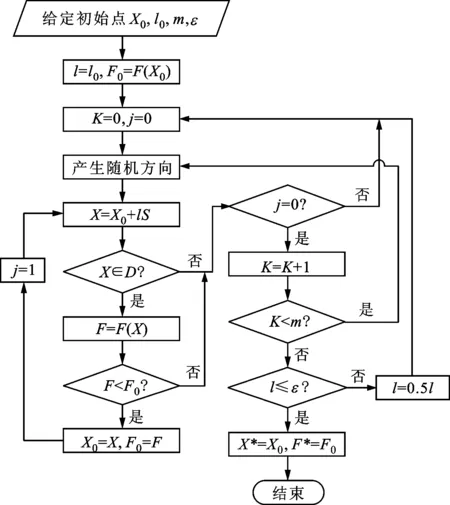
图7　随机方向法程序流程图

在可行域内取初始点为

(12)

取步长l=0.1、收敛精度ε=0.001,对应于每一个叶尖速比,经过12次迭代,得到其最优解,计算结果如表3所示。

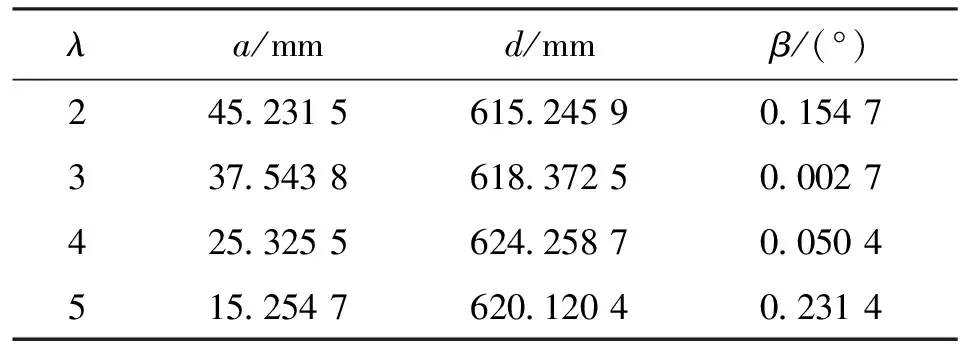
表3　不同叶尖速比下各参数最优解

注:a、d、β的初始值分别为50 mm、600 mm、0°。

由表3可知,在叶尖速比变化时,d和β变化不大,故在实际工作中仅调整a,同时为了变桨机构加工方便,a均取整数,在λ=2下,取a=45 mm。

3　ADAMS仿真与结果分析

为验证双曲柄变桨机构设计的合理性,通过计算得出各个叶尖速比下对应的双曲柄参数最优解后,根据已知参数和求得的参数进行建模仿真,所建立的ADAMS仿真模型如图8所示。

图8　ADAMS动力学仿真模型

仿真过程中不考虑由于局部叶尖速比的改变所带来的机架长度的微变化,故仿真时使用λ=2时的支架滑块位置,利用ADAMS的布尔加操作使支架滑块与滑槽通过主轴固定在底座上,然后将此合成底座使用固定副作为相对地面静止的底座。在仿真控制界面,设定结束时间为500 s,步数设为1 500,其他参数使用默认设置。在此基础上,得到推杆和叶片的位置曲线分别如图9和图10所示。

图9　3个推杆的位置曲线

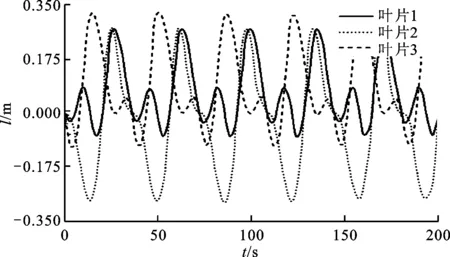
图10　3个叶片的位置曲线

由图9可知,3个推杆的位置呈周期性变化且各推杆的运动轨迹相同,故在一个周期内的某一个特定点,3个叶片经过此点时的运动形态相同,而且在整周旋转时每个特定点处叶片都有一个对应的最佳形态以实现变桨功能。由图10可知,3个叶片的运动也是周期性变化的,不过由于起始位置不同,3个叶片位移的极值稍有差别。

为验证叶片实际工作中桨距角的变化与理想桨距角曲线的吻合程度,利用旋转测角法对不同方位角下的桨距角进行测量,具体操作如图11所示。

图11　桨距角实际测量图

利用图11所示位置,可以测得3组对应方位角下的桨距角,这样每隔10°变换一次叶片位置,可得到不同方位角下的桨距角大小,如此重复12次可得到36个数据点,将这些数据点拟合并与理想桨距角曲线作对比,得到的结果如图12所示。

从图12中可以看出:叶片实际工作中,实际桨距角曲线与理想桨距角曲线的整体吻合程度较高,尤其是在垂直轴风轮上风区内;在风轮下风区230°～360°内,桨距角曲线与理想桨距角曲线发生了细微偏离,这主要是因为垂直轴风轮下风区诱导速度的大小和方向均发生了不同程度的变化所致,其计算和求解过程非常复杂[3],目前此类计算过程中大都忽略了下风区诱导速度的变化。

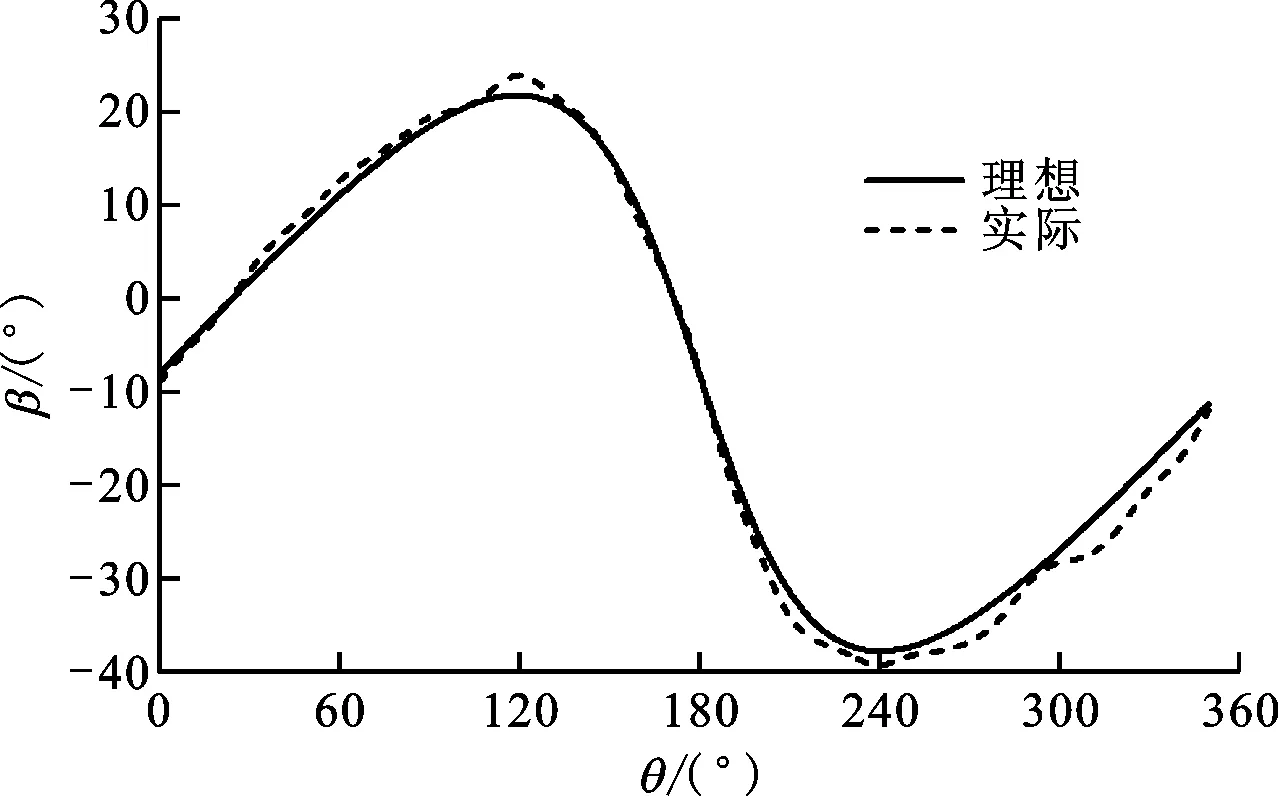
图12　实际桨距角与理想桨距角曲线对比图

4　风洞试验

根据上述优化设计结果,研发的1 kW H型变桨距垂直轴风力机试验装置如图13所示,其工作原理是:电动推杆伸出长度相当于图5中的杆OA,

即

变桨机构中机架的长度,不同风速条件下,根据优化计算结果,调节电动推杆的伸出长度,带动调节推杆牵引叶片摆动,以实现叶片桨距角的变化。试验时,将来流风向与尾舵指示方向平行时作为变桨策略的调节基准,尾舵可实现风力机实时对风。当风向发生变化时,尾舵也随风转动,使来流风向始终与尾舵指示方向平行,保证变桨策略始终在调节基准上进行,以适应风向的变化。本次风洞试验是在学校自制风洞中完成的,该风洞的风由镶嵌在水泥墙壁上的16台轴流风机提供,每台风机皆由变频电机控制,风洞产生的风速能够连续可调,可实现的试验风速范围为2～10 m/s。

通过风洞试验并与传统定桨距垂直轴风力机进行对比,得到两种垂直轴风力机在不同风速下的发电功率如表4所示。由表4可知,变桨距垂直轴风力机具有良好的自启动性能,能在风速2 m/s时启动。更为重要的是,在同等风速下,变桨距垂直轴风力机的发电功率均高于定桨距垂直轴风力机,在现有风速条件下,变桨距垂直轴风力机发电效率较定桨距风力机至少高7.86%。

表4　两种风力机发电功率对比

1:调节推杆;2:尾舵;3:电动推杆;4:发电机图13　变桨距垂直轴风力机

5　结　论

(1)通过对垂直轴风力机风轮气动特性分析,取叶片的合理攻角值上风区为8°,下风区为-8°,并获得了理想桨距角的变化曲线。

(2)使用随机方向法对所设计的双曲柄变桨结构进行了优化设计,得出了不同叶尖速比下实时变桨机构的参数优化值。

(3)变桨机构运动学特性仿真结果表明,实际桨距角曲线与理想桨距角曲线的整体贴合程度较高,验证了本文设计的实时变桨机构是可行性的。

(4)风洞试验结果进一步表明,变桨距垂直轴风力机具有更好的自启动性能和更高的发电效率,且在试验风速范围内,发电效率较定桨距垂直轴风力机至少提高7.86%。

参考文献:

[1]LEUNG D Y C, YANG Y. Wind energy development and its environmental impact: a review [J]. Renewable & Unstainable Energy Reviews, 2012, 16(1): 1031-1039.

[2]郭显义. 分析风力和太阳能光伏发电现状及发展趋势 [J]. 中国商界, 2012(10): 421-421.

Guo Xianyi. Analysis of the status and development trends of wind power and solar photovoltaic power generation [J]. Chinese Business Community, 2012(10): 421-421.

[3]伊恩帕拉斯基沃尤. 垂直轴风力机原理与设计 [M]. 李春, 等译. 上海: 上海科学技术出版社, 2013: 124-140.

[4]姬俊峰, 邓召义, 蒋磊, 等. 5 kW遮蔽-增速升力型垂直轴风力机优化设计 [J]. 工程热物理学报, 2012, 33(7): 1139-1142.

JI Junfeng, DENG Shaoyi, JIANG Lei, et al. Optimization design of a 5 kW lift type vertical axis wind turbine with wind shield-growth patterns [J]. Journal of Engineering Thermophysics, 2012, 33(7): 1139-1142.

[5]廉正光. 采用双曲柄调距机构的垂直轴风力发电机机理研究与样机设计 [J]. 机械设计, 2016, 33(8): 100-104.

LIAN Zhengguang. Principle research and prototype design of a vertical axis wind turbine with double crank adjustment mechanism [J]. Journal of Machine Design, 2016, 33(8): 100-104.

[6]廉正光, 张宏伟, 李恺. 一种变桨距垂直轴风力发电机: 201410009955.3 [P]. 2014-03-26.

[7]赵振宙, 陈潘浩, 王同光, 等. 基于扰流技术的直叶片升力型垂直轴风轮的性能改善 [J]. 机械工程学报, 2016, 52(22): 146-152.

ZHAO Zhenzhou, CHEN Fanhao, WANG Tongguang, et al. Performance improvement of lift type wind turbine with straight blades based on interference airflow technology [J]. Journal of Mechanical Engineering, 2016, 52(22): 146-152.

[8]SAGHARICHI A, MAGHREBI M J, ARABGOLARCHEH A. Variable pitch blades: an approach for improving performance of Darrieus wind turbine [J]. Journal of Renewable & Sustainable Energy, 2016, 8(5): 111103.

[9]NOBUYUKI F, SATOSHI S. Observations of dynamic stall on Darrieus wind turbine blades [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89(2): 201-204.

[10] BHUTTA M M A, HAYAT N, FAROOQ A U, et al. Vertical axis wind turbine: a review of various configurations and design techniques [J]. Renewable & Sustainable Energy Reviews, 2012, 16(4): 1926-1939.

[11] LEE C H, MIN S Y, PARK C J, et al. Optimal design and verification tests of cycloidal vertical axis wind turbine [J]. Journal of Renewable & Sustainable Energy, 2015, 7(6): 433-440.

[12] PARKER C M, LEFTWICH M C. The effect of tip speed ratio on a vertical axis wind turbine at high Reynolds numbers [J]. Experiments in Fluids, 2016, 57(5): 74.

[13] 陶栋材. 现代设计方法学 [M]. 北京: 国防工业出版社, 2012: 47-53.