考虑微凸体相互作用的确定性接触模型

王庆朋, 张力, 陈斌, 耿杨涛

(1.重庆大学汽车工程学院, 400044, 重庆; 2.河南农业大学机电工程学院, 450002, 郑州)

在机械系统中,粗糙表面的接触特性是系统动态特性、摩擦与磨损、疲劳与失效以及全寿命周期等分析的基础,并且将日益广泛地成为关键科学技术问题,与之相应地,如何考虑微凸体相互作用也变得愈加重要。

目前,研究粗糙表面接触的方法主要有概率统计、分形理论、数值计算和确定性理论等。在概率统计方法中,常将微凸体视为比较简单的几何模型,然后利用特定的概率密度函数将其拓展到整个粗糙表面,如经典的GW[1]和BGT[2]等模型。在已有研究中更多地是处理为单个球体简单地叠加,忽略相互作用的影响,这显然不符合实际接触情况。Ciavarella等基于GW模型,通过改变名义接触压力来考虑微凸体相互作用,该方法等价于增加两作用面间的间隔,文中也指出,只适用于中等载荷的分析[3]。Afferrante等利用高斯曲率的一阶和二阶近似,当微凸体发生相互作用时,将相邻两个微凸体曲率的几何平均值视为新生成微凸体的曲率,由于要采用坐标点对曲率进行计算,这将需要更多的计算成本[4]。在分形理论中,利用具有尺度独立性的分形参数来表征粗糙表面以及相应的接触特性,忽略微凸体间的相互作用[5]。在数值计算方法中,杨楠等利用有限元方法对多粗糙峰进行分析,发现中心接触区的变形受到相邻一定数目粗糙峰的影响[6]。Hyun等采用同样的方法对粗糙表面建立精确的弹性、无摩擦接触模型,小至离散尺度,对接触面积和接触压力进行分析,事实上,接触面积被过高地估计[7]。文献[8]利用离散位错塑性的方法考虑微凸体相互作用,对一个等间距正弦表面压缩,结果表明,考虑相互作用的微凸体发生平坦化所需要的接触压力要比未考虑的大。数值方法可以最大程度地逼近真实接触情况,Persson对此指出,如果考虑宏观器件到微观原子,可能包括约7个数量级,对应1021个自由度,进行计算显然是不现实的[9]。对于确定性接触模型,作者对已有微凸峰确定准则进行总结,指出等效峰中可能存在不连续、重叠、丢失和半径过小而被“吞没”等问题,并且提出“谷-峰-谷”模式的确定准则[10]。在已有的确定性接触模型中未考虑微凸体相互作用。

目前,在接触问题的研究中存在的主要限制是:①在接触过程中,微凸峰的曲率半径始终保持不变,事实是否如此;②如何考虑相邻微凸体间的相互作用。事实上,在两粗糙表面相互作用过程中,微凸体的大小和分布不可能是一成不变的,它们之间发生着物理的、化学的和力学的等综合作用,必然会引起相应状态的变化。再者,从动态的观点来看,未包含微凸体相互作用的接触模型是不完整的。鉴于此,本文在“谷-峰-谷”模式微凸峰确定性接触模型的基础上,通过引入几何重叠和固体表面能来考虑微凸体相互作用,并且根据材料体积守恒原理对其进行合并,在此基础上分析粗糙表面接触特性的变化规律。

1　模型的建立

1.1　单个微凸体接触模型

对于单个微凸体的接触,作者在文献[11]中将微凸体的弹性和塑性接触状态拓展到整个接触过程,提出混合弹塑性接触模型。单个球体的接触面积和接触力分别为

A=f1(δ)(πrδ)+f2(δ)(2πrδ)

(1)

(2)

式中:E和r分别为等效弹性模量和球体半径;δ为法向变形量;p0为塑性状态下的平均接触应力;f1(δ)和f2(δ)分别为弹性和塑性状态的比例系数(详细证明过程见文献[11])

(3)

其中n为Meyer硬度指数,δy和δp分别为初始屈服点和完全塑性屈服点对应的法向变形量。

1.2　粗糙表面轮廓

采用分形理论获得一组二维粗糙表面轮廓,采样长度为800 μm、采样间隔为0.5 μm时的粗糙度(算术平均偏差Ra和均方根偏差Rq)如表1所示。

表1　表面轮廓的粗糙度

利用文献[10]中提出的“谷-峰-谷”模式的微凸峰确定准则得到单个球体,进而得到连续等效粗糙表面轮廓,如图1所示。

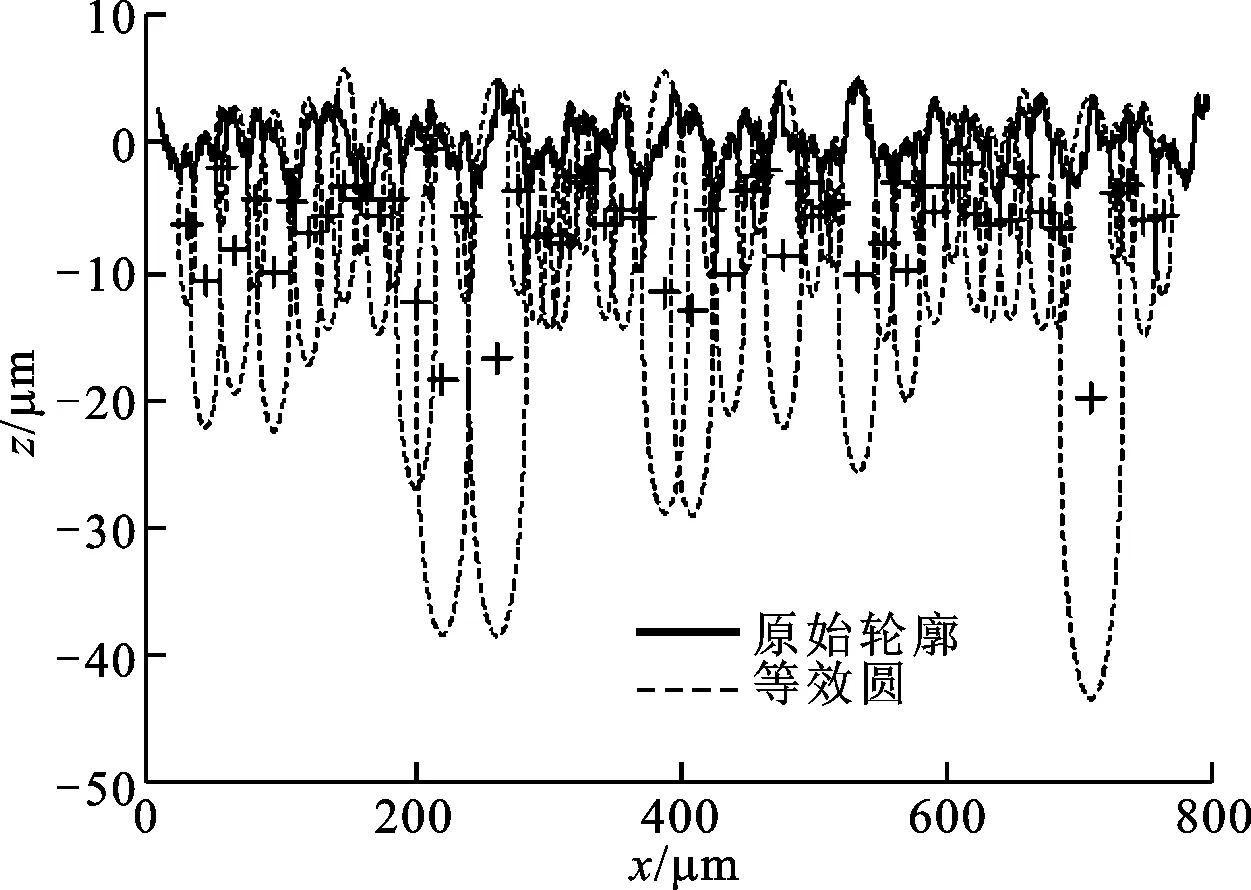
图1　粗糙表面轮廓及其等效峰

1.3　微凸体相互作用

粗糙界面作为一个系统,其各尺度对应的组成部分如零件表面结构、微凸体、材料晶体、分子和原子等,无不处于运动和变化之中,这将引起表面形貌的重构。固体表面能是由于表面分子间化学键遭到破坏,使表层原子朝向体相外侧的键能无法得到补偿而使其具有额外的能量。虽然固体表面能和表面张力的涵义不同,但是具有相等的数值,对于二维表面轮廓,也可以理解为改变单位长度所需要的力。

固体介质表面形貌的变化与地球板块运动有着相似的变化规律,只是尺度上存在差异。地球上的板块并不是简简单单地漂移,而是包括碰撞、挤压和俯冲等相互作用。如果能够理解青藏高原是由欧亚板块和印度洋板块相互作用造成的,那么相邻微凸体间必然发生同样的作用。事实上,相邻微凸体在压缩过程中发生平坦化,结合在一起就如形成一个大的微凸体,进而承受更大的外载荷。

为了使分析得以简化,当出现几何重叠和超过固体表面能时将导致“大山峰”的形成。为了有效地表征相邻微凸体间的合并,增加如下约束条件

(4)

式中:xc为等效圆圆心的横坐标值;rc为接触圆半径;μ为摩擦系数;xol为重叠长度;γsv为固体表面能。

当满足条件时,利用面积相等将发生相互作用的等效圆进行合并,有

π(r′(k))2=π(r(k))2+π(r(k+1))2

(5)

式中:r′为新生成圆的半径。

图2为等效粗糙峰及其重叠后合并的示意图。计算得到新生成圆的半径后,再利用合并前相邻两圆变形后的左右端点A、B,构成三角形AO′B,如图2中粗实线所示,利用三角形外接圆可确定新生成圆的圆心位置和峰高度,这为下一个压缩步长提供了一个新的表面轮廓。

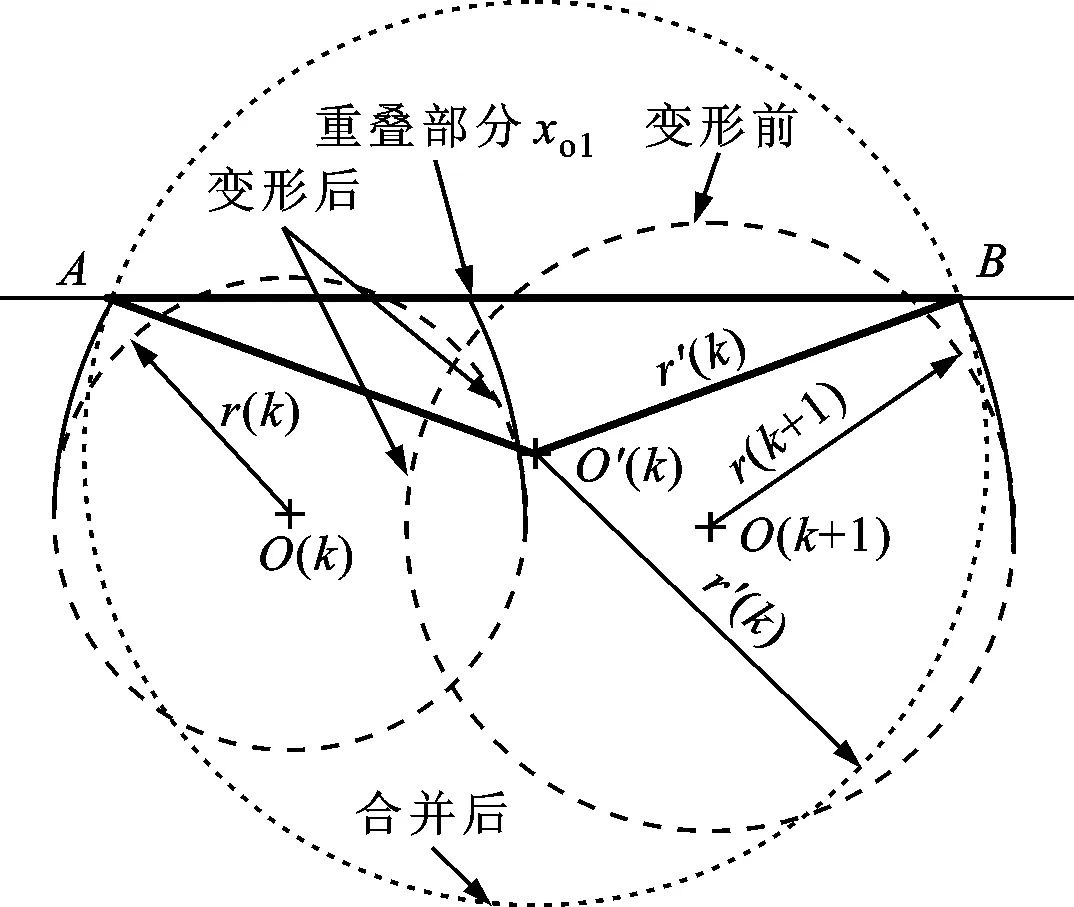
图2　等效粗糙峰及其重叠后合并的示意图

1.4　计算流程

对于二维粗糙表面轮廓,根据GW建模方法[1],将两个粗糙表面的接触视为等效粗糙表面与刚性光滑平面接触,主要的计算步骤如下:

(1)利用“谷-峰-谷”模式的微凸峰确定准则,得到一连续的等效表面轮廓;

(2)在步骤(1)的基础上,刚性平面的位置从等效粗糙表面的最高点开始,取一定的压缩步长,利用1.1节中单个球体的接触理论,计算发生接触微凸体的接触面积、接触力和接触圆半径;

(3)通过步骤(2)中的计算结果,判断相邻微凸体接触半径是否重叠以及单位长度上界面处球体与刚性平面之间的摩擦力是否大于固体表面能,当条件成立时,根据材料守恒原理,将这两个微凸体合并为一个大的微凸体。

具体计算流程如图3所示。

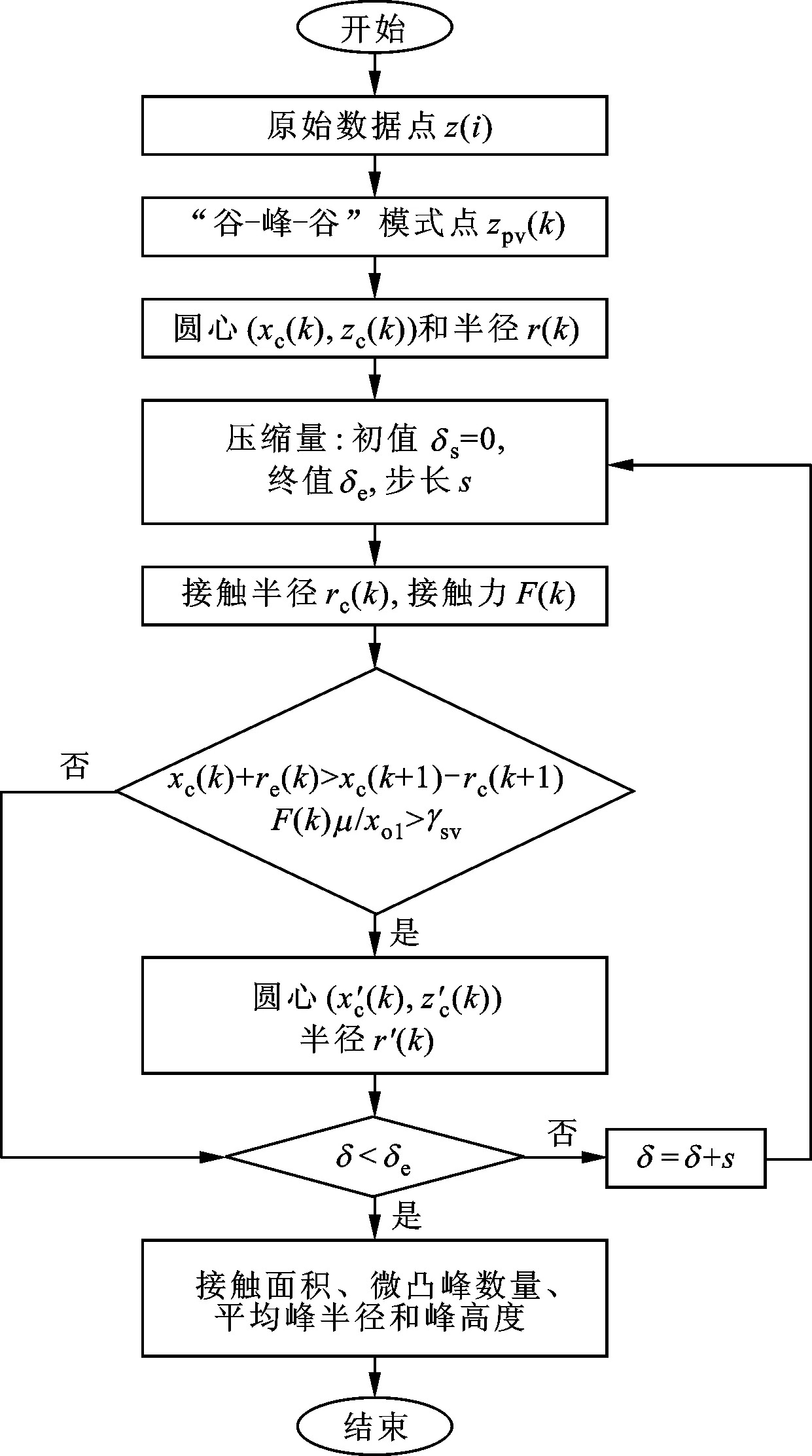
图3　考虑微凸体相互作用的接触特性计算流程

2　结果的比较

为了分析微凸体相互作用对接触面积、微凸峰数量、平均峰半径和峰高度等的影响,采用不同法向变形量、采样间隔和粗糙度等方案,同时与未考虑微凸体相互作用的结果进行对比。

利用文献[12]中金刚砂平板对一铝合金球进行压缩的实验数据如表2所示,取铝合金材料的表面能γsv为77.8 mJ/m2,摩擦系数μ为0.06。

2.1　不同法向变形量的接触特性

在压缩过程中采用表面轮廓4,采样间隔取为0.5 μm,压缩量终值δe为等效粗糙峰中的最大峰值,取60个计算步长。事实上,步长对计算结果也是有影响的,正如在变形过程中总应变不等于各个阶段应变之和一样。通过对比分析,取60和70个步长时的接触面积分别为1.361 6×10-2和1.360 0×10-2mm2,误差已经很小。

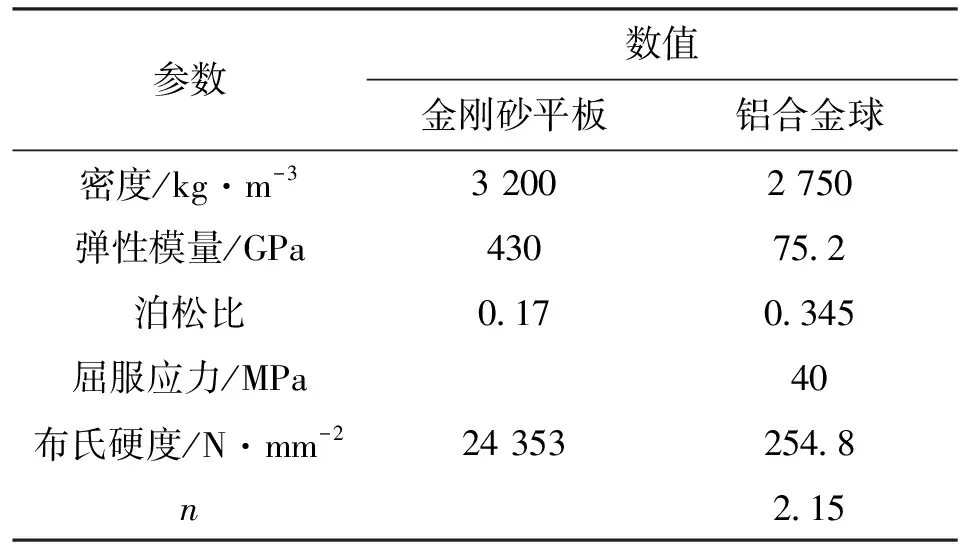
表2　铝合金球压缩实验中测试试件的参数[12]

2.1.1接触面积接触面积与法向参量之间的关系如图4所示。从图4a中可以看出,不论是否考虑微凸体相互作用,接触面积与法向接触力均为线性关系。对于经典的接触理论,如GW[1]、BGT[2]和Persson理论[9],数值仿真分析[7,13-14]以及文献[15]中的实验结果均表明,接触面积与载荷的关系为线性或近似线性。由此可见,本文的分析结果与已有结论是吻合的。

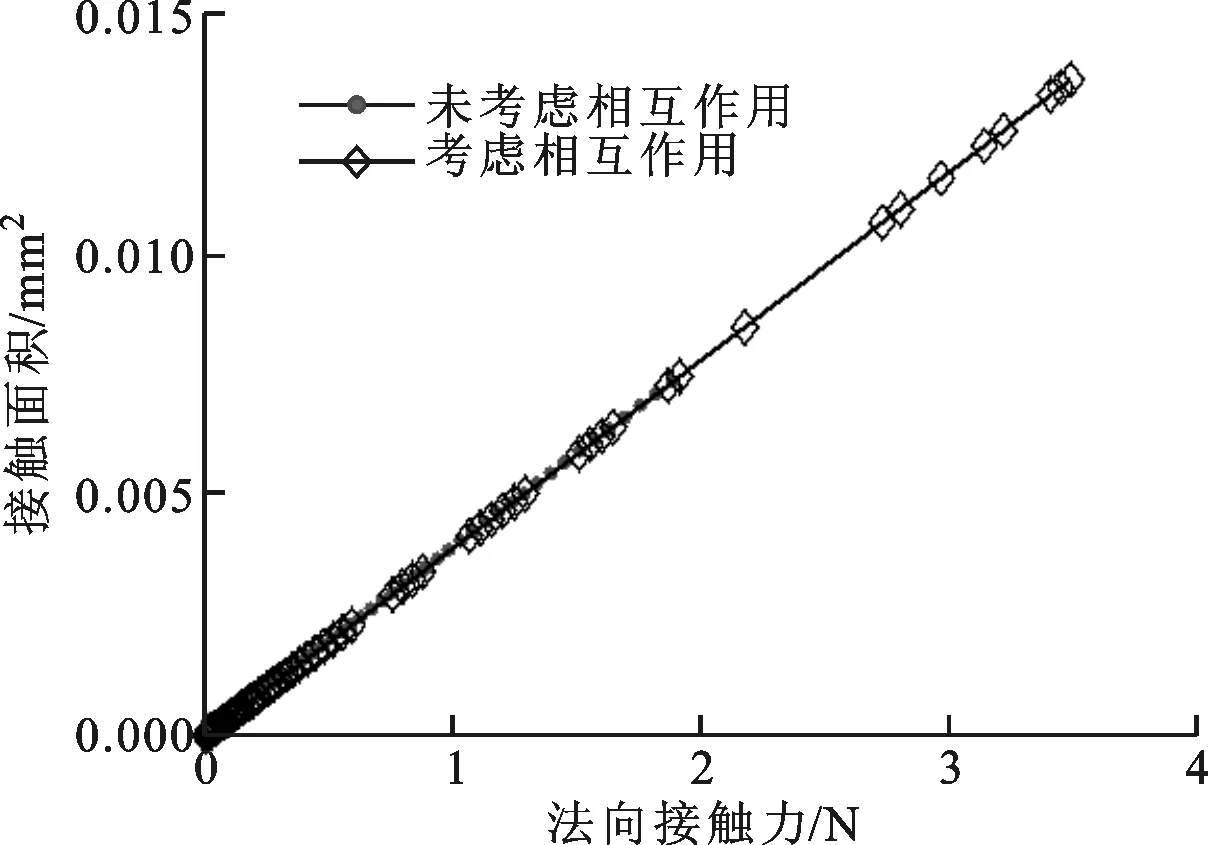
(a)接触面积和法向接触力的关系

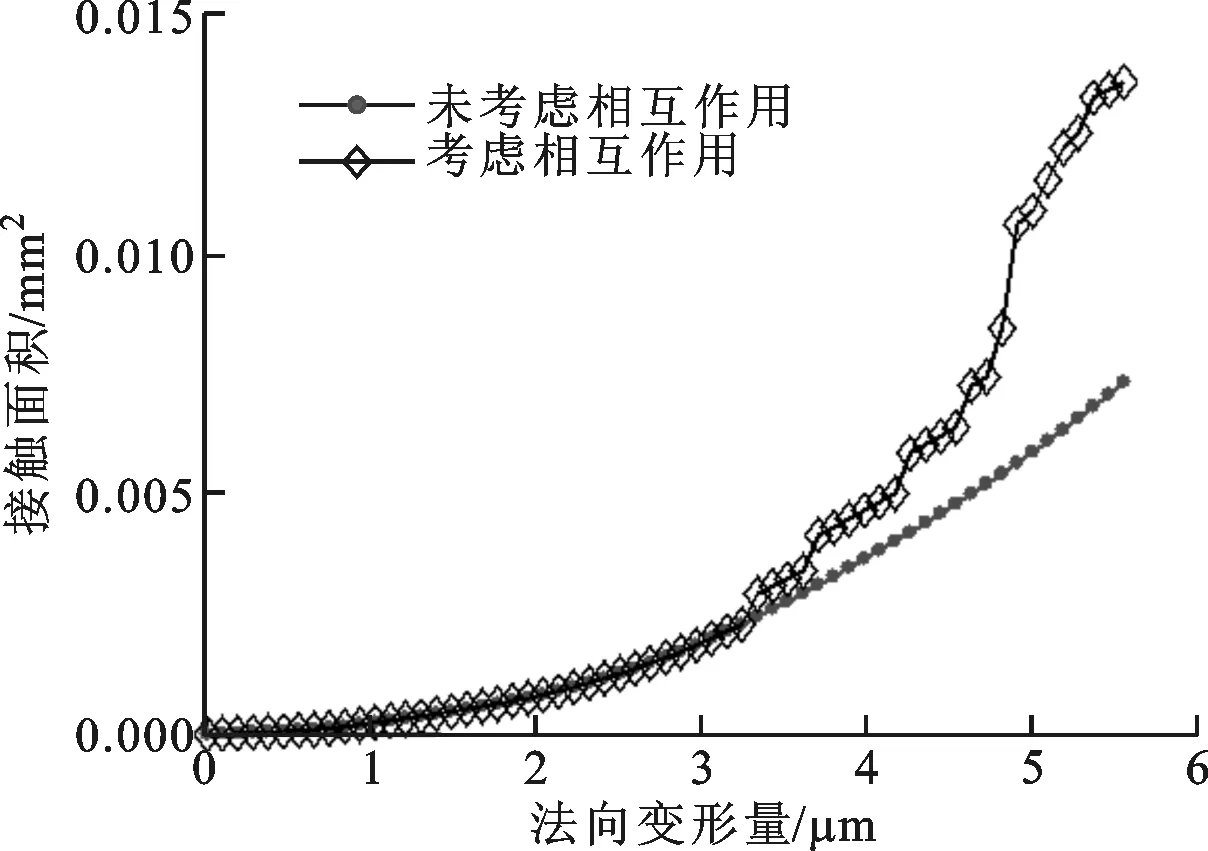
(b)接触面积和法向变形量的关系图4　接触面积与法向参量之间的关系

从图4b中可以看出,粗糙表面的接触面积与法向变形量为类二次幂曲线关系,文献[3]中也有类似的结果,但本文在水平方向上微凸体的合并使接触面积增加,而在文献[3]中发生接触的微凸体使相邻微凸体的原始基准下降,导致接触面积减小。此外,这与单个微凸体的结果还是有所差别的[11]。当存在微凸体相互作用时,曲线并不是光滑的,其主要原因是:①相邻微凸体在满足给定条件时出现合并;②新的微凸体参与接触。当变形量较小时,微凸体相互作用较弱,随着变形量的增加,所造成的影响也变得明显。在工程应用上,影响最大的就是密封问题,通过变形量并不能够真实地反映接触面积的变化,并且随着零件表面积的增大,微凸体相互作用变得更为重要,从实际情况也可以得到,密封一个大的面积显然要比密封一个小的困难得多。

2.1.2微凸峰的接触特性对于特定的微凸峰形状,一个粗糙表面最重要的参数是微凸峰数量、平均峰半径和峰高度。微凸峰接触特性与法向变形量的关系如图5所示。在图5a中,当未考虑微凸体相互作用时,微凸峰数量保持不变,为59个;当考虑相互作用时,峰数量在初始压缩时保持为59个,随着变形量的增加,峰数量逐渐减少,直到最后的38个。在图5b中,未考虑相互作用时,平均峰半径为8.26 μm;考虑相互作用时,平均峰半径的变化与峰数量的变化正好相反,随着法向变形量的增加而变大,最后达到10.01 μm。从图5c可以看出,当存在相互作用时,平均峰高度的变化与峰半径的变化类似,只是在数值上存在差异。

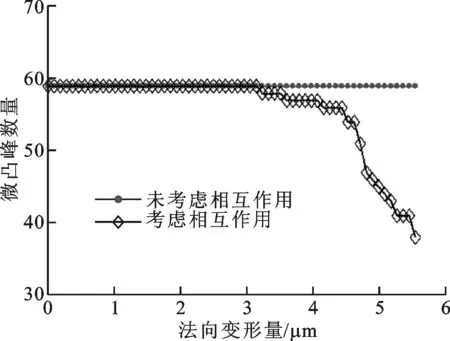
(a)微凸峰数量

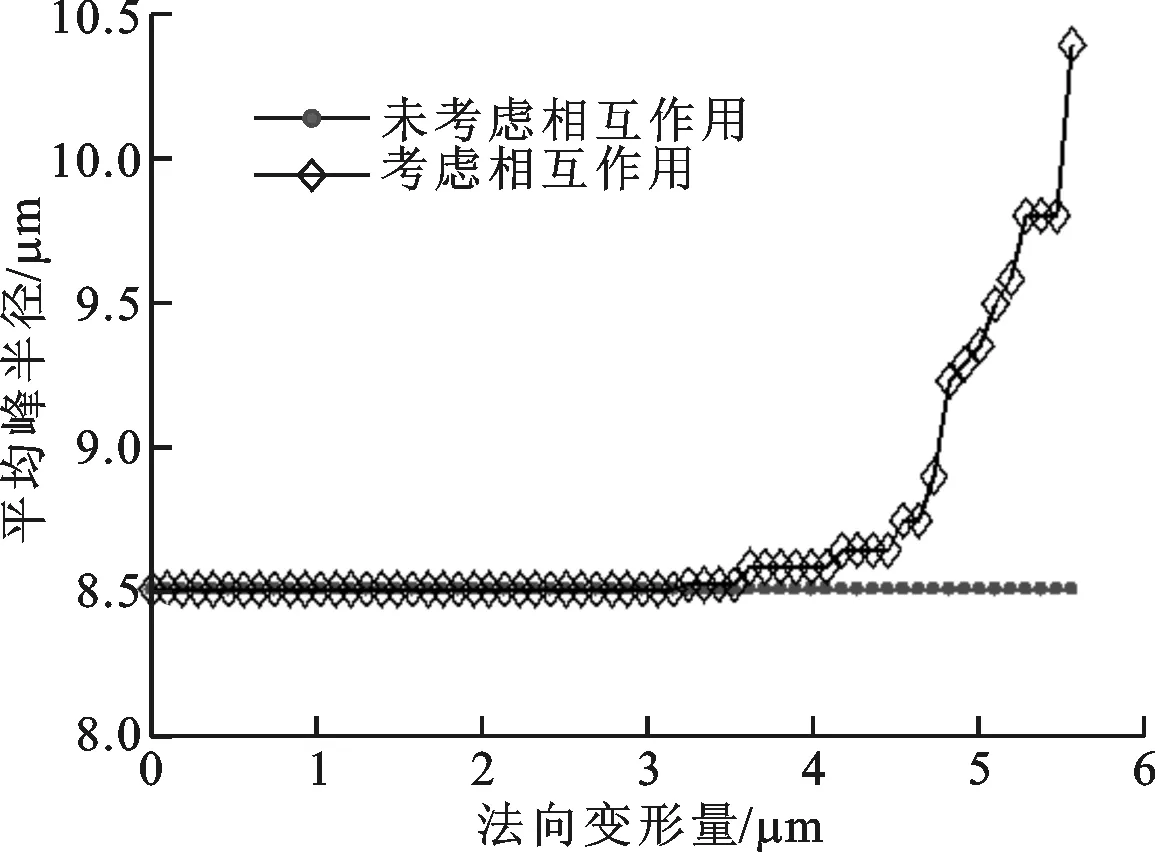
(b)平均峰半径

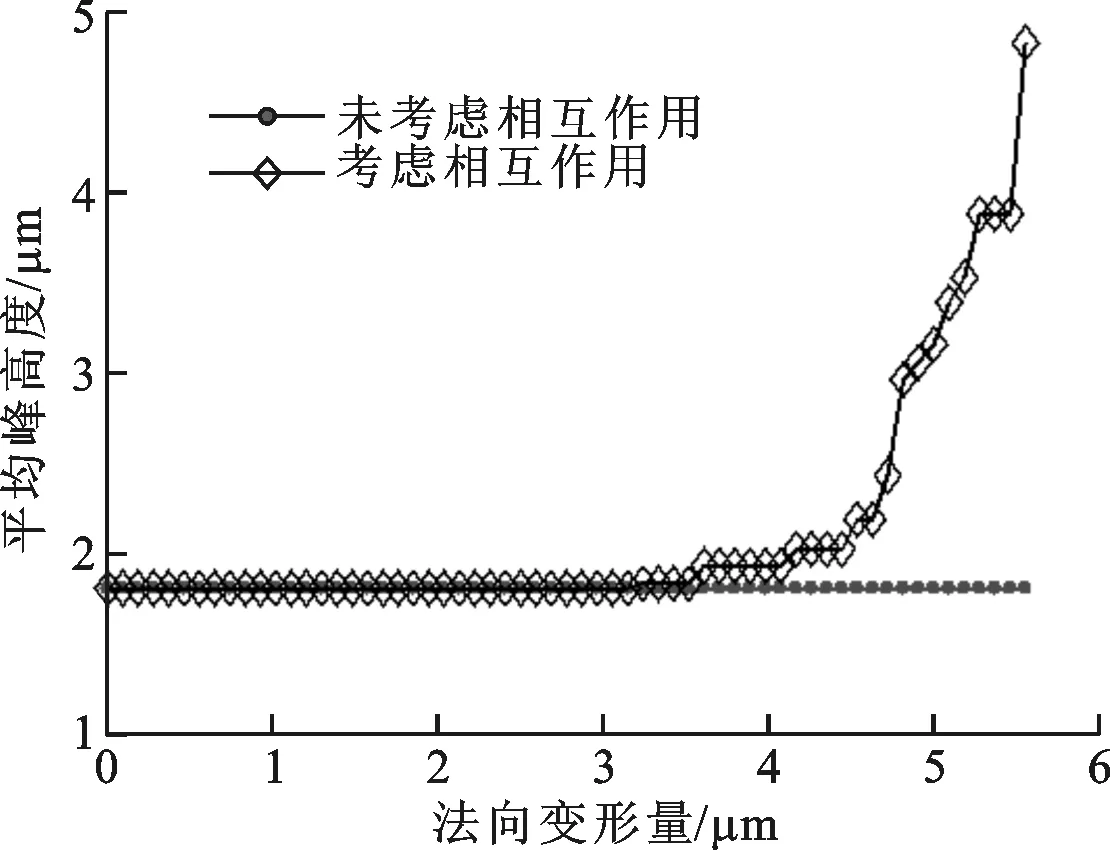
(c)平均峰高度图5　不同法向变形量的微凸峰接触特性

当法向变形量较小时,微凸体相互作用对接触特性的影响不大,相应的参数保持不变。随着变形量增加,相邻微凸体间的作用也逐渐明显,小的微凸体合并为大的,与之相应,粗糙表面上的微凸峰数量减少,峰半径和峰高度变大。考虑一种极端情况,所有的微凸体都发生完全塑性变形,最终的结果将只有一个微凸体,峰半径和峰高度都趋向于无穷大,实现完全光滑平面。

2.2　不同采样间隔的接触特性

下面分析不同采样间隔对接触特性的影响,取法向变形量和计算步长与2.1节的一致,采样间隔分别为0.05、0.1、0.3 μm,并在0.5～5 μm之间每隔0.5 μm进行一次取值。

2.2.1接触面积接触面积随着采样间隔的变化规律如图6所示。接触面积随着采样间隔的减小而变小,中间的波动主要是由于不同的表面形貌信息造成的。对于考虑和未考虑相互作用的两种方式,在较大的采样间隔时,两者是重合的,微凸体间的相互作用不明显。当采样间隔小于3 μm时,相互作用开始变得明显,使接触面积变大,随着采样间隔的进一步减小,在粗糙表面上有更多的微凸体发生相互作用,导致两者之间的差距变得更大。在工程应用上,采用高质量的加工表面往往可以获得更好的密封效果,这主要是因为表面具有更多精细的微观结构,在工作过程中将有更多的微凸体发生相互作用。

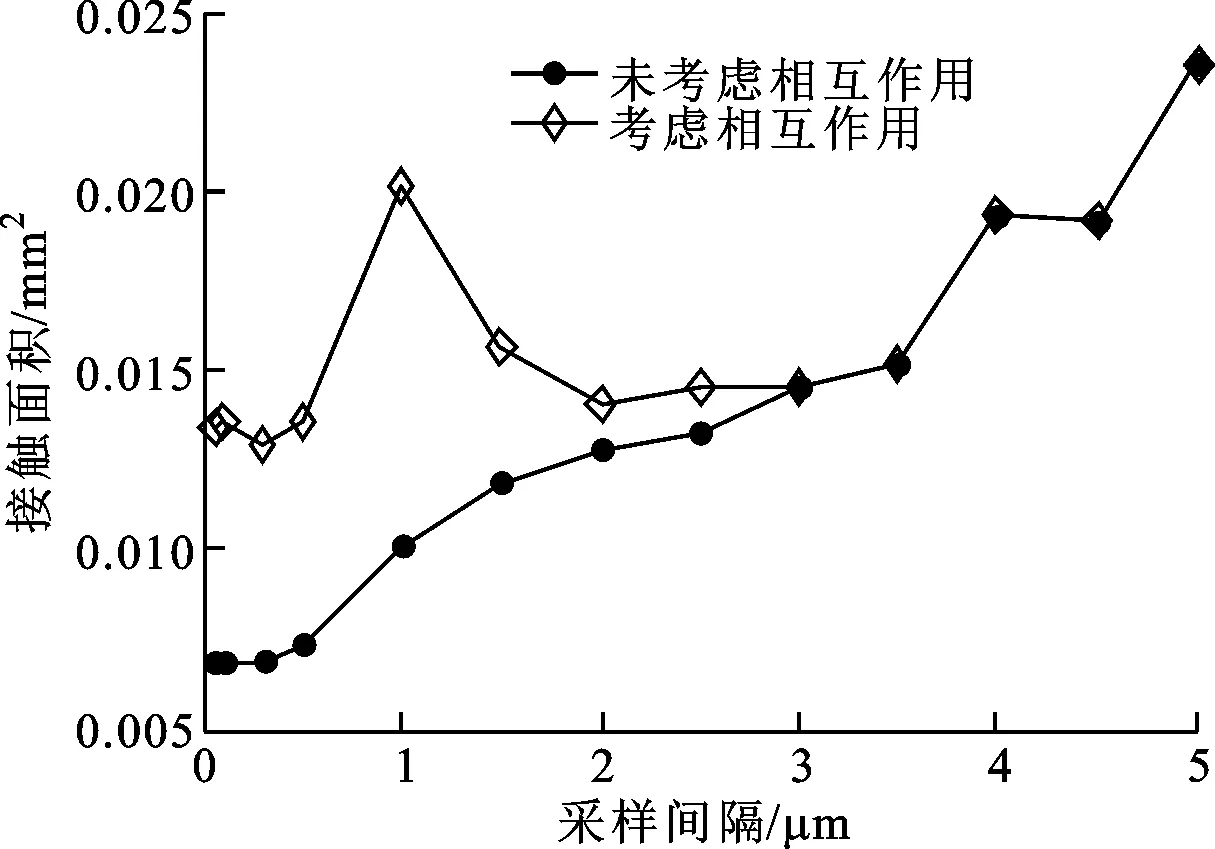
图6　不同采样间隔的接触面积

2.2.2微凸峰的接触特性微凸峰的接触特性随着采样间隔的变化规律如图7所示。

从图7a中可以看出,微凸峰数量随着采样间隔的减小而增多,对于未考虑相互作用的微凸峰数量,从最少的10个增加到最多的65个,这就如同在一定区域内等效球体、晶胞和原子数的变化规律一样[10],而考虑相互作用时,从最少的10个增加到最多的41个。

平均峰半径的变化如图7b所示,随着采样间隔的减小,其变化趋势与峰数量的变化正好相反。当未考虑相互作用时,平均峰半径从最大的94.73 μm逐渐减小到采样间隔为0.05 μm时对应的7.55 μm,而考虑相互作用时,两者的差距从采样间隔为3 μm开始逐渐增加,直到采样间隔为0.05 μm时达到最大,对应的峰半径为9.34 μm。

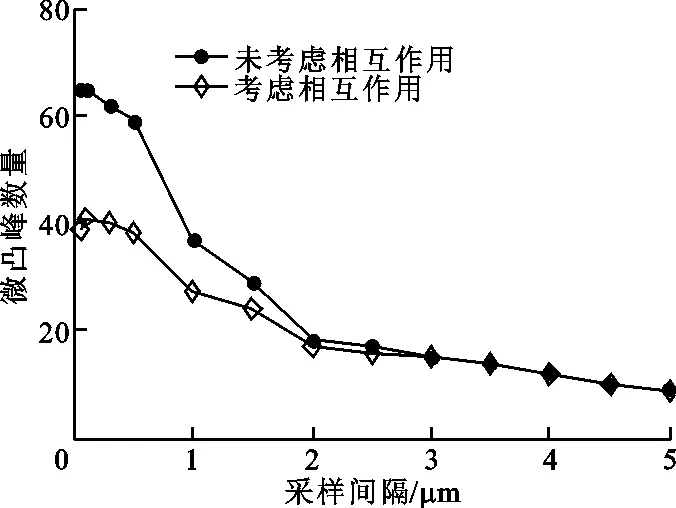
(a)微凸峰数量

(b)平均峰半径

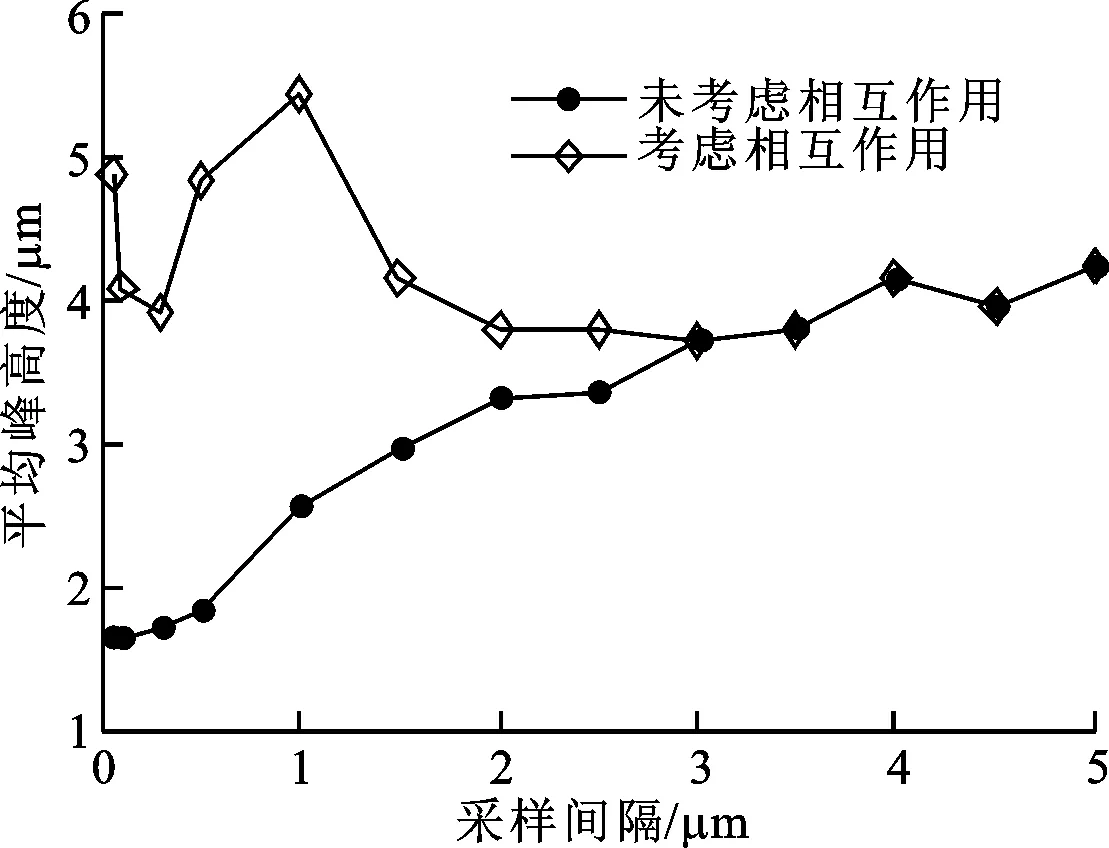
(c)平均峰高度图7　不同采样间隔的微凸峰接触特性

平均峰高度的变化如图7c所示,对于未考虑相互作用的微凸体来说,其变化趋势与平均峰半径的变化类似,随着采样间隔的减小而减小。但是,当考虑相互作用时,同样地,从采样间隔为3 μm开始,微凸峰高度发生明显的变化,与平均峰半径不同的是,当采样间隔大于1.5 μm时,平均峰高度基本上稳定在4 μm,当采样间隔小于1.5 μm时,平均峰高度出现较大的波动,这主要是由于微凸体相互作用造成的,在1 μm处存在一个最大值,为5.41 μm。

当采样间隔减小时,粗糙表面上呈现出更多的微小结构,在外载荷的作用下微凸体间更容易发生相互作用。在分析过程中当相邻微凸体满足给定条件时,将两个较小的微凸体合并为一个大的,这就造成总的微凸峰数量减少,峰半径和峰高度变大,从图7中也可以看出,越能反映粗糙表面上的微观结构,微凸体间的相互作用越明显。

2.3　不同粗糙度的接触特性

2.3.1接触面积为了分析不同粗糙度对接触面积的影响,采用采样间隔为0.5 μm对7个表面轮廓进行分析。接触面积随着粗糙度的变化规律如图8所示。两种作用方式对应的接触面积均随着粗糙度的减小而增大,基本上呈现为两条平行线,这说明微凸体的作用方式与采样间隔有着一定的联系。

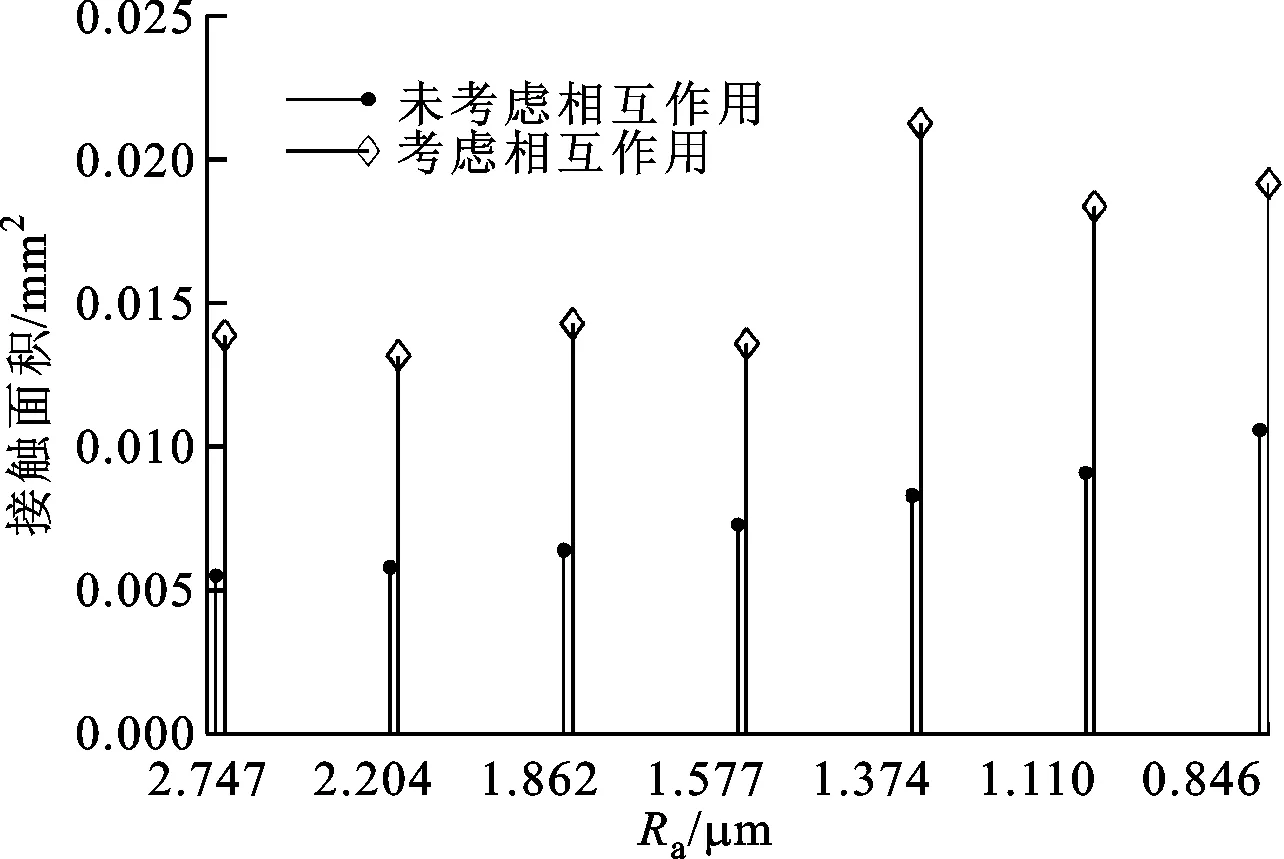
图8　不同粗糙度的接触面积

2.3.2微凸峰的接触特性微凸峰特性与粗糙度之间的关系如图9所示,与文献[10]中的分析结果一致。不同作用方式下的接触特性与法向变形量和采样间隔对应的结果类似。对于微凸峰数量和平均峰半径,均为随着粗糙度的减小而变大,而平均峰高度的变化,与前两者正好相反,并且不同作用方式下的差距在缩小,这主要是因为较小粗糙度的原始峰高度较低。

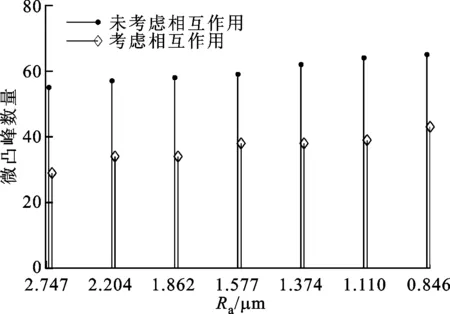
(a)微凸峰数量

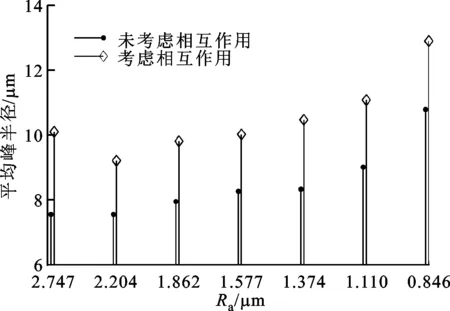
(b)平均峰半径

(c)平均峰高度图9　不同粗糙度的微凸峰接触特性

3　结　论

本文在确定性接触模型的基础上,考虑微凸体间的相互作用,分析了粗糙表面在接触过程中微凸体相互作用对接触特性的影响,得到的主要结论如下。

(1)不论是否考虑微凸体相互作用,接触面积与法向载荷的关系均为线性,这与理论、数值分析以及实验结果是吻合的,验证了本文方法的有效性。

(2)在较小的法向变形量和较大的采样间隔下,微凸体相互作用不明显,接触特性与独立微凸体的一致。

(3)随着法向变形量的增加、采样间隔的减小,不同粗糙度下相互作用的影响变得愈加明显,与未考虑微凸体相互作用的结果相比,微凸峰数量减少,而接触面积、平均峰半径和峰高度增大。

参考文献:

[1]GREENWOOD J A, WILLIAMSON J B P. Contact of nominally flat surfaces [J]. Proceedings of the Royal Society of London, 1966, 295: 300-319.

[2]BUSH A W, GIBSON R D, THOMAS T R. The elastic contact of a rough surface [J]. Wear, 1975, 35(1): 87-111.

[3]CIAVARELLA M, GREENWOOD J A, PAGGI M. Inclusion of “interaction” in the Greenwood and Williamson contact theory [J]. Wear, 2008, 265(5/6): 729-734.

[4]AFFERRANTE L, CARBONE G, DEMELIO G. Interacting and coalescing Hertzian asperities: a new multiasperity contact model [J]. Wear, 2012, 278/279(5): 28-33.

[5]MAJUMDAR A, BHUSHAN B. Fractal model of elastic-plastic contact between rough surfaces [J]. ASME Journal of Tribology, 1991, 113(1): 1-11.

[6]杨楠, 陈大融, 孔宪梅. 多粗糙峰弹塑性接触的有限元分析 [J]. 摩擦学学报, 2000, 20(3): 202-206.

YANG Nan, CHEN Darong, KONG Xianmei. Elastic-plastic finite element analysis of multi-asperity contacts [J]. Tribology, 2000, 20(3): 202-206.

[7]HYUN S, PEI L, MOLINARI J F, et al. Finite-element analysis of contact between elastic self-affine surfaces [J]. Physical: Review EStatistical Nonlinear and Soft Matter Physics, 2004, 70(2): 188-206.

[8]SUN F W, GIESSEN E V, NICOLA L. Interaction between neighboring asperities during flattening: a discrete dislocation plasticity analysis [J]. Mechanics of Materials, 2015, 90: 157-165.

[9]PERSSON B N J. Contact mechanics for randomly rough surfaces: on the validity of the method of reduction of dimensionality [J]. Tribology Letters, 2015, 58(1): 1-4.

[10] 王庆朋, 张力, 杜宝程, 等. 粗糙表面确定性接触模型中峰的再定义 [J]. 西安交通大学学报, 2016, 50(11): 115-120.

WANG Qingpeng, ZHANG Li, DU Baocheng, et al. Re-definition of asperity-peak for deterministic contact model on rough surfaces [J]. Journal of Xi’an Jiaotong University, 2016, 50(11): 115-120.

[11] 王庆朋, 张力, 尚会超, 等. 考虑应变硬化的混合弹塑性接触模型 [J]. 西安交通大学学报, 2016, 50(2): 132-137.

WANG Qingpeng, ZHANG Li, SHANG Huichao, et al. Mixed elastic-plastic contact model considering strain hardening [J]. Journal of Xi’an Jiaotong University, 2016, 50(2): 132-137.

[12] JAMARI J, SCHIPPER D J. Experimental investigation of fully plastic contact of a sphere against a hard flat [J]. ASME Journal of Tribology, 2006, 128: 230-235.

[13] CARBONE G, BOTTIGLIONE F. Asperity contact theories: do they predict linearity between contact area and load [J]. Journal of the Mechanics and Physics Solids, 2008, 56(8): 2555-2572.

[14] PAGGI M, CIAVARELLA M. The coefficient of proportionalityκbetween real contact area and load with new asperity models [J]. Wear, 2010, 268(7/8): 1020-1029.

[15] 张斌, 徐锦芬, 高志, 等. 摩擦过程中真实接触面积的灰色分析 [J]. 摩擦学学报, 1996, 16(1): 61-69.

ZHANG Bin, XU Jinfen, GAO Zhi, et al. Grey model analysis on real contact area during friction process [J]. Tribology, 1996, 16(1): 6169.