倾斜式双滚柱包络环面蜗杆传动弹流润滑分析

李金宽, 柳在鑫, 李世蓉, 朱焱

(1.西华大学机械工程学院, 610039, 成都; 2.电子科技大学成都学院电子工程系, 611731, 成都)

在机械传动机构中,绝对光滑的表面是不存在的。如果接触表面的粗糙度远小于润滑油膜厚度,可将接触表面假设为光滑表面[1]。弹流润滑油膜的厚度常常只有几微米甚至小于1微米,与蜗杆传动副的磨削加工工艺形成的表面粗糙度[2]处于同一数量级,在这种情况下接触表面的粗糙度不能忽略。

Simon等对一种新型的圆柱蜗杆传动进行了润滑特性研究,并分析了传动副的承载能力、功率损耗[3]。Sharif等运用弹流润滑理论并计入齿面弹性变形与润滑油的黏压效应,对渐开线蜗杆传动的润滑问题进行了研究[4-5]。张有忱等采用杨沛然-温诗铸经验公式对平面二次包络环面蜗杆传动和圆弧圆柱蜗杆传动进行了油膜厚度计算与分析[6-7]。刘绪仁等利用伽辽金法和八节点等参元离散雷诺方程,对ZC2型蜗杆传动进行了全膜等温弹流润滑分析[8]。王进戈等根据虎克润滑状态简图中各润滑状态区域内的油膜厚度公式,对滚锥包络环面蜗杆传动进行了润滑状态的研究[9]。邱昕洋等利用杨沛然、温诗铸回归出的线接触Ree-Eyring流体热弹流润滑的膜厚公式,计算得到了钢制平面蜗轮传动的油膜厚度分布规律,揭示了传动副的润滑状态[10]。杨捷等根据Dowson-Higgison经验公式,对无侧隙平面一次包络端面啮合环面蜗杆进行了油膜厚度求解[11]。李金宽等利用牛顿迭代法和牛顿-拉夫逊法对倾斜式双圆柱滚子包络环面蜗杆传动进行了数值求解,得到了传动副的油膜压力和油膜厚度曲线,并通过与经验公式解进行比较,验证了数值解的正确性[12]。

上述对蜗杆传动弹流润滑问题所进行的研究没有考虑粗糙度的影响。为了更直观地研究该传动副在考虑粗糙度时的弹流润滑问题,本文基于弹性流体动力润滑理论和牛顿流体润滑特性,对倾斜式双滚柱包络环面蜗杆传动的线接触问题进行了求解,得到了该传动副在粗糙峰和粗糙谷时的油膜厚度和油膜压力,并进行了分析,以期为该传动副的后续研究工作提供理论依据。

1　传动副啮合模型

倾斜式双滚柱包络环面蜗杆传动(如图1所示)是一种新型的活动齿蜗轮蜗杆传动装置[13-14],蜗轮由活动蜗轮和固定蜗轮组成,滚柱均匀分布在固定蜗轮和活动蜗轮的周向,滚柱轴线与蜗轮径向倾斜一定角度(即图1中的γ,称为滚柱倾斜角),利用滚柱代替传统蜗轮轮齿,此时蜗轮轮齿可以绕自身轴线转动,将传动副之间的滑动摩擦变为滚动摩擦,而环面蜗杆则是以轴承的外缘柱面为原始母面一次包络形成。就单排滚柱而言,工作过程中存在楔形的侧隙,从而保证了传动的正常工作和良好的润滑,对整体而言,通过采用双排滚柱错位布置,消除了传动的回程误差,使传动平稳,提高了传动精度[13-14]。

图1　倾斜式双滚柱包络环面蜗杆传动示意图

传动副在传动过程中为瞬时多齿啮合,接触线是复杂的空间曲线,且每一个啮合齿对上仅有一条接触线。在啮合传动过程中,该传动副的当量曲率半径[12]

R=1/kσ

(1)

式中:kσ为诱导法曲率,可根据文献[13]求得。

基于两纯滚动接触进行弹流润滑分析,根据文献[10]所提供的方法,求得该传动副的卷吸速度

vjx=(vw+vg)/2

(2)

式中:vw、vg分别为蜗轮和蜗杆在啮合点处沿接触线法线方向的速度,可根据文献[12]求得。

每个齿对在啮合点处单位长度上的载荷

(3)

式中:i=1,2,3,4;Ki为齿间载荷分配系数[15];Fn为接触点处的法向载荷;L为接触线长度;Ft为接触点处的圆周力;αn为压力角;β为螺旋升角[14];T1为输入转矩;d1为蜗杆分度圆直径。

倾斜式双滚柱包络环面蜗杆传动的当量曲率半径R、卷吸速度vjx和单位长度上的载荷w从啮入到啮出的变化曲线如图2所示,图中φ2为蜗轮转角。由图2可以看到:从啮入到啮出,当量曲率半径逐渐增大,卷吸速度先减小后增大,单位长度上的载荷先增大后减小;在蜗杆喉部附近卷吸速度达到最小值,单位长度上的载荷达到最大值。

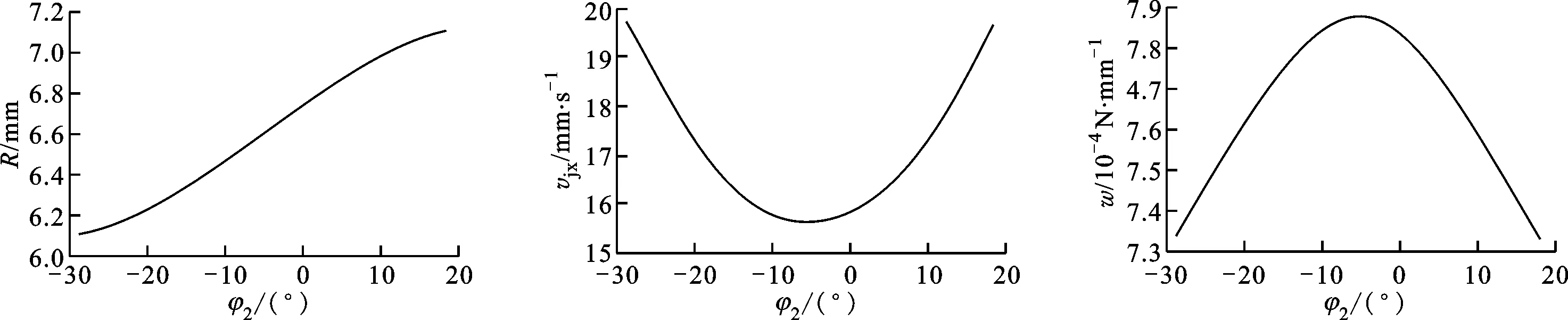
(a)当量曲率半径 (b)卷吸速度 (c)单位长度上的载荷图2　啮入啮出过程中当量曲率半径、卷吸速度和单位长度上载荷的变化曲线

2　粗糙齿面弹流润滑模型及数值解法

根据弹性流体动力润滑理论[16],并结合倾斜式双滚柱包络环面蜗杆传动的传动特点,传动副蜗杆齿面与蜗轮齿面(即滚柱面)之间的线接触可以简化为一当量圆柱体与一平面的接触[12],如图3所示。

图3　线接触简化模型

2.1　线接触弹流润滑的基本方程

为了方便求解计算,需对弹流润滑数学模型进行归一化[12,16]

X=x/b;H=h/R;W=w/E′R;U=η0vjx/E′R

P=p/pH;η*=η/η0;ρ*=ρ/ρ0

式中:E′为综合弹性模量[12];h为油膜厚度;w为单位长度上的载荷;η0为初始黏度;x为流动方向;b为赫兹接触半宽;p为油膜压力;pH为最大赫兹接触压力;ρ0为初始密度。

根据牛顿流体弹流润滑模型,等温线接触弹流润滑的基本方程及量纲一方程如下。

(1)雷诺方程及其归一化方程[12,16]分别为

(4)

(5)

式中

边界条件为

(2)根据文献[17],采用接触中点存在一个单峰粗糙度的情况,即有

s(x)=δ(|x|-1)2

(6)

式中:δ为单峰粗糙度的幅值。考虑共轭齿面粗糙度的影响,线接触油膜厚度方程[17]为

h(x)=

(7)

其量纲一方程为

H(x)=

(8)

式中:H0为量纲一刚体中心膜厚;S(X)为量纲一表面粗糙度函数

S(X)=δ(|X|-1)2

(9)

黏压方程、密压方程、载荷平衡方程的量纲一方程[16,18]如下

η*=exp{(lnη0+9.67)[(1+5.1×10-9p)z-1]}

(10)

式中:z=α/[5.1×10-9(lnη0+9.667)],α为黏压系数。

(11)

(12)

2.2　弹流润滑的数值解法

根据倾斜式双滚柱包络环面蜗杆传动的传动特点,采用牛顿迭代法对该传动副的线接触等温弹流润滑问题进行求解,即利用差分法将积分形式的雷诺方程离散,求得各节点压力、中心膜厚和油膜终点位置(或终点处膜厚)的非线性方程组,然后用牛顿-拉夫逊法进行求解[12,18]。数值计算流程图如图4所示。

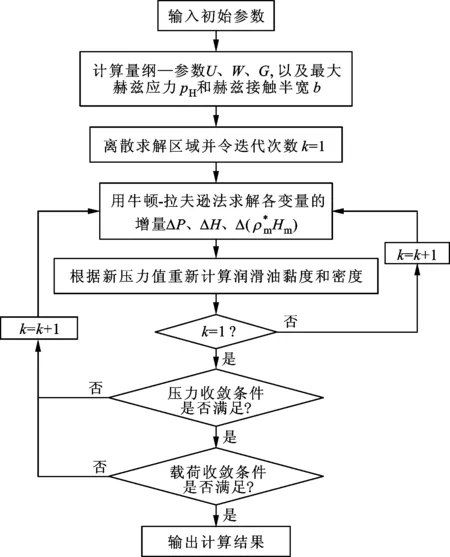
图4　线接触弹流润滑数值计算流程图

(1)雷诺离散方程为

(13)

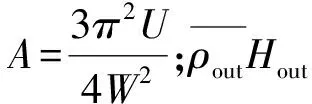
(2)膜厚离散方程为

(14)

式中:Kij为变形影响系数[12]。

(3)载荷离散方程为

(15)

3　数值结果及分析

倾斜式双滚柱包络环面蜗杆传动的共轭齿面粗糙度单粗糙峰和单粗糙谷的模型如图5所示。

(a)粗糙峰 (b)粗糙谷图5　单粗糙峰和单粗糙谷

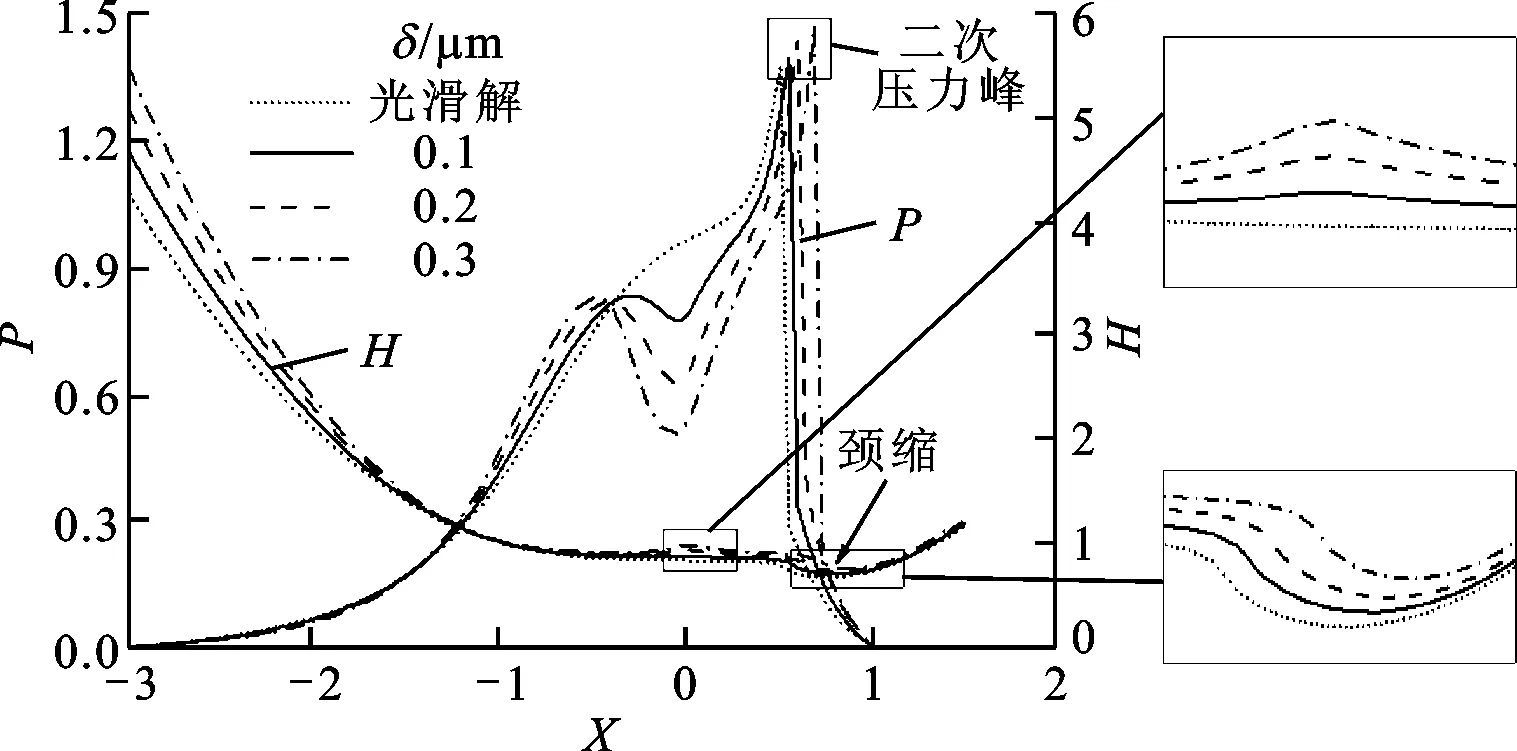
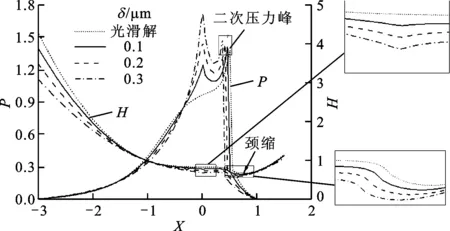
取量纲一计算范围为X=[Xin,Xout]=[-3,1.5],输入功率P=5 kW,输入转速n1=1 450 r/min,蜗杆和蜗轮的材料参数μ1=μ2=0.3,E1=E2=210 GPa。以右旋蜗杆传动为例,当Z1=1、Z2=25、A=125 mm、R=6.5 mm、c2=7 mm、k=0.4、α=1°、γ=6°时,传动副的弹流润滑特性如图6所示,其中图6a为单粗糙谷时幅值对该传动副弹流润滑特性的影响,图6b为单粗糙峰时幅值对该传动副弹流润滑特性的影响。

由图6可知,在主要承载区域,由于单峰粗糙度的存在,使得油膜压力在粗糙作用区域内凸起和凹陷,在油膜压力凸起和凹陷的区域引起油膜厚度轻微凹陷和凸起,但凹陷和凸起的时刻略有滞后,且油膜厚度凹陷和凸起的幅值很小,这是因为在弹流油膜压力的作用下油膜厚度的变化滞后,引起了上述现象的发生。

(a)单粗糙谷幅值的影响

(b)单粗糙峰幅值的影响图6　不同粗糙度幅值下的弹流润滑特性

对于单粗糙谷而言,在共轭齿面单粗糙谷的作用区域,随着单粗糙谷幅值的增大油膜压力凹陷的幅度变大,二次压力峰值也随单粗糙谷幅值的增大而增大,且向出口区方向移动。在弹流润滑的入口区域和共轭齿面单粗糙谷的作用区域,单粗糙谷幅值对弹流润滑油膜厚度的影响较大,油膜厚度随单粗糙谷幅值的增大而增大;在出口区域单粗糙谷幅值对油膜厚度影响较小。单粗糙谷幅值越大,弹流润滑油膜的颈缩现象就越延迟。

对于单粗糙峰而言,在共轭齿面单粗糙谷的作用区域,随着单粗糙峰幅值的增大油膜压力凸起的幅度增大,二次压力峰值也随单粗糙峰幅值的增大而增大,且向入口区方向移动。在弹流润滑的入口区域和共轭齿面单粗糙峰的作用区域,单粗糙峰幅值对弹流润滑油膜厚度的影响较大,油膜厚度随粗糙度幅值的增大而减小;在出口区域,单粗糙峰幅值对油膜厚度没有太大影响。单粗糙峰幅值越大,弹流润滑油膜颈缩现象就越提前。

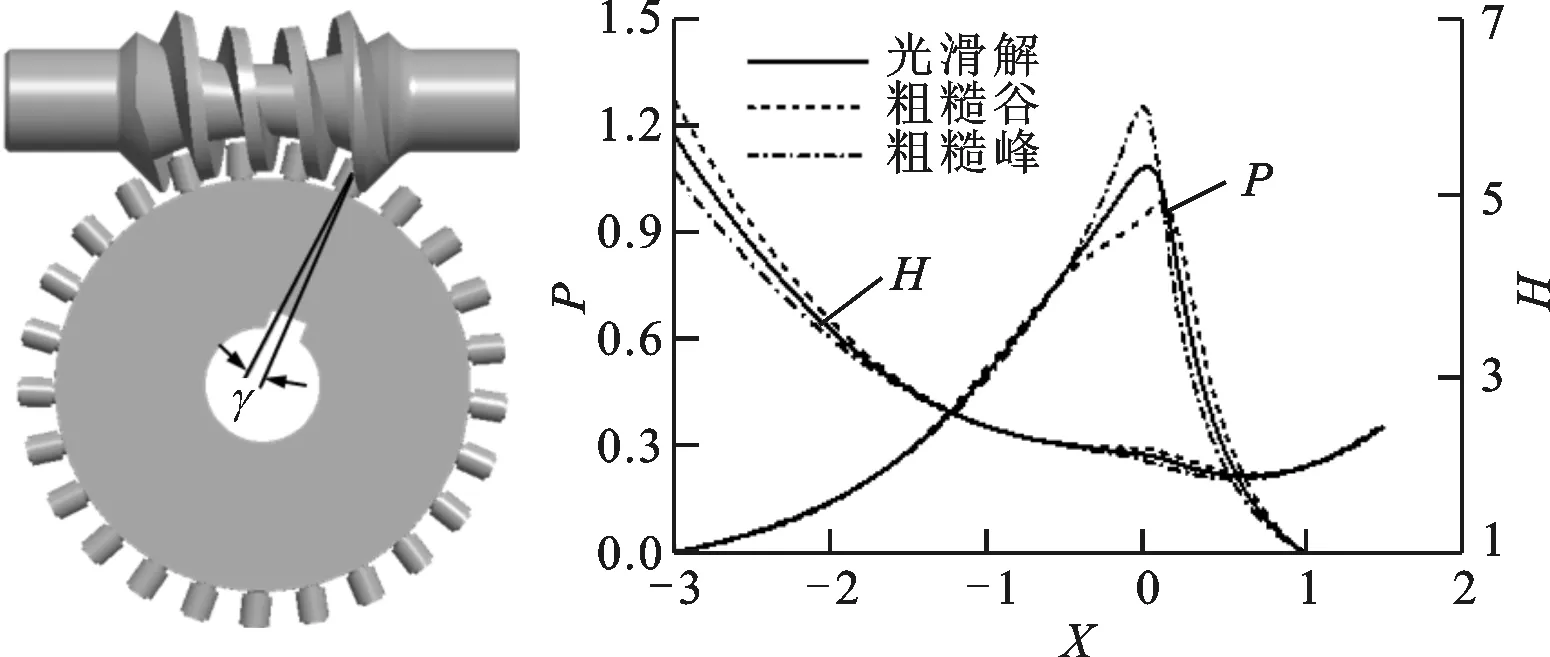
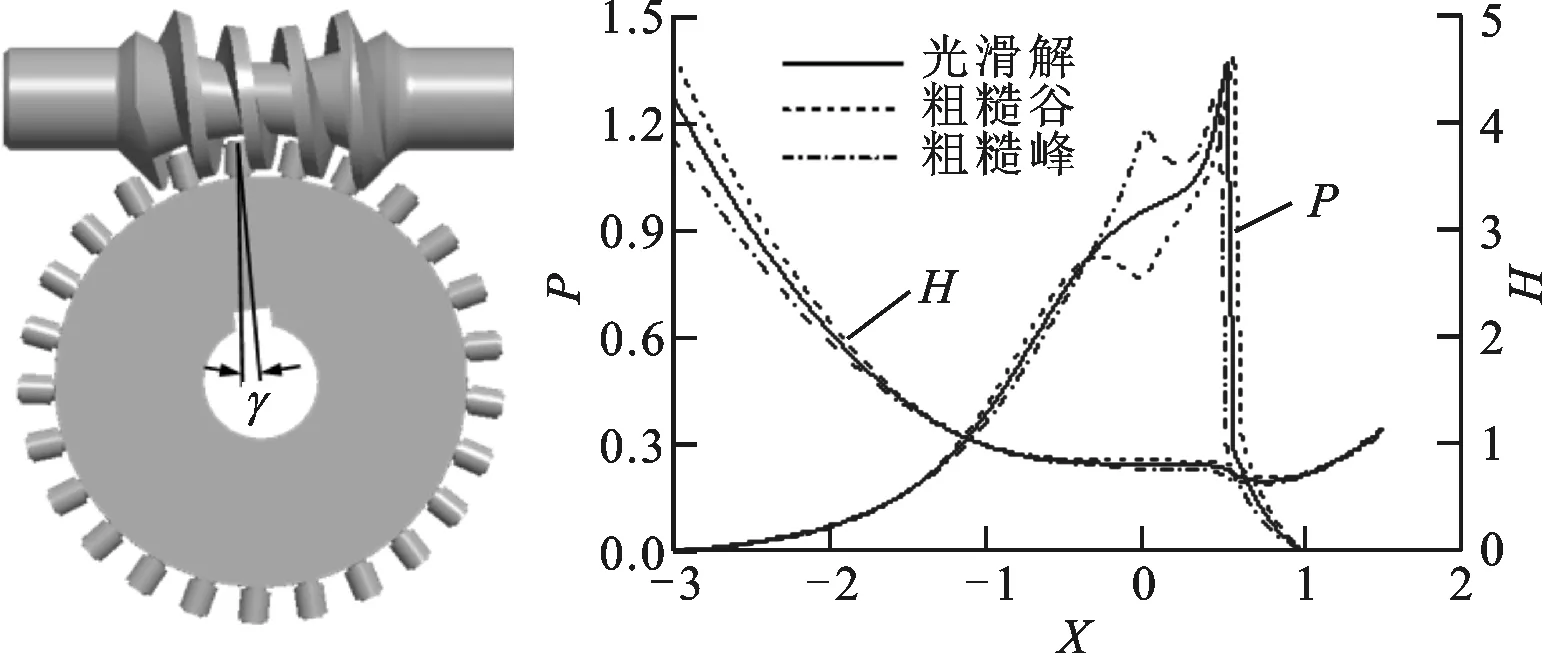
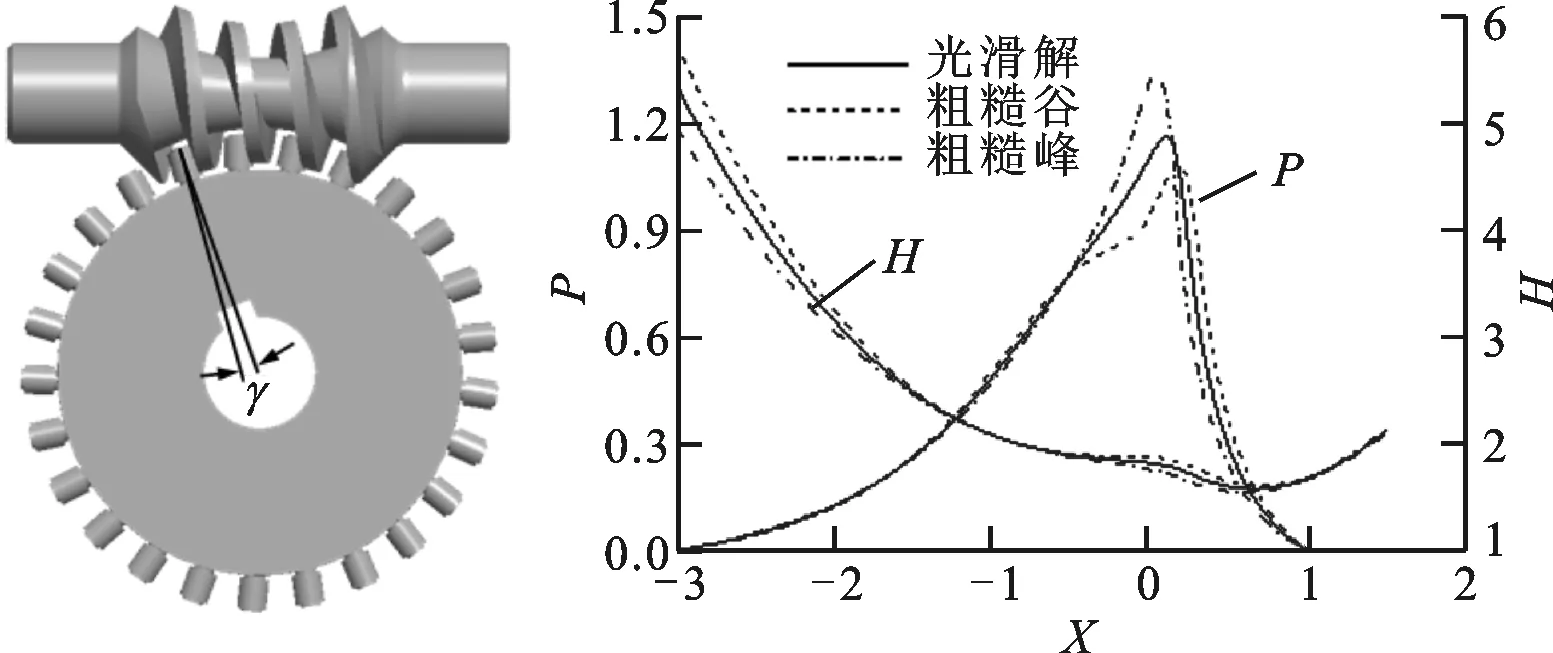
以粗糙度幅值为0.1 μm为例,倾斜式双滚柱包络环面蜗杆传动在4个不同啮合时刻的油膜压力和油膜厚度分布如图7所示。

从图7中可以看出:从啮入到啮出,光滑解的弹流润滑油膜二次压力峰值先增大后减小,油膜厚度先减小后增大;在粗糙峰和粗糙谷的作用区域,粗糙峰引起的油膜压力峰值最大,光滑解的次之,粗糙谷的最小;在弹流求解的入口区以及粗糙峰和粗糙谷的作用区域,粗糙谷的油膜厚度最大,光滑解的次之,粗糙峰的最小,在弹流求解的入口区表现得尤为突出。

在单粗糙谷和单粗糙峰的承载区的每个啮合时刻,单粗糙谷和单粗糙峰对弹流润滑油膜压力的影响较大,对油膜厚度的影响相对较小,这是由于单粗糙谷或单粗糙峰引起的弹流润滑油膜压力峰反过来作用于单粗糙谷或单粗糙峰,使得单粗糙谷和单粗糙峰的幅值减小,油膜不容易刺穿。

在第3个齿开始啮合的时刻,油膜二次压力峰值最大,油膜厚度达到最小值,由此可以判断出,第3个齿开始啮合的时刻即为润滑油膜最危险的时刻,此时共轭齿面间容易发生胶合失效。

(a)第1个齿开始啮合时

(b)第2个齿开始啮合时

(c)第3个齿开始啮合时

(d)第4个齿开始啮合时图7　不同啮合时刻的弹流润滑特性

在第2个齿和第3个齿开始啮合的时刻,单粗糙峰、单粗糙谷处的油膜压力出现了明显的凸起和凹陷。在第2个齿开始啮入和第3个齿开始啮入的时刻,无论是单粗糙峰还是单粗糙谷均在粗糙度的作用时刻产生了2个油膜压力峰值,这是由于单粗糙谷和单粗糙峰的存在使弹流润滑的承载区分为粗糙承载区和光滑承载区,单粗糙谷或单粗糙峰内的油膜承受的压力相对于光滑承载区较小,而油膜压力集中由单粗糙谷或单粗糙峰外面的光滑承载区承受,从而造成了弹流油膜的双压力峰现象。

当设计参数滚柱半径、滚柱偏距和喉径系数取不同值,其他参数不变时,该传动副在三齿啮合时刻设计参数对油膜压力和油膜厚度的影响如图8～图10所示。

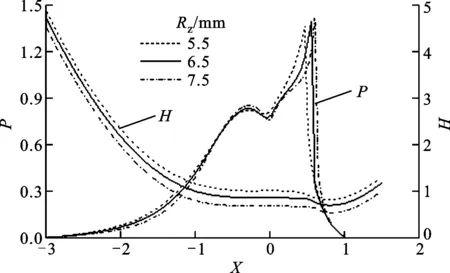
(a)粗糙谷时的影响

(b)粗糙峰时的影响图8　滚柱半径对弹流润滑特性的影响

从图8中可以看出:随着滚柱半径Rz的增大,单粗糙谷时作用承载区的油膜压力谷值减小,其位置不发生变化,二次压力峰值增大且向出口区方向移动;单粗糙峰时作用承载区的油膜压力峰值减小,其位置无变化,但是二次压力峰值明显减小且向出口区移动。无论是单粗糙谷还是单粗糙峰时,油膜厚度均减小,颈缩现象延迟出现。

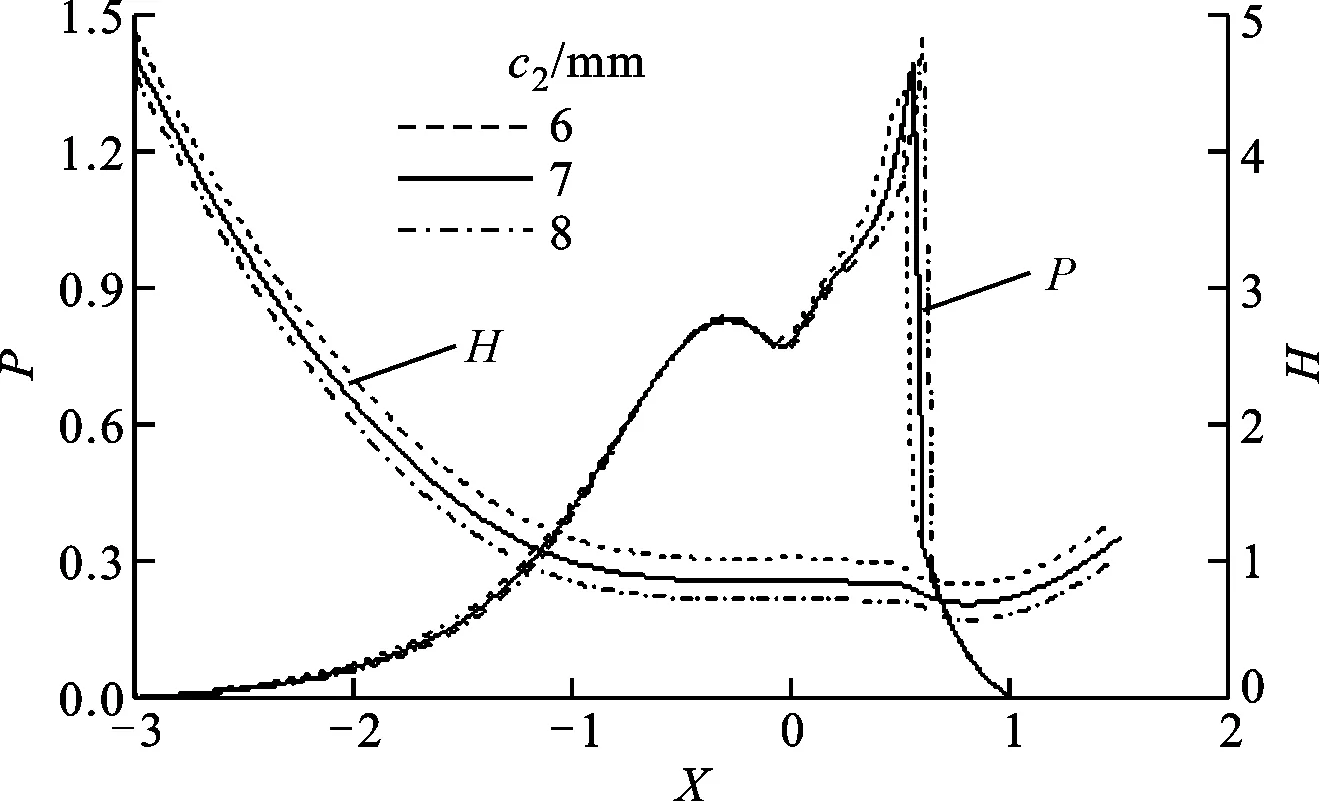
(a)粗糙谷时的影响

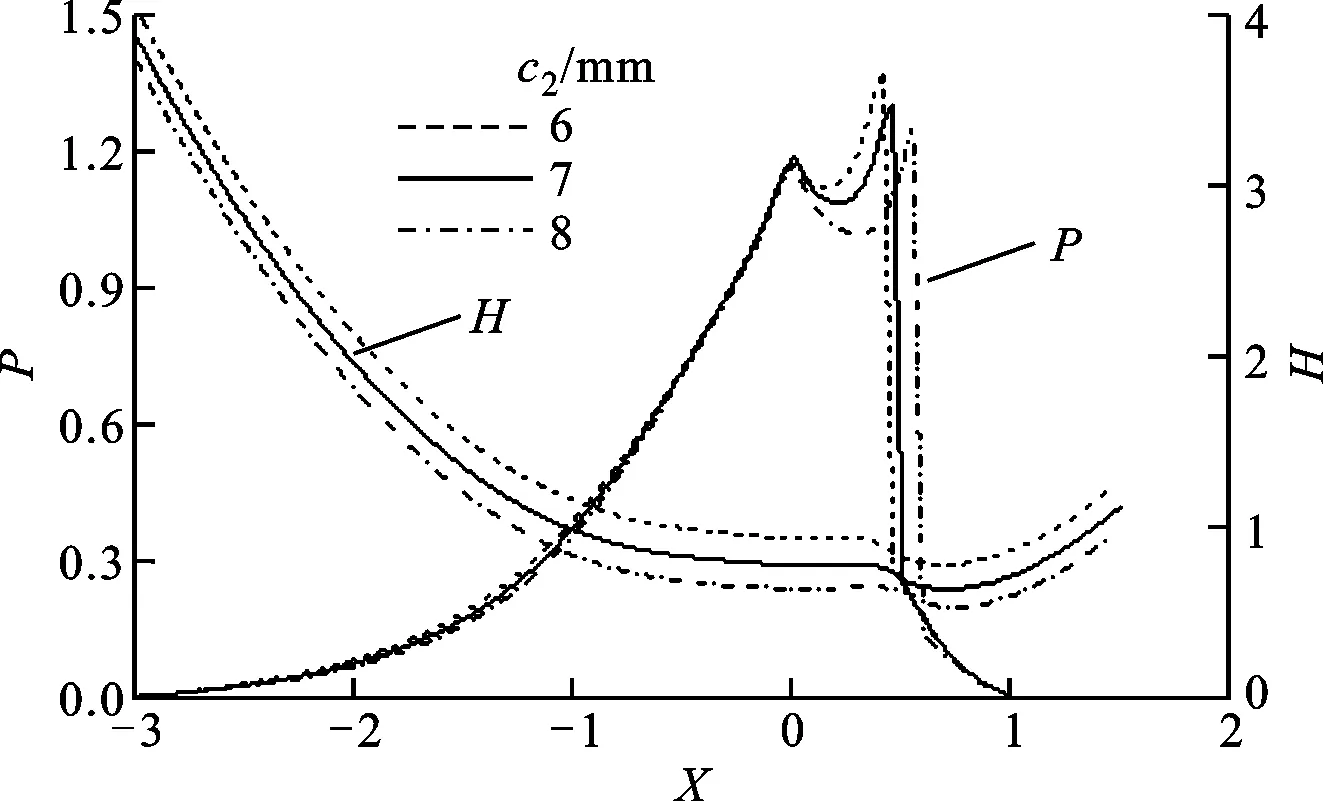
(b)粗糙峰时的影响图9　滚柱偏距对弹流润滑特性的影响

从图9中可以看出:随滚柱偏距c2的增大,单粗糙谷时作用承载区的油膜压力减小,其位置不发生变化,二次压力峰值增大且远离入口区;单粗糙峰时作用承载区的油膜压力值略有增大,二次压力峰值减小且向出口区移动。无论是单粗糙谷还是单粗糙峰时,油膜厚度均随c2的增大而减小,颈缩现象延迟出现。

从图10中可以看出:随喉径系数k的增大,单粗糙谷时作用承载区的油膜压力减小,二次压力峰值也呈减小趋势且向出口区移动;单粗糙峰时作用承载区的油膜压力随k的变化不大,但二次压力峰值增大且向入口区移动。无论是单粗糙谷还是单粗糙峰时,油膜厚度均减小,颈缩现象延迟出现。

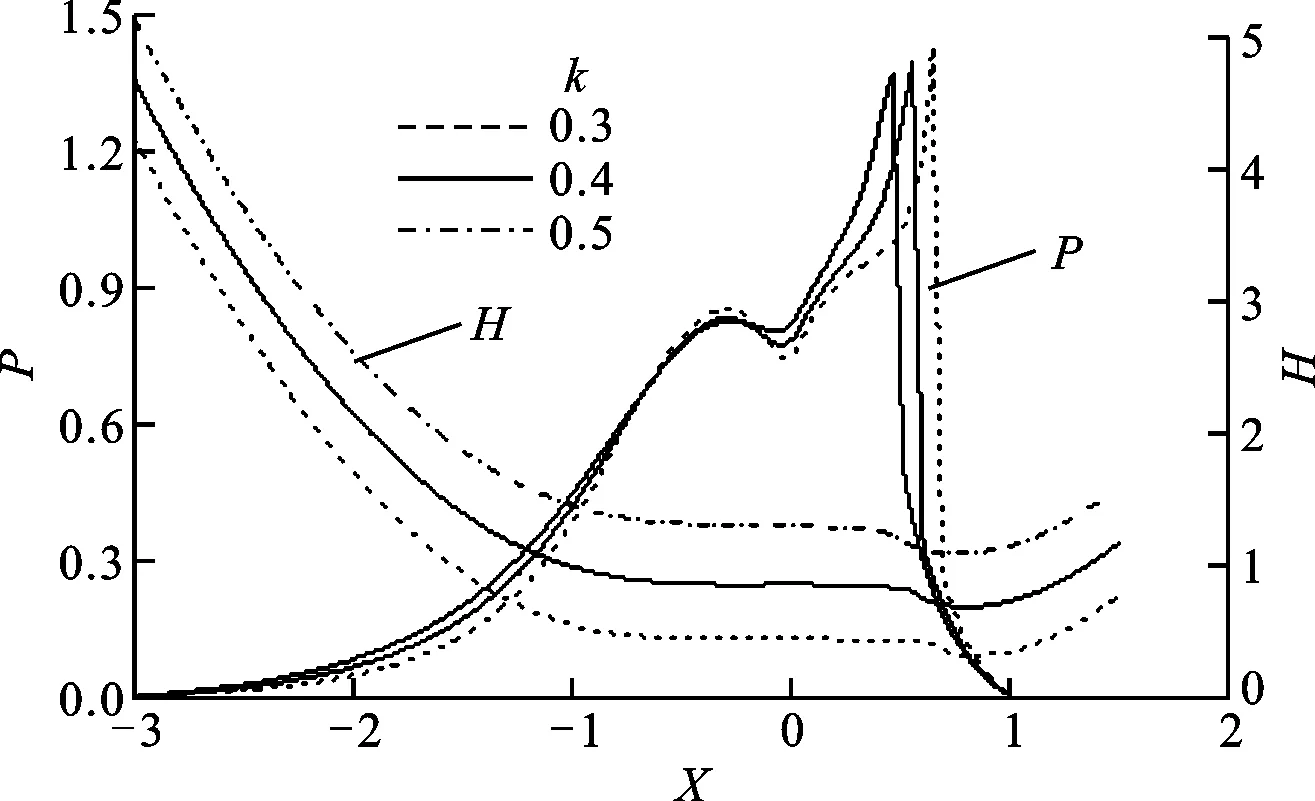
(a)粗糙谷时的影响

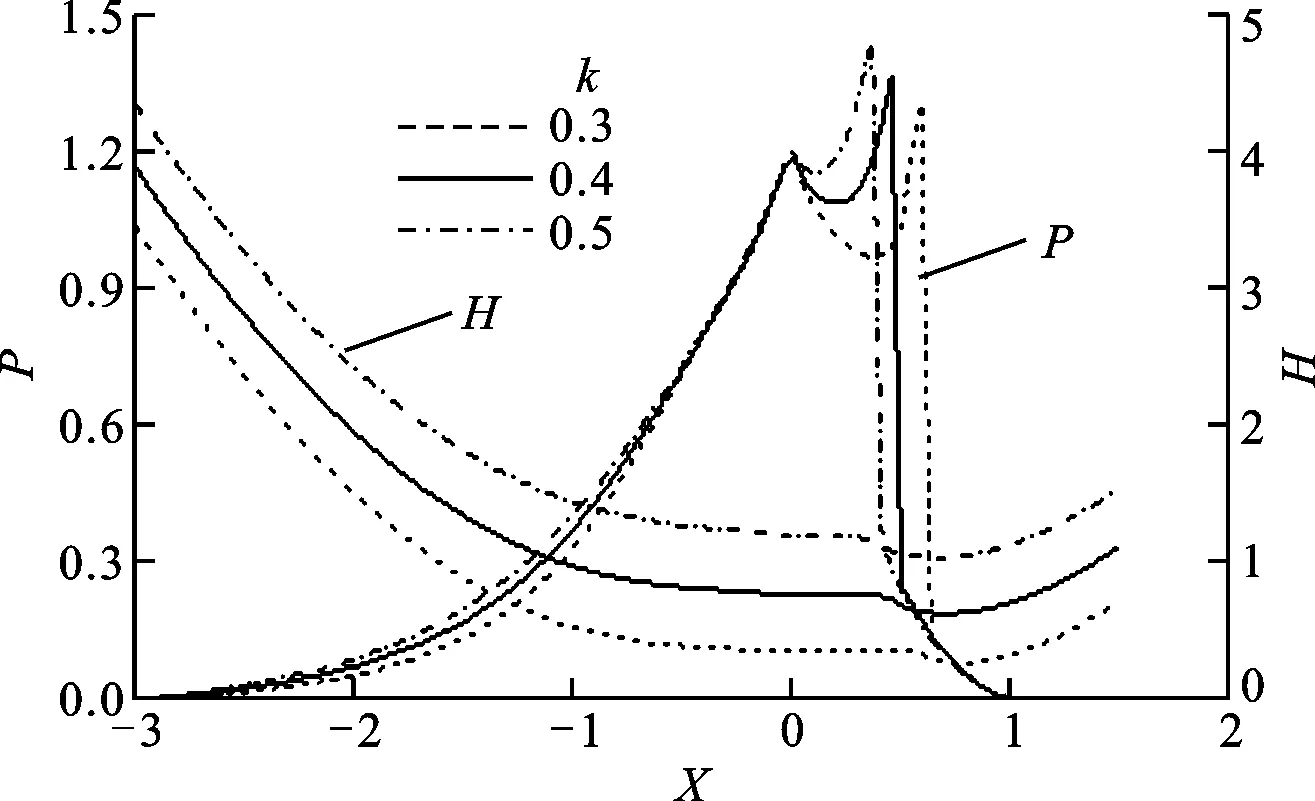
(b)粗糙峰时的影响图10　喉径系数对弹流润滑特性的影响

4　结　论

本文以倾斜式双圆柱滚子包络环面蜗杆传动为例,以考虑传动副共轭接触表面粗糙度为出发点,在作者前期研究的基础上,建立了单峰粗糙度时的传动副等温弹流润滑数学模型,对该新型传动副的弹流润滑问题进行了计算求解,得到传动副在不同啮合时刻的弹流润滑特性,获得的主要结论如下:

(1)在主要承载区域,单个粗糙峰使油膜压力凸起,形成一个局部高压,此高压可以在一定程度上把粗糙峰压入表面,使油膜不易被刺穿,从而减轻单个粗糙峰带来的不良影响,防止润滑失效的危险,而单个粗糙谷的存在会使粗糙谷作用处的油膜压力降低,导致粗糙谷作用处两侧光滑区的油膜压力产生双压力峰,容易刺穿油膜,存在润滑失效的危险;

(2)在第3个齿开始啮入的时刻,油膜压力峰值最大,粗糙度将会造成油膜厚度减小变薄,形成润滑的危险区;

(3)滚柱半径和滚柱偏距过大或喉径系数过小都不利于传动副动压油膜的形成,对传动副的润滑不利;

(4)通过提高传动副的加工精度来减小粗糙度幅值,可以有效提高传动副的弹流承载能力。

参考文献:

[1]王优强, 卞荣. 连续波状粗糙度对直齿轮热弹流润滑的影响 [J]. 机械工程学报, 2009, 45(8): 112-118.

WANG Youqiang, BIAN Rong. Influence of surface roughness wave on thermal elastohydrodynamic lubrication of involute spur gears [J]. Journal of Mechanical Engineering, 2009, 45(8): 112-118.

[2]CHEN Yonghong, ZHANG Guanghui, CHEN Bingkui, et al. A novel enveloping worm pair via employing the conjugating planar internal gear as counterpart [J]. Mechanism and Machine Theory, 2013, 67: 17-31.

[3]SIMON V. EHD lubrication characteristics of a new type of ground cylindrical worm gearing [J]. Journal of Mechanical Design, 1997, 119(1): 101-107.

[4]SHARIF K J, KONG S, EVANS H P, et al. Contact and elastohydrodynamic analysis of worm gears: part 1 Theoretical formulation [J]. Proceedings of the Institution of Mechanical Engineers: Part CJournal of Mechanical Engineering Science, 2001, 215(7): 817-830.

[5]SHARIF K J, KONG S, EVANS H P, et al. Contact and elastohydrodynamic analysis of worm gears: part 2 Results [J]. Proceedings of the Institution of Mechanical Engineers: Part CJournal of Mechanical Engineering Science, 2001, 215(7): 831-846.

[6]张有忱, 孟惠荣, 张立仁. 蜗杆传动的弹流润滑研究 [J]. 机械设计, 1999(10): 24-25.

ZHANG Youchen, MENG Huirong, ZHANG Liren. Analysis of elastohydrodynamic lubrication of worm drive [J]. Journal of Machine Design, 1999(10): 24-25.

[7]张有忱, 康凯, 张立仁. 圆弧圆柱蜗杆传动弹流润滑分析 [J]. 北京化工大学学报, 2001, 28(2): 52-55.

ZHANG Youchen, KANG Kai, ZHANG Liren. Analysis of the elastohydrodynamic lubrication of arc cylindrical worm drive [J]. Journal of Beijing University of Chemical Technology, 2001, 28(2): 52-55.

[8]刘绪仁, 安兆达. 有限元法在蜗杆传动弹流润滑中的应用 [J]. 哈尔滨工业大学学报, 1990, 22(6): 94-96.

LIU Xuren, AN Zhaoda. An application of the finite element method in EHL of worm drive [J]. Journal of Harbin Institute of Technology, 1990, 22(6): 94-96.

[9]王进戈, 张均富, 王强. 滚锥包络环面蜗杆传动的润滑状态分析 [J]. 哈尔滨工业大学学报, 2005, 37(7): 940-942.

WANG Jinge, ZHANG Junfu, WANG Qiang. Lubrication states analyses on rolling cone enveloping hourglass worm gearing [J]. Journal of Harbin Institute of Technology, 2005, 37(7): 940-942.

[10] 邱昕洋, 张光辉, 秦大同. 钢制平面蜗轮传动弹流润滑分析 [J]. 重庆大学学报, 2010, 33(3): 24-29.

QIU Xinyang, ZHANG Guanghui, QIN Datong. Analysis of elastohydrodynamic lubrication of steel planar wormgear drive [J]. Journal of Chongqing University, 2010, 33(3): 24-29.

[11] 杨捷, 王进戈, 陈守安, 等. 无侧隙平面一次包络端面啮合环面蜗杆副弹流润滑分析 [J]. 西安交通大学学报, 2017, 51(3): 87-91.

YANG Jie, WANG Jinge, CHEN Shouan, et al. Analysis on elastohydrodynamic lubrication of the planar enveloped toroidal worm in anti-backlash endface meshing [J]. Journal of Xi’an Jiaotong University, 2017, 51(3): 87-91.

[12] 李金宽, 柳在鑫, 张翠. 倾斜式双圆柱滚子包络环面蜗杆传动的等温弹流润滑分析 [J]. 西安交通大学学报, 2017, 51(5): 88-94.

LI Jinkuan, LIU Zaixin, ZHANG Cui. Analysis on isothermal elastohydrodynamic lubrication performance of inclined double-roller enveloping hourglass worm drive [J]. Journal of Xi’an Jiaotong University, 2017, 51(5): 88-94.

[13] 柳在鑫, 王进戈, 张均富, 等. 交错轴双滚子包络环面蜗杆传动啮合分析 [J]. 四川大学学报(工程科学版), 2012, 44(4): 221-225.

LIU Zaixin, WANG Jinge, ZHANG Junfu, et al. Meshing analysis of non-parallel double-roller enveloping hourglass worm gearing [J]. Journal of Sichuan University (Engineering Science Edition), 2012, 44(4): 221-225.

[14] 柳在鑫, 王进戈, 张均富. 倾斜式双圆柱滚子包络环面蜗杆传动几何特性分析 [J]. 北京理工大学学报, 2013, 33(5): 459-464.

LIU Zaixin, WANG Jinge, ZHANG Junfu. Geometrical characteristics analysis of non-parallel double-roller enveloping hourglass worm gearing [J]. Transactions of Beijing Institute of Technology, 2013, 33(5): 459-464.

[15] 柳在鑫, 王进戈, 张均富, 等. 倾斜式双滚子包络环面蜗杆副承载能力研究 [J]. 高技术通讯, 2013, 23(5): 491-496.

LIU Zaixin, WANG Jinge, ZHANG Junfu, et al. Research on the load carrying capacity of inclined double-roller enveloping hourglass worm gears [J]. Chinese High Technology Letters, 2013, 23(5): 491-496.

[16] 温诗铸, 杨沛然. 弹性流体动力润滑 [M]. 北京: 清华大学出版社, 1992, 13-16, 63-111.

[17] HUANG P, WEN S Z. Sectional micro-elasto-hydrodynamic lubrication [J]. ASME Journal of Tribology, 1993, 115(1): 148-151.

[18] 黄平. 润滑数值计算方法 [M]. 北京: 高等教育出版社, 2012: 151-154.

[本刊相关文献链接]

董国忠,张辉,李月,等.混合弹流润滑系统的建模与摩擦学特性研究.2018,52(1):107-114.[doi:10.7652/xjtuxb201801 016]

孟凡净,刘焜,秦涛.颗粒流润滑力链演变及动力学状态的研究.2017,51(9):106-111.[doi:10.7652/xjtuxb201709015]

李金宽,柳在鑫,张翠.倾斜式双圆柱滚子包络环面蜗杆传动的等温弹流润滑分析.2017,51(5):88-94.[doi:10.7652/xjtuxb201705013

张东亚,高峰,王建磊,等.仿生含油叠层复合材料的高温摩擦学性能.2017,51(5):69-74.[doi:10.7652/xjtuxb201705 011]

杨捷,王进戈,陈守安,等.无侧隙平面一次包络端面啮合环面蜗杆副弹流润滑分析.2017,51(3):87-91.[doi:10.7652/xjtuxb201703015]

张平,张小栋,董晓妮,等.滑动轴承润滑油膜厚度光纤动态精密检测模型.2016,50(5):45-50.[doi:10.7652/xjtuxb 201605007]

雷默涵,姜歌东,梅雪松,等.高速球轴承微接触弹流摩擦及生热分析.2016,50(4):81-88.[doi:10.7652/xjtuxb201604 013]

蒲伟,王家序,杨荣松,等.重载下准双曲面齿轮传动界面润滑机理分析.2015,49(11):55-61.[doi:10.7652/xjtuxb2015 11010]

许聪,李猛,景敏卿,等.超声法测量圆柱滚子轴承润滑油膜厚度.2015,49(10):61-66.[doi:10.7652/xjtuxb201510010]

褚坤明,王家序,蒲伟,等.混合润滑状态下滤波减速器的啮合冲击分析与修形方法.2015,49(7):140-148.[doi:10.7652/xjtuxb201507023]

吴建华,雷源,王刚,等.往复式冰箱压缩机曲轴动态特性与轴承润滑计算分析.2015,49(2):55-61.[doi:10.7652/xjtuxb201502010]

蒲伟,王家序,周广武,等.卷吸速度方向与椭圆短轴成一夹角的弹流润滑渐近网格加密算法.2014,48(9):95-100.[doi:10.7652/xjtuxb201409016]

尹必峰,钱晏强,卢振涛,等.缸套表面复合织构润滑性能理论及试验研究.2014,48(9):74-80.[doi:10.7652/xjtuxb 201409013]

耿涛,孟庆丰,贾谦,等.薄衬层结构滑动轴承润滑膜厚度的超声检测方法.2014,48(8):80-85.[doi:10.7652/xjtuxb 201408014]

翟强,朱永生,闫柯,等.高速角接触轴承油气润滑两相流动特性数值研究.2014,48(6):86-90.[doi:10.7652/xjtuxb 201406015]