Concurrent topology optimization for minimization of total mass considering load-carrying capabilities and thermal insulation simultaneously

Kai Long·Xuan Wang·Xianguang Gu

1 Introduction

Structural topology optimization is intended to place the given material to achieve best structural performance.The pioneer work can be traced to Bendsøe and Kikuchi[1],the topology optimization has developed in a variety of directions with the emergence of substantial approaches including homogenization method,solid isotropic material with penalization(SIMP)method[2,3],evolutionary structural optimization method[4]and bi-directional evolutionary structural optimization(BESO)method[5],level set method[6–8]and phase field method[9].With the aim of establishing a direct link between topology optimization and a computer aided design(CAD)modeling system,more recently,an explicit topology optimization approach based on a moving morphable components(MMC)concept was presented by Guo et al.[10–15].Compared with the traditional method,the MMC method can render the solution containing more geometry and mechanical information in optimized topology.Comprehensive reviews on a specific method or comparison of various methods and their applications are given in Refs.[16–18].Meanwhile,topology optimization with inverse homogenization technique was proposed initially in microstructural design of porous and composite materials[19,20].The increasing advancement of additive manufacturing technology makes it possible to fabricate various man-made materials,such as porous material with negative Poisson’s ratio over large deformations[21],orthotropic material for negative or zero compressibility[22].The state of-the-art for material design via topology optimization can be referenced in Ref.[23].

To date,the mentioned research is confined to individual macrostructural optimization or micro-scale material optimization,i.e.designing the macrostructures composed of optional materials or designing the microstructures for the expected or extreme properties individually.Concurrent design of structure and material becomes one of the hardest tasks in the fields of structural engineering and materials engineering,which has attracted the attention of many researchers.Rodrigues et al.[24]firstly addressed a hierarchical optimization formulation for optimizing material distribution in both macrostructure and microstructure.Later,this hierarchical approach was extended to 3D elastic structures by Coelho et al.[25].In their methods,optimal microstructures may vary from point to point,which leads to high computational cost and manufacture difficulties.To address these problems,Liu et al.[26]suggested a concurrent computational procedure that the porous material is uniform and periodically distributed in macrostructure.The extension of this approach for maximum primary frequency and minimum compliance of thermo-elastic structures was given by Niu et al.[27]and Deng et al.[28]successively.Then Guo et al.[29]presented a robust concurrent optimization formulation emphasized on uncertainties of loads.Optimized topologies of microstructure tend to be isotropic and Kagome structure under such uncertainties.The work of Huang et al.[30]used the BESO method for realizing the concurrent optimization design with the unambiguous configurations on both macro-and micro-scales.Nowadays,the BESO algorithm has been developed to achieve multifunctional designs[31]and to maximize natural frequency with a given mass[32].Also,Xu et al.[33–35]furthered the BESO method to concurrent topology optimization in regard to material distribution in macrostructure and periodic microstructure under harmonic,transient,and random excitations.Zhang and Sun[36]revealed the size effect of materials and structures in the integrated two-scale optimization approach.More recently,Xia and Breitkopf[37,38]proposed an FE2resolution framework focused on nonlinearity for the concurrent design.The study by Jia et al.[39]presented a hierarchical design of structures and multiphase material cells.Furthermore,Long et al.[40]introduced a two-scale topology optimization method for maximizing the frequency of macrostructure that are composed of periodic composite units consisting of two isotropic materials with distinct Poisson’s ratios.The work of Chen et al.[41]presents concurrent design method based on the moving is o-surface threshold concept.

Volume or mass fraction of macrostructure or/and microstructure is taken as the constraint to improve general convergence in above concurrent optimization studies.As indicated by Sigmund and Maute[18],the volume constraint is regarded as the basic constraint for the academic interest.However,most real life applications have to meet various design demands,which come in the form of constraint in the optimization problem.Meanwhile,the minimization of the total mass would be of practical importance for the purpose of lightweight design.Compared with the existing concurrent optimization models[27,32,41]aiming at finding optimal configurations of macrostructures and microstructures with maximum structural stiffness or fundamental frequency,this paper aims to develop a novel concurrent optimization formulation based on the independent,continuous and mapping(ICM)method[42–44],in which the total mass of structure is minimized considering simultaneously load-carrying capabilities and thermal insulation properties.Structural responses at macro-and micro-levels are regarded as multiple constraints.Hence,the selection of weight coefficient in multi-objective design for multifunctional design can be avoided in previous study[28,31].By introducing the reciprocal variables,the objective function and constraint function can be explicitly approximated by the Taylor-series expansion method.Then the optimal problem can be effectively updated by sequential quadratic programming(SQP)algorithm,by setting up a series of sub-problems with the second order sensitivities.Some factors and parameters affecting the macrostructure or microstructure are also investigated.

The rest of this paper is structured as follows.Section 2 formulates the concurrent topology optimization problem of minimization of total mass with multiple constraints.Section 3 describes the homogenization procedure for effective material properties and sensitivity analysis with respect to macro-and micro-scale density variables.Section 4 introduces the design variables to conduct the standard quadratic programming.Section 5 describes the filtering schemes to eliminate numerical instabilities.Section 6 presents 2D and 3D numerical examples to validate the effectiveness of the proposed optimization method.Section 7 draws the concluding remarks.

2 Concurrent topology optimization for minimization of total mass with multiple constraints

In this paper,it is assumed that the macrostructure is composed of periodic cellular units(PCUs)as indicated in Fig.1.Both macrostructure and microstructure are discretized by finite element(FE).Each element on macro-scale or micro-scale level is assigned an exclusive density,namely macro-elemental densityPi(i=1,2,...,M)or microelemental densityr j(j=1,2,...,N),whereMandNare the total number ofFE in macrostructure and microstructure,respectively.In the PCU,r j=1 indicates that thejth element is occupied by base material whiler j=0 when thejth element is void.Pi=1 means theith element is porous andPi=0 represents theith element is void whatever value ofr j.In the concurrent optimization,two sets of relative densities will be integrated into one system through homogenization theory.

The total mass of the structuremcan be calculated as

Fig.1 An illustration of a structure composed of periodic cellular units:a macrostructure;b periodic cellular units;c unit cell(microstructure)

whereViis theith elemental volume,andρiHis the homogenized density in the macrostructure which is expressed as

whereV jdenotes thejth elemental volume in the microstructure.ρdenotes the density of base material.

The FE equation of the static equilibrium can be written as

whereUandFrepresent the applied load vector and the nodal displacement vector of the macrostructure,respectively.Krepresents the global stiffness matrix of the macrostructure which can be assembled by the elemental stiffness matrixK i

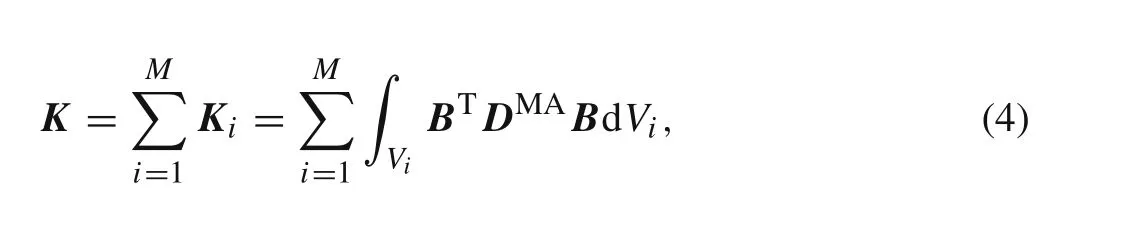
whereBis the strain-displacement matrix of the macrostructure.At the macro scale,theith elemental elastic matrixDMAis defined by

whereαis the exponent of penalization with the typical valueα=4 in this paper.DHis the effective elasticity matrix which can be computed through numerical homogenization.

The rigidity of the macrostructure can be measured in terms of nodal displacement,which can be calculated by multiplying a unit virtual load vectorΓand displacement vector.

whereΓis a vector consisting of zeros except for the positiona,corresponding to the concerned d.o.f.,where its value is one.

For the orthotropic material,the heat conduction capability can be evaluated in accordance with the summation of the diagonal elements in the effective thermal conductivity matrix.The thermal insulation constraint function for the 2D or 3D porous material can be stated as

whereκHssis thesth diagonal element in the effective thermal conductivity matrix.¯κis the upper bound for the final design.For anisotropic material,the non-diagonal elements can be non-zero.In this study,geometrical symmetries on bothxandyaxis are imposed on the microstructure for the design of orthotropic material.

In this study,the concurrent topology optimization aims at finding the minimization of total mass considering rigidity of macrostructure and thermal insulation capabilities of porous material simultaneously.The optimization problem can be mathematically stated as

From Eq.(9),we can observe that the objective function of total mass depends on both the macro-scale and micro-scale density variables.The constraint functions also include both macrostructural responsesdkand effective thermal conductivity related to the microstructure.It is a typical two-scale topology optimization problem where the optimized topologies of macrostructure and microstructure should be achieved simultaneously.

3 Homogenization and sensitivity analyses on both the macro-scale and micro-scale

The micro-elemental elastic matrix and thermal conductivity matrix are interpolated by SIMP scheme as

whereβrepresents the micro penalization power with the value of4 in this work.D0andκ0denote the elasticity matrix and the thermal conductivity matrix when the corresponding element is solid.When the PCU is small enough in comparison to the size of the macrostructure,the effective elasticity matrixDHin Eq.(5)can be calculated through homogenization theory[45]

where|V|is the volume ofPCU;Iis identity matrix;banduare the strain-displacement matrix and displacement vector for the microstructure,respectively.

To obtain the displacement vectoru,the PCU is analyzed by applying the periodic boundary conditions

The right-hand side term of Eq.(12)denotes the external forces caused by the uniform strain fields,e.g.two normal unit strains inxandydirections and one shear unit strain for 2D cases.

Similarly,the homogenized heat conductivity matrix can be calculated as

whereIsdenotes identity matrix for thermal conductivity homogenization,χrepresents the induced temperature gradient field,which can be computed from uniform gradient temperature.

For numerical homogenization expressed by Eqs.(11)and(13),more details on implementation can be referenced in Ref.[45].

With the aid of interpolation scheme in Eq.(10),the sensitivity of the homogenized elasticity tensor and thermal conductivity with respect tor jcan be conducted as

The sensitivities of nodal displacement with respect to the macro-densityPiand micro-densityr jare obtained through adjoint method as[46]

where¯Urepresents the adjoint displacement vector of macrostructure,which can be obtained via solving the following adjoint equation

In Eq.(15),the sensitivities of global stiffness matrixKwith respect toPiandr jcan be given based on Eqs.(4),(5),(11),and(14)

4 Introduction of design variables and formulation of quadratic programming

We notice that multiple constraints are present in Eq.(9),which needs to be solved by a mathematical programming algorithm.In this section,we will introduce design variables to make the constraint functions linearization by means of Taylor series expansion.

In this study,the design variables are defined as the reciprocal function of density variables,i.e.

The derivations ofPiorr jwith respect to design variables are expressed by

where superscript(b)is the number of the optimization iteration.

In the same way,we have

In Eqs.(21)and(22),the sensitivities ofdkandκHsswith respect to the design variables are calculated by the chain rule as follows

According to Eqs.(1)and(18),the total massmcan be rewritten as

whereGandHare the first order derivative matrix and the Hessian matrix,respectively.

The first-order and second-order derivatives of the total mass with respect to design variables can be calculated as follows

In Eq.(26),the constantm(b)can be omitted for objective function.By combining Eqs.(21),(22),and(26),the mathematical optimization model determined by Eq.(9)can be rewritten as

It is worth pointing out that Eq.(28)is in the form of a standard quadratic programming problem.Optimum values of design variables are updated by SQP algorithm efficiently.Then the macrostructure and microstructure are rebuilt by renewed densities according to Eq.(19)until the following criterion is satisfied as

whereεis the precision of convergence.

5 Elimination of numerical instabilities

To avoid unfavorable phenomena in topology optimization,i.e.checkerboard patterns and mesh dependence,the sensitivity filter technique is widely used in topology optimization.In this paper,instead of filtering the sensitivity of the objective function in SIMP method,the first term of constraint function in Eq.(21)is taken as the filtered variable as

The filter is implemented by solving the Helmholtz partial differential equation(PDE)with Neumann boundary conditions[47]

It can be proved that

From Eq.(32),the sum of filtered variables before and after filtering remains the same.The optimization procedure can benefit from such preserving feature which leads to a stable convergence.After filtering,the modified sensitivities expressed in Eq.(33)will replace the original sensitivities to update design variables.

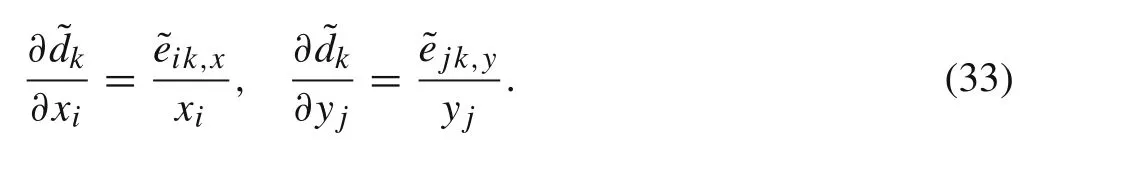
The filtering scheme brings blur boundary in final topologies on both macro-and micro-scales.To eliminate the immediate density,the filtering programs are terminated after convergence and the optimization procedure proceeds until meeting the condition described in Eq.(29)again.For the whole process,εis prescribed to be 0.1%and 0.01%before and after filtering.

6 Numerical examples and discussions

It is a usual practice in macro-scale topology optimization to adopt uniformly distributed material as the initial design to avoid local optimal solutions.However,it is infeasible in the inverse homogenization because the homogeneous sensitivity field generated by periodic boundary conditions will result in the halt of the optimization procedure.Following Amsturz et al.[48],the domain of PCU is assumed to be square with the edge length l.A circular region with the diameterDcomposed of softer material is defined at the center of PCU as shown in Fig.2.

Fig.2 Density distribution of initial design

To illustrate the capability and effectiveness of the proposed method,we present several numerical examples,for concurrently designing macrostructures and microstructures.The following material parameters are used for isotropic base material:Young’s modulusE=210 GPa,Poisson’s ratioν=0.3,densityρ=7800 kg/m3,and heat conductivityk=40 W/(m·K).For comparison,the normalized objective functionm/m0is used,in whichmandm0denote the total mass of the optimal structure and the initial structure full of materials,respectively.All numerical examples are run on a desktop computer with an Intel i7 2.93 GHz processor.

6.1 Example I

In the first example,a short cantilever beam is optimized to illustrate the effect of initial design on finial topologies.Figure 3 shows the admissible design domain in macrostructure with lengthL=120 cm,heightH=60 cm,and thicknessT=1 cm undergoing a concentrated vertical loadF=100 kN at the center of the right edge.The left side is fully constrained.The 2D design domain is discretized into 4-node plane strain elements with an edge length of 1 cm.The following constraints should be satisfied: (1) nodal distributions of material are investigated with the diameterD=5l/8,l/2,and 3l/8.The PCU is discretized into 80×80 4-node quadrilateral elements.The density is distributed uniformly with the value of 0.9 and 0.45 outside and inside the circle for three initial designs.No symmetric constraints are imposed on macrostructure and microstructure in this example.The optimized macrostructure,microstructure,and the corresponding material properties are summarized in Table 1.

From Table 1,the results give the similar macrostructure,but distinct microstructure compared to each other.As expected,optimized topologies of both macrostructure and microstructure possess geometric symmetry.In all cases,the resulting nodal displacement constraint and effective conductivity agree wellwith prescribed values.Three massfractions of the final design are close to each other.Therefore,it can be inferred that optimized topologies of microstructure are affected by initial design,which has similarities to material design.Results from the first initial design provide the minimum mass and its corresponding microstructure is simpler than two others.

To illustrate the effectiveness of the proposed method,the conventional SIMP method is adopted,i.e.Eq.(9)is updated directly by the Method of Moving Asymptotes(MMA)[49].Initial design in Table 1 with the diameterD=5l/8 is adopted.Optimized topologies of macrostructure and microstructure shown in Fig.4 are similar to those obtained by the proposed method.These results verify the effectiveness of the present approach.

Fig.3 2D macro-structural design domain for the concurrent optimization in Example I,with the dimension:length L=120 cm,height H=60 cm with thickness T=1 cm.The left side is fully constrained and a concentrate vertical load F=100 kN is applied at the center of the right edge

6.2 Example II

From Fig.5,we can observe that optimized topologies of microstructure share similar configurations when the thermal-insulating capability of porous material is set to be a constant.In contrast,macrostructure depends obviously on different displacement constraint values imposed at pointA.It is seen that a larger mass fraction can be achieved with a more strict control on the displacement of macrostructure.It is intuitively easy to understand because the structure with a larger mass fraction possesses sufficient rigidity to resist elastic deformation.

6.3 Example III

This example is also the extension of Example I,which is considered in an attempt to reveal the influence of effective conductivity constraint on the final results.The nodal displacement constraint is fixed asu A?−0.5 cm.The upper bound for the effective conductivity varies from 36 to 48 W/(m·K).Other parameters are the same as those chosen in Example I.Figure 6 shows the mass fraction for various upper bounds of the effective thermal conductivity with typical topologies of macrostructure and microstructure inserted.

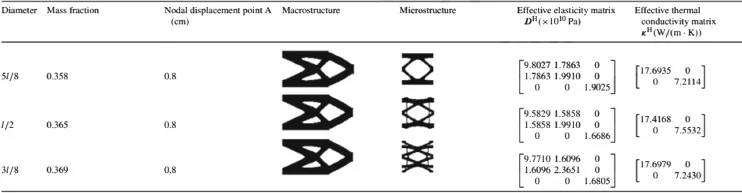
Table 1 Optimal results for different initial design

Fig.4 Optimized topologies obtained from MMA algorithm for:a macrostructure;b microstructure

Fig.5 Evolution history of the total mass with the increasing upper bound of effective thermal conductivity and the corresponding structural evolution for Example II

In this example,we can find that optimized topologies of macrostructure share similar configurations for different conductivity constraint values when the nodal displacement constraint is fixed.However,the conductivity constraint values have a greater impact on the mass fraction of macrostructure and the volume fraction and optimal topology of microstructure.The mass fraction of macrostructure decreases monotonously with the increase of the conductivity constraint values,in contrast to the increase in the volume fraction of microstructure.Compared with results in Fig.5,because more emphasis is placed on thermal insulating properties of porous material,more material is shifted from micro level to macro level automatically.The optimal results have demonstrated that the proposed concurrent optimization method can distribute the base material between macrostructure and microstructure to meet the requirements of light weight design and various constraints simultaneously.

Fig.6 Evolution history of the total mass with the increasing low bound of nodal displacement,and the corresponding structural evolution for Example III

6.4 Example IV

From Fig.7,it can be seen that the mass fractions for various low bounds of nodal displacement show the same tendency as that previously reported in Example 1.However,a slight difference can be found in optimized topologies of microstructure,which implies that,in spite of the same thermal insulation constraint,the microstructure may be affected by the variation of prescribed nodal displacements in macrostructure.

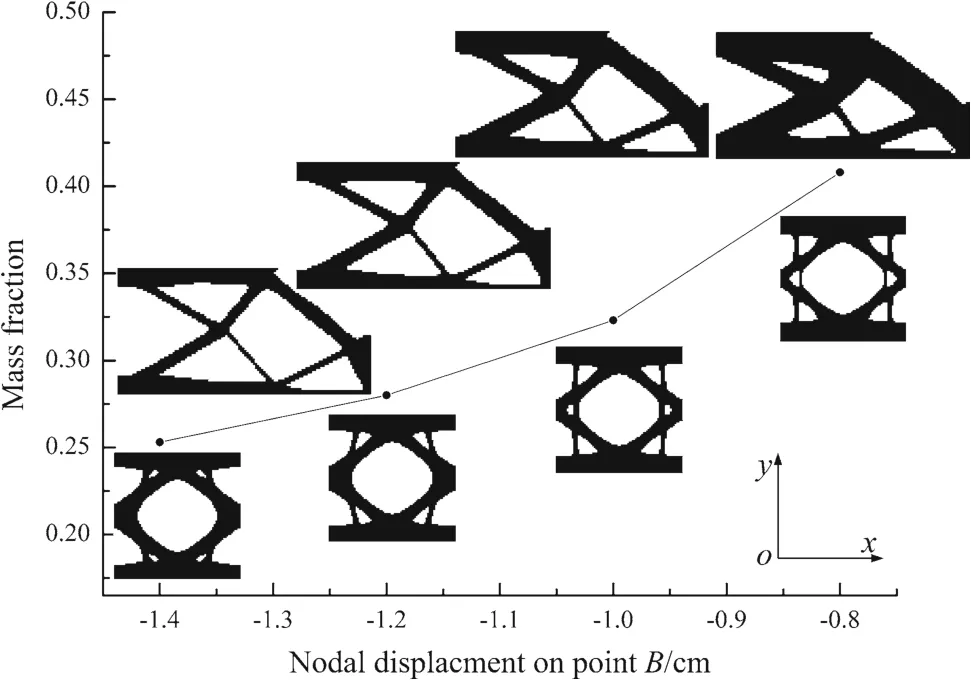
Fig.7 Evolution history of the total mass with the increasing low bound of nodal displacement,and the corresponding structural evolution for Example IV

6.5 Example V

This example is the extension of Example II,specifically used for evaluating the effect of multiple nodal displacement constraints on optimized topologies.As depicted in Fig.3,two concentrated loads,acting in opposite directions,are imposed on pointB(downward)and pointC(upward)for loading case I and II,respectively.In loading case I,the constraint value of vertical displacement on pointCis prescribed asu C?0.9 cm as the first constraint.In loading case II,the low bound for the vertical displacement on pointBare investigated which varies from−0.8 to−1.1 cm.The symmetries inxandydirections are enforced on the microstructure for obtaining orthotropic material.Other parameters are the same as those chosen in Example II.Figure 8 presents the mass fraction for various low bounds of nodal displacement with optimal macro and micro topologies inserted.

Apparently,optimal topology of macrostructure is symmetric only when nodal displacement constraint is prescribed to be symmetric in different loading cases.With more stringent requirements for the stiffness concerned with the macrostructure,the mass fraction increase monotonously at the macro level while the resulting topologies of the microstructure have no significant difference from each other.Seeking for a lightweight design,both load-carrying capabilities of the macrostructure in multiple loading cases and requirement of thermal insulation related to cellular material can be balanced by the proposed method.

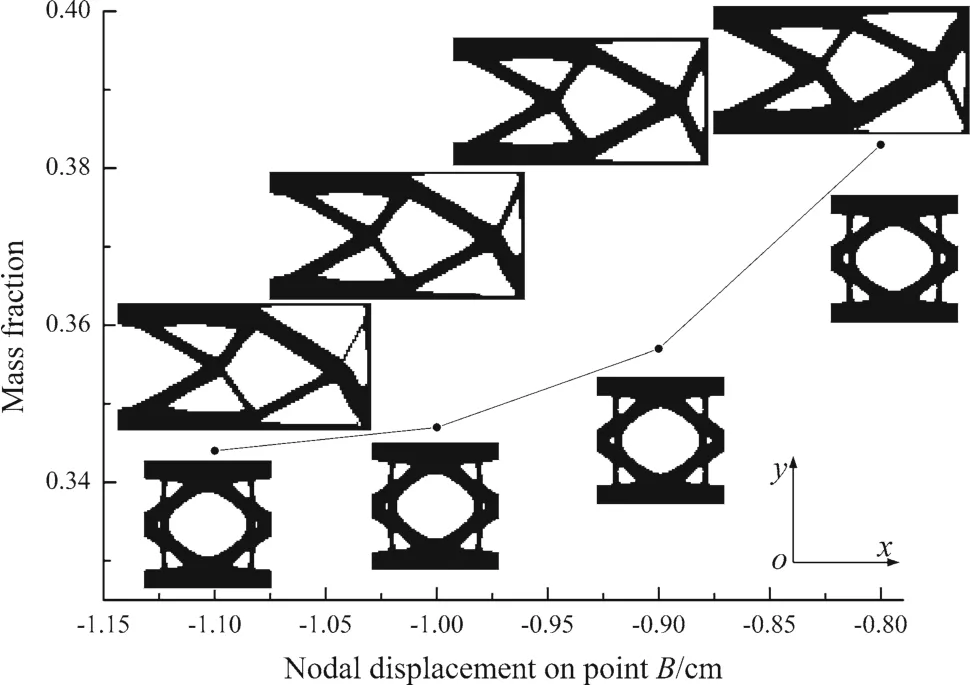
Fig.8 Evolution history of the mass fraction with the increasing low bound of nodal displacement,and the corresponding structural evolution for Example V

6.6 Example VI

This example optimizes a typical 3D structure,aiming to illustrate the feasibility of the proposed approach in 3D structure.Figure 9 shows the admissible design domain in macrostructure,which is discretized by brick elements with the size:lengthL=48 cm,widthB=30 cm,and heightH=6 cm.The size of the elements is 1 cm.The microstructure is discretized into 26×26×26 solid elements.The left surface is fully constrained and a concentrate forceF=1×104kN is applied on the centre of the right surface.

When we fixed the low bound of nodal displacement asu A?−1.0 cm,the upper bound for the effective conductivity varies from 30 to 40 W/(m·K).Figure 11 presents the mass fraction for various upper bounds of the effective thermal conductivity with optimal macro and micro topologies inserted.The final microstructure is symmetrical.

Similar to 2D cases,Figs.10 and 11 also demonstrate that the two-scale optimal design is a compromising solution between the thermal insulation of materials and structural stiffness at macro level.The weight fractions of final design share the similar tendency as those illustrated in 2D cases.

It is worth pointing out that topology optimization of 3D structure is time-consuming.In the present concurrent optimization model,there are six numerical homogenization analyses involving mechanical properties and three numerical homogenization analyses involving thermal properties for each iteration step.Table 2 provides a comparison of the iteration steps and computational cost(CPUtime in seconds)for six different FE discretization meshes.The optimized topologies of microstructure for different discretization meshes are also shown in Fig.12.As can be seen from Table 2,the CPU time increases dramatically as mesh density increases.It is normal for optimization methods to need more design iterations,when increasing the mesh density[46],especially for 3D structure.However,the presented method can provide a solution in which number of iterations is independent of discretization mesh.Figure 12 also demonstrates that optimized topologies are independent of the discretization mesh.The slight difference between these topologies is that the boundary becomes smoother with finer mesh.

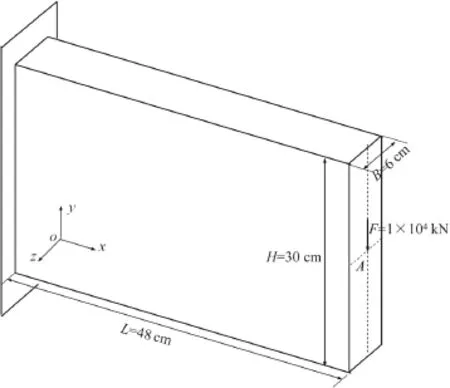
Fig.9 3D macrostructural design domain for the concurrent optimization in Example VI,with the dimension:length L=48 cm,width B=30 cm and height H=6 cm.The left surface is fully constrained and a concentrate force F=1×104 kN is applied on the centre of the right surface

Fig.10 Evolution history of the mass fraction with the increasing low bound of nodal displacement,and the corresponding structural evolution for Example VI

Fig.11 Evolution history of the mass fraction with the increasing upper bound of effective thermal conductivity and the corresponding structural evolution for Example VI

Table 2 Iteration steps and CPU time for different FE discretization meshes

7 Conclusion

In this present paper,a novel concurrent topology optimization formulation for minimization of total mass considering load bearing in macrostructure and thermal insulation of porous material simultaneously is proposed,which is distinct with the existing concurrent topology optimization approaches.For a typical two-scale optimization problem,the objective function of total mass involves the macroscale and micro-scale density.The material properties from homogenization of microstructure are applied to macrostructural analysis,while the sensitivities of the microstructure are related to the displacement vectors of macrostructures obtained from original and adjoint load cases.With the introduction of reciprocal variables,the constraint functions are linearized while the objective function is approximated as the second order Taylor expansion.Then the established optimization model can be solved efficiently using SQP algorithm,by setting up a series of sub-problems in the form of a quadratic program with second-order sensitivities.

As highlighted in the provided numerical examples,the proposed concurrent optimization method can automatically allocate the base material between macrostructure and microstructure to meet the requirements various constraints simultaneously to achieve a lightweight design.Because of its generality,this method can be extended to the structural design considering other design requirements,such as the frequency constraints.

AcknowledgementsThe project was supported by the National Natural Science Foundation of China(Grants 11202078,51405123)and the Fundamental Research Funds for the Central Universities(Grant 2017MS077).We are thankful for Professor Krister Svanberg for MMA program made freely available for research purposes.

Fig.12 Optimized topologies for different FE discretization meshes:a 22×22×22;b 26×26×26;c 30×30×30;d 34×34×34;e 38×38×38;f 42×42×42

1.Bendsøe,M.P.,Kikuchi,N.:Generating optimal topologies in structural design using a homogenization method.Comput.Methods Appl.Mech.Eng.71,197–224(1988)

2.Bendsøe,M.P.:Optimal shape design as a material distribution problem.Struct.Optim.1,193–202(1989)

3.Zhou,M.,Rozvany,G.I.N.:The COC algorithm,Part II:topological,geometrical and generalized shape optimization.Comput.Methods Appl.Mech.Eng.89,309–336(1991)

4.Xie,Y.M.,Steven,G.P.:Asimple evolutionary procedure for structural optimization.Comput.Struct.49,885–896(1993)

5.Huang,X.,Xie,Y.M.:Convergent and mesh-independent solutions for the bi-directional evolutionary structural optimization method.Finite Elem.Anal.Des.43,1039–1049(2007)

6.Wang,M.Y.,Wang,X.,Guo,D.:A level set method for structural topology optimization.Comput.Methods Appl.Mech.Eng.192,227–246(2003)

7.Sethian,J.A.,Wiegmann,A.:Structural boundary design via level set and immersed interface methods.J.Comput.Phys.163,489–528(2000)

8.Allaire,G.,Jouve,F.,Toader,A.M.:Structural optimization using sensitivity analysis and a level-set method.J.Comput.Phys.194,363–393(2004)

9.Zhou,S.,Wang,M.Y.:Multimaterial structural topology optimization with a generalized Cahn–Hilliard model of multiphase transition.Struct.Multidiscip.Optim.33,89(2007)

10.Guo,X.,Zhang,W.,Zhong,W.:Doing topology optimization explicitly and geometricallyła new moving morphable components based framework.J.Appl.Mech.81,081009(2014)

11.Guo,X.,Zhang,W.,Zhang,J.,et al.:Explicit structural topology optimization based on moving morphable components(MMC)with curved skeletons.Comput.Methods Appl.Mech.Eng.310,711–748(2016)

12.Zhang,W.,Zhang,J.,Guo,X.:Lagrangian description based topology optimization—a revival of shape optimization.J.Appl.Mech.83,041010(2016)

13.Zhang,W.,Yang,W.,Zhou,J.,et al.:Structural topology optimization through explicit boundary evolution.J.Appl.Mech.84,011011(2016)

14.Zhang,W.,Chen,J.,Zhu,X.,et al.:Explicit three dimensional topology optimization via moving morphable void(MMV)approach.Comput.Methods Appl.Mech.Eng.322,590–614(2017)

15.Guo,X.,Zhou,J.,Zhang,W.,et al.:Self-supporting structure design in additive manufacturing through explicit topology optimization.Comput.Methods Appl.Mech.Eng.323,27–63(2017)

16.Eschenauer,H.A.,Olhoff,N.:Topology optimization ofcontinuum structures:a review.J.Appl.Mech.Appl.Mech.Rev.54,331–390(2001)

17.Rozvany,G.I.N.:A critical review of established methods of structural topology optimization.Struct.Multidiscip.Optim.37,217–237(2009)

18.Sigmund,O.,Maute,K.:Topology optimization approaches.Struct.Multidiscip.Optim.48,1031–1055(2013)

19.Sigmund,O.:Materials with prescribed constitutive parameters:an inverse homogenization problem.Int.J.Solids Struct.31,2313–2329(1994)

20.Sigmund,O.:Tailoring materials with prescribed elastic properties.Mech.Mater.20,351–368(1995)

21.Clausen,A.,Wang,F.,Jensen,J.S.,et al.:Topology optimized architectures with programmable Poisson’s ratio over large deformations.Adv.Mater.27,5523–5527(2015)

22.Xie,Y.M.,Yang,X.,Shen,J.,etal.:Designing orthotropic materials for negative or zero compressibility.Int.J.Solids Struct.51,4038–4051(2014)

23.Wang,X.,Xu,S.,Zhou,S.,et al.:Topological design and additive manufacturing of porous metals for bone scaffolds and orthopaedic implants:a review.Biomaterials 83,127–141(2016)

24.Rodrigues,H.,Guedes,J.M.,Bendsoe,M.P.:Hierarchical optimization of material and structure.Struct.Multidiscip.Optim.24,1–10(2002)

25.Coelho,P.G.,Fernandes,P.R.,Guedes,J.M.,et al.:A hierarchical model for concurrent material and topology optimisation of threedimensional structures.Struct.Multidiscip.Optim.35,107–115(2008)

26.Liu,L.,Yan,J.,Cheng,G.:Optimum structure with homogeneous optimum truss-like material.Comput.Struct.86,1417–1425(2008)

27.Niu,B.,Yan,J.,Cheng,G.:Optimum structure with homogeneous optimum cellular material for maximum fundamental frequency.Struct.Multidiscip.Optim.39,115–132(2009)

28.Deng,J.,Yan,J.,Cheng,G.:Multi-objective concurrent topology optimization of thermoelastic structures composed of homogeneous porous material.Struct.Multidiscip.Optim.47,583–597(2013)

29.Guo,X.,Zhao,X.,Zhang,W.,et al.:Multi-scale robust design and optimization considering load uncertainties.Comput.Methods Appl.Mech.Eng.283,994–1009(2015)

30.Huang,X.,Zhou,S.W.,Xie,Y.M.:Topology optimization of microstructures of cellular materials and composites for macrostructures.Comput.Mater.Sci.67,397–407(2013)

31.Yan,X.,Huang,X.,Sun,G.,et al.:Two-scale optimal design of structures with thermal insulation materials.Compos.Struct.120,358–365(2015)

32.Liu,Q.,Chan,R.,Huang,X.:Concurrent topology optimization of macrostructures and material microstructures for natural frequency.Mater.Des.106,380–390(2016)

33.Xu,B.,Jiang,J.S.,Xie,Y.M.:Concurrent design of composite macrostructure and multi-phase material microstructure for minimum dynamic compliance.Compos.Struct.128,221–233(2015)

34.Xu,B.,Xie,Y.M.:Concurrent design of composite macrostructure and cellular microstructure under random excitations.Compos.Struct.123,65–77(2015)

35.Xu,B.,Huang,X.,Xie,Y.M.:Two-scale dynamic optimal design of composite structures in the time domain using equivalent static loads.Compos.Struct.142,335–345(2016)

36.Zhang,W.,Sun,S.:Scale-related topology optimization of cellular materials and structures.Int.J.Numer.Methods Eng.68,993–1011(2006)

37.Xia,L.,Breitkopf,P.:Concurrent topology optimization design of material and structure within FE2nonlinear multiscale analysis framework.Comput.Methods Appl.Mech.Eng.278,524–542(2014)

38.Xia,L.,Breitkopf,P.:Recent advances on topology optimization of multiscale nonlinear structures.Arch.Comput.Methods Eng.24,227–249(2016)

39.Jia,J.,Cheng,W.,Long,K.,et al.:Hierarchical design of structures and multiphase material cells.Comput.Struct.165,136–144(2016)

40.Long,K.,Han,D.,Gu,X.:Concurrent topology optimization of composite macrostructure and microstructure constructed by constituent phases of distinct Poisson’s ratios for maximum frequency.Comput.Mater.Sci.129,194–201(2017)

41.Chen,W.,Tong,L.,Liu,S.:Concurrent topology design of structure and material using a two-scale topology optimization.Comput.Struct.178,119–128(2017)

42.Sui,Y.,Peng,X.:The ICM method with objective function transformed by variable discrete condition for continuum structure.Acta Mech.Sin.22,68–75(2006)

43.Sui,Y.,Yang,D.:Anew method for structural topological optimization based on the concept of independent continuous variables and smooth model.Acta Mech.Sin.14,179–185(1998)

44.Sui,Y.:Modelling,Transformation and Optimizationł New Developments of Structural Synthesis Method.Dalian University of Technology Press,Dalian(1996)

45.Andreassen,E.,Andreasen,C.S.:How to determine composite material properties using numerical homogenization.Comput.Mater.Sci.83,488–495(2014)

46.Zuo,Z.H.,Xie,Y.M.:Evolutionary topology optimization of continuum structures with a global displacement control.Comput.Aided Des.56,58–67(2014)

47.Lazarov,B.S.,Sigmund,O.:Filters in topology optimization based on Helmholtz-type differential equations.Int.J.Numer.Methods Eng.86,765–781(2011)

48.Amstutz,S.,Giusti,S.M.,Novotny,A.A.,etal.:Topological derivative for multi-scale linear elasticity models applied to the synthesis of microstructures.Int.J.Numer.Methods Eng.84,733–756(2010)

49.Svanberg,K.:The method of moving asymptotes-a new method for structural optimization.Int.J.Numer.Methods Eng.24,359–373(1987)