基于前向补偿的再入飞行器制导控制一体化设计*
2018-04-18郭建国张添保
周 军,郭建国,张添保
(西北工业大学 精确制导与控制研究所·西安·710072)
0 引 言
制导控制系统是飞行器实现飞行任务的关键,对于再入飞行器而言,同样具有重要的使命。而制导控制一体化技术更能使得制导控制系统发挥出整体的性能[1]。
自1983年Williams等[2]提出了制导控制一体化设计这一概念以来,经国内外众多专家、学者的不懈努力,制导控制一体化设计已经取得了一定的成果[3-9]。文献 [4]针对拦截弹纵向平面,通过坐标转换和滑模控制的方法设计了制导控制一体化设计系统;Wang等[5]基于自适应滑模控制给出了终端角度约束下的制导控制一体化设计方法;文献 [6]采用小增益原理,利用滑模变结构方法设计了高超声速飞行器再入段满足参考轨迹跟踪的制导控制一体化方法;文献 [7]利用干扰观测器,结合加幂积分方法与嵌套饱和方法设计了一体化控制方法,解决了高超声速飞行器俯冲段饱和控制问题;文献 [8]考虑了姿态控制通道间耦合因素,结合反步法与块动态逆方法设计了制导与控制一体化算法;文献 [9]通过求导得到了制导控制一体化低阶设计模型,利用滑模控制方法完成了飞行器俯冲段制导控制一体化设计。
由于飞行器制导控制一体化模型是一个含有不确定性的非匹配的控制系统,所以反演法常常作为一个有效的方法来完成一体化设计。本文针对再入飞行器打击机动目标,考虑了制导控制一体化中的耦合问题,采用干扰观测器和滑模控制方法,一方面有效地抑制了未知不确定性,另一方面有效地消除了制导控制一体化中的耦合影响。通过仿真验证了该方法的有效性。
1 面向控制的一体化模型
1.1 相对运动学模型
大气层内再入飞行器和机动目标的相对运动学模型可表示为[10]
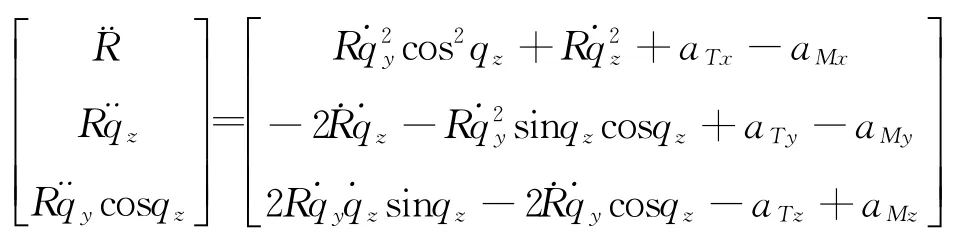
式中,q z和q y分别为飞行器和目标的视线倾角和视线偏角;R为相对距离;a Tx、a Ty、a Tz分别为目标加速度在视线系下的分量;a Mx、a My、a Mz分别为飞行器加速度在视线系下的分量。
1.2 飞行器姿态控制模型
再入飞行器的姿态控制系统的模型可表示为[11]
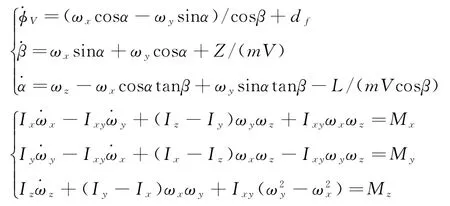
式中,φV、β和α分别为飞行器的倾侧角、侧滑角和攻角;ωx、ωy和ωz分别为飞行器的旋转角速度;L和Z分别为飞行器的升力和侧向力;d f为不确定性;I x、I y和I z分别为飞行器体系下的三轴转动惯量;I xy为交叉惯量;M x、M y和M z分别为飞行器体系下的气动力矩。
1.3 一体化模型
为了便于一体化设计,可以将气动力和气动力矩进行分解,建立如下形式的制导控制一体化模型:

式中,f1、f2和f3是已知的非线性项,d1、d2和d3是未知的不确定项。
假设1:模型 (1)的干扰项存在上界、且干扰的一阶导数也存在上界,即
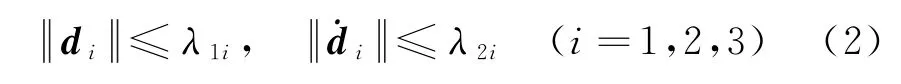
式中,λ1i、λ2i分别为d i和̇d i的上确界。
1.4 非线性干扰观测器设计
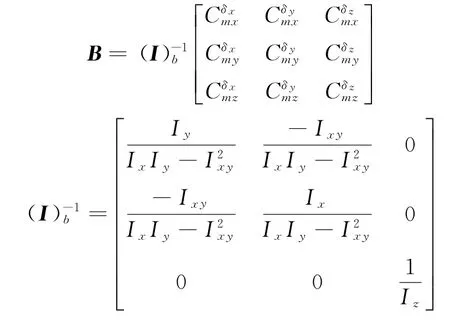
为了能够提高制导控制系统的精度,针对一体化模型设计非线性干扰观测器,实时估计模型的非匹配性干扰d1、d2和匹配性干扰d3。根据参考文献 [12],模型 (1)的干扰观测器方程为

式中:
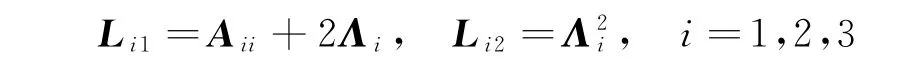
其中,Λ1=diag(Λ11,Λ12),Λ2=diag(Λ21,Λ22,Λ23)和Λ3=diag(Λ31,Λ32,Λ33)均为正定矩阵。
根据文献 [12]可知,观测器式 (3)能使观测值和真实值之间满足
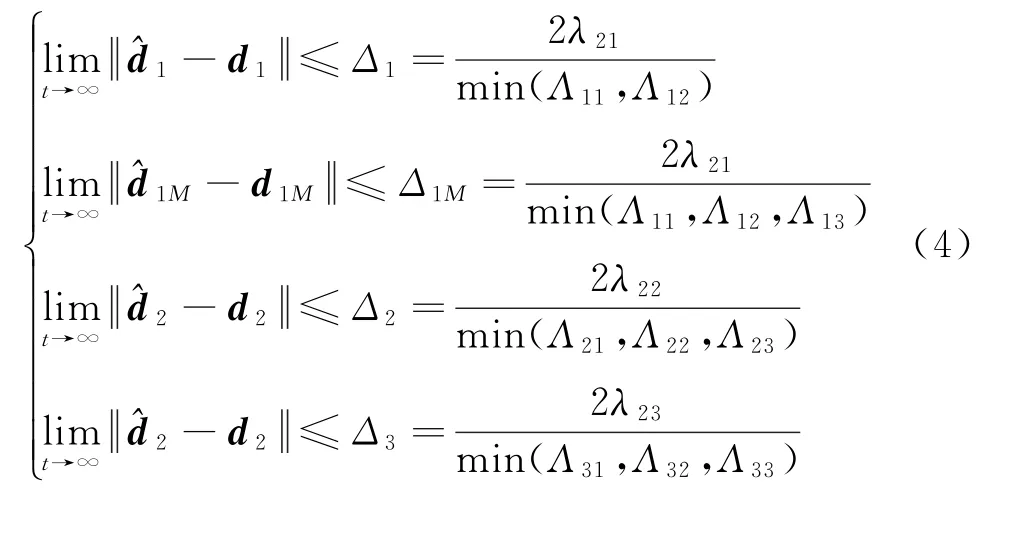
2 传统的制导控制一体化设计
针对第1节建立的制导控制一体模型,利用设计的干扰观测器实施估计干扰,再利用反演法和滑模控制方法设计制导控制一体化控制律,具体可得如下的定理1,实现制导控制一体化的有限时间稳定。
定理1:对于一体化制导控制模型式 (1),若采用干扰观测器式 (3)对不确定性进行实时估计,则采用如下的传统一体化制导控制律
其中的参数满足
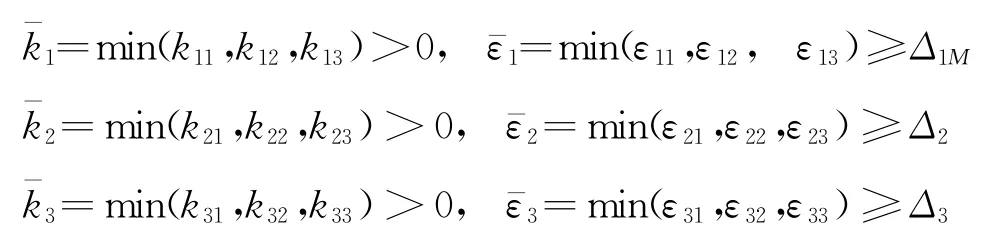
则可使得系统为有限时间稳定。
证明:定义Lyapunov函数为
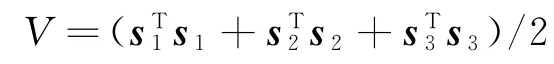
则其一阶导为
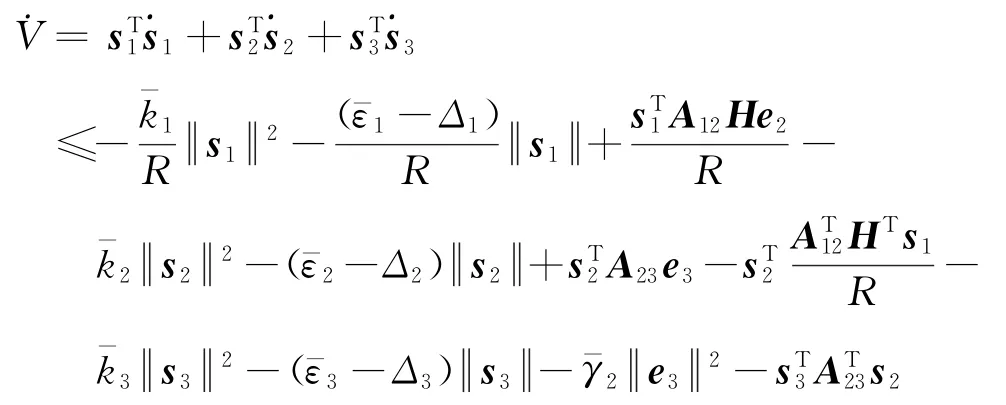
由控制器参数和式 (4),可得

由李雅普诺夫稳定性定理可知,飞行器在一体化制导控制律式 (5)的作用下,能使控制系统中状态为有限时间到达滑模面,而滑模面即为跟踪误差,因此可使得系统状态的跟踪误差有限时间稳定。证毕。
这种一体化控制律采用的滑模相对简单,在稳定性证明中需要提高符号函数的增益以抑制系统中的耦合因素,为此,本文进一步改进了滑模的设计,消除这些耦合项。
3 基于前向补偿的一体化设计
利用反演法和滑模控制方法,设计前向补偿的制导控制一体化控制律,具体可得如下的定理2,同样也实现了一体化的有限时间稳定。
定理2:对于一体化制导控制模型式 (1),若采用干扰观测器式 (3)对干扰进行实时估计,则采用如下的一体化制导控制律
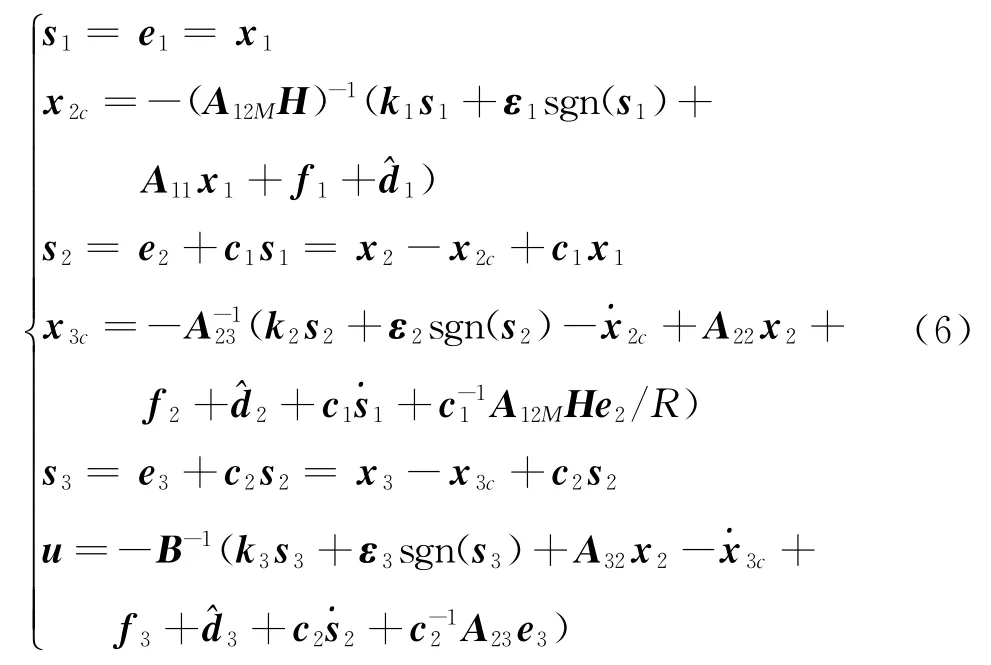
其中的参数满足
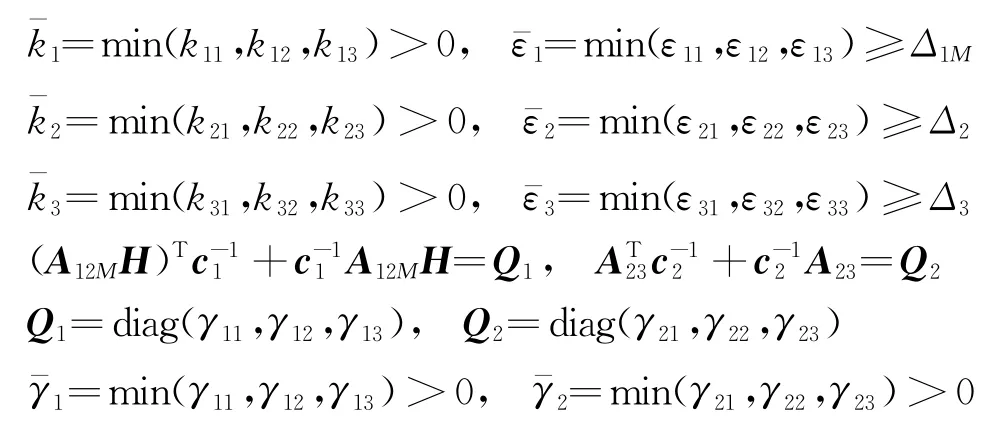
则可使得系统为有限时间稳定。
证明:定义Lyapunov函数为
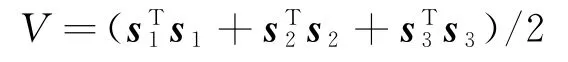
则其一阶导为

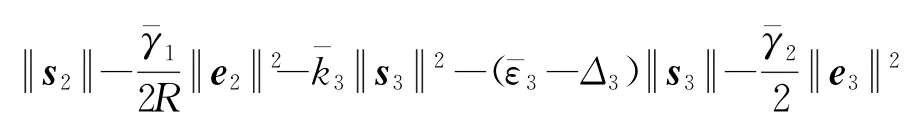
因此,系统状态能够在有限时间收敛于滑模面。当s i=0,i=1,2,3时,由于S=CE,式中S=[s1,s2,s3]T,E=[e1,e2,e3]T,
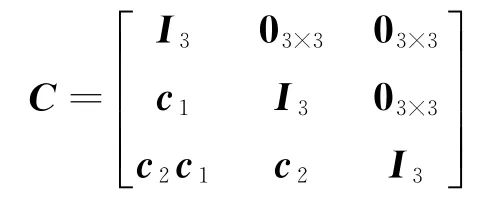
则有E=C-1S, 当S=[s1,s2,s3]T=0时,有E=0。因此,系统状态跟踪误差与滑模面一样为有限时间稳定。证毕。
由于x2c和x3c不连续,其微分不存在。其微分量可采用低通滤波器近似获得,采用低通滤波器获取一阶微分,其形式为:
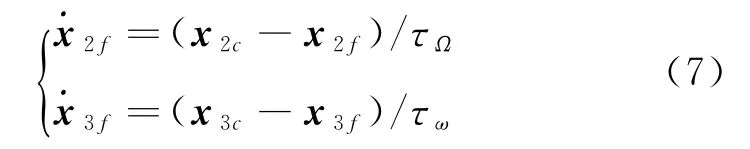
式中,τΩ、τω均为滤波时间常数,取值为正数。
则在制导控制系统中,可采用̇x2f代替̇x2c、采用̇x3f代替̇x3c。
4 仿真分析
这里分别对分离制导控制 (SGC)系统设计方法、传统一体化制导控制 (TIGC)系统设计方法和前向补偿一体化制导控制 (FCIGC)系统设计方法进行对比仿真。仿真条件为:
飞行器初始状态为
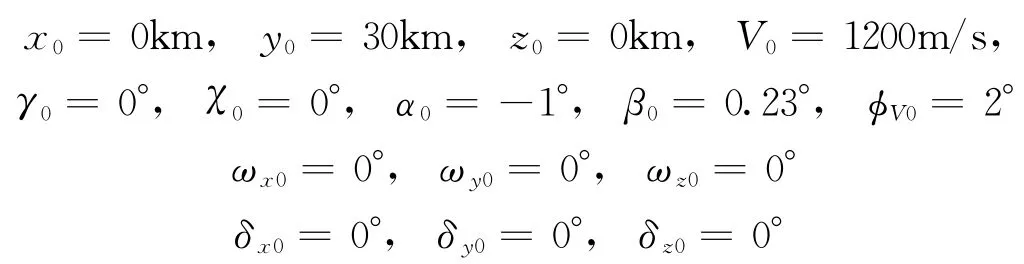
目标初始状态为
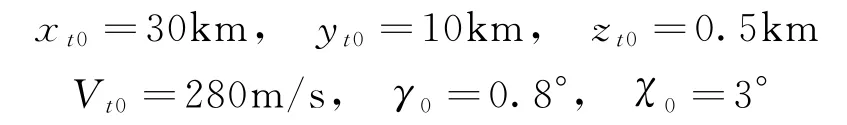
目标速度机动形式为正弦机动
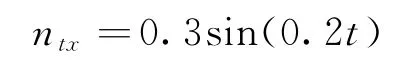
侧向和法向机动为等幅螺旋机动
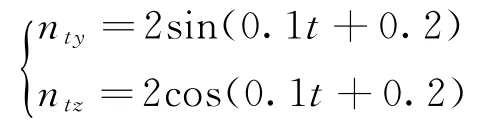
制导控制参数选为
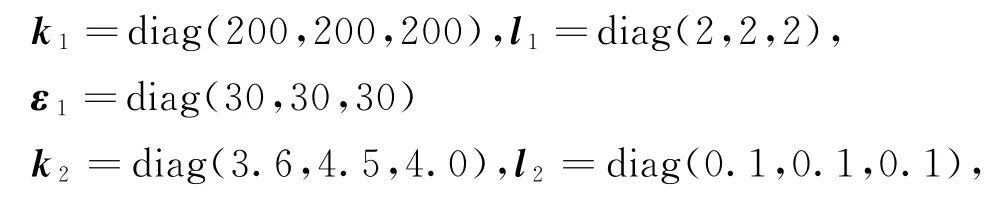
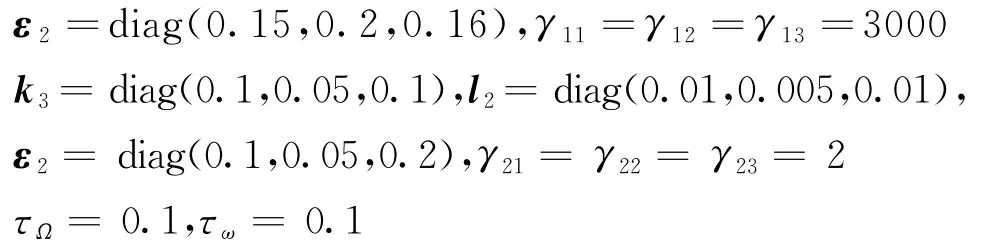
仿真实验结果如图1~图10所示。图1所示为三种方法下飞行器与目标的运动轨迹变化情况,图2和图3给出了三种方法下视线角速率变化情况,显然三种方法均能有效地控制视线角速率稳定,最后视线角速率的分散是由于相对距离不断减少所产生的。

图1 三维飞行运动轨迹对比图
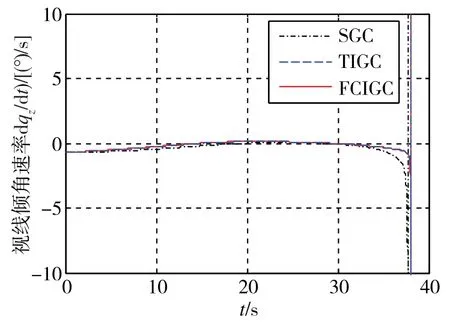
图2 视线倾角速率变化对比图
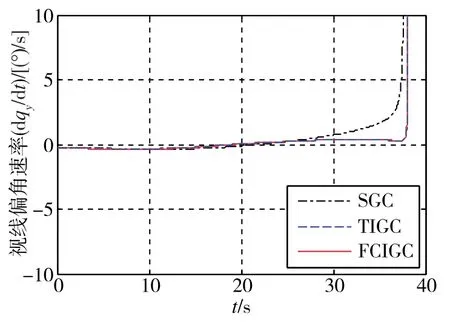
图3 视线偏角速率变化对比图
图4~图6分别给出了飞行器攻角、侧滑角和倾侧角的变化情况,从图4和图6可以看出,TIGC方法和FCIGC方法下的攻角和倾侧角变化比SGC方法更平缓,主要是在TIGC方法和FCIGC方法下的动态特性更好。
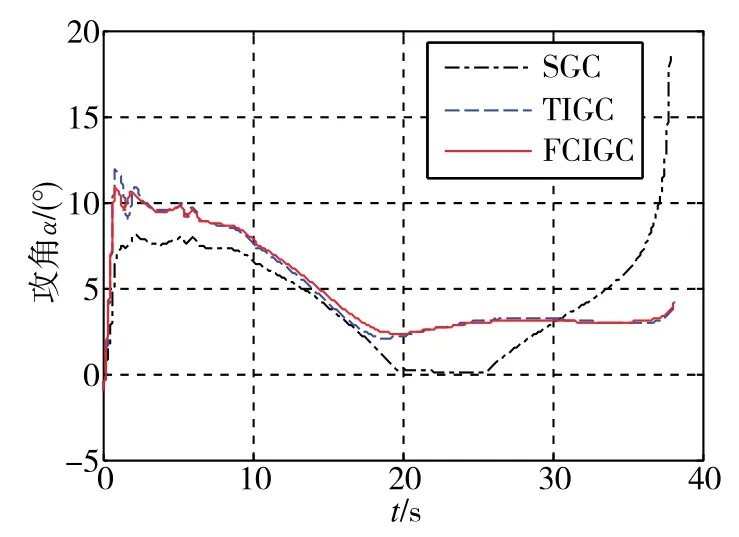
图4 攻角跟踪曲线
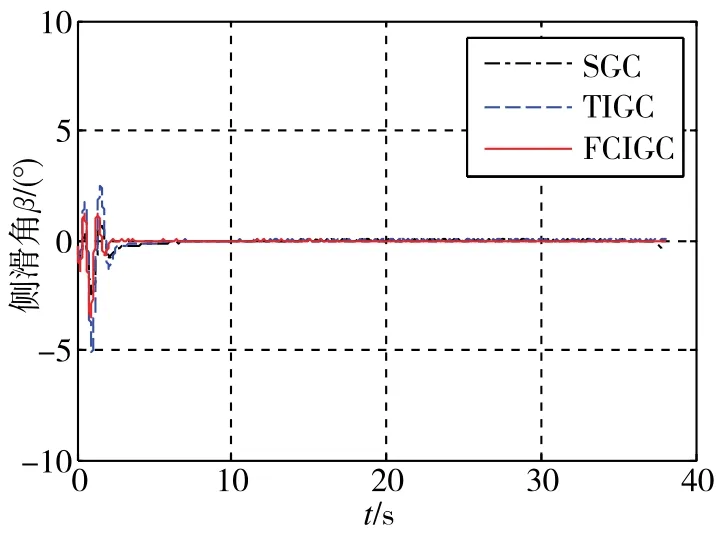
图5 侧滑角变化对比图

图6 倾侧角变化对比图
图7~图9分别给出了俯仰、偏航和滚动通道上的舵面偏转情况,FCIGC方法下的舵偏角相对较小,且变化比较平稳,特别是在22s附近没有出现波动,稳定性较好。
为了进一步考核制导控制系统的性能,将考虑导引头测量噪声和气动参数随机拉偏来进行蒙特卡洛打靶仿真分析,取气动参数拉偏范围为±20%,随机拉偏比例服从 [-20%,20%]间的均匀分布,随机产生蒙特卡洛拉偏数据组合500组进行综合仿真。三种方法下500次仿真的脱靶量分布如图10~图12所示,从而得到脱靶量正态分布计算结果如表1所示,显然看到,所设计的FCIGC方法比传统一体化设计方法和分离设计方法具有更好的制导精度和鲁棒性。
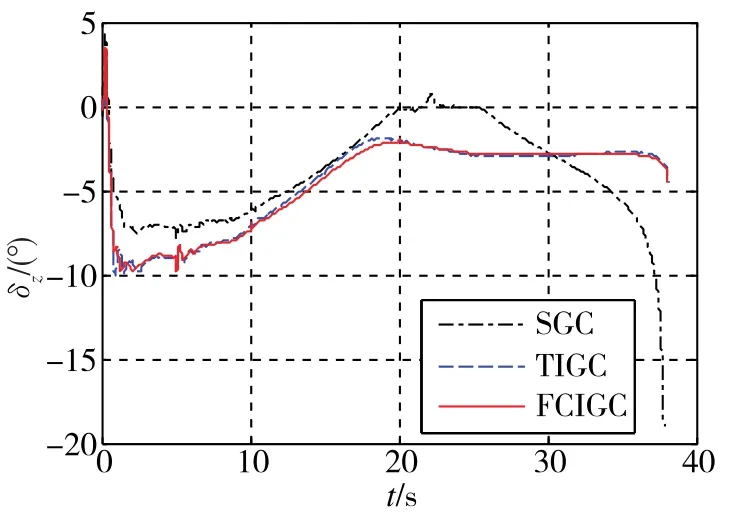
图7 俯仰舵偏角变化对比图
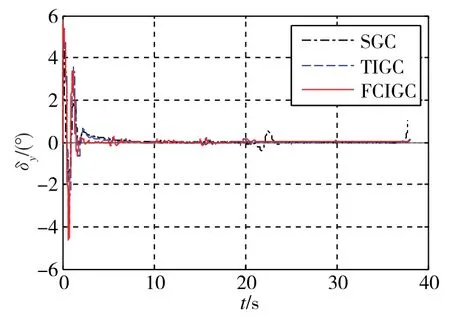
图8 偏航舵偏角变化对比图

图9 滚转舵偏角变化对比图
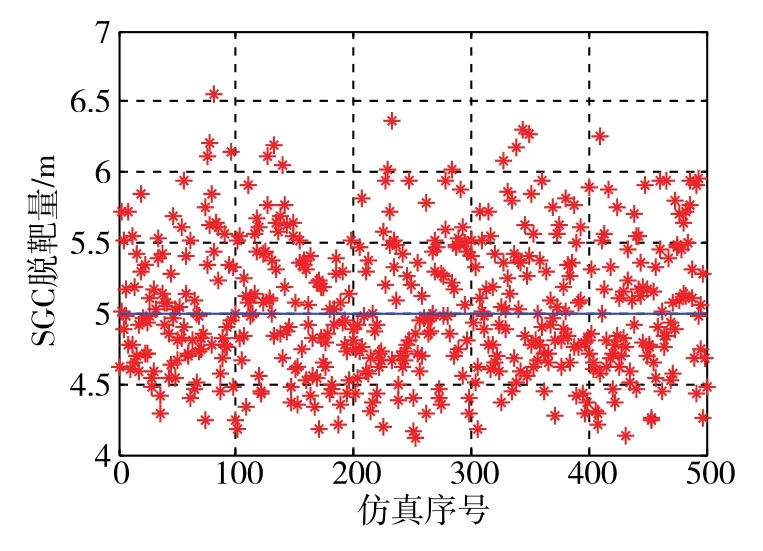
图10 500次仿真SGC脱靶量
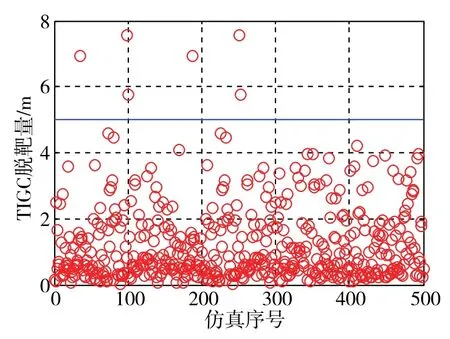
图11 500次仿真TIGC脱靶量
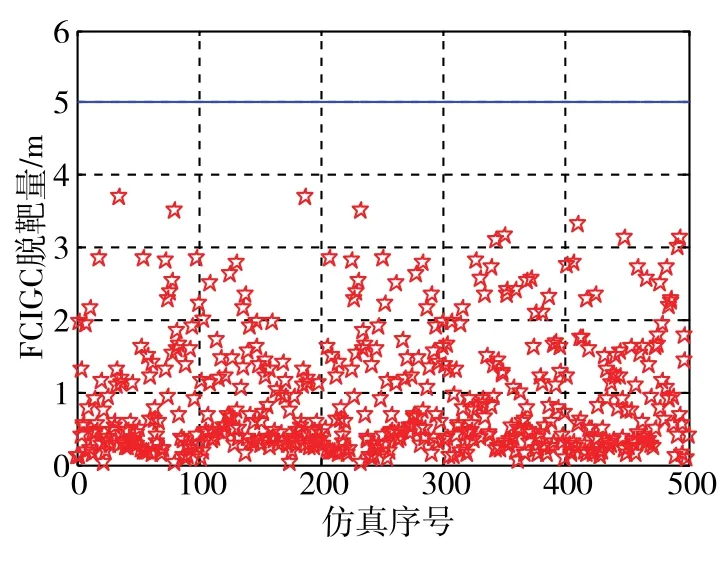
图12 500次仿真FCIGC脱靶量

表1 三种方法下脱靶量正态分布计算结果
5 结 论
本文针对再入飞行器设计了具有前向补偿的制导控制一体化系统。采用非线性干扰观测器估计未知不确定性,同时利用反演法和滑模控制方法,有效地消除了系统间的耦合特性,并保证了制导控制系统的有限时间稳定。仿真结果表明:与分离制导控制系统、传统的制导控制一体化系统相比,前向补偿的制导控制一体化系统具有良好的制导性能和鲁棒性。
