地震初至震相自动识别方法研究

李恩来，王承伟，安祥宇

（辽宁省地震局，辽宁 沈阳110034）

0 引言

在传统地震学中，地震震相的拾取一般采用人工分析的方式，虽然精度较高，但效率低。随着地震台网的不断发展和台站密度的不断增加，记录的数据量也不断增加，特别是实时地震学的发展，简单的人工拾取震相已不能满足要求，对震相的自动精确拾取成为地震学家日益关注的问题，同时也发展了多种地震震相识别方法。

目前，绝大多数震相自动识别方法是提取信号和噪声的不同特征来作为提取震相到时的判据，比如用波形的幅值变化、频率变化、地震波形的相关性和运动学特征等来判别地震震相类型。归纳起来，常用的判别方法有：能量变化方法、偏振分析方法、自回归方法（ARAIC）以及神经网络方法等。能量方法中最常用的为短长时间平均（STA/LTA）方法［1，3-6］，短长时间平均方法反应了幅值的瞬时变化，短时平均代表能量的瞬时变化，长时平均代表能量的稳态变化。震相到来时，质点运动的偏振方向会发生改变，地震波的偏振分析由于提取出了地震波的偏振特征经常被用在震相捡拾和判别震相类型［2，7-9］。自回归方法是假定可以把地震波划分为局部平稳段，并且在触发点前后是不同的平稳过程［10］。根据这个假定AR-AIC通常被用作P 波和S波的自动捡拾中［11-12］。不同于AR-AIC算法，Maeda（1985）提出了一种不用求AR系数的时域AIC方法［14］，Zhang 等（2003）应用基于小波变换的AIC方法，直接对小波系数应用AIC方法［13］。Baiand Kennett（2000）指出目前存在的震相自动识别方法中没有哪一种可以捡拾出所有的震相到时，各种方法都有其局限性，特别是信噪比的影响［15］。比如，在噪声较高或者事件淹没在前面事件的尾波中，最常用的能量方法就不能有效识别震相，或者拾取的震相误差较大。本文使用最常用的短长时窗能量比（STA/LTA）加自回归方法（AIC）的方式，采用两步法进行初至震相识别，并分析特征函数对能量变化的敏感度，得到了比较好的结果。

1 震相识别的基本原理

1.1 长短时窗能量比（STA/LTA）方法

我们给出一定长度的滑动长时窗，再在这个长窗中取一个固定时长的短时窗，两窗口的起点或者终点重合，然后求取短时间窗内信号的平均值（STA）和长时间窗内信号的平均值的比值，用这个比值来反映信号幅值或者能量的变化。其中，STA主要反映的是信号瞬时变化的平均值，LTA主要反映的是背景噪声变化的平均值。在地震信号到达时，STA的变化要比LTA的变化大的多，STA/LTA值会有明显的增加。我们设定一个阈值，当STA/LTA值大于该阈值时，即认为有震相到达， 从而达到自动识别震相的目的。

其中，i为采样时刻；ns为短时窗长度；nl是长时窗长度；λ为设定的触发阈值；CF（j）为在j时刻的关于信号的特征函数值，表示信号的振幅、能量或其变化。

1.2 自回归方法（AIC）

七十年代，日本学者Akaike提出一个基本信息量的定阶准则，即AIC准则。地震震相到时识别的自回归（AR）技术是假设震相到时前后的地震记录是两个不同的稳态过程。不同于AR-AIC方法，Maeda（Maeda N.1985）建议可由地震波形数据在时域直接计算AIC函数，而不需要求出AR 系数，对地震记录x（i）（i=1，2，…， L）来说，AIC检测器定义为：

AIC（k）=k·log｛var（x［1，k］）｝+（L-k-1）·log｛var（x［k+1，L］）｝ （2）

其中，k的范围为地震图某窗口内所有的采样点；var 表示方差。震相到时对应于AIC函数的最小值。

本文中，我们不在地震图上直接应用AIC准则，而是在用STA/LTA方法粗略捡拾到P 波位置后，在固定窗内用地震记录的垂直向特征函数来进行精确识别震相，即在粗略捡拾点向前和向后截取一定长度的时间窗，在窗内应用AIC准则，窗内AIC的最小值，即认为是精确到时点。因为在对P 波进行STA/LTA 粗略捡拾时，其得到的触发点一般滞后于真实触发点，所以在本文中我们对P 波捡拾后，在拾取到的P 波位置处向前推100个数据点，向后推10个数据点，即对采样频率为100Hz的地震记录，前推时间为1s，后推时间为0.1s。

2 特征函数分析

在STA/LTA方法中，特征函数的选择对震相识别至关重要，选择特征函数应遵循如下原则：能灵敏地反映地震信号到达时其振幅和频率的变化特征，并能增强这些变化。目前常用的特征函数有如下五个：

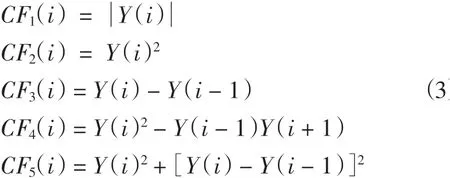
本文分别测试了上述五个特征函数对频率和振幅变化的响应，并作了分析。

2.1 特征函数对振幅变化的响应

为了测试上述特征函数对振幅变化的响应，生成一个余弦信号，频率为40Hz，在信号的先后两段，振幅相差2 倍。

图1 特征函数对振幅变化的响应（a 为原始波形，b-f分别为各特征函数对信号的响应）Fig.1Responseof eigenfunctionstoamplitudechanges

由测试结果可见，五个特征函数对振幅变化都有响应，但响应的结果明显不同，CF1、CF3、CF5对振幅的响应幅度较小，且响应处两边毛刺较大。CF2对振幅的响应较大，但响应处两边同样存在较大的毛刺。CF4对振幅的响应最为明显，响应处振幅较大，光滑，两边无毛刺。

2.2 特征函数对频率变化的响应

为了测试特征函数（公式（3））对频率变化的响应，生成一个余弦信号，在信号的先后两段，频率相差2 倍。

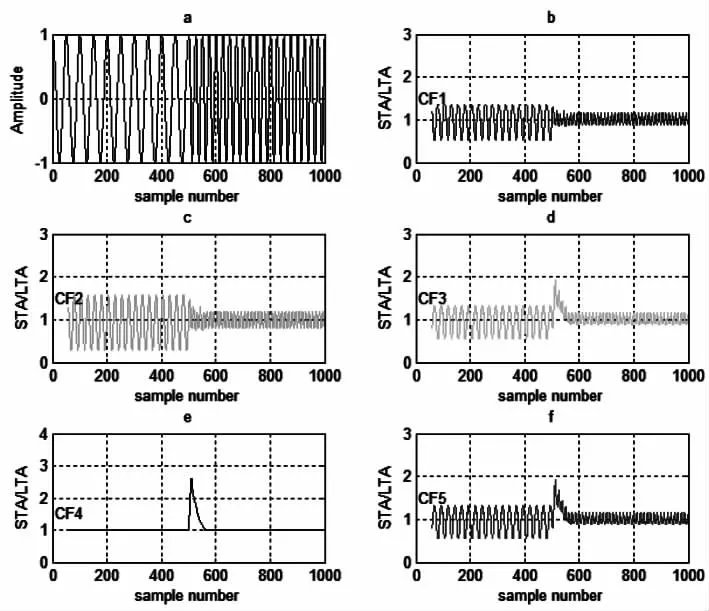
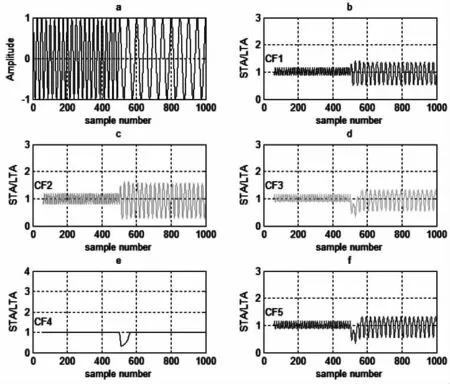
图2 特征函数对振幅变化的影响（a 为原始波形，b-f分别为各特征函数对改信号的响应）Fig.2 Responseof eigenfunctions tofrequencychanges

从测试结果可见，5个特征函数随频率变化都有不同程度的响应，其中，CF1、CF2对频率变化的响应不明显。CF3和CF5对频率的变化有响应，但响应处两侧的毛刺较多。CF4对频率的响应最强，响应光滑且两边无毛刺现象。

总之，经过上述测试，发现CF4（第四个特征函数）对振幅和频率的变化均表现出非常好的敏感性。因此，在对P 波初至震相进行拾取时，选择CF4做为特征函数为最佳。

3 资料的选取

本研究共使用辽宁地区2010—2015年记录到的地震521个，因震级较小或者震中距较大都会造成记录的信号较弱，信噪比较低，影响震相的拾取精度。故选择台站记录的垂直分向（UD向），台站的震中距＜150 km，地震震级ML>2.0 级。所有事件的震中分布如下图所示。

台网保存的事件数据格式有两种，分别为SEED格式和EVT 格式。本文使用SEED格式，使用rdseed软件解压*.seed 波形事件文件，去除仪器响应，去均值、去倾斜校正，并进行带通滤波，滤波频率0.1～20Hz。

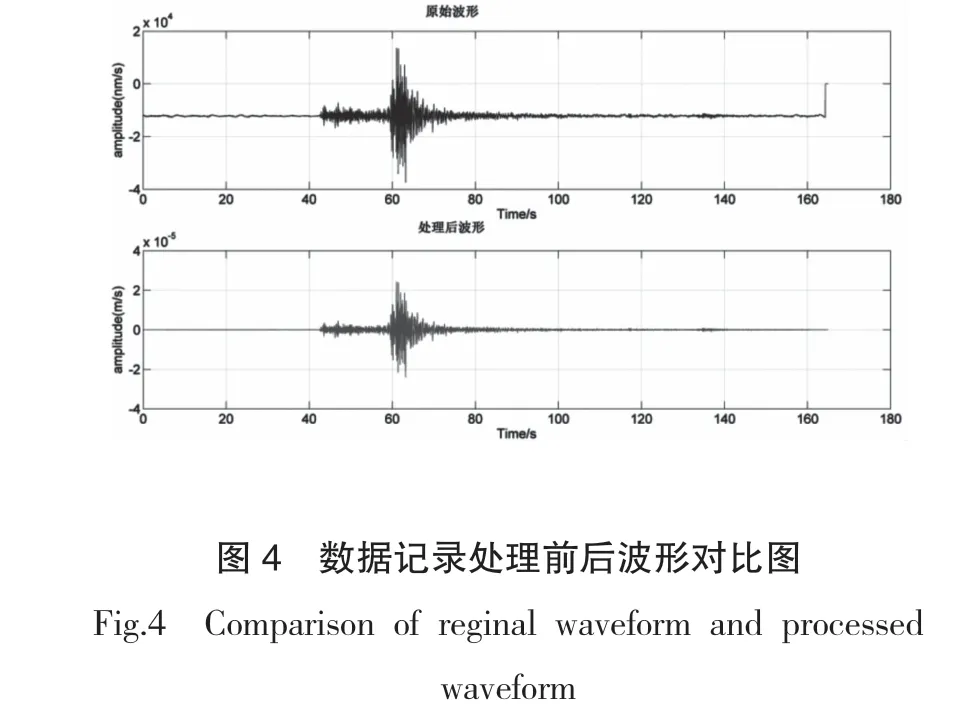
4 结果分析

本次计算共使用地震记录4662 条，其中检测到的地震记录4597个，未检测到地震记录65个，检测到的初至震相比例达到96.5%。通过与观测报告中人工拾取的初至震相到时对比，对拾取的震相到时进行分析。由图5可见，在检测到的所有记录中，大部分记录拾取的震相误差都0.5秒以内，达到3193条，误差1秒到2 秒的记录一秒的记录363个，其余的为误差1秒以上记录。从检测的结果总可以看到，该方法可以很好的对地震记录的初至震相进行拾取。

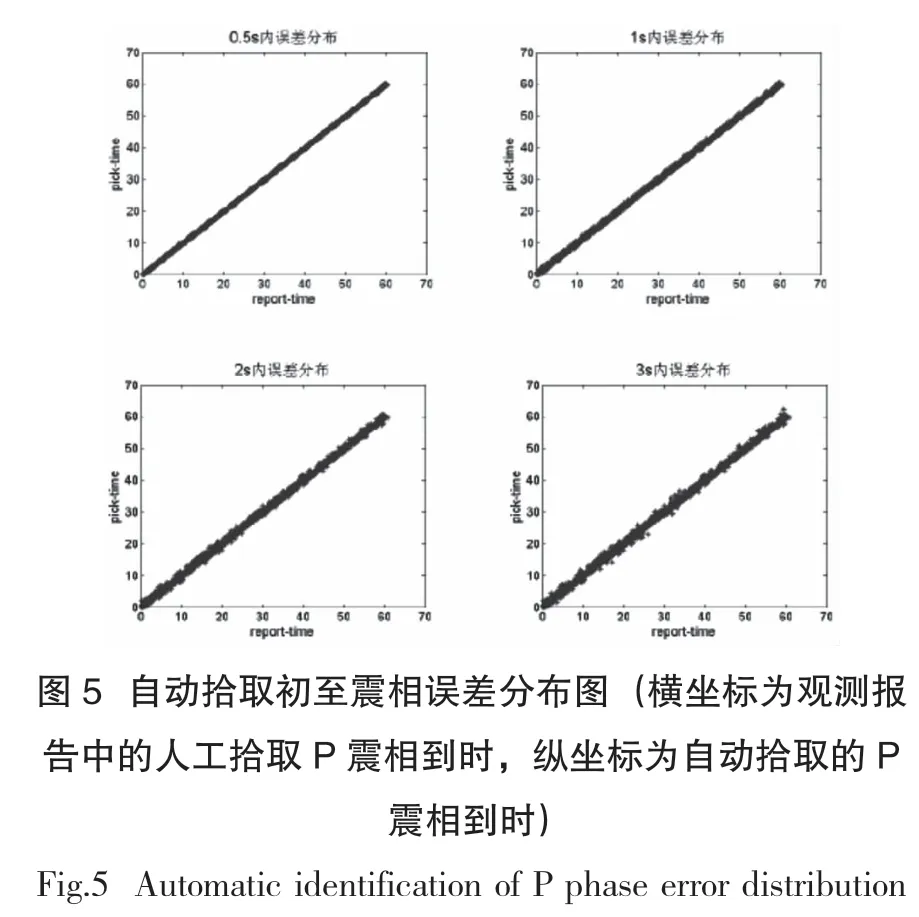
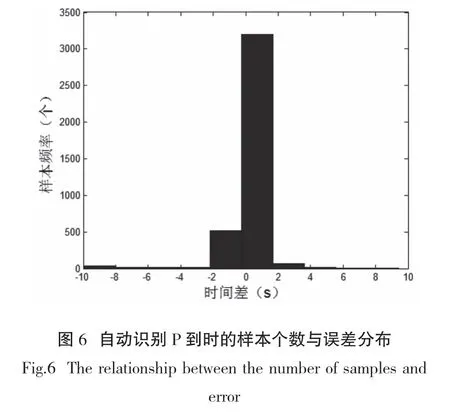
在所有使用的全部记录中，有65个未被检测到，还有个别拾取到时误差较大的记录，分析原因，主要为信噪比较低，干扰较大，或者有连续地震事件发生，且两地震的时间间隔很小，第二个事件的震相到时拾取误差较大，不能应用本文方法，需进一步分析研究。除此以外，通过分析发现，还有一些观测报告中震相拾取时间的明显错误。

5 结论和讨论

本文通过利用STA/LTA加AIC方法这种两步拾取地震波初至震相的方式，对辽宁台网近年来记录的地震初至震相进行了分析，认为本方法可以有效的自动识别较近震中距（150km）、信噪比较好的记录的初至震相。在分析的所有记录中，误差小于0.5秒的记录占到70%以上。同时对该方法中的特征函数（公式3）进行了分析，认为CF4无论对频率变化，还是对振幅变化，均表现出清晰的响应，所以在选择使用该方法时，应优先选择CF4作为特征函数。

该方法原理简单，操作便捷，能较好的识别初至震相，但也有其使用条件。在震中距较远、信噪比较小的情况下，可能会导致识别震相到时的误差较大，或者不能有效的识别震相；在有连续地震事件发生，特别是震群发生的情况下，由于事件波形间隔时间较短，或者后续事件淹没在前一事件当中时，该方法不适用。