基于地震时程分析的尾矿坝稳定性评价
2018-04-17郝喆
郝 喆
(1.辽宁大学 环境学院,辽宁 沈阳110036;2.辽宁有色勘察研究院,辽宁 沈阳110013)
0 引言
地震作用下,边坡稳定性评价有两类主要指标:地震永久变形和稳定安全系数[1]。
地震永久变形从滑体在地震力作用下的运动规律出发,计算其刚体位移,推求坝体可能发生的永久变形量。变形属于反映尾矿坝稳定状态的综合指标,显然要比单靠一个极限平衡的安全系数合理,其缺点是不如稳定系数直观,另外目前规范对尾矿坝的位移预警阈值仍没有准确界定。
安全系数是一个很直观的稳定性评价指标,尾矿库的设计及安全规范[2,3]推荐的也是安全系数法。地震分析时一般采用拟静力法,不考虑地振动频率、次数和持续时间,又未考虑坝身材料的动力性质和阻尼性质等[4],因而无法给出坝体在地震时的反应特性。规范[2]也指出,对于高烈度区的大型尾矿坝,除按拟静力法计算外,应开展专门的时程法抗震计算,弥补拟静力法计算的不足。时程分析法可给出动力抗滑稳定系数随时间的变化规律,较好地分析边坡的稳定状态。
有鉴于此,本文采用永久变形分析和地震时程分析相结合的综合分析方法,开展某大型尾矿坝的稳定性评价,为现场尾矿库提供更为可靠的稳定性判据。
1 现场概况
某尾矿库为山谷型,初期坝由碎石堆积而成;后期坝采用上游法尾砂筑坝,总坝坡比1 ∶4,子坝每次堆积高度2 m,按0.5m 层厚分层碾压或夯实,尾矿在坝前均匀堆放,保持坝体协调上升。现状坝顶标高约为226m,坝轴线长713 m,总坝高约为74m,全库容1600 万m3,堆积坝外坡比约为1 ∶4.0,干滩长度约为300 m(图1)。

图1 尾矿坝外坡面Fig.1Outsideslope surfaceof tailingsdam
尾矿库排洪方式采用排水井-排水隧洞(排水涵管)。坝体设有横纵向排水沟和横向排渗管。尾矿库设有坝体位移观测点和浸润线观测孔。
2 计算模型建立
2.1 工程地质剖面
据勘察报告给出的最大坝高工程地质主剖面建模,各土层分布情况与之一致(图2)。

图2 尾矿坝主剖面图Fig.2 Main profileof tailingsdam
2.2 计算参数选取
尾矿库地层由天然地层、尾矿堆积物及人工堆积层构成,天然地层、人工堆积层较为简单,尾矿堆积物构成及分布较复杂。根据岩土工程勘察报告,确定计算参数如表1所示。
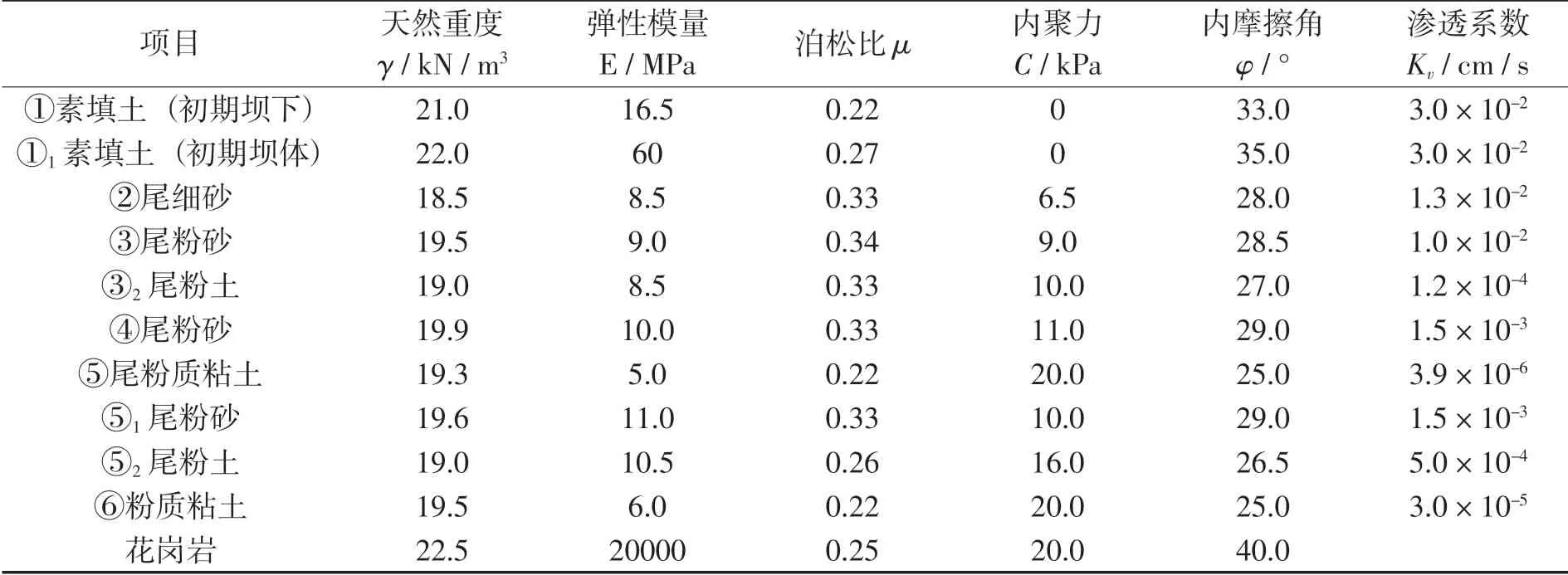
表1 岩土体物理力学参数推荐表
2.3 地震荷载确定
工程场地所在地区的基本设防烈度为Ⅶ度(0.10g)。坝体底部地面地震加速度分别采用工程场地50年超越概率10%、5%的时程输入曲线[5],如图3和图4所示。

图3 场地地表水平向地震时程曲线(50 年超越概率10%)Fig.3Horizontal seismictimehistorycurve of ground surface(10% Transcendentalprobability during 50 year)
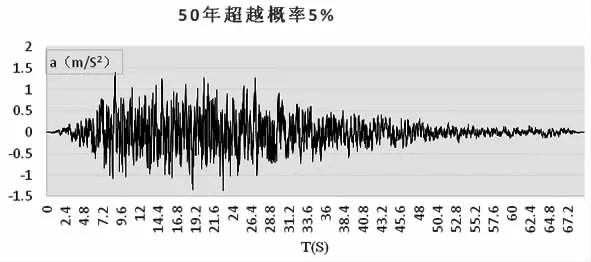
图4 场地地表水平向地震时程曲线(50 年超越概率5%)Fig.4 Horizontal seismictime history curve of ground surface(5%Transcendental probability during 50 year)
2.4 有限元网格划分
有限元计算模型按1∶1000的比例建立。网格划分如图5所示。

2.5 本构模型
采用“莫尔-库伦”模型和“修正UBCSAND”模型。修正UBCSAND是基于有效应力用塑性理论来模拟液化现象的模型[6],该模型在2D基础上扩展为3D应力状态,可以进行隐式非线性分析,适于模拟地震荷载作用下砂土液化现象。
2.6 人工边界
早期动力分析时,模型边界条件一般是远离计算区域设置固定边界或自由边界,不能模拟无限半空间中波动能量的传播过程,会导致波动能量在模型中反复反射传播而影响计算结果,计算精度低,尤其在输入动力荷载时程较长时边界的影响更突出,而且还会引起计算不收敛而无法完成动力分析[7]。为解决该问题,模型采用较先进的粘性边界,如图6所示。

3 尾矿坝地震动力分析
3.1 动力分析工况
考虑到同时遭遇设计频率的洪水和设防烈度地震的几率太小,设计频率的洪水不易形成稳定的浸润线,特殊运行工况中地震荷载不再与设计频率洪水位的渗透压力组合。在尾矿坝的地震动力计算中按尾矿库正常水位工况进行计算。
3.2 特征周期计算
尾矿坝形态与土层材料离散性的特征决定了尾矿坝的模态较多,显然绝大数的振型模态都是次要可忽略的,但为在振型叠加时取得更高的精度,在计算中取50阶进行计算。经计算得出,坝体在不同标高下的固有振型周期如表2所示。

表2 尾矿坝特征周期计算结果统计表
3.3 坝体永久变形分析
3.3.1 分析方法
坝体在地震荷载作用下的永久变形分析采用直接积分法[8],在各个地震时程荷载作用下的时间步骤按尾矿坝模型的特征周期的10~20%选取。以现状坝高工况为例,现状坝高的尾矿坝场地自振卓越周期为0.973s,那么计算时间步增量取0.2s,计算荷载总时程63s,总的计算步骤为315步。限于篇幅,仅以基本烈度下(50年超越概率10%)的永久变形分析为例。
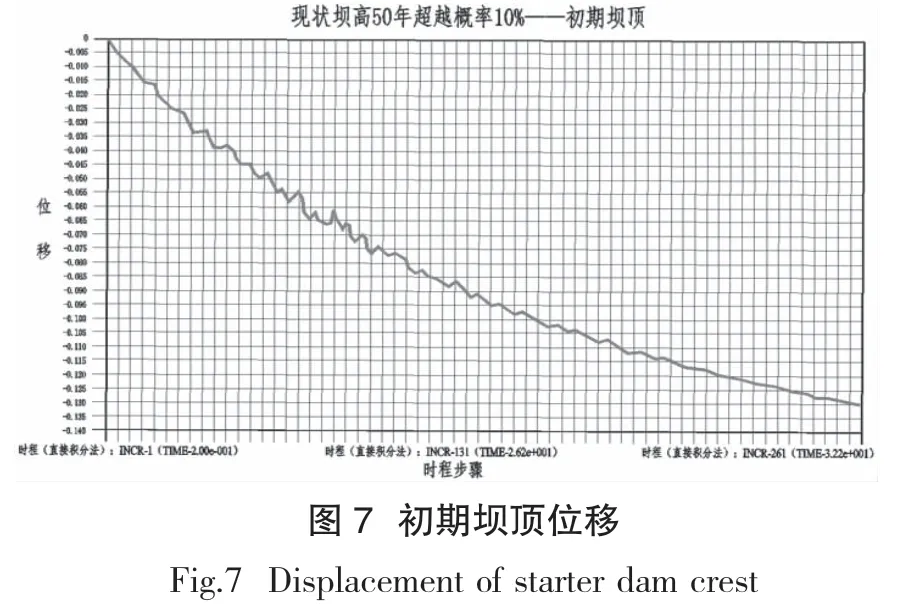
3.3.2 初期坝顶
初期坝顶位移曲线如图7所示。经计算,坝顶结点在地震荷载作用下的最终永久变形(塑性变形)约为0.14m。
3.3.3 堆积坝(坝高30m、50m 和滩顶)
尾矿坝在不同堆积标高时的坝顶位移曲线如图8所示,计算结果:
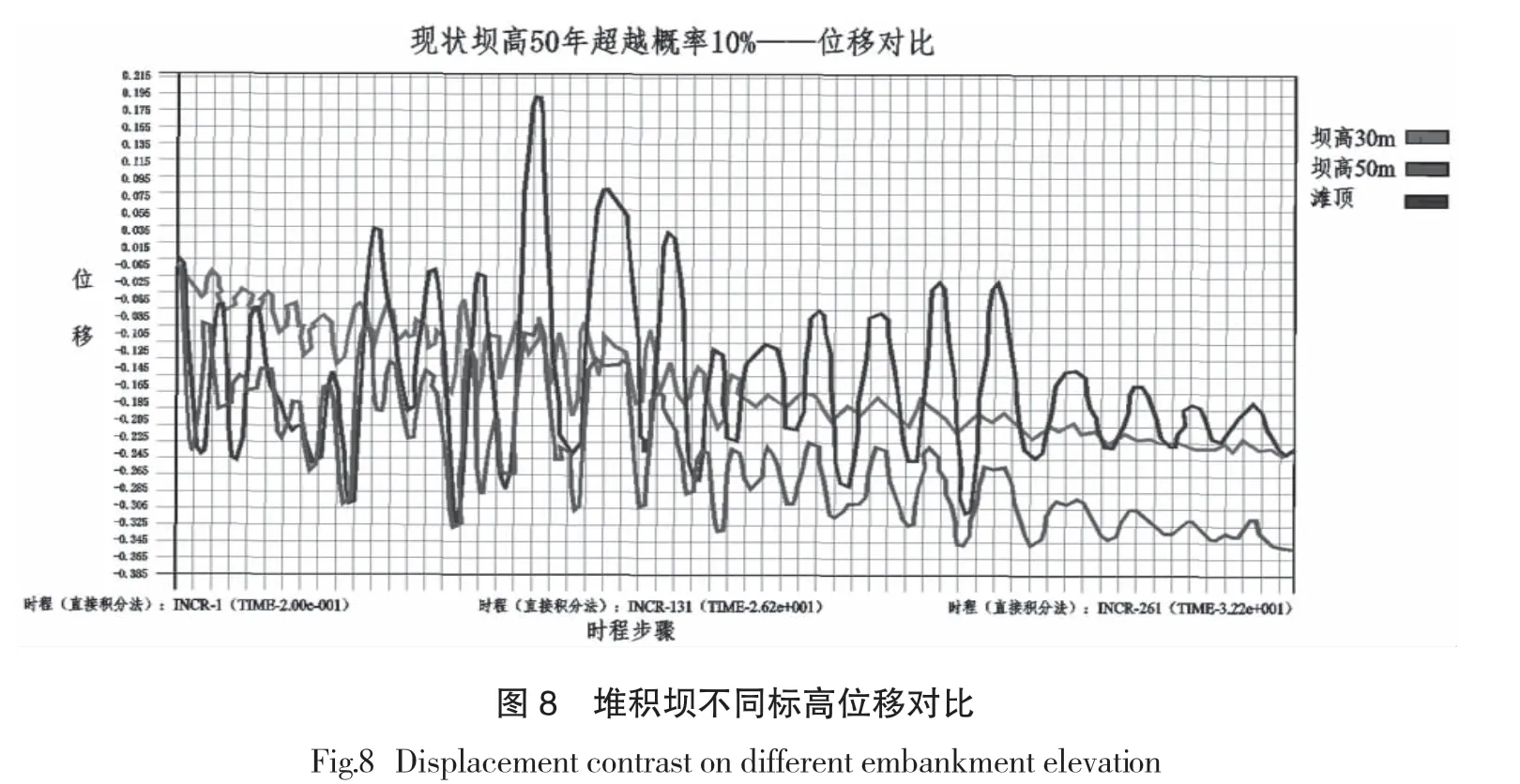
(1)标高30m 的坝坡结点在地震荷载作用下的最终永久变形(塑性变形)约为0.24m。
(3)滩顶标高结点在地震荷载作用下的最终永久变形(塑性变形)约为0.24m。受鞭梢效应影响,该点在地震荷载作用下一直在原位置左右振荡,位移较对称。由于竖向荷载小,因而塑性变形相对较小。
(4)在地震荷载作用下,坝体总高中部附近土层在地震荷载及上部土体的荷载综合作用下塑性变形较大,易发生土体失稳。初期坝上方一定范围内土体在初期坝的作用下塑性变形较小。
3.3.4 位移云图分析
图9为基本烈度水平地震荷载作用下的土体水平变形情况,可以看出:

(1)粘性边界在一定范围内对模型的计算结果有一定影响,但从标记出的初期坝下位移结果(0.004m)可知,模型边界已足够大,没有影响到重点计算区域的结果,能够满足要求。
(2)在此地震荷作用下,坝体坡面中上部的水平位移变形较大,易发生土体滑坡。
3.4 坝体地震稳定性分析
坝体地震稳定性计算采用时程+SRM法。SRM法即强度折减法,可以满足平衡力条件、协调条件、本构方程和边界条件的要求,较为真实地模拟边坡破坏形态及现场条件,得到边坡最小安全系数及边坡破坏性状的详细信息,此外破坏过程是自动完成的,不需假定破坏面。50 年超越概率10%和5%的安全系数时程计算结果如图10-11所示。
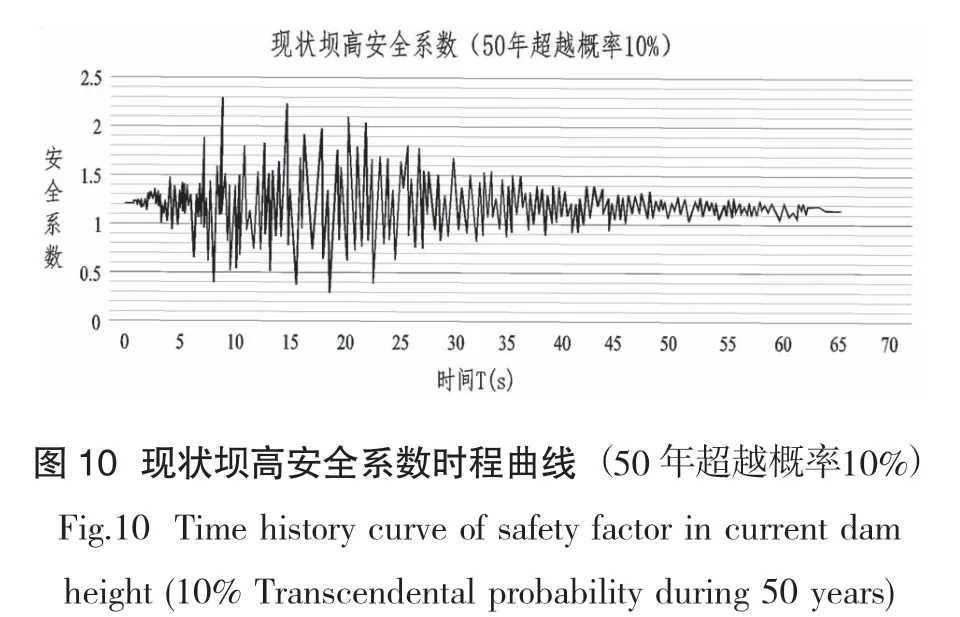

由图10-11可知,坝体在地震荷载作用下安全系数有较大波动,某些时刻安全系数小于0.5,出现小量计算不收敛时刻。从安全系数时程曲线可知,坝体的安全系数在1.2上下波动,虽然后期数值有减小的趋势,但坝体的稳定性系数大于1,坝体处于基本安全状态,但安全储备不足。
4 主要结论和建议
4.1 主要结论
(1)尾矿坝的地震响应与尾矿坝坝体的特征周期、地震波的特性有密切关系。相同坝体状态在输入不同特性的地震荷载作用时,尾矿坝的地震响应截然不同,有较大差异。
(2)坝体在地震荷载作用下均出现了不同程度的塑性变形,且塑性变形不断累加,影响坝体的整体稳定性。
(3)尾矿坝在现状坝高状态下,遇到与计算所用的2条地震波(50 年超越概率10%和5%)类似的地震荷载作用,坝体刚刚满足规范要求;若遇到罕遇地震的地震荷载作用时,将有失稳的风险。
(4)在地震荷载作用下,滩顶及靠近最高子坝一定范围内的下部地层有液化现象,对坝体的稳定性不利。
4.2 建议
(1)对现有初期坝进行加固,提高初期坝在坝整体稳定性方面的作用;对初期坝后浅层的透镜体及粘质粘土层采取改良、加固等技术措施。
(2)改善筑坝材料的力学性能,改进筑坝工艺;采取有效排渗措施降低坝体浸润线高度,从而改善土层的力学性能,减小地震液化范围。
(3)增大正常运营状态下的干滩长度,使坝后大范围内沉积尾矿粗颗粒,从而增大土层的渗透系数、改善坝体的自振特性和性能。
(4)确保在线监测设施可靠性,保证监测数据传输的及时准确,密切监控尾矿库安全状态。
