经验模态分解法在高频形变干扰分析中的应用

孔祥瑞，翟丽娜，李梦莹，张志宏，黄明威

（辽宁省地震局，辽宁 沈阳110034）

0 引言

形变观测是通过精密仪器，对地震前发生的与地震孕育和发生过程有关的构造运动、震前变形、同震形变、震后恢复等相关现象的观测。因此，形变观测产生的数据，极有可能蕴含着地震前的前兆信息。一般情况下，地震前兆观测数据中含有不同的周期成分有如下几种：（1）趋势变化，即不同变化的长期变化，时间尺度为几年，甚至几十年不等；（2）年周期变化，表现为各种因素的综合影响引起的，年变一般每年存在极大值、极小值；（3）固体潮变化，前兆观测资料含有的固体潮汐资料，整点值数据可以刻画固体潮变化；（4）各种随机因素引起的观测数值的随机变化，一般为短期［1-2］。

由于形变观测仪器在获取震前形变信号变化的同时，也会记录到人类生产、活动的干扰，以及观测自身系统的噪声影响所产生的干扰信号，这些都会使得观测数据具有非平稳性、非线性特征。随着数字化形变观测仪器大量投入观测，数据观测频率由小时值数据提高到分钟值数据，采样率大幅度提高。但与此同时，各种高频干扰信息如风扰、同震变化，使得观测仪器会记录到更多的干扰因素，为我们分析提取形变异常信息造成了一定的困难，因此排除这类干扰因素越发重要。传统的处理方法如FFT 或者小波变换的前提条件，都要求所处理的信号必须具有线性和平稳性的特征，因此客观上讲，传统的处理方法处理前兆资料具有一定的局限性［3］。

本文采用近年出现的经验模态分解模型（EmpiricalModeDecomposition，EMD）［4-6］，将形变观测信号经过EMD分解为一组不同尺度内在的、客观的固有模态函数（IntrinsicMode Function，IMF）。基于EMD的优良性能，本文首先利用EMD 模型对形变观测数据进行一定分解，在获得IMF 之后再把某些IMF 进行适当的组合，便可以构成特定意义下的低通、带通与高通自适应滤波器，然后进行数值仿真试验，最后处理形变观测资料，探索消除形变观测资料中的干扰因素。

1 基于经验模式分解的滤波原理与思路

1.1 经验模态分解与重组的基本原理介绍

经验模态分解方法（EMD）是将原始信号分解成若干固有模态函数（IMF），在这个过程中原始信号的各种频率的成分以不同固有模态函数的形式从原始时问信号中分解出来。其中固有模态函数满足：（1）整个数据中，零点数与极点数相等或至多相差1；（2）信号上任意一点，由局部极大值点确定的包络线和由局部极小值点确定的包络线的均值均为0。

IMF 求取的步骤如下：对一原始信号X（t），先求出这个序列的极大值点构成的上包络线和极小值点构成的下包络线的均值即为m，将原始信号X（t）减去包络均值m，得到一个新的数据序列h，即：

重复以上操作，直至h满足IMF 条件时，可将h视为第一个IMF，即：

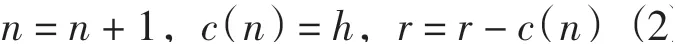
将r 视为新的X（t），重复以上步骤，即可依次获得IMF1、IMF2…最终获得分解结果：

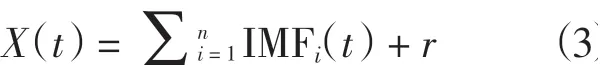
其中，X（t）为原始信号，IMF 代表固有模态函数，r 为残余函数，即剩余的趋势项部分。

基于以上分解获得的IMF 序列，我们可以完全进行重构，将IMF 序列按频率由高到低进行排列，将干扰所影响的优势频率进行剔除，从而进行高频干扰去除。

1.2 随机噪声信号经验模态分解与重构例子

通过对已知模拟信号进行EMD分解，是了解其效果最为简单的方法，为此设计包含随机噪声的已知信号，其中图1（a）基础函数为x=cos（2×π×0.5×t-π/2）；添加随机噪声参数为0.3倍符合标准正态分布的一维矩阵的函数图1（b），最终可以获得随机噪声的时间序列图1（c）。

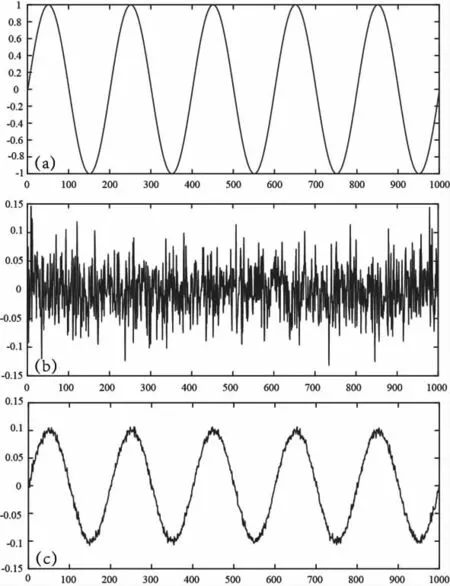
图1 随机噪声信号时序曲线Fig.1Sequentialcurvesof random noisesignal

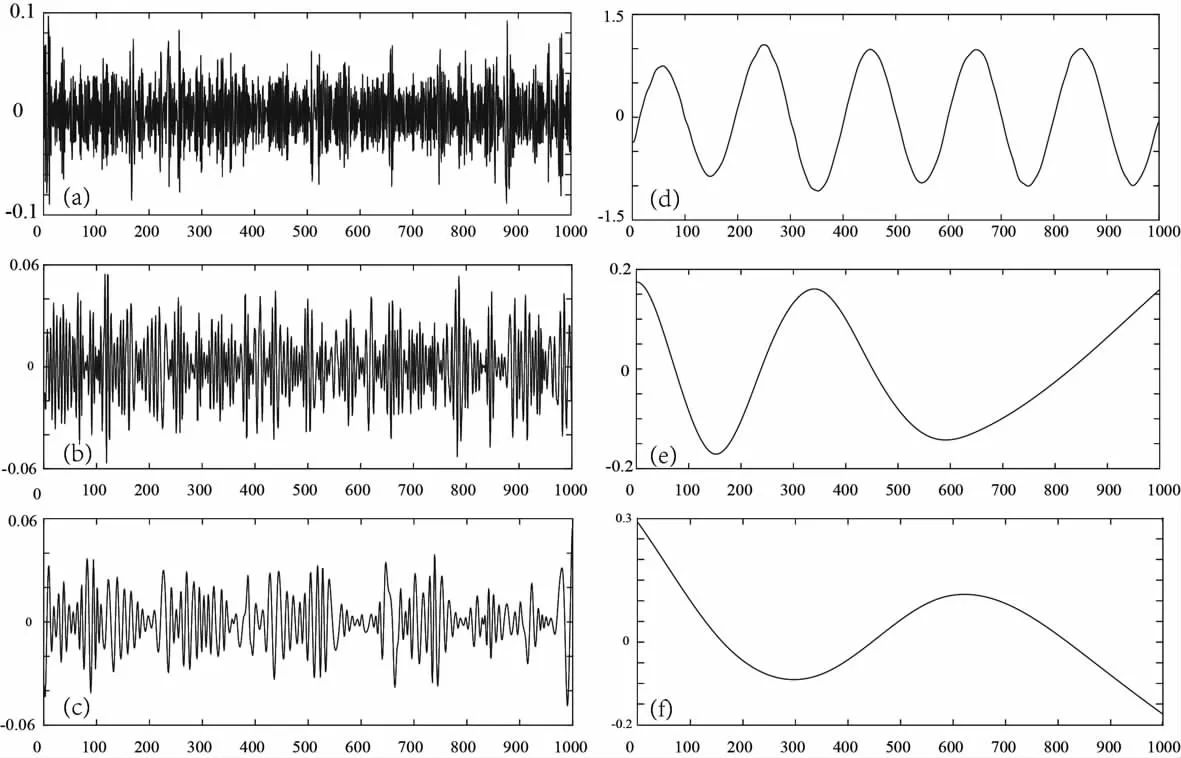
图2 随机噪声信号时序分解及结果曲线Fig.2 Sequencedecompositionandresult curvesof random noise signal

将含有随机噪声信号时序经由EMD 模型分解，可以获得由6重IMF 组成的重组滤波（图2），而我们可以将分解的6重信号进行叠加，可以获得原始噪声序列曲线（图1（c））。各个分量所对应的时频谱图像如图3所示，主频率从高到低依次排列，其中高频信息主要集中在前三个分量（a）、（b）、（c）上，所以干扰噪声也就集中在此部分，因此我们可以排除这些信号进行重组，这样我们既可以保持原曲线的形态，又可以剔除高频干扰信息。

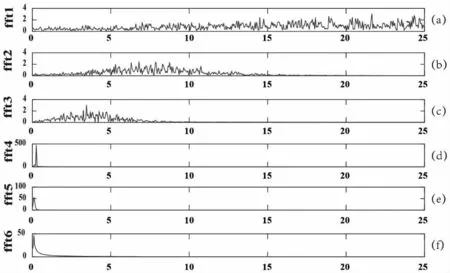
图3 各个IMF 对应时频谱图像Fig.3The variousIMF imagesof theseasonal spectrum

为了验证获得数据的有效性，我们可以将图2（a）、（b）、（c）进行叠加，与原噪声曲线所添加的噪声图1（b）进行相关性分析，分析所提取出的高频信息与添加的噪声的相关性，经过对比，其相关性系数达到0.930，基本满足提取高频信息的需求，使用此方法我们可以提取震前形变高频异常，或者在保存数据趋势变化的基础下，去除例如风扰等外界环境和仪器本身的高频信息，为分析预报提供帮助。

同样道理我们将图2（d）、2（e）、2（f）进行叠加，与未添加噪声的曲线图1（a）进行相关性分析，其相关性系数为0.999。此方法可以在保证趋势变化的基础上，对数据进行滤波，滤波的尺度我们可以自行掌控。由此可以说明信号经过合理的分解与重构，基本可以获得高频和低频信息，为进一步的数据分析提供帮助。

2 形变干扰信号在经验模式分解与重组中的应用

随着数字化观测仪器的普及，分钟值形变观测数据中高频干扰是经常出现的现象，例如风扰、降雨、同震等影响，这些干扰并不会影响数据的曲线形态，而是对数据产生高频干扰，这些干扰或是瞬时的，如同震；或是持续的，如风扰。我们对这类信号主要是去除高频信息，按上述的例子，只需将原始信号减去先剔除的高频信号即可，以丹东水管EW 分量为例，丹东水管倾斜自观测以来，数据一直良好，年变形态清晰，但该测项分量受风扰干扰尤为明显，具体体现为高频波动，尤其在每年的3—6月，风扰更加明显，本文选取2016年3—4 月份数据，在3月21日存在一次同震响应（图4）。

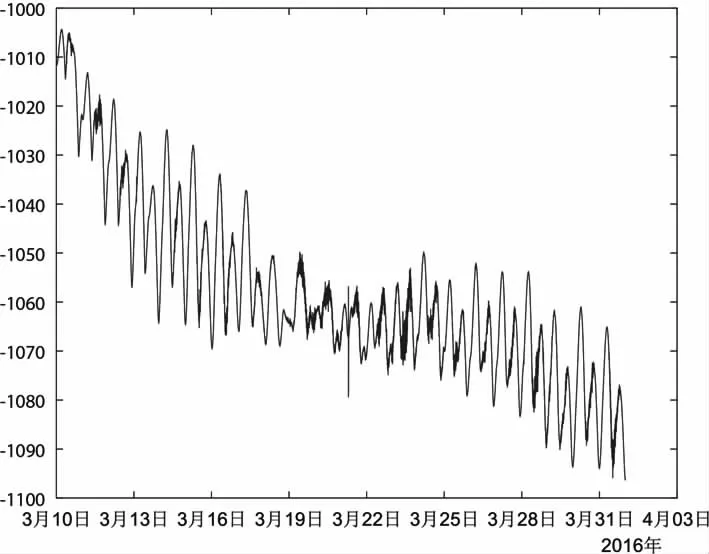
图4 丹东水管EW 分量观测曲线Fig.4The EW component observationcurveof Dandong water pipe

按照上述方法进行分解，可以获得不同频率的多个IMF 函数，本例子获得13阶IMF 函数，通过对分解出的各个阶IMF 函数分析，可发现大风扰动和同震的高频干扰信息主要集中在前六层IMF 函数，故将其前六层重新组合可获得高频干扰信息，因此我将前六层信息进行组合，获取干扰信息（图5），将其他剩余的IMF函数进行重新组合，便可获取去除高频干扰的观测曲线，为进一步的分析提供帮助（图6）。

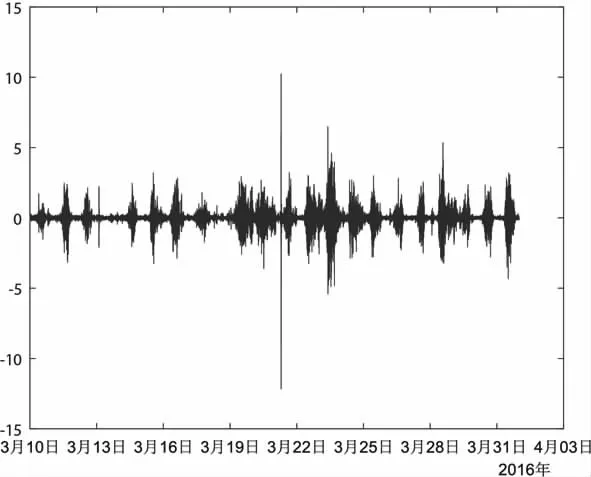
图5 丹东水管EW 分量高频干扰曲线Fig.5High frequency interferencecurve of EW component of Dandong water pipe

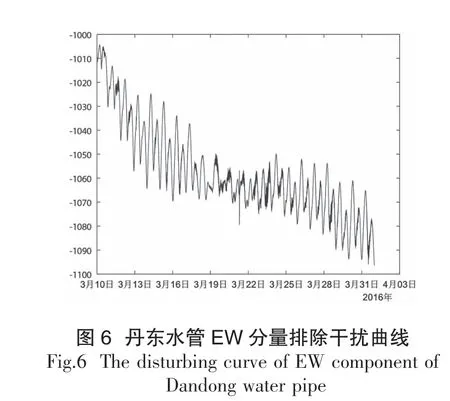
通过对丹东水管EW 分量的风扰高频干扰和同震响应的提取和去除，我们可以基本去除其影响信息，并且去除干扰后的函数也并没有因为滤波的因素而改变和影响本序列原有的信息，因此该方法尽可能的在保留固体潮等数据特征的基础上去除干扰，为数据进一步分析提供支持。

3 结束语

本文首先通过对EMD方法及原理进行简单介绍，然后对理想下的已知模拟信号进行人为加入噪声信息，用该方法进行实验，最后把EMD方法技术应用于形变信号处理领域之中。通过以上综合分析可得到如下结论：

（1）EMD分解中首先被提取出来的IMF 频率最高，第一个被EMD方法提取出来的IMF函数表示原信号的最高频率成分，再此之后每一层的信号频率逐渐降低，直到分解到最低频停止分解，每一个IMF 序列均稳定在一个频率之间，也正因此，每一个IMF 序列都具有一定的物理意义。并且该方法并没有对引号进行过多干预，保证信号的原本特性的真实性。

（2）通过对存在的典型大风干扰的丹东台水管观测时间序列进行EMD分解和IMF组合滤波，进一步表明基于EMD分解在形变信号处理时的方法与思路，并且通过对数据处理之后的形态来看，该方法最大幅度的保存了信号的原始信息，如固体潮变化。因此认为，该方法对形变信号的提取高频信息具有有效性和可靠性。