采用独立覆盖流形法分析精确几何描述的曲壳

,　,,　

(长江科学院 材料与结构研究所，武汉　430010)

1　研究背景

曲壳(也称为壳)不仅造型优美，而且是一种非常经济的承载结构，在工程中得到广泛应用。曲壳的力学分析，除了极少数的简单情况有解析解答外，绝大多数都采用以有限元法[1]为主的数值计算方式。

理论上，曲壳可以采用由控制方程建立积分弱形式的标准方式来建立数值分析表达式。然而，曲壳控制方程(包括平衡微分方程、物理方程和几何方程)的推导本身就比较复杂，涉及曲面微分几何的很多内容，而且基于不同假设会得到不同方程，因此鲜有直接应用曲壳控制方程形成数值计算过程的尝试[2]，仅有适用于特殊简化理论的扁壳单元等极少类型。

在有限元分析中，应用最多的是由平板单元拼接成曲壳的方式[1]。理论上，足够多的平板可以逼近连续曲面的精确几何形状，并模拟其真实的力学行为。这种几何精确性对曲壳非常重要，然而目前一般依赖人为判断，容易产生几何误差进而带来力学分析上的误差。即使对于平板单元本身而言，由薄板弯曲的4阶微分方程得到的积分弱形式，要求近似函数具有C1连续性，这一直以来都是研究难点和热点，直至现在还不断有新的研究成果，由此产生了各种协调的或非协调的甚至是基于多场分析的平板单元，但大都有各自的适用范围，给用户的选择造成困难。

采用实体计算的退化方式是另一种有效途径[2]。它应用壳体的Reissner-Mindlin假设，可以考虑横向剪切变形，而且近似函数只需要C0连续性，更重要的是，可以在有限单元的各边增加结点以模拟曲面几何。但其缺陷是容易出现剪切自锁和薄膜自锁，虽然可以通过减缩积分等方式进行处理，但可能带来矩阵的奇异性等其他问题。

近年来出现的等几何分析方法[3]，强调几何的精确性，适用于对几何要求很严的曲壳分析，但其基函数较为复杂，对复杂求解域的适应性不强，而且难以完全避免自锁等问题[4]。

我们在前期研究中基于独立覆盖流形法，采用二维实体分析方式，提出了直梁和曲梁的独立覆盖分析方法[5-6]。其中，只需借助随中面参数方程变化的局部坐标系，并考虑该坐标系的局部坐标以及方向余弦关于整体坐标的导数，就能实现精确几何描述下的曲梁分析。文献[6]给出常曲率的圆形曲梁和变曲率的椭圆形曲梁算例，验证了该方法的可行性。本文将此方法推广到三维板壳(包括三维曲壳和三维平板)分析，从而形成一整套梁板壳分析的新方法。

2　独立覆盖流形法简介

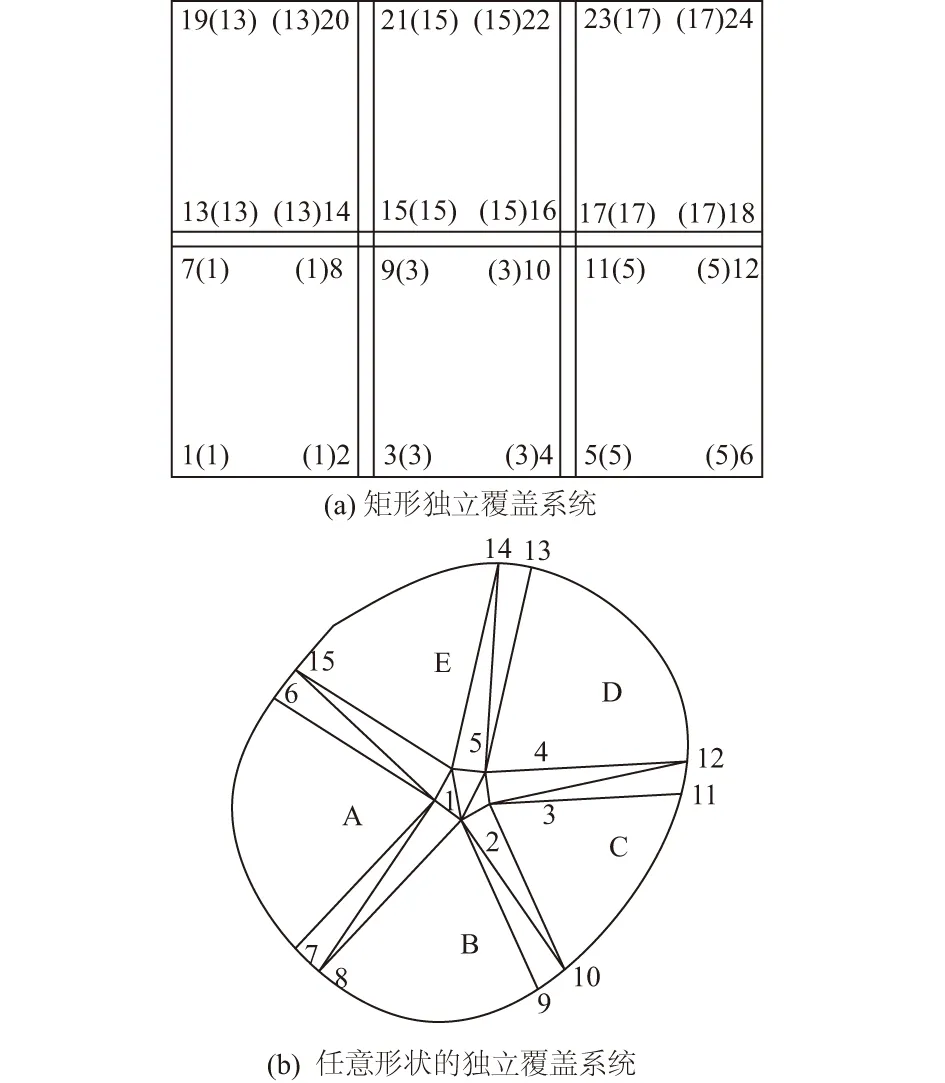
图1　独立覆盖及其条形连接Fig.1　Independent covers connected through strips

2012年，笔者在石根华博士的建议下，在流形法中首次引入“独立覆盖”[9-10]，即单位分解函数φi=1、近似函数V就是给定级数Vi的覆盖区域，独立覆盖之间为窄条形的覆盖重叠区域，其单位分解函数取为有限元的线性形函数以实现覆盖函数的线性过渡。每个覆盖包含一个独立覆盖及其周边的条形重叠区域。如图1(a)所示，首先研究了矩形独立覆盖系统，图中的大矩形为独立覆盖；2013年提出任意形状的独立覆盖[11]，如图1(b)所示，A，B，C，D，E这5个任意形状的独立覆盖用条形连接，为方便计算，不规则的条形以及条形交叉处都划分为三角形，这样，覆盖的划分不仅能适应求解域的物理边界，还能严格施加本质边界条件[12]。

2015年笔者在文献[13]中正式命名“基于独立覆盖的数值流形方法”，简称“独立覆盖流形法”，其中，独立覆盖和条形都是基本的计算单元(称为覆盖网格)，但强调独立覆盖的主体作用。独立覆盖流形法的收敛性是在各覆盖区域内采用的完备级数(如多项式级数)逼近真实解的基础上建立的，不仅包括物理场本身的收敛，而且包括高阶导数的收敛。覆盖网格具有任意形状、任意连接、任意加密的特性。

3　独立覆盖上的曲壳覆盖函数

覆盖函数的多样性是独立覆盖流形法的显著优势。可以通过选择覆盖函数以反映物理场的局部特性或整体特性，前者如文献[10]的裂纹分析，在裂纹尖端附近选择解析级数作为覆盖函数从而加快收敛，后者在文献[5]、文献[6]以及本文所讨论的梁板壳分析中，选择多项式覆盖函数的合适形式以反映梁板壳的整体变形特征。

如图2所示的整体直角坐标系x-y-z下，在第i个独立覆盖中，中面坐标(x0i,y0i,z0i)由壳体曲面参数方程描述，以(x0i,y0i,z0i)为原点建立沿中面变化的局部正交坐标系xi-yi-zi，其中xi和yi沿中面内的曲线坐标方向(切向)，zi沿厚度方向(即中面的法向)。xi和yi考虑为曲线坐标，zi表示壳体上的点到中面的距离。若中面由多个曲面连接而成，相同曲面的覆盖可以合并使用同一曲面定义的曲线坐标。

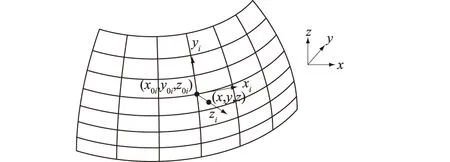
图2　整体直角坐标系下的曲壳及其局部坐标Fig.2　A curved shell and its local coordinates underthe global rectangular coordinate system

值得注意的是，一般的多项式级数表达都是关于整体坐标系的，本文将其推广到随中面变化的局部坐标系下的多项式级数表达。将壳体作为三维实体考虑，设局部坐标xi，yi，zi方向的位移分别为ui,vi,wi，参考文献[1]，根据壳体的Reissner-Mindlin假设，设壳体上的各点在局部坐标下的位移为

(1)

式中：壳体中面位移仅仅随曲线坐标xi和yi变化，与zi没有关系，因此3个方向的中面位移分别设为f1(xi,yi),f2(xi,yi),f3(xi,yi)；沿厚度zi方向的应变可忽略，因而对于固定了xi和yi坐标的壳体上的任一点，有wi(xi,yi)=f3(xi,yi)；再根据平截面假设，用zif4(xi,yi)和zif5(xi,yi)分别描述xi向和yi向纤维沿厚度方向呈线性变化的伸长量(分别相对于中面位移f1(xi,yi)和f2(xi,yi))，其中f4(xi,yi)和f5(xi,yi)分别表示独立定义的随中面坐标变化的截面转角θxi和θyi。

关于局部坐标的完全多项式为

(2)

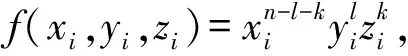
如图3所示的多项式排序，显示了从0阶到2阶的完全多项式。应用式(2)构造的局部近似函数，采用实体计算模式，只需考虑虚线左侧的各项，而使虚线右侧的各项不参与计算，就能得到式(1)，实现壳体的Reissner-Mindlin假设。另外，当3个方向的位移取同阶多项式时，wi=f3(xi,yi)比θxi=f4(xi,yi)

(a)xi和yi方向

(b)zi方向

图3多项式排列
Fig.3Polynomialorder

和θyi=f5(xi,yi)高1阶，从而避免了剪切自锁问题。在xi和yi方向上，定义了关于xi和yi的完全多项式以充分反映薄膜变形，从式(1)可以看出，纯弯模式在中面(zi=0)处不会产生附加的薄膜变形，因此避免了薄膜自锁问题。

4　曲壳分析公式

如图2所示，在第i个独立覆盖内，引入转换矩阵Li(各项为局部坐标轴的方向余弦)，将曲壳各点的局部位移转换到整体坐标系下的位移，即

(3)

式中：cosαxi，cosβxi，cosγxi分别是xi轴关于整体坐标x，y，z的方向余弦，其他依此类推。

如果网格在xi-yi上投影为矩形单元，可以采用矩形有限单元的形函数作为单位分解函数，并应用强制约束关系[9-10]实现独立覆盖和条形。比如，在图1(a)中将结点2、结点7、结点8的所有自由度约束到结点1，实现独立覆盖1；将结点4、结点9、结点10约束到结点3，实现独立覆盖3；两者之间的条形为线性连接。

对于任意形状覆盖，根据文献[11]，在图1(b)的三角形单元1-6-7中，将结点6、结点7约束到结点1，实现独立覆盖A；独立覆盖B类似；A和B之间的条形由2个三角形单元组成，由结点7约束到结点1，结点8约束到结点2，实现A和B之间的线性过渡。因此所有的计算单元(包括独立覆盖及条形)都可以采用同样的计算公式(暂不考虑强制约束)，不失一般性，以下公式都在有限单元内采用高阶的常规流形法公式进行推导，位移表示为

(4)

式中：对于三角形单元，m=3；对于矩形单元，m=4；Wi对应于第i个覆盖(结点)的单位分解函数，取为二维有限单元的形函数，可由单元内各点在xi-yi上的投影坐标确定[1]。设

(5)

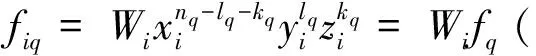
(6)

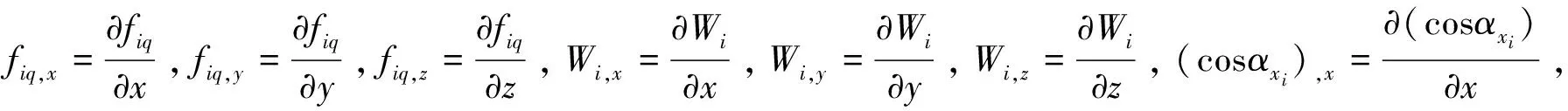
(7)

其中,

(8)

fiq,y和fiq,z依此类推。

其中：

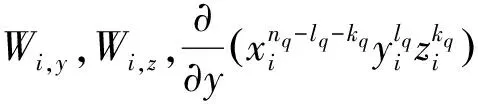
式(7)第3个等号后面的第2项矩阵为局部坐标系的方向余弦关于整体坐标的导数计算，对于平板分析，由于方向余弦不变，因此无需考虑。

如图2所示，考虑zi轴上的壳体点(x,y,z)与中面点(x0i,y0i,z0i)构成的矢量，由简单的几何关系，得到壳体点的整体直角坐标与局部坐标的转换公式为

(10)

以式(10)再结合中面点(x0i,y0i,z0i)的曲面参数方程表达式，就可以将式(9)、式(8)乃至式(7)具体地计算出来，见下节中关于几何的具体计算步骤。

按最小势能原理推导单元刚度矩阵的子矩阵为

(11)

式中：Ω为计算单元的三维空间区域；i=1,2,…,m；j=1,2,…,m；q，t分别表示对第i和第j覆盖所对应的多项式覆盖函数中参与计算的所有项进行循环；D为空间弹性矩阵[1]。

集中荷载和分布荷载的子向量分别为：

(12)

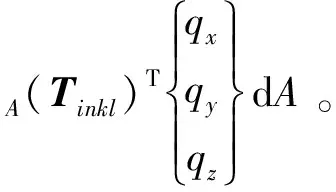
(13)

式中：Fx,Fy,Fz分别为整体坐标3个方向的集中荷载；qx，qy，qz为分布荷载集度；A为分布荷载作用面积。

将上述单元刚度矩阵和单元荷载向量分别组集成整体刚度矩阵和整体荷载向量，然后参考文献[12]加上边界条件，就可以求解线性方程组得到多项式的系数，再根据式(4)和式(7)得到整体坐标系下的位移和应变。

5　积分方式及几何计算公式

本文仅考虑中面为一个曲面的情况，只定义一个随中面变化的正交局部坐标系。设中面的曲面参数方程为

(14)

将曲线坐标设为xi=ξ，yi=η，厚度方向zi=r，且在中面处r=0，则局部坐标表示为ξ-η-r。另外，αxi，βxi，γxi等分别用αx，βx，γx等表示。

∭ΩF[x(ξ,η,r),y(ξ,η,r),z(ξ,η,r)]dxdydz=

∭ΩF(ξ,η,r)h1h2h3dξdηdr。

(15)

式中：h1，h2，h3分别为3个局部坐标的拉梅系数，其中，在zi坐标轴上用r表示点到中面的距离，则h3=1。

令

(16)

式中r1(ξ,η)和r2(ξ,η)分别表示沿厚度方向积分的下限和上限(即-h/2到h/2，h为厚度，可以考虑h随ξ-η的变化)。将单元各边与单元形心相连形成三角形，采用Hammer数值积分[1]计算，即

(17)

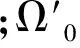
综上所述，只需在积分点(包括在中面投影区域内和沿厚度方向)上计算被积函数值，再乘以相应的积分权值，就可以得到式(11)的刚度子矩阵。式(13)关于分布荷载的计算类似。

从新媒体在2016年美国总统大选及在特朗普阵营发挥的作用看，特朗普现象不应仅解读为民粹主义本身的再度崛起，而是民粹主义结合新媒体取得成功的例证。民粹主义的出现既有历史文化原因亦有受政治机会主义者煽动利用因素。如今，民粹随经济危机再度回归，公众不再跟随精英的观点成为2016年大选的背景（Gelman&Azari 2017），这一态势为特朗普成功利用并进一步塑造。民粹和民主的界限本身也颇为微妙，“服务人民”即便未曾出自每个美国总统竞选者之口，也毫无疑问是不可否认的命题。呼唤“多数人的统治”本身既是政治理念又是政治策略，这赋予民粹主义在美国政治生态中顽强的生命力。

在关于几何的具体计算过程中，关键是局部坐标和方向余弦关于整体坐标的导数计算，以下给出计算步骤：

(1)根据中面的曲面参数方程，得到xi轴、yi轴、zi轴的基向量分别为(式(18)和式(19)暂用x，y，z分别代替xi，yi，zi：x=x0i(ξ,η);y=y0i(ξ,η);z=z0i(ξ,η)):

(18)

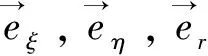
(2)由式(18)求出积分点(ξj,ηj)处xi轴、yi轴、zi轴关于整体坐标的方向余弦为：

(19)

其中，

L=(y,ξz,η-z,ξy,η)2+(z,ξx,η-x,ξz,η)2+(x,ξy,η-y,ξx,η)2

(3)根据式(10)可得

(20)

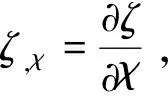
对于确定的某种曲面，以上推导公式的过程是一次性的。

6　球面壳算例

如图4(a)所示的球坐标系，按第5节的4个步骤计算如下：

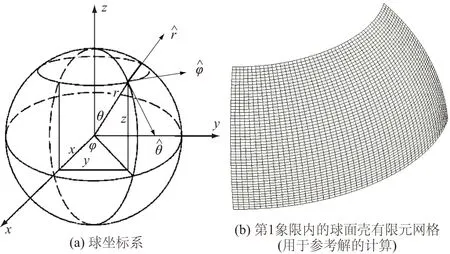
图4　球坐标及第1象限内的球面壳有限元网格Fig.4　Spherical coordinates and a sphericalshell in the first quadrant

(1)中面的曲面参数方程为

式中：(x0,y0,z0)为球心坐标；R为半径；ξ=θ；η=φ。因此有：

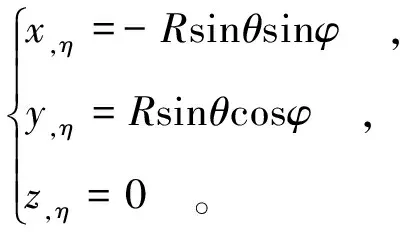
然后得到拉梅系数h1=R，h2=Rsinθ。

(2)αx，βx，γx，αy，βy，γy，αz，βz，γz的余弦值可表示为：

(3)由式(10)和球壳中面参数方程得

将上式对x求导，解方程求出：

同理分别对y和z求导，得到：

(4)将各方向余弦分别对x求导，得到

-ξ,xsinθcosφ-η,xcosθsinφ。

其他方向余弦的导数依此类推。

对y,z求导，只需将上式中的x改为y或者z。

计算如图4(a)所示的第1象限内的球面壳，半径R=1 m，θ=π/4～π/2，φ=0～π/2。壳体厚度为0.01 m，左端(φ=0)和右端(φ=π/2)为固支约束，球面壳上表面承受法向均布压力P=10 kPa。弹性模量E=106kPa，泊松比μ=0。图4(b)显示了用于计算球面壳参考解的有限元细密网格，由5 000个平板单元拼接而成。

如图5所示，在φ-θ的投影平面上，流形法计算分别采用3种矩形有限元网格：网格1——只用1个独立覆盖；网格2——5×3(φ向×θ向)个独立覆盖；网格3——9×5个独立覆盖。采用文献[12]的边界条件施加方法：在网格1的左、右两端各增加1个条形，与固定约束的结点相连；在网格2和网格3的左、右端各个独立覆盖中，直接设定覆盖函数使之事先满足边界条件。

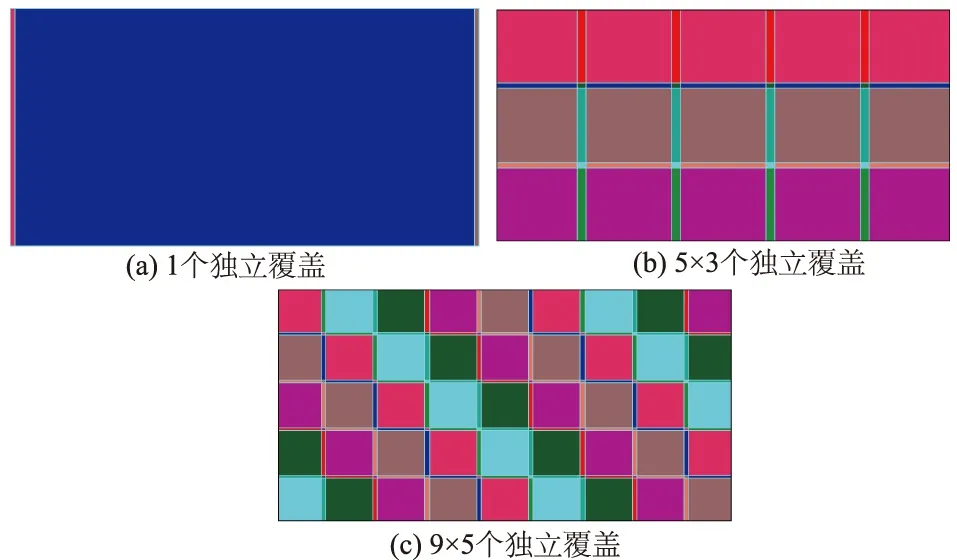
图5　φ-θ投影平面上的覆盖网格Fig.5　Cover meshes in φ-θ projection plane

计算得到的各方向最大位移见图6，出现在(θ=π/2，φ=π/4)点处：当采用网格1(1个独立覆盖)时，必须取到9阶多项式覆盖函数时才能收敛，x向(由对称性，x向和y向相等)和z向最大位移分别为0.583和0.275(单位10-2m，下同)；网格2(5×3个独立覆盖)，5阶多项式的结果为0.579和0.272，6阶多项式为0.581和0.273；网格3(9×5个独立覆盖)，4阶多项式的结果为0.580和0.272，5阶多项式为0.581和0.273。而图4(b)细密网格的有限元参考解为0.581和0.274，与3种网格下的收敛解几乎一致。可见，不管采用粗网格配以较高阶次的多项式，还是采用细网格配以较低阶次的多项式，都有很好的收敛性。在控制好计算误差的前提下，可采用升阶和加密覆盖的2种方式来提高精度。

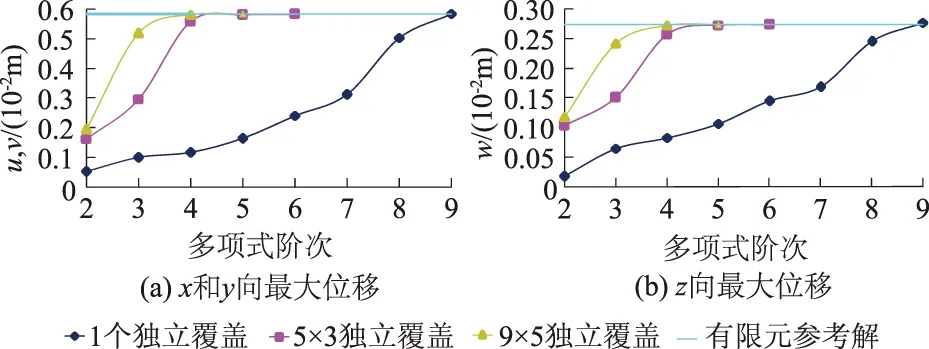
图6　球面壳的最大位移Fig.6　Maximum displacements of the spherical shell

关于ξ-η平面上的三角形Hammer积分点数，对网格1的试算表明：4阶及以下的多项式覆盖函数情况可用7点积分；5阶和6阶为12点积分；7阶及以上至少需16点积分。因此，较高的多项式阶次虽然可用较少的自由度达成收敛，但刚度矩阵积分的计算量也很大。

当去掉式(7)等号右边的第2项矩阵，就可以进行平板计算。如图5所示的平板，x=0～π/2(单位:m)，y=π/4～π/2(单位:m)，同样的左、右两端固支约束和均布荷载情况下，网格1(1个独立覆盖)采用4阶多项式覆盖函数计算得到中点处的最大位移为1.903(单位10-2m，下同)，与细密网格的有限元解相同。若再考虑上、下端面的固支约束，则6阶多项式计算得到中点处的最大位移为0.115 6；网格3(9×5个独立覆盖)采用4阶多项式得到的最大位移为0.115 8；而细密网格的有限元参考解同样为0.115 8。可见，三维平板计算也有很好的收敛性。

值得注意的是，当采用1个独立覆盖时，单元最大边长与截面厚度之比超过150∶1，但未出现有限元法基于实体退化方式求解薄板壳时的自锁现象。

从图3的多项式选择来看，目前采用的方式是在某一阶次的完全多项式中去除关于zi的二次以上的高阶项。事实上，在以弯曲为主的板壳分析中，可以减少图3(a)中用于模拟薄膜变形的关于xi和yi的多项式阶次，比如上面的平板算例属于纯弯变形，可以将关于xi和yi的多项式完全去掉，使自由度数大幅下降。进一步可以参考文献[5]，基于物理场导数的收敛性，考虑截面转角θxi=∂wi/∂xi和θyi=∂wi/∂yi以模拟薄板的Kirchhoff-Love假设，从而再去掉图3(a)中关于zi的自由度。

限于研究时间较短，本文仅给出了常曲率的球面壳算例，未给出变曲率的曲壳算例。但从前文的理论推导，以及文献[6]给出的椭圆形曲梁算例来看，本文方法应用于变曲率的曲壳分析也无问题。另外，对于形状更为复杂的曲壳，可采用任意形状的独立覆盖。

7　结　语

本文采用独立覆盖流形法，在前期研究的关于直梁和曲梁的独立覆盖分析方法基础上，只需借助随中面参数方程变化的局部坐标系，并考虑该坐标系的局部坐标以及方向余弦关于整体坐标的导数，就能实现精确几何描述下的曲壳分析，而忽略坐标系的变化即可分析平板。

文献[5]的直梁、文献[6]的曲梁，以及本文的曲壳和平板分析，初步构成了一套基于独立覆盖流形法的梁板壳分析新方法。其特点是：

(1)完全采用实体分析模式，只需使多项式覆盖函数中的某些项不参与计算，就能模拟梁板壳变形的基本假设，从而避免了推导梁板壳控制方程以及数值分析公式的过程，特别对于曲梁和曲壳而言，该过程的复杂性体现在应用曲面微分几何推导不同假设下的控制方程，以及由积分弱形式推导数值计算的离散公式。另外，与实体单元的连接也无需特殊处理。

(2)不管是模拟细长的Euler-Bernoulli梁或薄板的Kirchhoff-Love假设，还是考虑横向剪切的Timoshenko梁或Reissner-Mindlin板壳假设，都仅要求近似函数的C0连续性，其中，前者需要考虑独立覆盖流形法的导数收敛性(薄板壳的相关公式及算例将在后续给出)。

(3)在数值计算的稳定性方面，虽然是实体分析模式，但不存在有限元实体计算中由于厚度远小于其他尺度而导致的数值病态，也无任何自锁现象。

(4)在实现几何保形性方面，避免了通常由直梁或平板单元构造曲梁或曲壳所造成的几何误差。这是除了等几何分析方法之外的另一途径，与之相比，本文方法具有多项式基函数相对简单、严格施加本质边界条件、完全消除自锁、覆盖加密方便等优点。

因此目前看来，这种新方法可以解决现有梁板壳分析存在的主要基础性问题。究其原因，以有限元法的自锁问题为例，有限元法基于插值方式构造近似函数，当采用实体退化方式分析梁板壳时，有限单元的插值函数并不是总能够描述正确的弯曲变形[2]：剪切自锁源于在纯弯模式下产生了伪横向剪切；薄膜自锁也是在纯弯模式下不能表达中面的无伸缩变形。而独立覆盖流形法是基于分区(覆盖)的直接逼近方法，所选用的多项式函数能够准确地表达梁板壳的弯曲变形和薄膜变形。

当然，目前还未就新方法的计算效率进行分析比较。新方法可以采用粗网格配以高阶覆盖函数，或者细网格配以较低阶的覆盖函数，甚至是结合独立覆盖流形法的精度分析实现覆盖任意加密的自适应计算，需要研究哪种方式(或自适应途径)的计算量更小，并通过优化算法进一步减少计算量。最近，笔者已完成了母线为曲线描述的旋转壳分析，正在考虑中面为不同曲线的连接；下一步要通过更多算例探讨新方法对各种梁板壳(包括三维曲梁)分析的适应性；将来进行梁板壳大位移的几何非线性分析，材料非线性分析，以及动力分析等。

致谢:感谢石根华博士的指导！

参考文献：

[1]ZIENKIEWICZ O C , TAYLOR R L. 有限元方法[M].5版. 庄茁，岑松,译. 北京: 清华大学出版社, 2006.

[2]BELYTSCHKO T, LIU W K, MORAN B.连续体和结构的非线性有限元 [M]．庄茁,译．北京：清华大学出版社，2002.

[3]HUGHES T J R，COTTRELL J A，BAZILEVS Y. Isogeometric Analysis：CAD，Finite Elements，NURBS，Exact Geometry and Mesh Refinement[J]. Computer Methods in Applied Mechanics and Engineering，2005,194(39/40/41)：4135-4195.

[4]李新康. 层合结构等几何分析研究[D]. 杭州：浙江大学，2015.

[5]苏海东，颉志强. 梁的独立覆盖分析方法[J]. 长江科学院院报, 2018,35(4):143-150.

[6]苏海东，周朝，颉志强. 基于精确几何的曲梁分析新方法[J]. 长江科学院院报, 2018,35(4):151-157,166.

[7]SHI G H. Manifold Method of Material Analysis[C]∥U.S. Army Research Office. Transactions of the Ninth Army Conference on Applied Mathematics and Computing, Minneapolis, Minnesota, U.S.A., June 18-21, 1991: 51-76.

[8]BABUSKA I,MELENK J M.The Partition of Unity Method[J]. International Journal for Numerical Methods in Engineering, 2015, 40(4):727-758.

[9]祁勇峰, 苏海东, 崔建华．部分重叠覆盖的数值流形方法初步研究[J].长江科学院院报, 2013,30(1):65-70.

[10] SU Hai-dong, QI Yong-feng, GONG Ya-qi,etal. Preliminary Research of Numerical Manifold Method Based on Partly Overlapping Rectangular Covers[C]∥DDA Commission of International Society for Rock Mechanics. Proceedings of the 11th International Conference on Analysis of Discontinuous Deformation (ICADD11), Fukuoka, Japan, August 27-29, 2013, London: Taylor & Francis Group, 2013: 341-347.

[11] 苏海东, 祁勇峰, 龚亚琦, 等. 任意形状覆盖的数值流形方法初步研究[J]. 长江科学院院报, 2013, 30(12): 91-96.

[12] 苏海东，颉志强．独立覆盖流形法的本质边界条件施加方法[J]. 长江科学院院报, 2017,34(12)：140-146.

[13] 苏海东，颉志强，龚亚琦, 等．基于独立覆盖的流形法收敛性及覆盖网格特性[J]. 长江科学院院报，2016, 33(2)：131-136.