双向内外管差压流量计参数优化与数值模拟

王太飞，孟　江，吉　鹏

(中北大学机械工程学院，山西 太原 030051)

0　引言

流量仪表技术在19世纪中叶到20世纪迅速发展。人类社会对流量测量的需求加快了流量仪表的更新换代[1]。直到近几十年，新材料和新技术的出现，使该行业实现了跨越式发展。在新型流量计层出不穷的时代，传统的差压式流量计仍占有一席之地。差压式流量计是目前在工业测量中应用较为广泛的流量仪表之一[2]。

对于近几年流行的V锥差压流量计，其优点是要求直管段较短、抗脏污等。但是V锥差压流量计难以兼顾较高的精确度和较低的压力损失，因此其并不是能源监测流量仪表的最佳选择。为了减少测量能耗及保证精确测量，对差压流量计进行了改进，如设计了内外管差压流量计[3]。内外管差压流量计能够在不改变总流通面积的前提下，在同一截面上获得差压，对管道内流体的流型影响较小，消除了节流件前后摩阻压降对差压信号的影响，达到了节能的效果；在相同的流量下，其获得的差压远大于传统差压式流量计，提高了信号的灵敏度；其节流方式对流体的扰动比传统流量计小，提高了差压信号的稳定性[4-6]。

虽然对内外管差压流量计的结构设计已有一些研究和优化，但仍存在一些问题。如文献[7]和文献[8]，虽然都获得了结构优化结果，并能有效地进行流量测量，但在结构相似的内外管流量计中流体方向相反，且取压位置分别为节流件的入口和出口处。为提高内外管差压流量计的实用性，解决内外管流量计在测量过程中流体流动方向和取压口的争议，设计了双向内外管压差流量计。该流量计可以不考虑流体流动方向，实现盲插安装，且取压口处信号更加稳定，为实际应用提供了便利。此外，对内外管差压流量计的结构优化通常是选择几个数据模型进行对比，以选择最优模型。为了得到准确的结构模型，本文利用二次回归正交组合设计的试验方法，并结合已有的模型数据，进行双向内外管差压流量计主要参数优化，得到确切的结构尺寸，为双向内外管差压流量计的进一步研究提供参考。

1　理论基础

1.1　工作原理

双向内外管差压流量计与一般的差压流量计原理相似，主要差异就是内外管取压差。双向内外管差压流量计结构如图1所示。其通过在流道2和流道1中取压差来进行流量测量。

流体流过双向内外管差压流量计节流件时(可不考虑流体流动方向，以图1中流体方向为例进行测量原理说明)，流体于截面Ⅰ被流道1和流道2分开。流体流至截面Ⅱ前，流道1对流体进行压缩节流，使流体流速增大，压力减小；流道2中流体扩散，使流体流速降低，压力增大。流体在截面Ⅱ直管段流速和压力都趋于稳定，并于截面Ⅱ处取压差。流体流至截面Ⅲ时，流道1中流体扩散，使流体流速降低；流道2中流体被压缩节流，使流体流速增大，压力减小，最后汇于主管道。

图1　双向内外管差压流量计结构图Fig.1　Structure of differential pressure flowmeter with　two-way internal and external tubes

流道1、流道2的连续方程为：

A11v11=A12v12=A13v13

(1)

A21v21=A22v22=A23v23

(2)

因为双向内外管节流件为对称结构，所以流体在流经截面Ⅰ、Ⅲ时，内外管的流体瞬时流速和压力相等。由此可得双向内外管差压流量计在3个截面处的伯努利方程：

(3)

(4)

当流体流经节流件时，由于节流件的长度短、扩散角小、水头损失小，通常会忽略水头损失。则：

z1=z2=z3

(5)

由此可得出流体流入节流件前的流速：

(6)

考虑到流体的黏度以及安装的支架对流场的影响，定义流出系数C。则流速可表示为：

(7)

式中：C为流出系数(一般为试验标定)。

不可压缩流体的体积流量可表示为：

(8)

式中：A为流道总截面积。

传统差压流量计体积流量的测量公式为：

(9)

可得双向内外管差压流量计的理论等效直径比为：

(10)

压差信号和压力损失是差压流量计的两个重要参数，其决定了流量计性能的优劣，是流量计设计过程中需重点考虑的因素。对于双向内外管差压流量计而言，内外管压差越大、前后压差越小，则压差信号越强、压力损失越小、性能越优越。为衡量双向内外管差压流量计的性能，选择引入压损比φ作为衡量标准，即：

(11)

式中：ΔP内外为内外管压差信号；ΔP前后为节流件前后永久压损。

在双向内外管差压流量计结构参数优化和不同差压流量计的性能对比中，压损比φ越大，流量计性能越好，越能满足工业生产的需要。

1.2　结构优化

本文采用二次正交回归组合设计的试验方法，利用二次正交回归表设计9组异径模型。然后，利用Fluent软件进行双向内外管差压流量计的模型建立和数值模拟仿真。依据仿真所得的压损比，建立回归方程，对试验结果进行优化。

2　模型仿真与回归分析

依据对内外管差压流量计以及喷射泵扩散角的优化研究[8-10]，选取外管道内径D为27.2 mm、节流件扩散角θ为7°。为更直观地显示双向内外管差压流量计的具体结构尺寸并有效屏蔽不合理的模型结构，选定节流件大径8≤d2≤23.2 mm、小径和大径之比0.4≤k≤0.8，并通过这2个因素确定双向内外管差压流量计的基本结构。

设定d2、k，建立正交组合试验方案。通过Fluent软件，依据试验方案建模、仿真并计算得到压损比，建立二元二次正交回归组合设计表，并根据试验结果建立回归方程；然后对偏回归系数进行显著性检验，证明需要建立的回归方程以及各偏回归系数都能够达到显著水平；最后根据极值条件，确定最大压损比下d2和k的值，得到压差信号灵敏、稳定的双向内外管差压流量计的结构。

模型建立后，采取自动网格划分。仿真条件设置如下：流体介质为水，为不可压缩流体；工况的温度为常温20 ℃；依据d2、k建立正交组合试验方案，并进行结构参数设置；管路水平放置，方向设置与图1方向一致；入口速度为 1 m/s、3 m/s。仿真得到的压损比为正交回归表中的φ值，需再进行回归分析与显著性检验。

根据临界雷诺数，判定管内为湍流状态，仿真模型选择2阶标准模式的湍流模型。将管路流场仿真的入口边界条件设为速度入口，并在速度入口的湍流参数设置中选择湍流强度和水力直径。其中：湍流强度为I=0.16(Re)-1/8，Re为水的雷诺数。出口条件选择流出出口，其他参数同入口条件一致，壁面条件设置为墙壁，并采用比较适合解决稳态问题的半隐式压力耦合方程组(semi-smplicit methool for pressure linked equations,SIMPLE)算法。在Fluent的后处理中，根据面积得到前后两点和内外管取压口四点处的压力，求得压损，并应用正交回归组合的试验方法进行优化计算。

取d2、k为正交回归组合设计中的两个因素，故因素数m=2，去零水平试验次数m0=1，星号臂长γ=1。由此可得该试验的因素水平编码表，如表1所示。

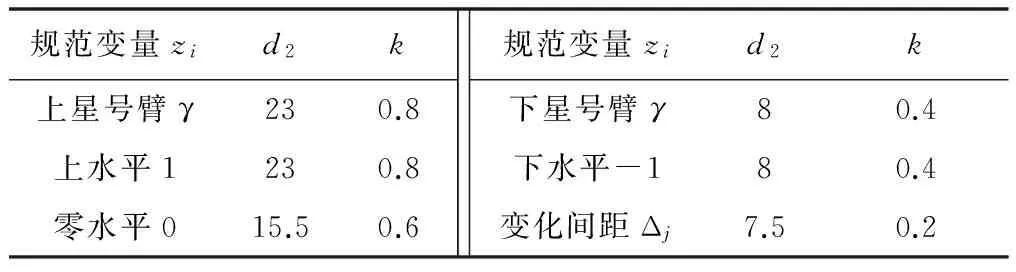
表1　因素水平编码表Tab.1　Factor levels coding

在Fluent中建立相应的仿真模型，并通过改变d2、k的值，共设计9组试验。在仿真的后处理中计算出相应的压损比，并记录在如表2所示的二元二次回归正交组合设计计算表中。表2中：z1与z2分别是d2与k的编码值。

表2　二元二次回归正交组合设计计算表Tab.2　Calculation table for binary quadratic regression orthogonal design

设定入口速度为1 m/s、3 m/s，在双向内外管流量计的入口、出口和节流件管中、管外设置4个取压点，依据式(11)求解出对应模型的压损比；利用回归分析，计算出9组模型的回归方程；根据极值必要条件，求解出最大压损比下对应的d2、k(节流件大径值、节流件小径与大径比的值)，由此得出最优模型。

当入口速度为1 m/s时，φ的二次回归方程为：

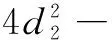
(12)

式中：8≤d2≤23.2；0.4≤k≤0.8。

采用约束优化算法得到最大压损比φ=4.227 0，对应的最优尺寸参数为d2=11.178 9、k=0.4。

当入口速度为3 m/s时，φ的二次回归方程为：

(13)

式中：8≤d2≤23.2;0.4≤k≤0.8。

采用约束优化算法得到最大压损比φ=5.423 2，对应的最优尺寸参数为d2=11.130 5、k=0.4。

对比入口速度1 m/s和3 m/s最优模型尺寸。考虑到数据计算误差，可以将2组最优模型尺寸视为一致。同时，该结果也说明了在模型尺寸最优的情况下，低速流场中任何速度的流体，在该模型下的压损比都可以达到一个最优值。经圆整，选取节流件大径11.15 mm，节流件小径与大径之比为0.4，节流件小径为4.45 mm，作为双向内外管差压流量计的最优模型。

3　流量计性能对比

为了研究双向内外管差压流量计在流量测量方面的特性，在同等工况下，选择最优尺寸模型，建立双向内外管差压流量计模型、内外管差压流量计模型(流体进入节流件方向不同的两种情况)进行模拟仿真，并对比3种模型的前后压损、节流件内外管压差和压损比等特性。

应用Fluent软件，分别建立3种流量计的模型。其中，入口边界条件设为速度入口。分别取0.5 m/s、1 m/s、1.5 m/s、2 m/s、3 m/s这5个速度等级，设置迭代步数1 000，步长为1。其他设置依照前文双向内外管模型优化时的方法，此处不作赘述。应用Fluent软件查看3种流量计模型在各个入口速度的压力云图时，三者在压差取压点附近的压力稳定。可以直观地看到：双向内外管差压流量计与内外管差压流量计(大管径流入)这2个仿真模型的内外压差明显，而另一个模型的内外压差对比并不明显。在后续处理中，计算出三者的压损比。为了更直观地对比压损比的变化，将计算结果绘制成折线图，不同速度下3组流量计的压损比折线图如图2所示。

图2　压损比折线图Fig.2　Line charts of pressure loss ratio

根据图2可以看出，在5级速度下，随着流速的不断增大，3组流量计的压损比都在增大。双向内外管差压流量计的压损比大于另外2组内外管差压流量计(不管流体从节流件哪个方向流入)，说明双向内外管差压流量计灵敏度更高，在测量过程中双向内外管差压流量计性能优于普通的内外管差压流量计。此外，从节流件小管径流入的内外管差压流量计的压损比最小。将压力损失同样绘制成折线图，不同速度下3组流量计的压力损失折线图如图3所示。

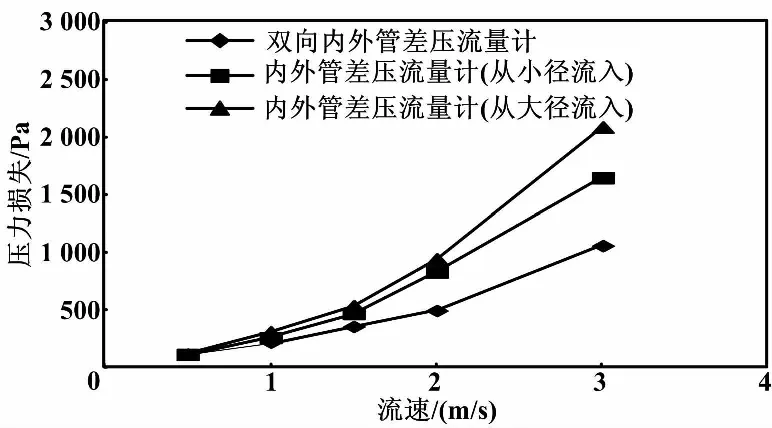
图3　压力损失折线图Fig.3　Line charts of pressure loss

在5级速度下，随着流速的不断增大，3组流量计的前后测点压力损失都在增大；但双向内外管差压流量计的前后测压点的压力损失小于另外2组内外管差压流量计(不管流体从节流件哪个方向流入)。由此可知，双向内外管差压流量计能够在测量过程中减少能量损失。该设计符合现代社会提倡的节能环保理念。在能耗方面，双向内外管流量计更加节能，表现出更多的测量优势。

4　结束语

由于内外管差压流量计在流体方向和取压位置的选择上存在争议，本文设计了双向内外管差压流量计。该流量计可实现盲插安装，且取压口的信号更加稳定。相对于通过数组结构模型数据进行对比选择出最优结构模型，本文将Fluent流体仿真软件与二次正交回归组合设计的试验方法相结合，能够准确地选择最优结构模型。以双向内外管差压流量计中节流件大径、节流件小径与大径之比为参数，正交组合出9组模型，利用Fluent对双向内外管差压流量计进行建模仿真，求得压损比。然后，正交回归分析得到回归方程，计算得到节流件大径为11.15 mm、节流件小径为4.45 mm、节流件小径与大径之比为0.4的最优模型，并通过仿真分析计算了最优模型的压损比。其压损比大于之前9组模型的压损比，验证了利用正交回归分析优化的可靠性。

将双向内外管差压流量计与普通内外管差压流量计进行对比分析。结果表明，前者的压损比大于后者，测量性能更加优越。双向内外管差压流量计的压力损失明显小于单向内外管差压流量计，流体动能损失更小，符合工业生产中的节能理念。在国家提倡节能减排的背景下，拥有节能环保和测量精准的双向内外管差压流量计，具有良好的工业实用价值，可以在化工与石油领域中进一步推广。

参考文献:

[1] 解海艇,黄富贵.流量仪表技术的发展趋势[J].自动化仪表,2013,34(4):69-72.

[2] 翟小金,沈新建,王光磊,等.新型差压式流量计性能研究[J].自动化仪表,2017,38(1):81-85.

[3] PENG L L,DONG H C,SHI Y,et al.Gas-liquid two-phase flow detection techniques based on internal and external tube differential pressure flowmeter[J].Applied Mechanics & Materials,2014(6):363-369.

[4] 许德福,王涛.浅谈差压式流量计的工作原理及选型[J].广东化工,2013,40(251):152-153.

[5] 周民,刘铁军,谢代梁.差压式双锥流量计研究及实验分析[J].自动化与仪表,2016,31(1):14-18.

[6] 方立德,张垚,王小杰,等.新型内外管差压流量计湿气测量模型研究[J].传感技术学报,2013,26(8):1173-1177.

[7] 李小亭,王小杰,方立德,等.新型内外管差压流量计特性研究[J].仪器仪表学报,2012,33(10):2371-2379.

[8] 范玉良,孟江,赵赞,等.内外管压差流量计的压力损失[J].机械设计与研究,2014,30(1):98-100.

[9] MENG J,LIU Z P,AN K,et al.Simulation and optimization of throttle flowmeter with inner-outer tube element [J].Measurement Science Review,2017,16(2):68-75.

[10]龙新平,王丰景,俞志君.喷射泵内部流动模拟与其扩散角优化[J].核动力工程,2011,32(1):52-57.