两电平逆变器长时域有限控制集模型预测控制
2018-04-17刘为杰洪兴福丁家宝
刘为杰,尹 疆,洪兴福,丁家宝
(中国空气动力研究与发展中心,四川 绵阳 621000)
0 引言
对于长时域有限控制集模型预测控制(long horizon finite control set model predictive control,LHFCS-MPC)而言,适当增加预测时域,可以获得更好的控制性能[1]。LHFCS-MPC的控制变量是离散的,因此属于组合优化问题。若采用穷举法来实现LHFCS-MPC,其计算量将随着预测时域的增加呈指数增长[2]。以两电平逆变器的LHFCS-MPC算法为例,当预测时域为N时,在每个采样周期内需要进行8N次代价函数的计算比较,计算量十分庞大,很难运用到高采样率系统中。
近年来,国内外有许多学者致力于减少LHFCS-MPC算法计算量的研究。Bemporad等在2002年提出了显式模型预测控制(explicit model predictive control,EMPC)。其主要思想是通过参数规划,将复杂的在线计算转化为离线计算,大大降低了在线计算时间[3]。随后,一些学者将EMPC技术成功运用到电力电子领域。Mariethoz S等人将MPC成功运用到脉宽调制(pulse width modulation,PWM)变流器和异步电机拖动系统中[4]。国内的张聚教授[5]系统地阐述了EMPC原理以及在电力电子领域中的多种运用实例。EMPC将大部分在线计算转化为离线计算,但随着预测时域的增加以及问题规模的扩大,状态空间分区也会急剧增加,对存储空间和在线查找时间提出了十分严峻的考验[6-7]。因此,EMPC更适用于小规模问题。另一部分学者则关注如何降低在线计算时间[8]。通过求解无约束二次线性规划问题,将长时域模型预测控制运用到电力电子领域。但这类方法需要增加脉宽调制器。文献[9]考虑变流器最优开关状态和次优开关状态,设计了一种预测步数为2的有限控制集模型预测控制(finite control set model predictive control,FCS-MPC)算法。但该方法很难推广到预测步数大于2的系统中。Tobias Geyer[10]提出了一种基于球形译码算法的LHFCS-MPC算法,但采用递归的方法执行效率较低,并且在初始时刻或动态时存在因球形译码算法初始半径偏大而计算量过大的问题。
本文将球形译码算法和回溯算法运用到LHFCS-MPC的滚动优化中,降低了算法的计算量。运用该算法,对两电平逆变器进行电流跟踪控制。在Matlab/Simulink平台上,搭建了两电平逆变器LHFCS-MPC控制系统仿真模型,对本文所提出算法的有效性进行仿真验证,并分析了控制系统的动静态性能。
1 两电平逆变器LHFCS-MPC
1.1 预测模型
两电平逆变器主电路拓扑结构如图1所示。图1中:Udc为直流电压;Sa、Sb和Sc为三个桥臂的开关状态(取值1或者0);L、R为等效负载,ia、ib、ic为交流侧电流。

图1 两电平逆变器拓扑结构图Fig.1 The topological structure of two-level inverter
为了便于计算,定义向量:
i=[iα,iβ]T
(1)
u=[Sa,Sb,Sc]T
(2)
则在αβ坐标系下,逆变器的数学模型可表示为:
(3)
式中:A、B为系数矩阵。
式中:P为Clarke变换矩阵。
将式(3)离散化,得:
i(k+1)=A1i(k)+B1u(k)
(4)
式中:A1=eATs,Ts为采样周期;B1=-A-1(I-A1)B,I为二阶单位矩阵。
式(4)即为逆变器的电流预测模型,用于预测下一时刻的电流值。
1.2 代价函数
当预测时域为N时,LHFCS-MPC的代价函数可以表示为[11]:
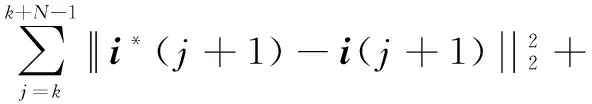
(5)
式中:λu>0,为权重系数。
式(5)中含有多个状态变量和输入变量。为了便于分析,定义向量:
(6)
则有:
I(k)=Ci(k)+DU(k)
(7)
式中:C、D为系数矩阵。
将式(6)和式(7)代入式(5),并整理得:
J=[U(k)+G-1R(k)]TG[U(k)+G-1R(k)]+c(k)
(8)
式中:
由此可以看出,c(k)与开关序列U(k)无关。而当系统参数确定后,矩阵G无需实时计算。当λu>0时,矩阵G为正定矩阵,则G-1也为正定矩阵。对G-1进行Cholesky分解,得:
G-1=LLT
(9)
则有:
G=L-TL-1
(10)
式中:L为下三角矩阵。
将式(10)代入式(8),且令H=L-1、Uunc=-LT×R(k),得:J=[HU(k)-Uunc(k)]T[HU(k)-Uunc(k)]+c(k)
(11)
在每个采样周期内,根据两电平LHFCS-MPC算法选择出开关序列U(k),使得代价函数J最小。而c(k)与U(k)无关,因此代价函数可以简化为:
J1=[HU(k)-Uunc(k)]T[HU(k)-Uunc(k)]
(12)
1.3 滚动优化
根据式(6)可知,U(k)共有3N个元素,每个元素取值1或者0。因此,U(k)总共有23N个可能取值。在此,不妨令U(k)的所有可能取值构成集合C。LHFCS-MPC算法在每个采样周期内,计算出使代价函数J1取值最小的的开关序列Uopt(k)。Uopt(k)即为最优开关序列。然后,将Uopt(k)的前3个元素,即uopt(k)作用于逆变器。这个过程即为滚动优化。
传统的LHFCS-MPC算法遍历集合C,将其中的每个元素均代入式(12)进行计算,经过比较后可得Uopt(k)。当预测时域N较大时,算法的计算量十分庞大。如当N=5时,需要计算32 768次代价函数。因此,当采样周期很小时,计算机无法在一个采样周期内完成一次完整计算。
以下将通过球形译码算法结合回溯算法,降低LHFCS-MPC算法的计算量。
1.3.1球形译码算法
球形译码算法的基本思想是:只搜索位于一个半径为r(k)的超球内的样本点[12]。参考球形译码算法的思路,设置初始半径为r(k),按照式(13)搜寻Uopt(k):
J1≤r(k)
(13)
因为式(12)中的H是下三角矩阵,因此,可以利用这一特性来减少计算量。将J1展开,得:[H(1,1)U(k)(1)-Uunc(k)(1)]2+[H(2,1)U(k)(1)+
H(2,2)U(k)(2)-Uunc(k)(2)]2+…+H(3N,3N)×
U(k)(3N)-Uunc(3N)(3N)2≤r(k)
(14)
在计算过程中,如式(14)左边部分的和大于r(k),则无需再往下进行计算。求和计算越往后,计算量越大。如果一旦发现不符合条件的开关序列就终止计算,将有效减少计算量。初始半径r(k)可以按照式(15)确定。
(15)
1.3.2回溯算法
LHFCS-MPC的滚动优化实际上属于组合优化问题。对于组合优化问题,使用回溯算法,可在一定程度上降低计算量。本文开关序列U(k)需要满足相电压和线电压跳变限制条件。为了便于计算,先不考虑开关跳变约束,选择子集树作为开关序列解空间树,如图2所示。

图2 开关序列解空间树Fig.2 The solution space tree of the switching sequence
回溯算法按照深度优先策略,搜索解空间树的节点。在搜索节点时,使用剪枝函数来避免无效的搜索。剪枝函数包括约束函数和限界函数。逆变器开关切换时,必须满足相电压和线电压跳变限制条件(即相电压和线电压每次变化不能超过一个电平)。因此,可以将电压跳变限制条件作为约束函数,如式(16)所示:
(16)
由式(14)可知,限界函数根据球形译码算法获得。值得注意的是,当回溯算法搜索到一个可行解时,更新球形译码半径,以逐渐逼近最优解。
回溯算法有递归和迭代两种实现方式。递归方式虽然代码简洁,但是执行效率不高;而迭代方式的特点与递归相反[13]。本文采用迭代式的回溯算法来实现球形译码算法,相应的伪代码如下:
while(k>=1)
if (k==1)d=0;
end
for (eachu∈{ 0, 1})
if(umeets the switching constraints)
U(k)=u;
d1= (Uunc(k)-H(k,1:k)*U(1:k))2+d;
Record(k)=d1;
if (d1<=r)
if(k==3N)r=d1;Uopt=U;
elsek=k+1;d=d1;
end
end
end
end
k=k-1;
if (k>=2)d=Record(k-1);
end
end
以上算法中,最耗时的步骤是计算H(k,1∶k)*U(1∶k)。得益于式(14),d1可以通过累加的形式进行计算,避免了重复计算。此外,程序还用数组Record记录每步d1的值。当算法回溯到上层节点时,无需再重新计算d1,进一步降低了计算量。
2 初始和动态时降低算法计算量
球形译码算法的关键是初始半径r(k)的选择。r(k)太小,会导致算法搜索不到解;r(k)太大,则扩大了搜索范围,将导致算法的计算量显著增加。按照式(15)计算r(k):在稳态时,r(k)的取值是较为合适的;但是在初始时刻或者参考电流突变时,r(k)的取值明显增大,算法的计算量也随之增加。在实际应用中,必须保证算法的计算量在每个采样周期内都维持在较低的水平。
针对上述问题,本文给出了相应的解决办法,具体描述如下。令m为稳态时初始半径最大值,在程序中进行判断。如果r(k)>kim(ki为一个裕量系数),按照预测时域N=1的情况来搜索最优开关序列;如果r(k)≤kim,则程序正常执行。这样既可在初始时刻和动态时,使得算法的计算量维持在较低的水平,又不会影响稳态时的控制性能。
3 仿真结果与分析
在Matlab/Simulink平台上,建立两电平逆变器LHFCS-MPC控制系统仿真模型,如图3所示。

图3 仿真模型Fig.3 Simulation model
对算法的计算量以及控制性能进行仿真分析。两电平逆变器参数如表1所示。

表1 两电平逆变器参数Tab.1 Parameters of the two-level inverter
3.1 算法的计算量
设仿真条件如下:预测时域N=5,λu=0.01,参考电流幅值为21 A,频率为50 Hz;当t=0.105 s时,令参考电流反向。记录每个采样周期内球形译码算法的初始半径r(k),如图4所示。从图4中可以看出,稳态时,初始半径的取值较小。
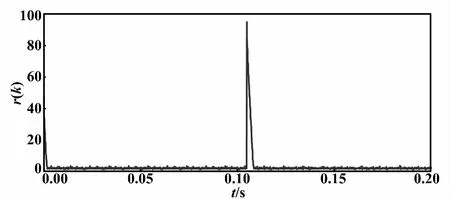
图4 算法初始半径变化曲线Fig.4 Initial radius variation curve of the algorithm
需要说明的是,本设计以算法在每个采样周期内搜索到的开关序列解空间树中的节点数量,来表征算法计算量。节点数量越大,则计算量越大。算法改进前后的计算量对比图如图5所示。

图5 算法的计算量对比图Fig.5 Comparison of the calculation amount
初始时刻以及动态时,初始半径突然增大。稳态时,算法的计算量较小,每个采样周期大概只需搜索700个节点;而初始时刻以及动态时,每个采样周期需要搜索上万节点,如图5(a)所示。采用本文方法,在初始时刻以及动态时,如果球形译码算法初始半径过大,则令预测时域N=1,并且以相应的算法搜索最优开关序列。稳态时,仍然使用N=5对应的算法。此时,每个采样周期内算法的计算量如图5(b)所示。可以看到,在整个仿真时段内,算法需要搜索的节点数限制在700以内,有效解决了初始时刻以及动态时算法计算量剧增的问题。
为了进一步分析两电平逆变器LHFCS-MPC算法的计算量的影响因素,针对不同的预测时域N,在不同的平均开关频率下(通过调节λu可以改变逆变器的开关率,一般情况下,λu增大,则开关频率减小),进行了仿真研究。统计每次仿真算法需要搜索节点数目的最大值,LHFCS-MPC算法计算量如表2所示。

表2 LHFCS-MPC算法计算量Tab.2 Calculation amount of LHFCS-MPC algorithm
3.2 控制性能
本节从动态性能和静态性能这两个方面,分析两电平逆变器LHFCS-MPC算法的控制性能。
①动态性能。

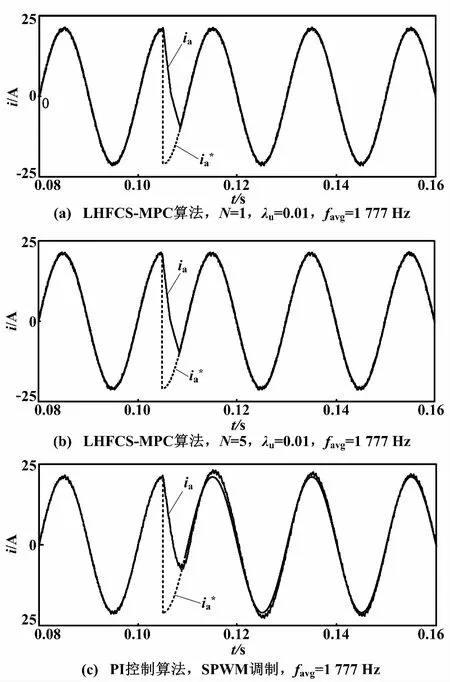
图6 动态电流波形Fig.6 Dynamic current waveforms
图6(a)为LHFCS-MPC算法在N=1时的电流波形。参考电流反向后,实际电流约在8 ms内重新准确跟踪到参考电流。图6(b)为LHFCS-MPC算法在N=5时的电流波形。与图6(a)对比发现,提高预测时域N不会影响电流的动态响应能力,因此本文方法不会对系统的动态性能产生影响。图6(c)为采用经典的比例积分(proportional integral,PI)控制及正弦脉宽调制(sinusoidal pulse width modulation,SPWM)调制得到的电流波形。载波频率(开关频率)设置为1 777 Hz,与LHFCS-MPC算法平均开关频率相同,采样规则为自然采样。从图6(c)中可以看出,电流突变后,实际电流大概经过两个电流周期(约40 ms)后,才能准确地跟踪到参考电流。由此可见,LHFCS-MPC算法的动态性能明显优于传统的PI控制。
②静态性能。
静态性能主要指的是稳态时逆变器输出电流谐波含量。电流谐波含量与开关频率紧密相关。一般而言,开关频率越高,则电流谐波含量越低。因此,在评价逆变器不同控制方法的优劣时,应当基于相同的开关频率。两电平逆变器6个开关器件的开关频率会略有差异,可定义逆变器平均开关频率favg:
(17)
式中:fa1为A相上桥臂功率开关的开关频率;fa2为A相下桥臂功率开关的开关频率。B、C相与之类似。电流谐波含量也取三相电流谐波含量的平均值。
对于LHFCS-MPC算法而言,调节λu可以改变开关频率;对于PI控制而言,调节载波频率,即可改变开关频率。记录每个开关频率和对应的电谐波含量,仿真结果如图7所示。图7中,每个离散的点代表一次仿真结果。利用Matlab cftool曲线拟合工具箱,以平滑样条拟合方式进行曲线拟合,得到两电平逆变器分别在LHFCS-MPC和PI控制策略下的电流谐波含量和平均开关频率的关系曲线。

图7 仿真结果Fig.7 Results of the simulation
从图7中可以看出,增大预测时域N,可以有效提高LHFCS-MPC算法的静态性能。其具体表现为:在相同的平均开关频率条件下,长预测时域对应的电流谐波含量更低。当N=1、400 LHFCS-MPC算法因计算量大而难以运用到逆变器等快速系统中。本文主要采用球形译码算法和回溯算法,对传统LHFCS-MPC算法进行了优化,降低了其计算量,使得该算法在快速系统中的应用成为可能。以两电平逆变器为研究对象,将LHFCS-MPC算法用于逆变器电流控制,并对算法的有效性和控制性能进行了仿真分析。仿真结果证明,该算法能够有效降低计算量。该算法在控制性能方面具有以下两个特点:①增大预测时域能够显著降低电流谐波含量,并且不会影响电流的动态响应速度;②两电平逆变器LHFCS-MPC算法的动态性能和静态性能均优于传统的PI控制。对于LHFCS-MPC算法存在的延时问题,后续工作将对其进行延时补偿,并对球形译码算法进行进一步优化。 参考文献: [1] GEYER T.A Comparison of control and modulation schemes for medium-voltage drives:emerging predictive control concepts versus PWM-based schemes[J].IEEE Transactions on Industry Applications,2011,47(3):1380-1389.[2] QUEVEDO D,GOODWIN G,DE D J.Finite constraint set receding horizon quadratic control[J].International Journal of Robust and Nonlinear Control,2010,14(4):355-377. [3] BEMPORAD A,MORARI M,DUA V,et al.The explicit linear quadratic regulator for constrained systems[J].Automatica,2002,38(1):3-20. [4] MARIETHOZS,DOMAHIDI A,MORARI M.High-bandwidth explicit model predictive control of electrical drives[J].IEEE Transactions on Industry Applications,2012,48(6):1980-1992. [5] 张聚.显式模型预测控制理论与应用[M].北京:电子工业出版社,2015. [6] BAYAT F,JOHANSEN T A,JALALI A A.Using hash tables to manage time-storage complexity in point location problem:Application to MPC[J].Automatica,2010,47(3):571-577. [7] GEYER T,TORRISI F D,MORARI M.Optimal complexity reduction of polyhedral piecewise affine systems[J].Automatica,2008,44(7):1728-1740. [8] 王东文,李崇坚,吴尧,等.永磁同步电机的模型预测电流控制器研究[J].电工技术学报,2014(s1):73-79. [9] 沈坤,章兢,王坚.一种多步预测的变流器有限控制集模型预测控制算法[J].中国电机工程学报,2012,32(33):37-44. [10]GEYER T,QUEVEDO D E.Multistep finite control set model predictive control for power electronics[J].IEEE Transactions on Power Electronics,2014,29(12):6836-6846. [11]陈虹.模型预测控制[M].北京:科学出版社,2013. [12]刘俊,魏急波,蓝兴.MIMO系统中球形译码算法的应用[J].现代电子技术,2008(5):49. [13]王晓东.计算机算法设计与分析[M].2版.北京:电子工业出版社,2004.4 结束语
