功能模块-抽象形态模型的构建方法与关键技术研究

□ 蒋 超 □ 余隋怀 □ 姚 澜

西北工业大学陕西省工业设计工程实验室 西安 710072

1　研究背景

在形态设计的信息化建模和表达方面，早期研究主要集中于产品的功能信息和形态信息两个方面［1-3］。近年来，根据工业设计学科的研究需要，设计师的形态设计意图信息也被讨论，并融入产品形态设计模型的构建过程中。通常而言，形态设计意图指设计师在产品设计过程中推荐和采用的形式主张和特性元素。目前，已有研究［4-5］利用动力学方程核函数来解析和表达产品的形态设计意图，但由于设计的操作性不甚理想，而并未得到广泛的应用。

为更好地解析产品的形态设计意图，且更完整地表达产品形态设计模型，笔者提出一种新的产品形态设计模型——产品功能模块-抽象形态模型（FSM）。FSM在产品功能和形态信息模型的基础上，通过定量计算产品概念模型中形态之间的相似度、重要度和中心度，明确形态间的关联性和重要性。其中，关联性可表征设计师的形式主张，重要性则可用于考察特征元素。

2　FSM概述

FSM是一种产品形态设计的表达形式，从工业设计角度出发，实现产品功能与形态间的求解路径，同时包含形态要素之间的关联信息。FSM更接近于工业设计师在进行真实设计活动时概念草图的设计形式，是一种更切实际的产品形态设计模型。在对产品的形态设计进行表达时，FSM使用抽象的几何形状概括产品的功能模块，并通过一定的约束和拓扑关系将这些具有抽象形态的功能模块组合起来。

为更好地展示FSM的特性，将抽象功能模型［6］、已有产品和FSM进行比较研究，结论见表1。所谓已有产品，指采用已经存在的产品作为产品的形态设计模型。

由表1比较可见，相比较于其它两种形态设计模型，FSM采用抽象形态单元描述功能模块，通过对功能单元进行组合，并对形态之间存在的关联性和重要性进行补充分析，可以将设计师隐喻在形态之间的设计意图发掘出来，具有更高的信息完整性和设计可塑性。

3　FSM构建关键技术

3.1　基于几何相似度的形态关联性计算

几何相似度的形态关联性指标，可由形态的相似程度表征。两条曲线段的几何相似度大于判断值，则可以认为这两条曲线相关。对两条曲线段插入评估节点，节点矢量P均设置为规范参数域［0，1］。在此规范参数域中，在节点矢量上按均匀参数取点的方法，取出两个评估点序列，可以概括两条曲线的基本特征，即两个评估点序列中的点可以分别代表两条曲线，且两个评估点序列含有相同个数的点。

假设 CS和 CL分别是在曲线 S［CS（0），CS（1）］和 L［CL（0），CL（1）］上取出的在世界坐标系下包含 k+1 个评估点的坐标序列，即：

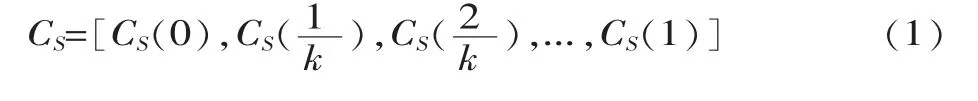
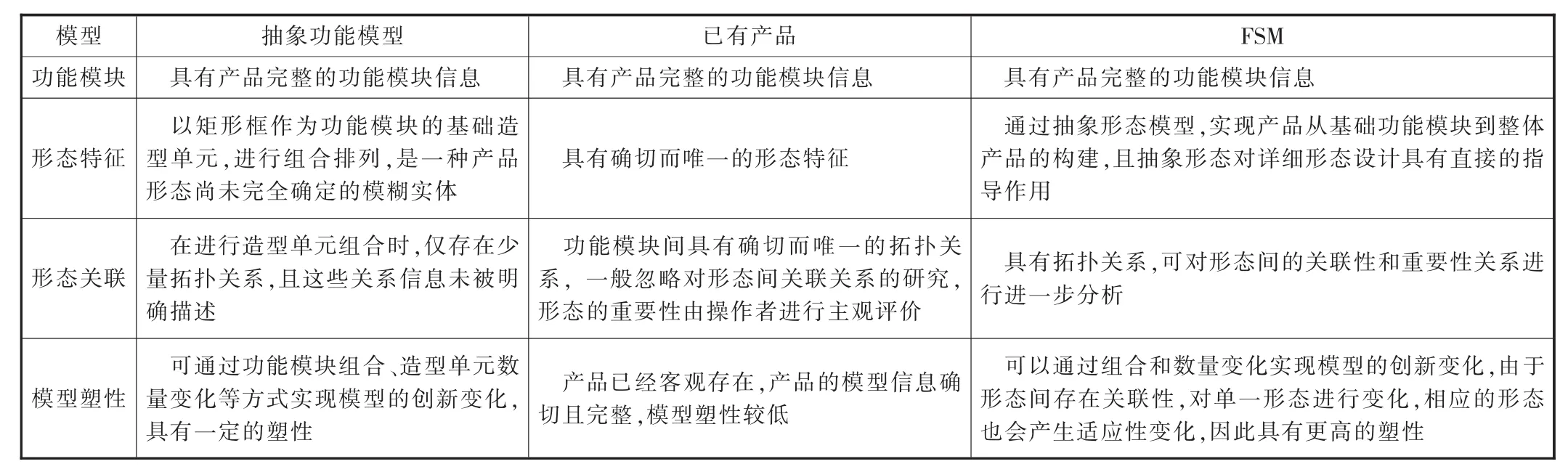
表1　形态设计模型比较研究结论

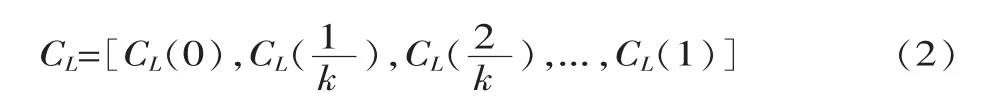
OS和 OL分别是曲线 S［CS（0），CS（1）］和 L［CL（0），CL（1）］的质心，即：

式中：ωi为CS和CL两序列中第i点对应的权值，0≤

以曲线 S［CS（0），CS（1）］和 L［CL（0），CL（1）］各自质心为原点的笛卡尔直角坐标系可称为质心坐标系，则CSS和CLL分别是CS和CL各自质心坐标系下的坐标序列。

曲线 S［CS（0），CS（1）］和 L［CL（0），CL（1）］的最小均方根偏差lmr为：

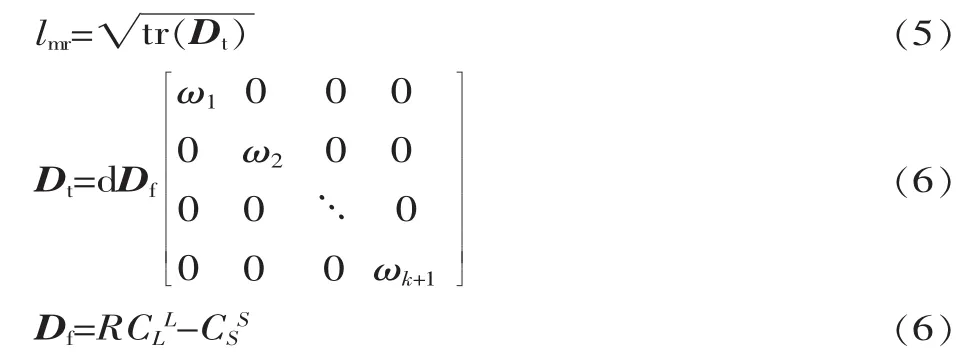
式中：tr（Dt）为 Dt的迹；Dt为加权误差矩阵；R 为经卡巴斯基算法［7］得出的两条曲线重叠时CLL所产生的旋转角；Df为CLL经卡巴斯基算法旋转平移后与CSS的误差矩阵。

最小均方根偏差lmr包含了CS和CL两个序列中的所有点，因此可以将lmr作为两曲线的相似性指标。两曲线的相似性定义为：给定一个相似度ε，ε＞0，对于曲线 S［CS（0），CS（1）］和 L［CL（0），CL（1）］，当曲线 L［CL（0），CL（1）］通过旋转和平移变换为 L″［CL″（0），CL″（1）］后，S［CS（0），CS（1）］与 L″［CL″（0），CL″（1）］之间的最小均方根偏差 lmr＜ε，则称在相似度 ε 下曲线 S［CS（0），CS（1）］和 L［CL（0），CL（1）］相似。

通过对曲线间lmr的计算，可得到曲线间的相似度值，即关联性值，并构建相关性网络。网络的节点表示形态，节点间的连线表示关联性。可在连线上标注关联性值lmrab，a和b表示两个不同形态。为了使相关性网络的结构更清晰，可在全系统内设定相似度ε，去除关联性较低的连线，来简化网络结构。与某曲线关联性大于ε的曲线数量为u，则该曲线的中心度值G=u。相关性网络一般结构如图1所示。

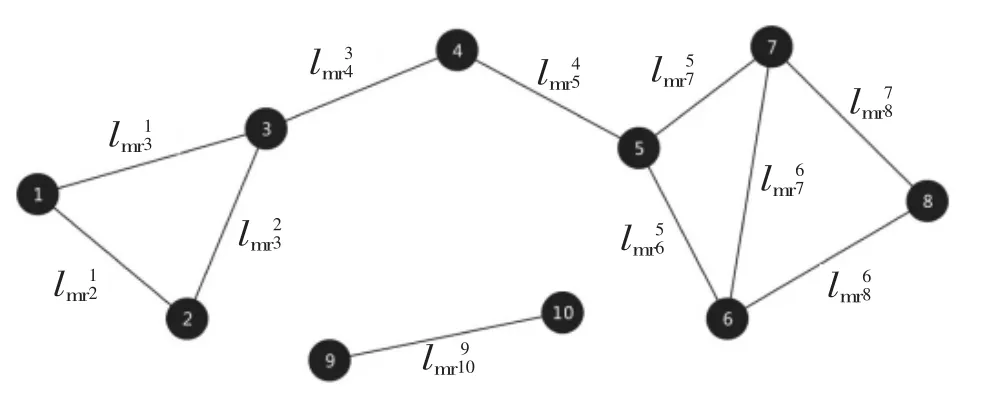
▲图1 相关性网络一般结构

3.2　基于效率矩阵的节点重要度计算

在通过上述方法建立的相关性网络中，形态的重要性可用节点重要度表示。基于重要度贡献矩阵的评价，认为相关性网络中节点之间存在依赖关系，即形态的几何相似性。因此，针对相关性网络，提出一种改进的基于效率矩阵的节点重要度评估算法。这一方法不仅可以考量节点重要度值，而且可以考量全网络节点间的重要度贡献，即用节点重要度值来表示节点的局部重要度，用节点的重要度贡献来表示节点的全局重要度。可见，相关性网络中的各节点对其它节点的依赖程度可以通过效率矩阵来计算［8］。

假设某相关性网络G=｛V，M｝，具有n个形态节点和 m 条边，V=｛V1，V2，...，Vn｝， 为网络中的形态节点，M=｛M1，M2，...，Mm｝，为形态节点之间的关联边。 eij为节点Vi和Vj间的效率值，则相关性网络的效率矩阵E为：

相关性网络中某节点对其余节点的依赖度矩阵H为：

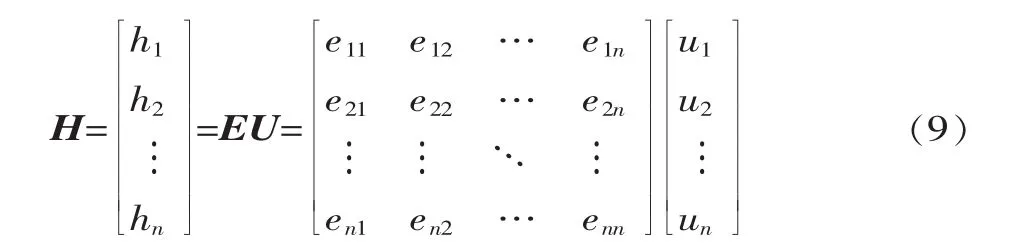
式中：h1，h2…hn为相关性网络中各节点的重要度值；U为相关性网络的节点中心度矩阵；u1，u2…un为相关性网络中各节点的中心度值。

第i个节点Vi在相关性网络中的相对重要度hi为：

式中：hij为节点 Vj对节点 Vi的重要度贡献，hij=eijuj，uj为第j个节点Vj的中心度值。

相关性网络节点Vj对节点Vi的重要度贡献不仅和节点间的效率值eij大小有关，而且和节点Vj的中心度值uj大小有关。如果节点Vj越大，uj越大，则节点Vj对节点Vi的重要度贡献就越大。在考虑网络节点对待评估节点重要度贡献的基础上，结合待评估节点自身的局部重要度，得到第i个节点Vi的重要度di为：

可见，经过归一化处理后，第i个节点Vi的重要度 di′为：

将重要度计算结果输入相关性网络，可得到形态基因关系图。这种形态基因关系图包含有节点关联性值和节点重要度两方面信息，节点的大小表示节点的重要度，如图2所示。

4　FSM构建方法

FSM的构建方法为：从产品功能层面出发，通过对零件级的末级功能模块赋予抽象形态，并分析形态间的关系，从而实现产品功能-形态-意图的求解。FSM构建流程如图3所示，由图3可以看出，一般的功能模块设计模型仅求解到形态，但FSM求解更为深入，是一种更为全面的形态设计模型。

FSM的主要构建步骤如下。

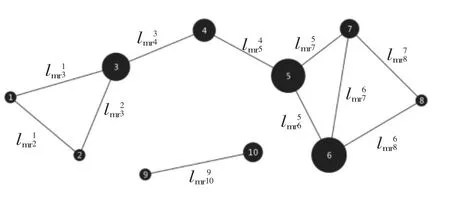
▲图2 形态基因关系图

（1）产品功能模块设计。对产品功能进行分析，并对产品功能模块之间的关系进行研究，通过子功能实现产品的总体功能。构建功能技术矩阵，最终将顶层功能分解为若干个末级功能。

（2）依照产品功能需求，通过指定功能模块的线条围合数量和相应参数建立抽象功能形态，并对构成产品末级功能的零件赋予抽象形态。

（3）指定抽象形态间的拓扑关系，将抽象形态进行组合，完成几何模型的初步构建。

（4）采用关联性计算公式计算形态之间的关联性，设定相似度条件参数，并构建形态的相关性网络。

（5）采用效率矩阵对相关性网络进行分析，并计算各个节点的重要度。

（6）最终明确FSM中各形态之间存在的关联性和重要性关系。

5　实例验证

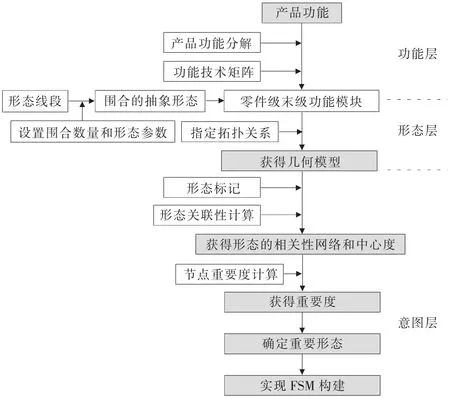
▲图3 FSM构建流程图

为更好地对FSM构建关键技术进行阐述，以实际项目中编号为Sa5的某款台灯遥控器形态设计为例，对形态之间的关联性和重要度进行分析和计算。对Sa5进行形态标记，如图4所示，图4中短斜线为线段分割线，a22和a31重合。

5.1　关联性计算

对形态的关联性进行计算，每次将两条形态基因的取值代入式（1）、式（2），应用式（3）、式（4）求出各自的质心，并应用式（5）～式（7）求出两两形态之间的lmr。

为方便计算，在直角坐标系中设定a11的总长为 2，并将质心定为点（0，0），关联性计算点的取值见表2。归一化后的关联性最终计算结果见表3。

在a11和a21形态线段上各取20个点，若取点数量不同，计算结果会有轻微差异。

5.2　重要度计算

采用表3结论，将形态基因视为一个复杂网络。以中心度为节点的重要度贡献赋值，以关联性为节点效率赋值。应用式（8）、式（12）对节点的重要度进行计算，归一化后的重要度结果见表4。

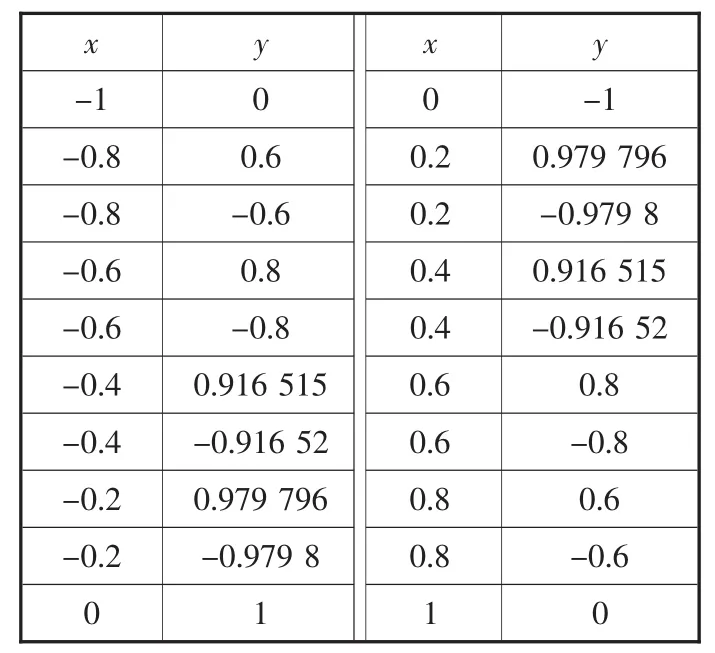
表2　a11关联性计算点取值

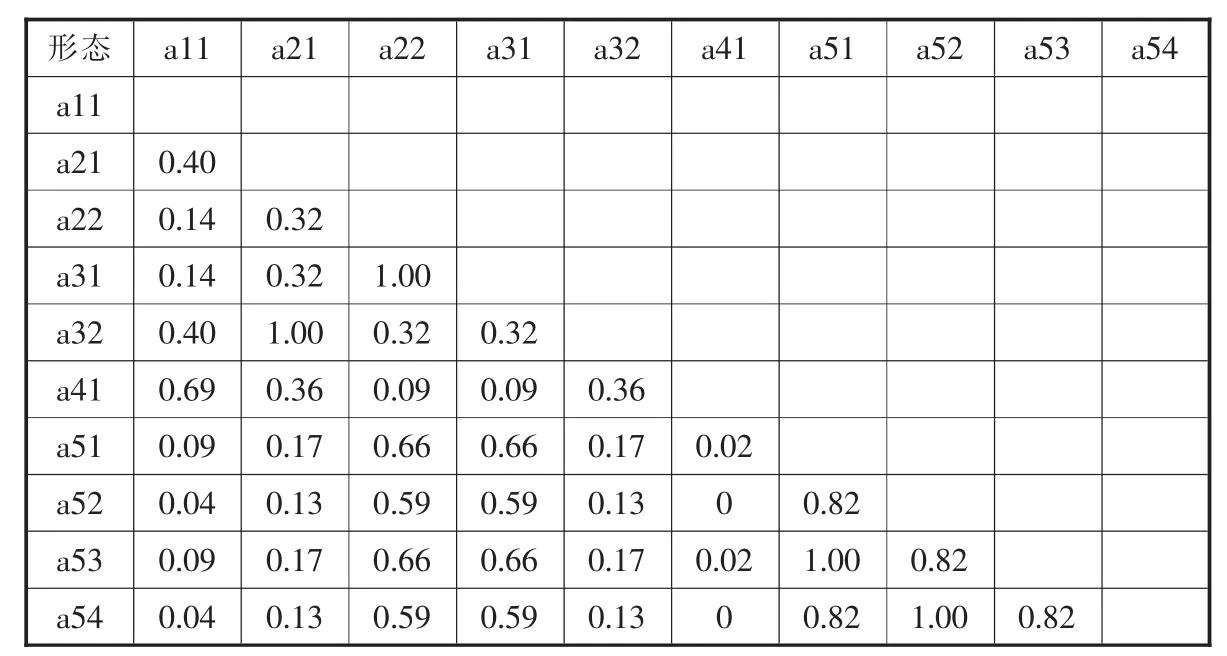
表3　归一化后关联性计算结果

表4　归一化后重要度计算结果

根据上述数据构建形态基因关系图。设相 似 度 ε 为0.4，当关联性计算结果大于0.4时，将两形态节点进行连线。方案Sa5的形态基因关系图如图5所示。

综上所述，方案Sa5的FSM既包含了完整的功能信息和基础的抽象形态信息，又具有明确的形态间关联性和重要度信息，因此可以说，方案Sa5的形态设计模型信息较为完整。

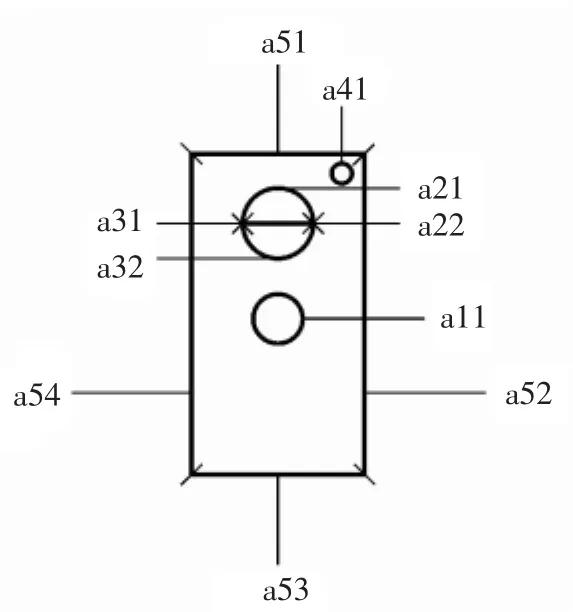
▲图4 Sa5形态标记

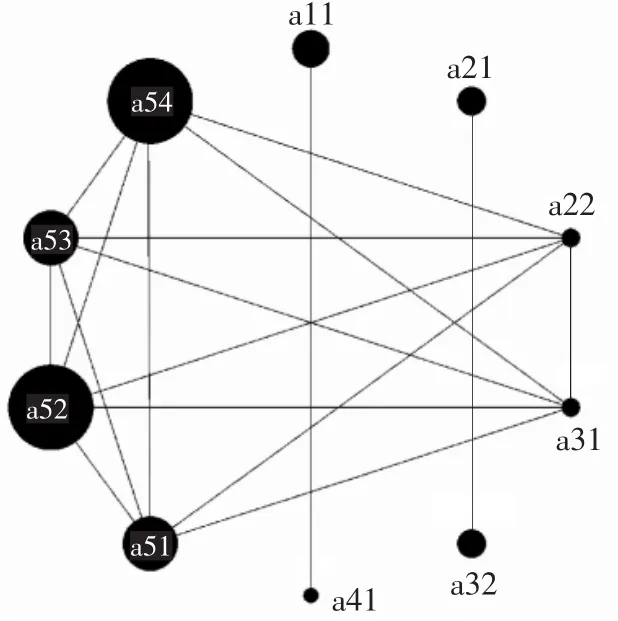
▲图5 Sa5形态基因关系图

6　结论

产品的形态设计模型是产品形态设计的初期结果，也是后期进行详细设计的基础。笔者提出的FSM在包含产品功能和几何信息的同时，进一步分析产品形态之间的关联性和重要性。通过对形态之间关系的进一步挖掘，一方面在一定程度上解析了设计师初始的形态设计意图，可以使设计更深入和有的放矢；另一方面明确了形态之间的关联性，可以避免在深入设计时对个别形态进行孤立操作，忽略产品形态之间的协同作用。可见，FSM是一种更为完整和合理的产品形态设计模型。

［1］ 潘云鹤，耿卫东，童欣.面向智能CAD的分层构造自动型方法［J］.软件学报.1996，7（5）：280-285.

［2］ CHAKRABARTI A，BLIGH T P.A Scheme for Functional Reasoning in Conceptual Design ［J］.Design Studies，2001，22（6）：493-517.

［3］ TAY F E H，GU J X.Product Modeling for Conceptual Design Support［J］.Computers in Industry，2002， 48（2）：143-155.

［4］ PERRY M A，ATHERTON M A，BATES R A，et al.Bond Graph Based Sensitivity and Uncertainty Analysis Modelling for Micro-scale Multiphysics Robust Engineering Design［J］.Journal of the Franklin Institute， 2008，345（3）：282-292.

［5］ BANERJEE N，SAHA A K， KARMAKAR R， et al.Bond Graph Modeling of a Railway Truck on Curved Track ［J］.Simulation Modelling Practice and Theory，2009，17 （1）：22-34.

［6］ 简召全.工业设计方法学：修订版［M］.北京：北京理工大学出版社，2000.

［7］ 臧永灿，徐建明，朱自立，等.非均匀有理B样条曲线优化匹配组合［J］.中国图象图形学报，2016，21（3）：331-338.

［8］ 范文礼，刘志刚.一种基于效率矩阵的网络节点重要度评价算法［J］.计算物理，2013，30（5）：714-719.

［9］ 罗阿妮，张桐鸣，刘贺平，等.机械行业三维建模技术综述［J］.机械制造，2010，48（10）：1-4.

［10］李强，方水良.基于参数化的产品变形设计建模研究与实现［J］.机械制造，2006，44（1）：11-14.