仿人机器人的步态规划研究

□ 王宪伦 □ 冯现东 □ 姜鹏鹏

青岛科技大学机电工程学院 山东青岛 266061

1　研究背景

传统履带式或轮式机器人由于受本体结构限制，适宜在较为平整的地面上工作。仿人机器人具有灵活的双腿设计，因此具备人类行走的步态特性，对于不平整地面具有较大的灵活性和良好的适应能力。如果仿人机器人不能精确模拟人类行走的步态特性，那么其优势也将荡然无存。为实现仿人机器人的行走稳定性，除了完善控制系统算法，增加必要的传感器之外，机器人精确的步态规划也是解决问题的关键技术［1］。

根据行走步态，仿人机器人的步态分为静态步行和动态步行［2］。相比速度较慢的静态步行，动态步行速度较快，但容易出现稳定性问题，即仿人机器人容易发生左右或前后倾覆。为了提高仿人机器人的行走稳定性，提出用于反映动态步行稳定性的零力矩点概念。零力矩点法是目前步态规划方法中影响范围最大、应用最广泛的方法，由零力矩点法得到的动态步行能长期保持令人满意的效果。笔者基于零力矩点法对仿人机器人的步态规划进行研究，具有一定的实用价值。

2　仿人机器人本体结构设计

笔者所设计的仿人机器人，其颈部关节配置两个自由度，肩部配置两个自由度，肘部配置一个自由度，腰部髋关节配置三个自由度，膝关节配置一个自由度，踝关节配置两个自由度。可见，器人整体共配置20个自由度，基本能够完成预定动作，实现仿人行走和舞蹈等。仿人机器人本体结构如图1所示。

3　步态规划

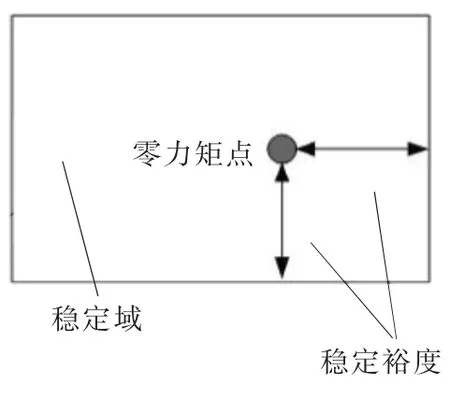
▲图2 稳定裕度示意图

首先对机器人进行步态规划，然后根据零力矩点公式求出零力矩点曲线，据此分析设计的步态稳定性，并选取相对稳定裕度最大的步态规划作为仿人机器人的最优步态规划。如图2所示，通过选取合适的结构参数和运动参数，使零力矩点轨迹始终落在单双脚支撑范围内，实现机器人的稳定行走，这是对仿人机器人进行步态规划的主要目的［3］。通常，将零力矩点到支撑凸多边形边界的最短距离作为机器人步行系统的稳定裕度，稳定裕度可以体现行走时稳定性的好坏。稳定裕度值越大，则机器人行走就越稳定。

3.1　零力矩点坐标建立与计算

通过重力和惯性力合力的零力矩点来定义坐标公式，并利用达朗贝尔原理［4］进行推导。由于机器人的运动过程为单双腿支撑的交换，因此为了正确描述每条腿所受到的地面反力特点，设参考坐标系的原点坐标为单脚支撑时支撑脚的中心，且支撑面与参考坐标系的XOY平面重合。

根据机器人模型参数的定义，由达朗贝尔原理可知，除地面对机器人脚底的反作用力和反作用力矩之外，可以将机器人行走时受到的全部作用力和力矩向参考坐标系的原点作化简处理，获得沿X、Y、Z轴三个方向的分力及绕X、Y、Z轴的力矩。

式中：Fx、Fy、Fz依次为沿 X、Y、Z 轴方向的分力；依次为第i个简化杆沿X、Y、Z轴方向的质心加速度分量；mi为第i个简化杆的质量；g为重力加速度。

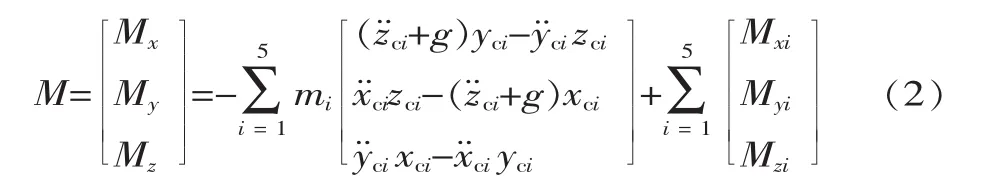
式中： Mx、My、Mz依次为绕 X、Y、Z 轴的力矩；xci、yci、zci为第i个简化杆的质心位置坐标。

根据式（1）与式（2），将作用于机器人上的合力从参考坐标系原点移至XOY平面上的零力矩点P（xzmp，yzmp，0），使机器人绕X轴和Y轴的倾覆力矩为0，即：

将式（2）中的 Mx、My代入式（3），得：

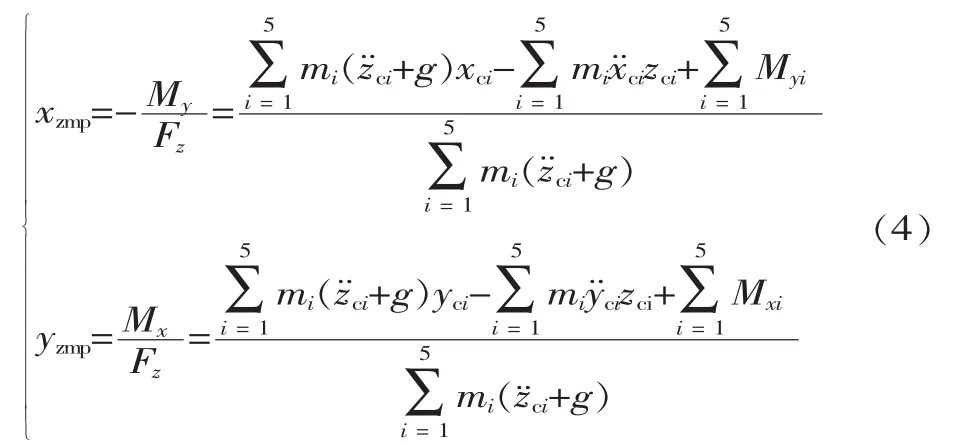
静态步行时，忽略机器人所受的惯性力，则式（4）变为：

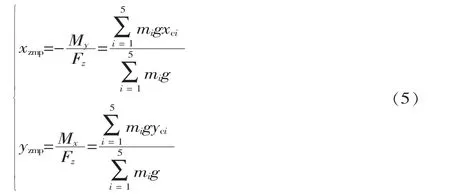
除机器人所受的地面反作用力矩外，其余所有力矩均转化为作用在零力矩点P（xzmp，yzmp，0）的一个力矩：

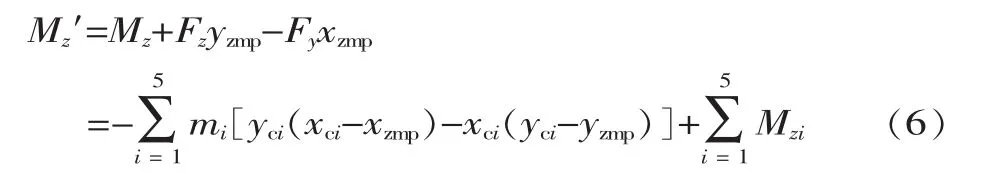
3.2　步态规划思路

步态规划的基本思路如下：根据仿人机器人行走时对步态动作特点的要求，确定步距、步行周期、步长等参数；根据各关节的约束条件，对机器人双腿的髋关节及踝关节进行合理运动规划，利用三次样条函数［5］生成髋关节和踝关节的运动轨迹方程，以便使轨迹曲线在连接处均匀光滑过渡；基于机器人各个关节的几何角度关系，通过MATLAB软件程序，求出膝关节及其它关节的运动轨迹，并生成轨迹曲线［6］；利用零力矩点公式计算出机器人的质心轨迹，通过在可变范围内寻找最优解，确认稳定裕度最大的组合参数，并将通过这些参数计算出的步态规划数据作为最终的规划结果。

三点式规划法主要针对踝关节的关键点进行运动规划，即将起步、摆动脚支撑面最高点和落地这三个点作为运动关键点进行运动规划。通过三次样条插值对机器人的运动关键点进行插值，以及对起步与落地时刻各关节的速度及加速度施以约束，得到能够保证机器人稳定行走的光滑运动曲线。三点式规划法如图3所示。

3.3　平面步行步态规划

仿人机器人完整的行走过程包括起步准备阶段、加速阶段、周期性运动阶段、减速阶段和停步恢复阶段这五个时间段，其中周期性运动阶段又包括左脚步行周期和右脚步行周期。由于周期性运动阶段是仿人机器人行走的主要过程，因此笔者的研究主要针对机器人进行周期性运动规划。

与人类相似，仿人机器人的步行周期包括单脚支撑期TD和双脚支撑期TS，则步行周期T=TS+TD。设置步态运动规划参数，抬脚高度设为H，步长设为L，第k步的起始时间为（k-1）T。步长L按实际需求设定，约为一个步长即可。

假设机器人向前周期运动中先摆动左脚，即先迈左脚再迈右脚，则XOZ平面的坐标原点设在支撑脚的中心，那么第k个周期摆动脚踝关节质心的起始坐标为（（k-1）L，0），最高点位置为（（k-1）L+L/2，H），落地时的坐标为（kL，0），由以上三个关键点可以得到以下约束方程组：

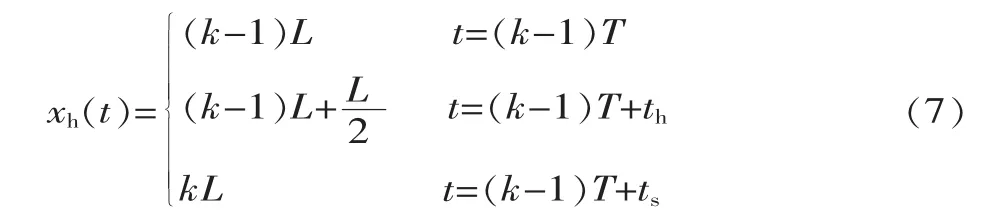
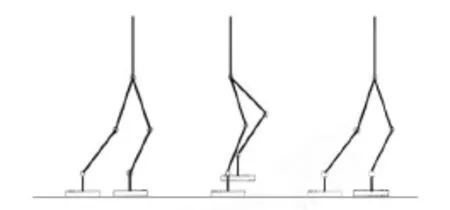
▲图3 三点式规划法示意图

式中：ts为走一个步长所需的时间；th为走半个步长所需的时间。

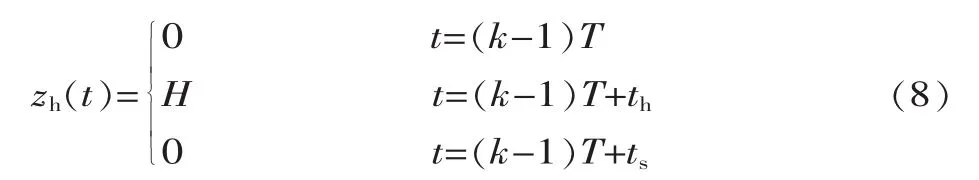
由行走过程可知，摆动脚在kT时刻初始速度为0，同时为了使脚部与地面在落脚时刻的冲击最小，摆动脚在落地瞬间速度亦需要降为0，因此需将摆动脚在 kT 和 kT+Ts时刻 xh（t）和 zh（t）的导数均设置为 0，即速度均为0，可以得到以下约束方程组：

利用三次样条插值函数对上述关节轨迹进行插值规划，即可得到光滑、连续的轨迹曲线。

对机器人前向运动中髋关节X轴方向和Z轴方向分别进行轨迹规划。对X轴方向进行规划时，因X轴方向保持匀速运动，在X轴方向的运动选取三个关键点即可，分别为初始抬脚位置、偏转最大位移处和落脚复位处。髋关节在X轴方向的约束方程组为：

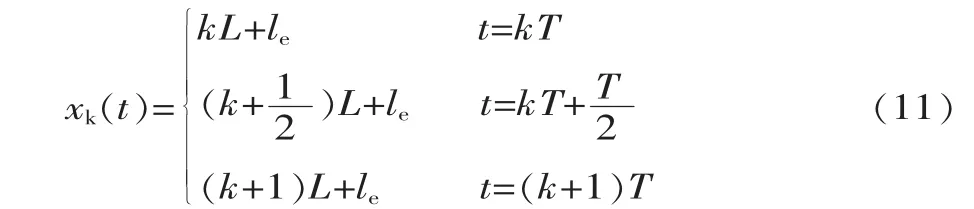
式中：le为初始抬脚时刻沿X轴正方向髋关节的坐标到坐标原点的距离。

由于机器人自身结构及运动特点，在周期行走过程中两腿摆动，上身基本保持不变，因此对髋关节在Z方向的轨迹进行规划时，设定机器人的髋关节保持在某一固定高度，即将髋关节在Z轴方向的坐标设为一个常值Hk，Hk的值由实际行走情况确定。

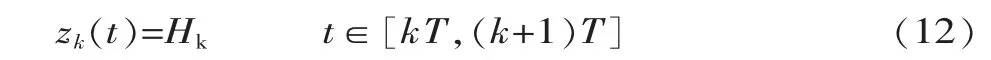
对于Hk的取值范围，如图4所示，由给定的步长L及三角形三边大小关系可以求得：

至此，仿人机器人在前向运动中髋关节和踝关节的轨迹规划已经完成，接下来对机器人在侧向平面运动的步态进行规划。

机器人在侧向平面内运动时只需对一个变量参数进行规划，即侧向转角αce。侧向平面内机器人的运动应满足以下约束方程：

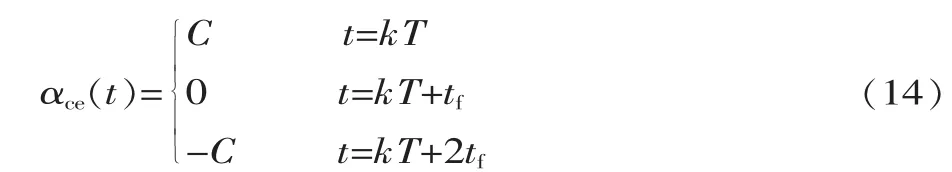
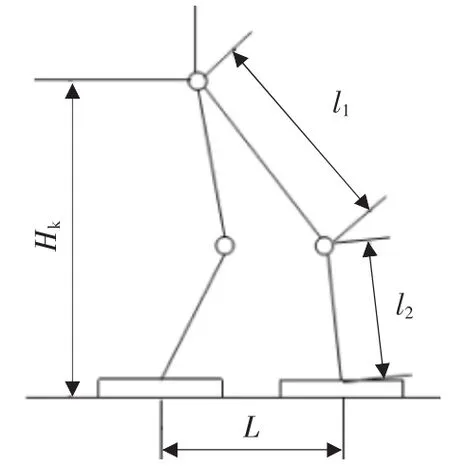
▲图4 髋关节高度示意图

式中：C≤|arctan（a/b）|，a 为机器人质心到支撑脚中心的水平距离，b为机器人质心至地面的垂直高度；tf为机器人上躯体从一侧摆到中间位置时所需的时间。

按照上述约束条件，利用三次样条函数插值即可生成侧向转角αce与时间t的曲线，计算出αce与t的关系式。

4　步态仿真

行走过程规划结束后，应用MATLAB软件编写计算程序，求解所需参数值，并在MATLAB中进行仿真求解。设机器人双腿的小腿长L1=L5=75 mm，大腿长L2=L4=80 mm，取步长 L=100 mm，步行周期 T=1 s，抬脚高度H=15 mm，髋关节质心高度Hk=135 mm，行走时侧向转角αce=5°，在MATLAB中机器人平面前向步态行走时各关节转角曲线的仿真结果如图5所示。

由图5可见，完成规划动作所需的各个关节转角值是连续变化的，没有产生突变，即机器人关节转动是连续的，其后可利用虚拟样机的仿真来验证计算所得的关节转角是否合理。

5　虚拟样机仿真

将SolidWorks软件绘制的机器人三维样机模型（图6）导入ADAMS软件，为了模拟实际运行环境，需要设置重力方向和大小。在机器人双脚与地面之间添加接触和摩擦力，将通过MATLAB编程得到的各关节运动曲线文本数据以样条曲线形式导入ADAMS，添加至关节驱动约束函数，这样即可在ADAMS中进行仿真［7］。仿真运行成功后，通过后处理分析，检验步态规划是否合理，并根据实际环境对ADAMS仿真环境进行调整。虚拟样机［10-11］行走动画如图7所示。

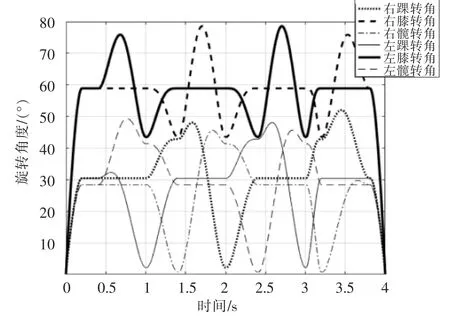
▲图5 机器人平面前向步态关节转角曲线

▲图6 SolidWorks机器人三维样机模型

▲图7 虚拟样机行走动画

6　结束语

笔者介绍了零力矩点法的稳定性判据，推导了零力矩点法的坐标计算公式。从行走稳定方面考虑，采用基于三次样条函数的三点式规划法对动态步行进行规划，保证了机器人的步行质量。通过虚拟样机仿真结果后处理，得到躯体质心在X、Y、Z轴方向的位置变化曲线。躯体质心在X、Y轴方向的仿真运动轨迹与规划的质心轨迹吻合较好，在Z轴方向的运动轨迹有周期性小幅波动，波动幅度在3 mm之内，对机器人行走稳定性的影响较小。

［1］ 张伟，杜继宏.双足步行机器人的步态规划［J］.计算机工程与应用，2002（13）：214-216.

［2］ CHEN X Y， LI Z X.Walking Pattern Design and Feedback Control for Humanoid Robot［C］.Intelligent Control and Automation，2008.WCICA 2008.7th World Congress on，Chongqing，2008.

［3］ 谭民，徐德，侯增广.先进机器人控制［M］.北京：高等教育出版社，2007.

［4］ 哈尔滨工业大学理论力学教研室.理论力学［M］.7版.北京：高等教育出版社，2009.

［5］ 封建湖，车刚明，聂玉峰.数值分析原理［M］.北京：科学出版社，2012.

［6］ SREENATH K，PARK H W，POULAKAKIS I，et al.A Compliant Hybrid Zero Dynamics Controller for Stable，Efficient and Fast Bipedal Walking on MABEL ［J］.The International Journal of Robotics Research， 2011， 30 （9）:1170-1193.

［7］ 李增刚.ADAMS入门详解与实例［M］.2版.北京：国防工业出版社，2014.

［8］ 朱秋国.仿人机器人结构设计与分析［D］.杭州：浙江大学，2011.

［9］ 魏航信.仿人跑步机器人快速跑步研究［D］.西安:西安电子科技大学，2006.

［10］王国强，张进平，马若丁.虚拟样机技术及其在ADAMS上的实践［M］.西安：西北工业大学出版社，2002.

［11］杨萍，樊迪.小型双足机器人步态规划研究［J］.机械制造，2015，53（9）：39-42.