基于Bagging集成聚类的改进遗传算法在装配线平衡中的应用*
2018-04-16李爱平赵亚西
□ 李爱平 □ 赵亚西
同济大学机械与能源工程学院 上海 201804
1 研究背景
在企业实际生产中,改善装配线的生产效益是研究重点。装配是制造与信息控制相结合的过程,设计出优良的装配线平衡方案,能够使装配线高效且可靠地运行,进而提高生产效率,增加企业效益,可见,研究装配线平衡具有很大的实际意义。装配线平衡问题按不同的优化目标主要分为三类[1-2]:① 生产节拍一定,求最优工作站数;② 工作站数固定,求最优生产节拍;③工作站数已知,求最优平滑因子。装配线平衡问题是典型的非确定多项式难题,对于求解算法有较高的要求,近年来主要以遗传算法等启发式算法为主,由于算法可行解过多,为了搜索出更优的可行解,算法需要改进。
张子凯等[3]针对大规模混流U型装配线平衡问题,提出了一种基于多级随机分配编码的改进遗传算法,算法在降低计算复杂度的同时能准确求出问题较优解。梁雨生等[4]针对装配线平衡问题,提出了一种基于可行作业序列的多种群遗传算法,扩大了搜索的空间范围,有效避免产生局部最优的情况。扈静等[5]针对传统混合装配生产线缺乏一工位多产品研究的现状,设计了基于激素调节机制的改进遗传算法适应度函数,以及选择、交叉与变异算子,对一工位多产品的混合装配生产线平衡问题模型进行求解,提升了算法性能。董双飞[6]结合遗传算法与混流装配线的特点,对遗传算法中初始种群的产生、算法的可视化操作、交叉与变异操作的方式及概率的设置进行改进,并提出种群扩张机制,提高了算法的全局搜索能力。李险峰[7]针对传统遗传算法在种群数目有限的情况下呈现早熟问题进行分析,提出并实现了一种加入改进遗传算子策略,且结合模拟退火思路的混合遗传算法。韩煜东、董双飞等[8]设计了基于自然数序列和拓扑排序的改进遗传算法,对模型进行求解时通过改进交叉、变异操作来保护优秀基因,同时提出了种群扩张机制,在求解效率和求解质量方面取得显著成效。刘雪梅等[9]基于工位复杂性测度提出了一种随机型装配线平衡优化方法,并将基于动态步长法的改进遗传算法用于优化求解。陈星宇[10]提出一种双种群遗传算法,设计了基于优先关联矩阵的编码、译码,以及适应度设计、交叉选择和变异算子,在求解装配线平衡问题时有显著成效。Hou Liang等[11]针对产品族装配线提出了一种改进的双种群遗传算法,同时为了弥补传统解码方法的不足,提出了一种新的解码算法,加快了算法的搜索速度。
综上所述,学者们从编码、解码、交叉、变异、选择等各环节对遗传算法做出改进,但是尚未从近亲不能繁衍后代的生物学角度考虑算法的改进方式。笔者为了提高遗传算法的搜索深度,考虑生物学角度近亲不能交叉的规则,建立一种Bagging集成聚类方法用于分析种群个体间的亲缘关系,并基于此方法改进遗传算法的交叉环节,在双目标装配线平衡优化问题中提高算法的搜索深度,得到更优的可行解。
2 基于Bagging集成聚类的种群聚类分析
传统遗传算法在求解装配线平衡等非确定多项式难题时,常常表现出搜索深度不足的问题,为了提高遗传算法的搜索深度,笔者提出一种Bagging集成聚类算法,用Bagging对几个K均值算法基学习器进行集成学习,经过投票机制后得出每个种群个体所属的类别。
2.1 K均值聚类算法
K均值算法的原理是使聚类的所有样本到聚类中心距离的平方和最小,是经典的硬聚类算法。
K均值聚类算法使用的聚类准则函数是误差平方和准则:

为了优化聚类结果,应使准则最小化。
第一步,给出n个混合样本,令I=1,表示迭代次数,选取 K 个初始聚合中心 Zj(I),j=1,2,...,K。
第二步,计算每个样本与聚合中心的距离D(xk,Zj(I)),k=1,2,...,n,j=1,2,...,K。 若 D(xk,Zj(I))=min{D(xk,Zj(I)),k=1,2,...,n},则 xk∈wi。
第三步,计算 K 个新聚合中心,Zj(I+1)=,j=1,2,...,K。
第四步,判断若 Zj(I+1)≠Zj(I),j=1,2,...,K,则将I+1赋值给I,返回第二步;否则,算法结束。
笔者的K均值聚类算法采取成批处理法进行初始分类的选取和调整,代表点就是聚类中心,选一批代表点后,计算其它样本到聚类中心的距离,将所有样本归于最近的中心点,形成初始分类,再重新计算聚类中心。
2.2 K均值集成聚类
2.2.1集成学习
集成学习是利用几个学习器进行综合学习。先选定几个个体学习器,然后使用一些结合方法进行结合。很多经典的机器学习算法,如随机森林法等都是采用集成学习建立的。随机森林法由多个决策树算法集成,这种个体学习器称为基学习器。集成学习结构图如图1所示。
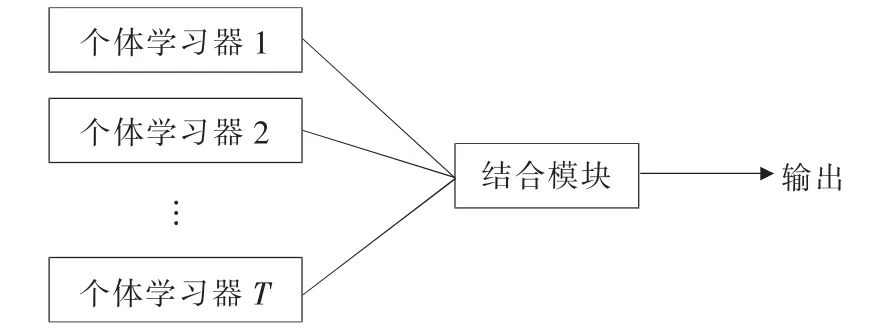
▲图1 集成学习结构图
2.2.2 Bootstrap
想要得到泛化性能强的集成,集成中的个体学习器应当尽可能相互独立。虽然独立在现实任务中无法做到,但可以设法使基学习器尽可能具有较大的差异。Bootstrap是统计学习中的一种重采样技术,这种看似简单的方法,对之后的很多技术都产生了深远影响。机器学习中的Bagging、AdaBoost等方法其实都蕴含了Bootstrap的思想。
在统计时,面临的只有样本,样本具有明显的不确定性。正因为不确定性的存在,才使统计能够生生不息,统计的意义也就在于基于样本推断总体。Bootstrap方法最初由美国斯坦福大学统计学教授Efron在1977年提出,作为一种崭新的增广样本统计方法,Bootstrap方法为集成学习的采样提供了很好的思路。
2.2.3 Bagging
Bagging是并行式集成学习方法中最著名的代表。给定样本容量为n的数据集,先随机取出一个样本放入采样集中,再将样本放回初始数据集,使下次采样时该样本仍有可能被选中,这样经过v次随机抽样,得到含v个样本的采样集。初始训练集中有的样本在采样集中多次出现,有的则从未出现。重复抽样过程T次,则得到T个样本容量为v的Bootstrap样本,记为Di=(x1,x2,...,xv),i=1,2,...,T。
采样出T个含v个训练样本的采样集,然后基于每个采样集训练出一个基学习器,再对这些基学习器进行结合,这就是Bagging的基本流程。在对结果进行输出结合时,Bagging通常使用投票原则。
2.2.4 K均值集成聚类算法
K均值聚类算法在机器学习中属于无监督学习,即使用没有标签的数据进行学习。集成学习使用多个基学习器来降低模型泛化误差中的偏差和方差。将以上两个概念结合起来,就是无监督集成学习,即对没有标签的数据使用集成算法。
将K均值与Bagging结合,生成K均值集成聚类算法,算法具体流程如图2所示。

▲图2 K均值集成聚类算法流程
第一步,按Bootstrap方式,对初始训练集进行v次有放回的随机抽样,重复T-1次抽样过程,采样出T-1个含v个训练样本的Bootstrap采样集,记为Di=(x1,x2,...,xv),i=1,2,...,T-1。
第二步,由于存在未被抽样的样本,因此当每个样本都需要归类时,需要将剩余所有未被抽样的w个样本取出,组成最后一个采样集,记为 DT=(x1,x2,...,xw),则总的采样集记为:
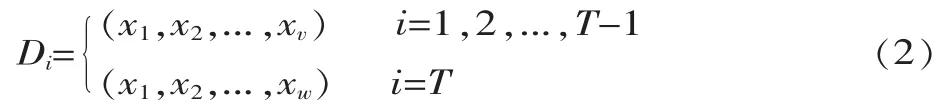
第三步,将T个采样集分别用K均值基学习器来单独进行聚类训练,设初始训练集样本数为z,聚类类别数为K,建立一个z·K维矩阵,用于记录每个个体学习器对每个样本聚类类别的投票情况,第i行第j列的数字s表示有s个基学习器将第i个样本归类为第j类。
第四步,根据建立的z·K维矩阵,按照投票法则来决定每一个样本的最终聚类类别。样本的最终类别由票数最多的类别决定,若存在投票数相同的类别,则在其中随机选择一个类别作为该样本最后的聚类类别。
3 双目标装配线平衡优化数学模型
笔者在工作站数固定和作业元素优先关系的约束条件下,将装配线生产节拍和平滑因子作为优化目标,建立双目标装配线平衡优化模型。
3.1 约束条件
C为生产节拍,I为作业元素集合,J为工作站集合,n为作业元素个数,mi为种群中第i个个体的实际工作站数目,M为确定的工作站数,Jk为第k个工作站的作业元素集合, k∈(1,M)。
x为一维向量,表征各装配作业元素排序情况,若x=[x1,x2,...,xn], 满足所有约束条件的 xi即为可行解。X为n·M维矩阵,表征各装配作业元素在工作站上的分配情况,对于 X(i,k)∈X,若 X(i,k)=1,则表示装配作业元素 i分配在工作站 k;若 X(i,k)=0,则表示装配作业元素i未分配在工作站k。PPred为n×2维优先关系集合,PPred(i,1)是 PPred(i,2)的前序作业元素。 P 为 n·n维优先关系矩阵,对于 P(k,i)∈P,若 P(k,i)=1,则表示 k 为 i的前序作业元素;若 P(k,i)=0,则表示 k 为 i的后序作业元素。ti为第i道作业元素的作业时间。
在企业实际生产中,装配线常常已经建立完毕,若改建或扩建,则成本高昂,所以工作站数是一定的。
每个作业元素只能分配到一个工作站上,即:
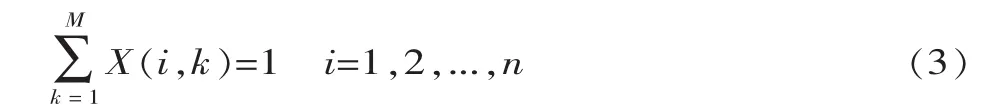
要在满足优先关系的条件下分配作业元素,即:
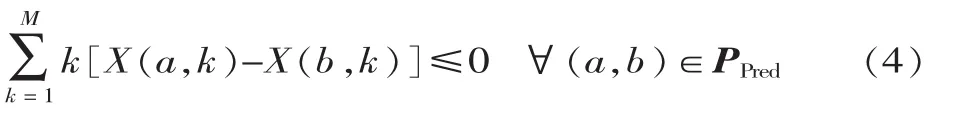
各工作站的作业总时间小于等于生产节拍,即:
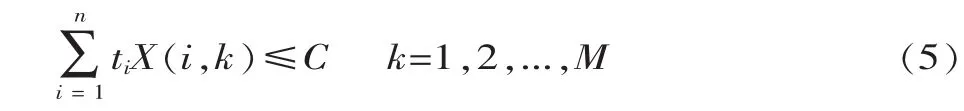
工作站数是一定的,即:
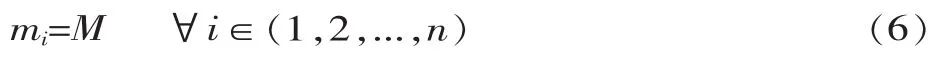
3.2 优化目标
笔者选择优化目标为生产节拍C和平滑因子SI,因为减小生产节拍C能起到缩短总空闲时间的作用,而平滑因子SI是评价装配线负荷平衡的指标,负荷平衡的作用是提高人员和设备利用率。优化目标定义为min C ,min SI。
其中,生产节拍C的定义是工作站作业时间的最大值,T(k)为第k个工作站的作业时间,则有:

平滑因子SI为:

3.3 数学模型
综合约束条件和优化目标,定义如下数学模型:
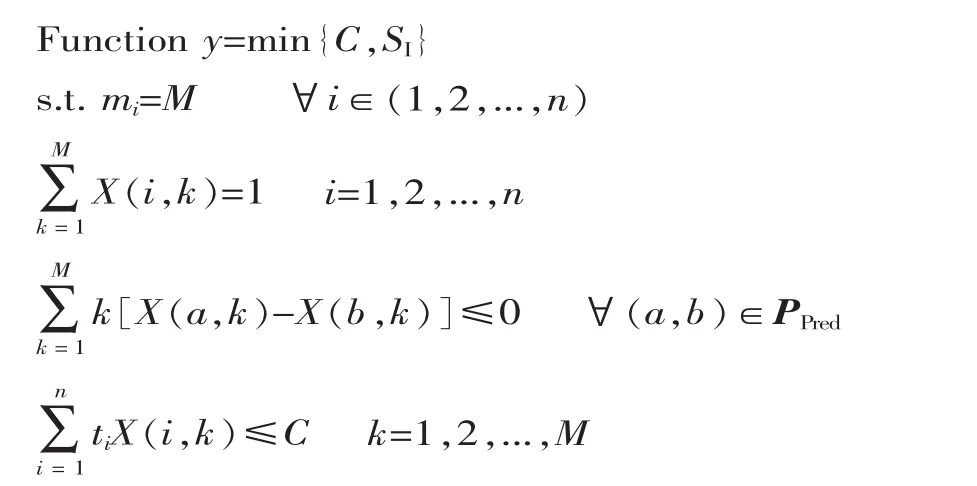
4 基于Bagging集成聚类的改进遗传算法
为提高遗传算法的搜索深度,笔者基于Bagging集成聚类算法的种群聚类分析方法,对遗传算法的交叉部分进行改进,判断随机配对的两个体是否是属于同一族群的近亲,避免近亲个体交叉。
4.1 算法流程
记Spop为种群数目,要求是2的倍数,Ppop(t)为第t代种群,G为遗传代数,Pc为交叉概率,Pm为变异概率,其余参数定义同前,则改进遗传算法流程如下。
第一步,初始值设定。 输入 Spop、G、C、M、Pc、Pm、T、v、K 的值。
第二步,初始化种群。令t=0,随机产生满足约束、数量为 Spop的初始种群 Ppop(0)。
第三步,适应度计算。对第t代种群Ppop(t)中每个个体计算适应度参考值,即染色体的生产节拍C和平滑因子SI。
第四步,惩罚策略。检查种群中的个体是否满足约束条件,若不满足工作站数固定为M的约束,则给此个体适应度一个惩罚项,将两个适应度参考值变为某极大值,如500。
第五步,双目标并列选择操作。根据两个适应度参考值,分别选出两个适应度参考值最优的s个个体,s=Spop/2,然后重组为新种群,作为第t+1代种群。
第六步,交叉操作。利用Bagging集成聚类算法对交叉规则进行改进,交叉形式采用单点交叉。
第七步,变异操作。变异规则采用单点变异。
第八步,循环。将t+1赋值给t,如果满足停止条件,结束;否则转向第三步。
4.2 编码与策略
在满足作业元素优先关系的约束条件下,对所有作业元素进行排列。每个作业元素对应染色体的一个基因位,排列好的个体记为一条编码染色体。
在交叉变异后,对种群中的个体重新做约束检查。若某个体不满足工作站数固定的条件,则对该个体的两个适应度参考值生产节拍C和平滑因子SI给予一个惩罚项,如500。由于惩罚项较大,因此被惩罚的个体容易在选择环节淘汰。
对第t代种群Ppop(t),根据计算好的每个个体适应度参考值生产节拍C和平滑因子SI,独立选出最优的前1/2个体,然后组成新的第t+1代种群。
4.3 交叉操作
遗传算法中,个体以编码形式存在,可以将各编码值看作个体的特征值,用聚类方法来判断两个体是否属于近亲。K均值属于硬聚类,是一种弱学习器,学习效果有限。将多个K均值进行结合,则得到超越个体学习器的优越泛化性能。笔者通过之前建立的基于Bagging的K均值集成聚类方法改进遗传算法的交叉操作。
由交叉概率 Pm决定第t代种群 Ppop(t)发生交叉的概率,交叉具体规则为单点交叉,具体如下。
第一步,将排序打乱,随机配对。
第二步,对第t代种群Ppop(t)中所有个体,采样出T个含v个训练样本的采样集。将剩余所有未被抽样的w个样本作为最后一个采样集,对采样集进行Bagging K均值集成聚类算法,聚类类别数为K,根据投票法则得到每个个体的聚类类别。
第三步,对比随机配对的两个体所属的聚类类别,若两者属于同一类别,则当前两个体不交叉,跳过,进行下一组;否则,两个体进行交叉,交叉采用单点交叉规则。
5 实例分析
为了验证笔者算法的深度搜索能力,以某汽车变速箱装配线为实例,对该条装配线进行平衡优化。汽车变速箱装配体由三个主要部分组成,作业元素数量n=27,优先关系如图3所示。装配线的工作站已建立好,工作站数M=12,若改建或扩建,则成本高昂。
对该装配线进行平衡优化,在工作站数固定为M=12的约束下,以生产节拍C和平滑因子SI为优化目标,利用提出的改进型遗传算法进行求解,提高搜索深度。
5.1 双目标优化求解
利用MATLAB 2015b编程求解,数学模型的参数设定如下:固定工作站数M=12,交叉概率Pc=0.6,变异概率Pm=0.05,遗传代数 G=50,种群数量 S=200,生产节拍初始值C=130 s。
当设定T=5、v=60、K=3时,生产节拍C和平滑因子SI的优化过程分别如图4和图5所示。优化过程记录了每代种群中C和SI的最优值。
由图4和图5可知,两个目标都得到了优化。生产节拍优化比较容易,在5代以内得到最终优化值。平滑因子在不断优化,在40代后收敛,没有过早收敛。选取一些具有代表性的优秀解,见表1、表2。

▲图3 汽车变速箱装配优先关系
由表1、表2可见,生产节拍C和平滑因子SI两个目标均得到了优化,提高了装配效率,减少了总空闲时间,算法对可行解进行了深度搜索,优化出多个较优解。
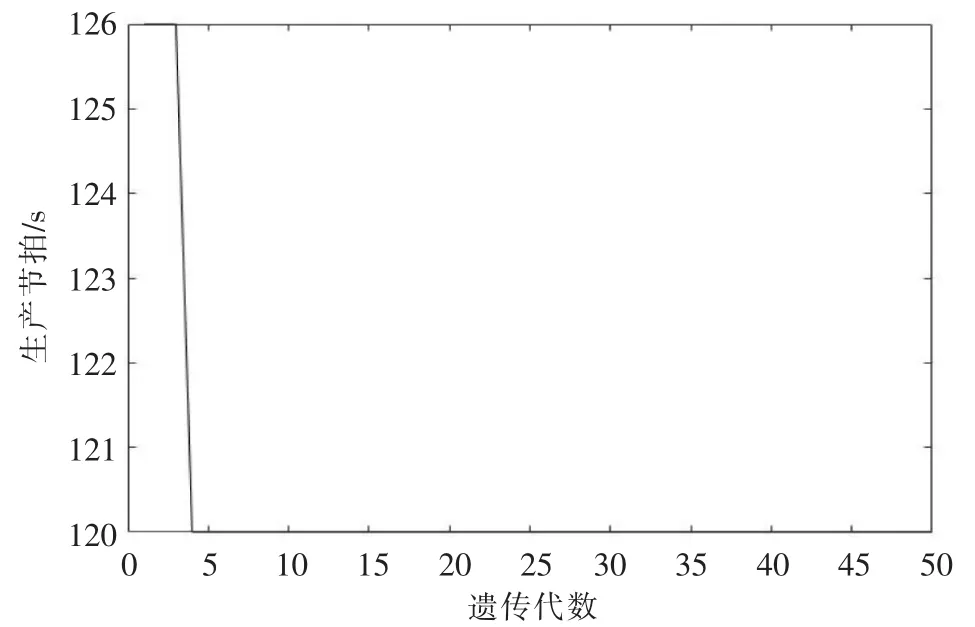
▲图4 生产节拍优化过程
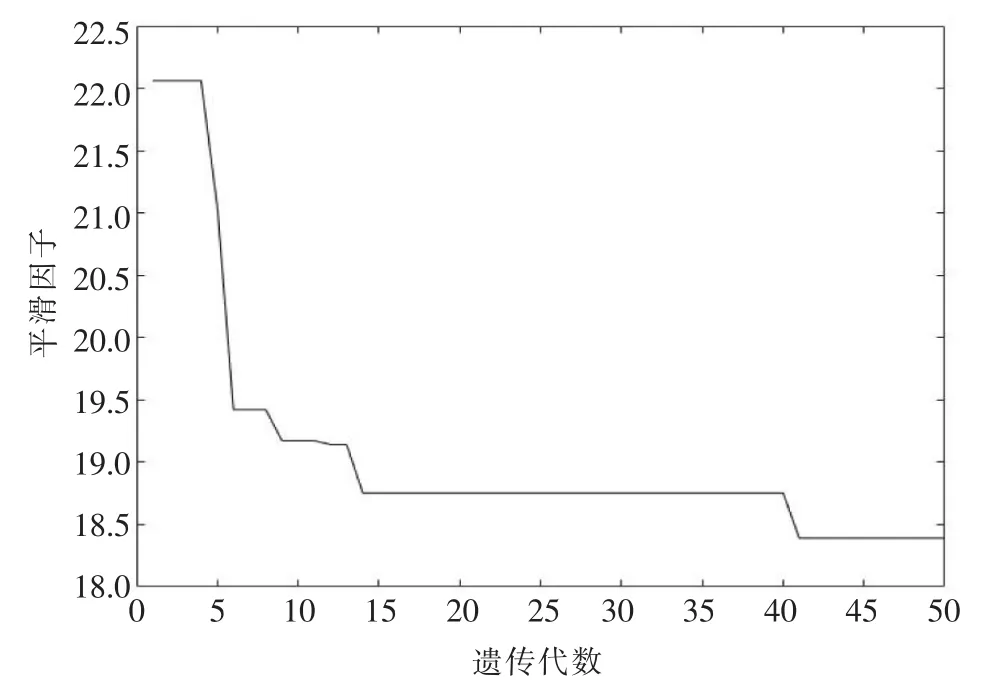
▲图5 平滑因子优化过程

表1 作业元素分配方案1
5.2 方案对比
基于Bagging集成聚类的改进遗传算法在不同主要参数设置时,搜索深度会有差异,主要参数包括T、v和K。为证明改进后的遗传算法搜索深度确实有提升,对参数进行不同设置,做对比试验。一是给定不同的T、v、K进行优化,二是利用未改进的遗传算法进行求解。进行多组对比试验,取两个目标数值之和最小的解为代表,对比结果见表3。

表2 作业元素分配方案2
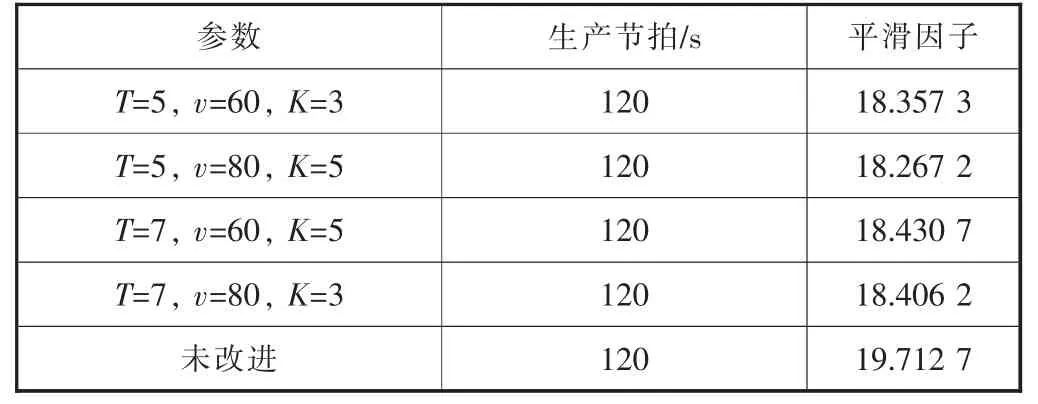
表3 方案对比
由表3分析可知,每组试验得到的平衡方案中生产节拍C优化解都相同,而平滑因子SI则不相同,这说明从单一的优化目标角度来看,生产节拍的优化较为容易,平滑因子的优化则较难,不同参数设置下得到的搜索深度不同。对比各组试验结果,用改进遗传算法求出的优化解在不同参数设置下的结果并不相同,搜索深度有差别;整体上,用改进遗传算法求出的优化解明显优于未改进遗传算法。综上所述,基于Bagging集成聚类的改进遗传算法,相比未改进的遗传算法,搜索深度更深,能得到更优的解。
6 结束语
笔者从生物学中近亲不能交叉的角度考虑,建立了一种基于Bagging集成聚类算法的种群聚类分析方法,利用这一方法判断种群中的两个体是否属于近亲,进而改进了遗传算法的交叉规则。以生产节拍和平滑因子为优化目标,建立了双目标装配线平衡模型,将改进遗传算法应用于双目标装配线平衡实例中。实例显示,改进遗传算法相比未改进遗传算法,有效提升了算法的深度寻优能力。
[1] 窦建平,苏春,李俊.求解第Ⅰ类装配线平衡问题的离散粒子群优化算法[J].计算机集成制造系统, 2012, 18(5):1021-1030.
[2] 郑巧仙,李元香,李明,等.面向第Ⅱ类装配线平衡问题的蚁群算法[J].计算机集成制造系统, 2012, 18(5):999-1005.
[3] 张子凯,唐秋华,张利平,等.改进遗传算法求解大规模混流 U型装配线问题 [J].机械设计与制造,2016(1):137-139.
[4] 梁雨生,李向波.基于遗传算法的装配线平衡问题研究[J].价值工程, 2013, 32(5):123-125.
[5] 扈静,蒋增强,葛茂根,等.基于改进遗传算法的混合装配生产线平衡问题研究[J].合肥工业大学学报(自然科学版),2010, 33(7):1006-1009.
[6] 董双飞.基于改进遗传算法的混流装配线多目标平衡优化研究[D].重庆:重庆交通大学,2015.
[7] 李险峰.基于改进遗传算法的汽车装配生产线平衡问题研究[D].北京:北京科技大学,2017.
[8] 韩煜东,董双飞,谭柏川.基于改进遗传算法的混装线多目标优化[J].计算机集成制造系统, 2015, 21(6):1476-1485.
[9] 刘雪梅,兰琳琳,顾佳巍,等.基于工位复杂性测度的随机型装配线平衡优化方法 [J/OL].计算机集成制造系统,http://kns.cnki.net/KCMS/detail/11.3619.TP.20170627.1615.006.html.
[10]陈星宇.基于改进遗传算法的装配生产线平衡技术研究[D].上海:上海交通大学,2011.
[11] HOU L,WU Y M,LAI R S,et al.Product Family Assembly Line Balancing Based on an Improved Genetic Algorithm[J].The International Journal of Advanced Manufacturing Technology, 2014,70(9-12):1775-1786.
