基于层次聚类的机加工线平衡优化*

□ 李爱平 □ 傅 翔 □ 刘雪梅

同济大学机械与能源工程学院 上海 201804

1　研究背景

生产制造企业为满足客户对于交货期的需求，期望以最短的时间加工出高质量的零件。因此，节拍与平衡率成为衡量生产线优劣的主要技术指标。线平衡问题自1955年由Salveson［1］第一次提出以来，一直都是热点问题，业内诸多专家学者及工程技术人员都对其进行了研究。但由于线平衡问题的复杂性，即使最简单的问题也都属于非确定多项式难题［2］，且大规模线平衡问题尤其复杂，因此仍需寻求较为便捷的方法解决该问题。

文献［3］针对柔性加工线平衡问题，提出了工位配置、操作分配与排序的方法，这一方法考虑了多种约束条件，通过设计多目标算法获得了较优解。文献［4］通过应用基于贪婪随机自适应搜索算法的启发式算法来优化可重构机加工线多目标平衡问题，取得了不错的成果，但这一方法只适用于加工操作数较少的情况。文献［5-6］针对机加工线平衡问题，提出了混合整数规划的数学模型及基于贪婪随机自适应搜索算法的启发式算法，处理大规模生产线的平衡问题，但存在算法复杂、收敛较慢、效率较低等问题。文献［7］等在COMSOAL技术和回溯方法论的基础上，提出了一种启发式算法，考虑特征之间的加工优先级和兼容性约束关系，针对机加工线中各装夹下的加工元聚类排序问题，在减少主轴头和工作站数量的同时，获得了比较理想的节拍和平衡率，这一方法在求解大规模机加工线平衡问题时表现出较优的特性。文献［8］以减少设备数量为目标，将加工操作进行分模块处理，并将其按一定的约束条件合理分配至各个机床，同时研究了几种较优算法对不同特征操作数量的优化结果，从而得出在一定范围内适宜采用的算法。

可见，尽管国内外诸多学者都对线平衡问题进行了大量研究，也取得了较为丰硕的成果，但在求解大规模机加工线平衡问题时，仍存在算法复杂、求解效率较低等问题。笔者在总结之前研究的基础上，提出一种基于层次聚类处理的加工元聚类方法，将加工元分为不同组单元，并应用改进的遗传算法进行优化求解。

2　问题描述

生产复杂零件时，由于待加工操作较多，一次装夹难以完成全部加工，因此需要分多个工位依次加工，每个工位配备相应数量的机床，并使各工位以一个统一的节拍串行工作。柔性机加工生产线平衡指将需要加工的操作按一定的约束关系，以特定的方式分配至各工位，进而达到节拍最短、辅助时间最短、平衡率最高等优化目标。

2.1　加工元模型

通常，零件都由携带加工信息的特征所组成，若一个零件由m个特征组成，则由这m个特征组成零件的加工特征集F可表示为：

式中：fi为零件的第i个特征元。

由于每个特征元对应一种或多种加工方法链，而每种加工方法链又由多个元素组成，因此笔者将这样的元素称为加工元，则零件的加工序列可以表示为：

式中:Oi为第i个加工元；n为加工元总数。

为完整表示加工元的属性，笔者引入五维向量Oi=｛WID，WTool，WFix，WTAD，WTime｝，WID为加工操作编号，WTool为所采用的刀具，WFix为所采用的夹具，WTAD为该加工操作所在工位刀具可进刀的方向，WTime为加工时间。

对于每一个加工元，都有以下约束：① 一个加工元属于且仅属于一个特征元；②一个加工元属于且仅属于一个加工阶段；③一个加工元属于且仅属于一个工位；④一个加工元有且仅使用一把刀具；⑤ 一个加工元属于且仅属于一个装夹。

2.2　约束模型

2.2.1 工艺约束

加工元分配时需要遵循一定的工艺约束准则，这样才能保证零件的加工质量，取得良好的经济效益。根据加工元之间的强弱关系，可分为强制性约束与经济性约束两大类。

强制性约束指加工零件时必须严格执行的约束，如先面后孔、先粗后精、先基准后其它、先主后次等。经济性约束指在加工过程中只对加工经济产生影响的约束，加工元违反经济性约束不会对零件加工质量产生影响。

2.2.2 装夹约束

零件加工时需要利用夹具对其进行定位夹紧，以便刀具准确定位加工。由于夹具的遮挡，使一些特征不能被刀具加工，因而产生了装夹约束。

2.2.3 工位约束

为取得良好的平衡效果，将加工元分配至各工位时，需满足工位时间约束：

式中：T0为理论节拍，由企业生产纲领决定；TP（k）为 k工位限制分配时间；M（k）为k工位配备的机床数。

总机床数M为各个工位机床数之和：

2.2.4 其它约束

此外，还有一些其它约束，如包含约束与不包含约束。包含约束要求某些加工元必须在一次装夹下完成加工，不包含约束要求某些加工元不能在同一装夹下加工，需分工位加工。

2.3　优化目标

节拍及平衡率作为评价企业生产效率的主要技术指标，其重要性不言而喻。笔者以节拍和平衡率为主要优化目标，寻求整线节拍CT最小化、平衡率Bp最大化：

式中：Ti为工位i的节拍；Tsum为加工零件所需的总时间。

3　层次聚类处理

聚类分析是指在无引导的条件下，应用数学方法研究和处理所给对象的分类及各类之间的亲疏程度。笔者应用层次聚类方法对样本集合进行合并，直到满足终止条件，完成聚类处理。

3.1　零件聚类模型

对于零件加工元集合 P=｛O1，O2，...，Oi，...，On｝，聚类的目的是将加工元按照约束关系及某种属性关系分为 K 类，C=｛C1，C2，...，CK｝（K≤n）， 这 K 类需满足：①Ci≠i=1，2，...，K；②Ci=｛C1，C2，...，CK｝；③ Ci∩Cj=，i，j=1，2，...，K 且 i≠j。

为确定待聚类加工元间的相近关系，需度量加工元间的相似程度或非相似程度，再用适当方法进行聚类分组，建立分类谱系图。聚类分析方法通常使用相似因数（向量夹角余弦）和欧氏距离因数等作为分类统计量。

3.1.1 相似因数

设输入数据空间Rm中n个样品定量观测数Xα=（xα1，xα2，...，xαm）T，α=1，2，...，n，定义相似因数衡量样品之间的相似程度：

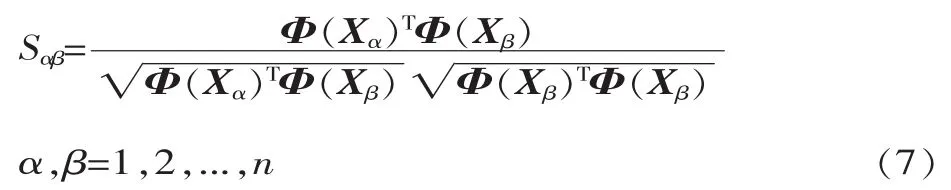
式中：Sαβ为相似因数，即 α、β 两个样品向量 Φ（Xα）和Φ（Xβ）之间的夹角余弦，并且具有对称性，Sαβ=Sβα，Sαβ∈［-1,1］。

3.1.2 欧式距离因数

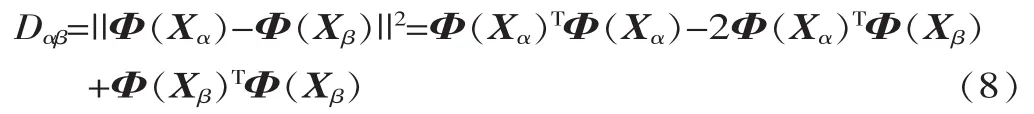
式中：Dαβ为 α、β 两样品向量 Φ（Xα）和 Φ（Xβ）之间的欧式距离二次方，Dαβ同样具有对称性，Dαβ=Dβα。

3.2　加工操作之间相似度的计算

笔者采用相似度s表示两加工元之间的相近关系。与一般的聚类方法不同，装夹规划的加工单元之间存在各种约束关系，因此此处采用一种启发式方法进行聚类处理。

在聚类处理中，相似度越大表示加工元之间相似程度越高，越适合在同一装夹下加工。定义相似度s由两部分组成，即 s=（s1，s2），其中 s1为待聚类的加工元必须满足制造资源加工能力约束，s2为加工元间的位置公差，两者进一步表征了加工元之间的亲疏关系。

3.2.1相似度s1

规定相似度 s1由四部分组成， 即 s1=（s11，s12，s13，s14）。

s11为两加工元所使用的机床设备相似度，若Oi与Oj都能在同一机床设备上加工，则s11=1，否则s11=0。

笔者使用的是卧式四轴加工中心，其生产能力范围见表1。

表1　卧式四轴加工中心生产能力范围

s12为两加工元间的加工刀具相似度，当加工元Oi与Oj使用相同型号规格的刀具时，s12=1，否则s12=0。

s13为两加工元间的加工方位面相似度，当加工元Oi与Oj具有相同的可加工方向时，s13=1，否则s13=0。

s14对应于工艺约束中强制性约束的定位与基准约束，表示加工元间的定位基准关系相似度。规定当加工元Oi与Oj具有相同的定位加工基准时，s14=1，否则s14=0。

3.2.2 相似度s2

相似度 s2由两部分组成，即 s2=（s21，s22）。

s21为两加工元间的形位公差关系，当加工元Oi与Oj间具有形位公差时，s21=1，否则s21=0。

s22为切削力大小，主要针对精度高、需要分阶段加工的特征操作。当零件加工精度要求高或刚度差时，对零件的某些特征需分阶段进行，粗加工与精加工的参数设置不同，切削力大小相差较大，此时若将不同加工阶段的加工元聚合到一起，容易引起零件切削变形量增大。规定当加工元Oi与Oj属于同一个加工阶段时，s22=1；当加工元Oi与Oj分别属于精加工与粗加工时，s22=0；当加工元Oi与Oj分别属于半精加工与粗加工或半精加工与精加工时，s22=0.7。

3.2.3 相似度s

从2.2节可知，约束分为强制性约束和经济性约束，在进行加工元间的相似度s计算时，s1是针对强制性约束设定的，s2是针对经济性约束设定的。对于相似度s，可以采用加权处理，计算式为：

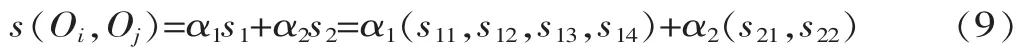
考虑到强制性约束对于聚类的重要性，设定α1=10，α2=1。

3.2.4 加工操作相异度矩阵

由式（9）相似度计算公式，分别计算两两加工元间的相似度值，并将其存入下三角矩阵，得到相异度矩阵SN×N：

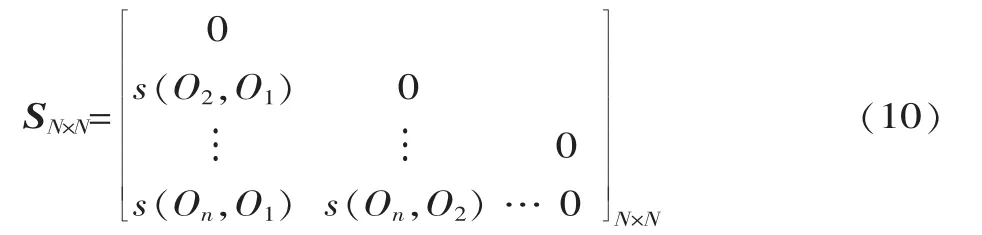
3.3　基于不同阈值的操作聚类

通过相异度矩阵计算出两两加工元间的相似度，将其聚合后组成加工元段。聚类的粒度粗细需控制适当，若粒度过细，则聚类后的加工元种类仍然较多，不能起到降低问题规模的目的；若粒度过粗，则问题的某些性质被模糊，聚类后加工元种类的多样性降低，影响算法求解的解空间。可见，聚类分析的阈值设置显得尤为重要［9］。

笔者采用基于凝聚的层次聚类法，将操作段数目控制在某个合适区间内。

（1）按公式计算零件所有加工元间的相似度s（Oi，Oj）。

（2）根据相似度s生成加工元间的相异度矩阵SN×N。

（3）设定阈值σ，根据相异度矩阵，将矩阵内的元素按数值从小到大进行排列 σ1＜σ2＜σ3＜...＜σn。 分别设定阈值 σ=σ1，σ2，．．．，σn，针对不同阈值得到不同层次的聚类结果，其中r为操作段的编号，σn为该操作段的阈值。

（4）依据启发式方法进行加工操作分组。

（5）进行单元组内排序。

按这一聚类方法，可对发动机缸体零件各个方位面上的加工元进行聚类处理，以减小问题规模。

4　遗传算法

遗传算法是一种通过模拟自然界物种进化过程，寻求全局最优的随机搜索算法，具有较强的鲁棒性和通用优化能力，广泛用于求解各类复杂问题。笔者对传统遗传算法进行优化改进，将其应用于求解线平衡优化问题。

4.1　编码

为简化算法运算，笔者对每一个加工元进行编号，采用加工元序列号编码方式，将加工元排列为一个向量，作为一个染色体。

4.2　解码

解码过程即产生解方案的过程，笔者按照各工位装夹约束及时间约束，将加工元序列编号分配至各工位，产生最终解方案。

4.3　选择

选择算子采用轮盘赌选择方式，有助于将适应度值较大的个体保存下来。

4.4　交叉变异

遗传算法的交叉变异概率是影响算法性能的关键，直接影响算法的收敛性。笔者通过引入自适应策略对交叉变异算子进行优化改进，以避免算法早熟现象的产生。交叉概率Pc和变异概率Pm按如下公式进行自适应调整：

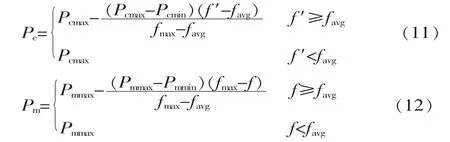
式中：Pcmax、Pcmin为交叉概率的上下限；Pmmax、Pmmin为变异概率的上下限；fmax为种群的最大适应度；favg为种群适应度平均值；f′为参与交叉的两个个体中较大的适应度；f为参与变异的两个个体中较大的适应度。

4.5　初始种群

随机生成yPop个个体组成初始种群。每一个个体按加工元之间的强制性约束和经济性约束分配至各工位，这样不仅满足各种约束关系，而且具有较高的初始平衡率。

5　算例

5.1　实例描述

笔者以某企业发动机缸体柔性生产线为例，进行线平衡优化。该企业现有卧式四轴加工中心9台，夹具由专业夹具厂商合作生产。

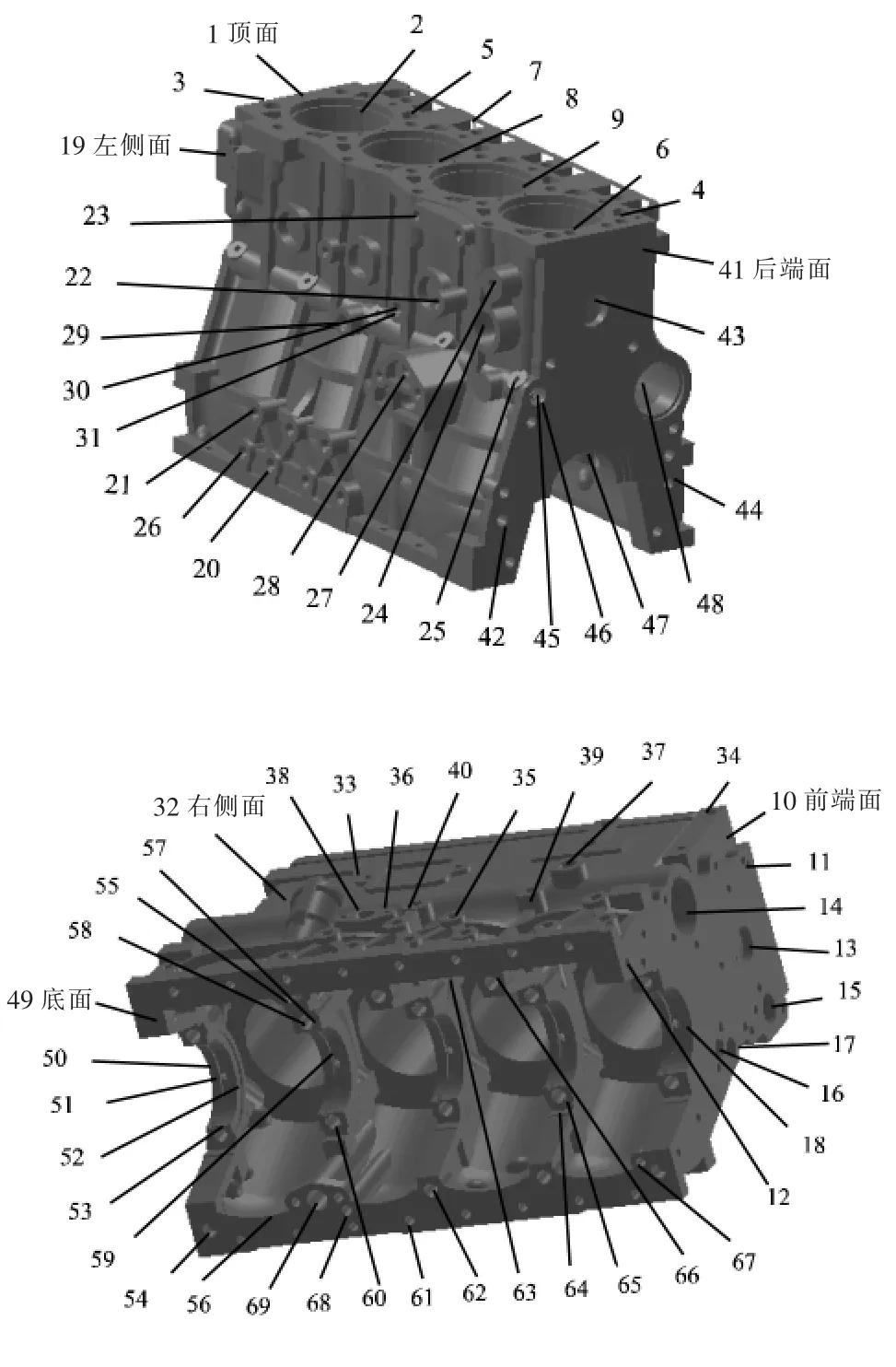
▲图1 缸体三维模型及加工特征

图1为发动机缸体三维模型及其加工特征。表2为缸体顶面加工元信息。根据前文所述，已将同一类型操作聚为一类，如表2中4个缸套孔合并为一个加工单元。经初步统计，该缸体零件共有69个加工特征、149个加工元。在此基础上，再进行层次聚类处理。限于篇幅，笔者以缸体顶面为例进行聚类分组。

5.2　层次聚类处理

5.2.1 计算各加工元相似度

由表2可知，加工元O1与O2均可使用卧式四轴加工中心加工，s11=1；刀具相同，s12=1；进刀方向一致，s13=1；定位基准相同，s14=1；由于两者不存在公差关系，s21=0；顶面粗精铣分属于粗加工与精加工，s22=0。加工元O1与O2的相似度可根据式（9）计算得到：

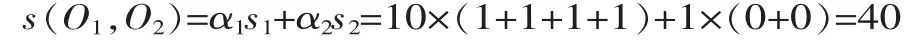
同理，可得其它加工元间的相似度：

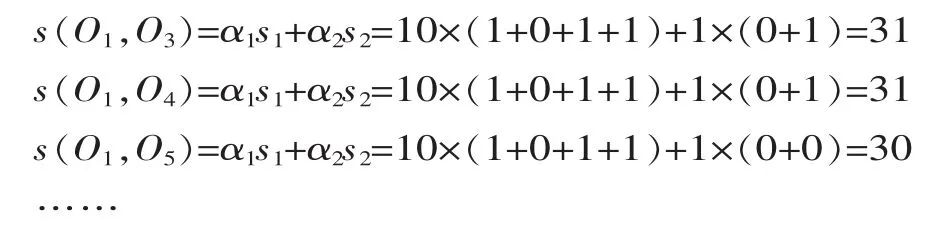
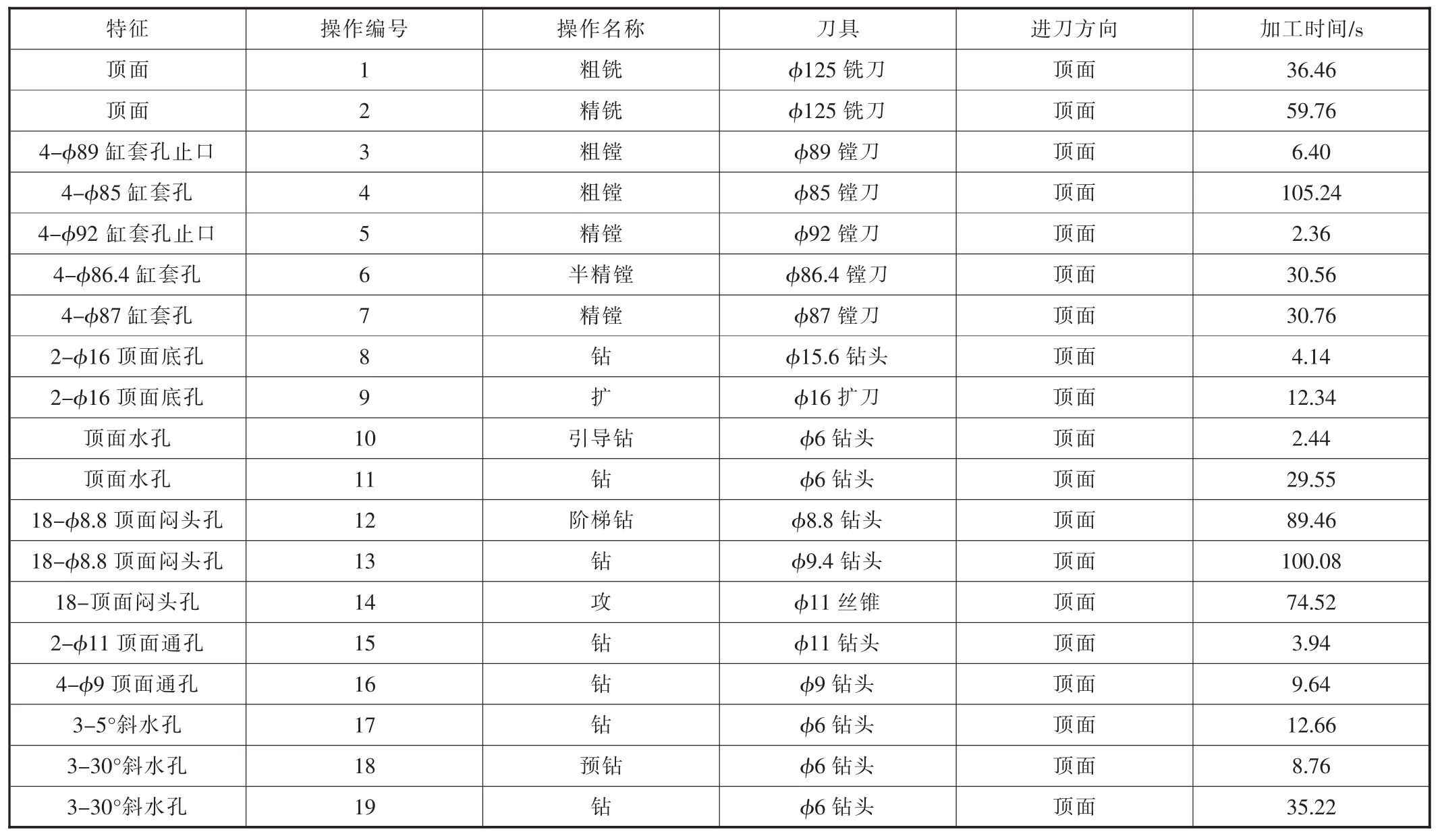
表2　缸体顶面加工元信息

5.2.2 顶面相异度矩阵

将上述所求相似度值输入相异度矩阵S19×19：

5.2.3 阈值

遍历相异度矩阵，可得其相似度值处于0～41区间范围内，按从小到大排列为 0＜30＜30.7＜31＜32＜41。 依次按照相似度值设定相应的阈值，得到最优加工单元组为：=｛O1，O8，O10，O11｝，=｛O2，O5，O6，O7｝，=｛O3，O4｝，=｛O9，O12，O13，O14｝，=｛O15，O16｝，=｛O17，O18，O19｝。

5.3　算法求解

5.3.1 参数设置

笔者设置如下：yPop=30，Pcmax=0.6，Pcmin=0.1，Pmmax=0.07，Pmmin=0.01，迭代次数 Gmax=300。

5.3.2 遗传算法对比

分别应用改进后的遗传算法与传统遗传算法对这一问题进行求解，如图2所示。对比图2发现，改进后的算法收敛速度更快，效率更高，优化目标更佳，只需90次迭代便能找到最优解，而传统遗传算法要经过164迭代才能找到最优解。

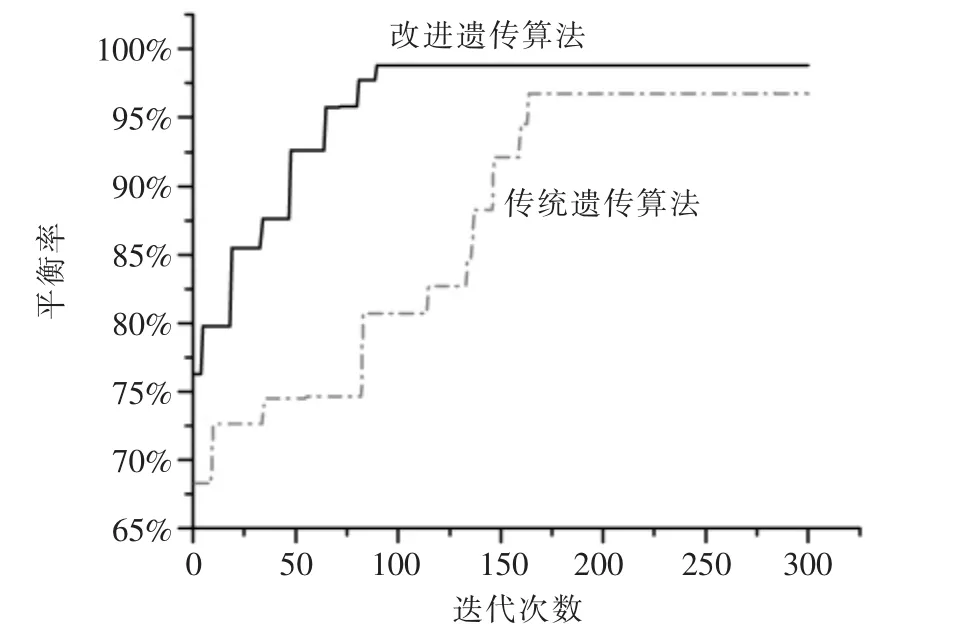
▲图2 遗传算法对比

5.3.3 结果分析

算法运行50次后，得到最优解方案，见表3。该方案中，生产节拍为539.44 s，平衡率高达98.78%，工位数为6，其构型方案如图3所示。笔者算法所得方案与企业自身规划方案对比见表4，可以发现笔者的算法方案节拍缩短33.68 s，平衡率提高7.88个百分点。

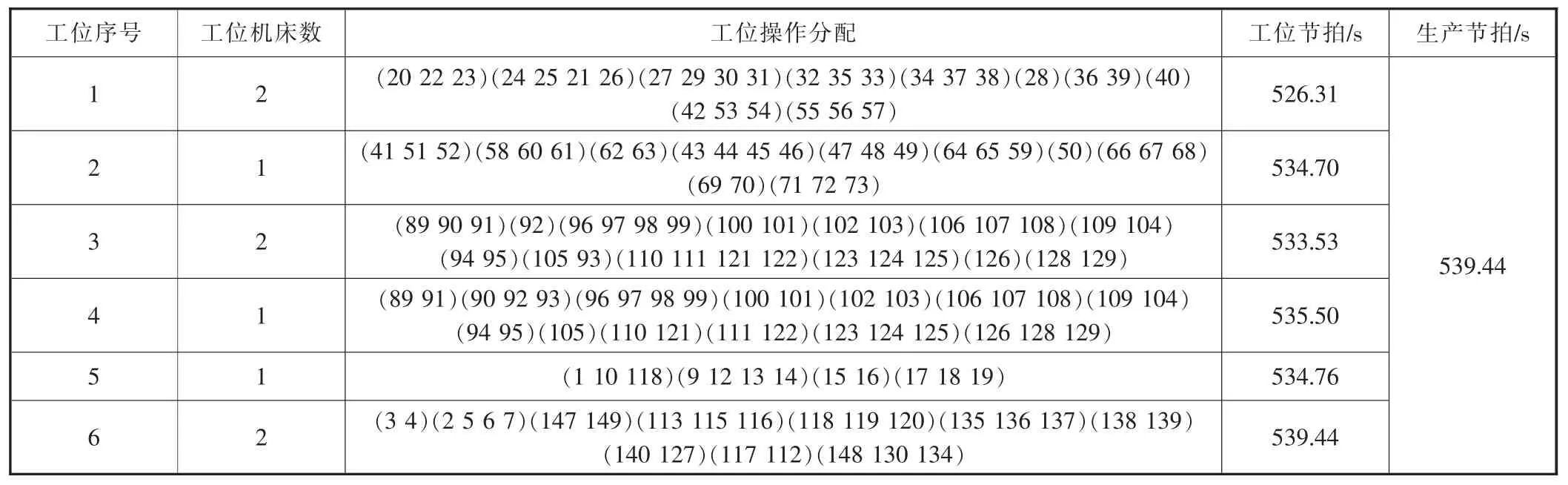
表3　最优解方案

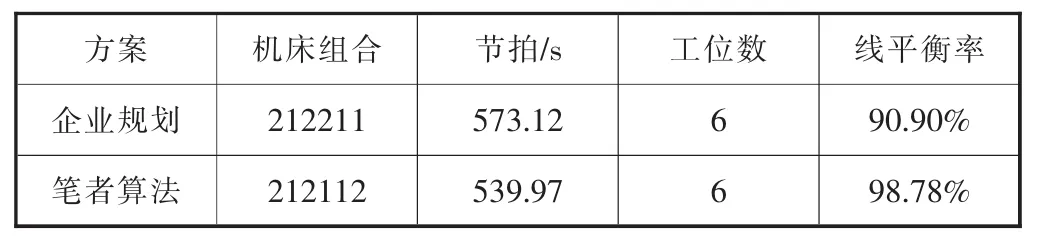
表4　方案对比

▲图3 最优构型方案

综上所述，应用层次聚类方法对加工元聚类分组，有效减少了加工元的种类数量，降低了问题求解的规模与难度。基于交叉变异算子自适应的改进遗传算法在求解线平衡问题中优势明显，不仅收敛速度更快，所求目标值更佳，而且可以有效降低生产节拍，提升线平衡率，对于提高企业市场竞争力具有较大帮助。

6　结语

笔者针对现有方法在求解大规模机加工线平衡问题时存在算法复杂、效率较低等问题，提出了一种针对发动机缸体类零件加工特征的层次聚类方法。首先对零件特征进行转化，以加工元为最小单位，构建加工元先后约束、工艺约束、装夹约束及工位约束；然后以节拍、平衡率为优化目标，建立了基于层次聚类的线平衡问题求解模型；接着对交叉变异算子采用自适应策略，改进了传统遗传算法，从而加快了算法运行效率，有效避免算法陷入早熟，提升了解搜索空间；最后以某企业发动机缸体生产线为例，将分组后的加工单元组分配至各工位，达到了较好的平衡效果，对于指导企业生产具有重要的实际意义。

［1］ SALVESON M E.The Assembly Line Balancing Problem［C］.Proceedings of the Second Symposium in Linear Programming，Washington D C，1955.

［2］ TANG Q H，LI Z X，ZHANG L P，et al.Effective Hybrid Teaching-learning-based Optimization Algorithm for Balancing Two-sided Assembly Lines with Multiple Constraints［J］.Chinese Journal of Mechanical Engineering， 2015， 28（5）：1067-1079.

［3］ 刘雪梅，孟飞飞，李爱平，等.基于多色集合理论和遗传算法的加工中心工步排序研究［J］.中国机械工程，2013，24（18）：2437-2442.

［4］ DELORME X， MALYUTIN S， DOLGUI A.A Multiobjective Approach for Design of Reconfigurable Transfer Lines［J］.IFAC-PapersOnLine， 2016， 49（12）：509-514.

［5］ ESSAFI M，DELORME X，DOLGUI A.A GRASP Heuristic for Sequence-Dependent Transfer Line Balancing Problem［J］.IFAC Proceedings Volumes， 2009， 42（4）：762-767.

［6］ ESSAFI M， DELORME X， DOLGUI A， et al.A MIP Approach for Balancing TransferLine with Complex Industrial Constraints［J］.Computers&Industrial Engineering， 2010， 58（3）：393-400.

［7］ FINEL B， DOLGUI A，VERNADAT F.A Random Search and Backtracking Procedure for Transfer Line Balancing［J］.International Journal of Computer Integrated Manufacturing，2008， 21（4）：376-387.

［8］ GUSCHINSKAYA O， DOLGUI A.Comparison of Exact and Heuristic Methods for a Transfer Line Balancing Problem［J］.International Journal of Production Economics， 2009， 120（2）：276-286.

［9］ 王伦文.聚类的粒度分析［J］.计算机工程与应用，2006，42（5）：29-31.