圆锥滚子轴承受载过程内部载荷与接触应力研究

□ 魏延刚 □ 宋宇谟

大连交通大学机械工程学院 辽宁大连 116028

1　研究背景

滚动轴承依靠主要元件间的滚动接触来支承转动零件，广泛应用于各种机械设备中［1-2］。图1为圆锥滚子轴承的承载机理，无论是否施加外部轴向力，只要承受径向载荷R，承载区每个圆锥滚子所承受的法向反力Ni可分解为径向分力Pi和轴向分力Si。所有径向分力的合力与径向载荷R平衡，即∑Pi=R。而所有轴向力的合力∑Si=S，即为外部径向载荷对轴承产生的派生轴向力。

虽然轴承的派生轴向力大小由自身内部结构和所承受的径向载荷所决定，与外部轴向力无关，但是外部轴向力的大小是否会影响轴承载荷的分布，对承载区滚子的接触应力又有何影响，针对这些问题需要进行研究。

马书尧等［3-5］对圆锥滚子轴承在不同外部载荷作用下的内部载荷与应力进行了研究，得到了一些有价值的结果，但是这些研究均只是探讨完全加载后圆锥滚子轴承的内部载荷分布与接触应力，而对受载过程中圆锥滚子轴承的内部载荷与应力变化情况则没有进行研究。

笔者采用有限元方法对圆锥滚子轴承进行仿真分析，重点研究在施加外部径向载荷后，逐步施加外部轴向载荷对圆锥滚子轴承载荷分布与接触应力等的影响，从而对圆锥滚子轴承的设计和应用提供参考数据。

2　有限元建模

所研究的圆锥滚子轴承主要结构参数如下：轴承外径为215 mm，轴承内径为120 mm，轴承宽度为61.5 mm，滚子大端面直径为25 mm，长度为45.6 mm，半锥角为2°，滚子数为20。

根据接触力学的概念，考虑圆锥滚子轴承的结构和所受载荷对称的特点，取轴承1/2模型进行有限元分析。由于圆锥滚子轴承受径向载荷所产生的派生轴向力会推动轴承内圈与滚子分离，因此必须对轴承内圈进行轴向定位，于是在内圈外侧端面增加一个挡环，如图2所示。为了方便描述，对滚子进行逆时针编号，如图3所示。

轴承内外圈及滚子的材料均采用轴承钢，弹性模量为207 GPa，泊松比为0.3。由于轴承内部为油脂润滑，因此摩擦因数设为0.1。为了减少计算时间，且保证计算精度，网格划分的策略是对轴承整体进行网格粗化，在发生接触的区域进行网格细化［6-9］，圆锥滚子轴承网格模型如图4所示。在轴承的切分平面施加对称位移约束，轴承外圈圆弧面施加位移约束，轴承内圈只释放径向和轴向自由度，并在轴承内圈耦合点施加径向和轴向载荷［10］。

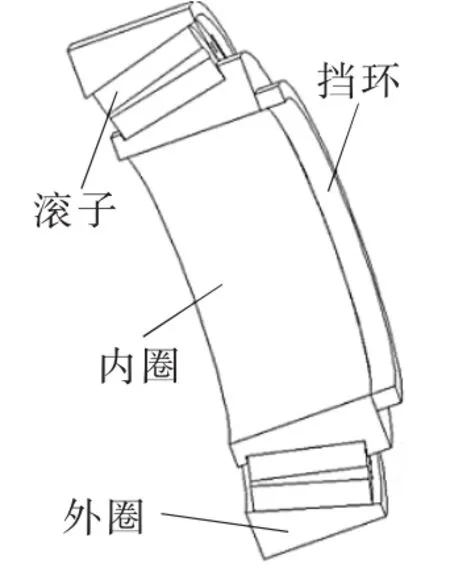
▲图2 圆锥滚子轴承结构

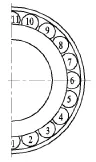
▲图3 滚子编号顺序

▲图4 圆锥滚子轴承网格模型

施加的外部径向载荷最大为80 000 N，外部轴向载荷最大为60 000 N。外部载荷由小到大逐渐施加至最大值，先施加径向载荷，由0到最大值；再施加轴向载荷，由0到最大值。笔者针对两种工况进行研究，一是所施加的外部轴向载荷与由外部径向载荷所产生的派生轴向力方向相反，二是所施加的外部轴向载荷与由外部径向载荷所产生的派生轴向力方向相同。

3　受载过程有限元分析

3.1　外部轴向载荷与派生轴向力方向相反

在逐渐施加径向载荷至80 000 N后，求得其派生轴向力为31 350 N，然后再逐渐施加外部轴向载荷至60 000 N，方向与派生轴向力方向相反。

图5为滚子与内圈之间的法向接触力随外部载荷逐渐增大的变化曲线。横坐标为施加载荷的时间段，a～c时间段内，线性增大施加径向载荷；c～e时间段内，与派生轴向力反向线性增大施加轴向载荷。纵坐标为滚子在接触面上所承受的法向接触力。1号滚子由于是半个滚子，因此有限元分析所得的接触力为实际值的一半。在a～c时间段内，各滚子所受的法向接触力随径向载荷的线性增大而线性增大。在c～e时间段内，虽然外部轴向载荷线性增大，但是各滚子所受的法向接触力并不随外部轴向载荷的线性增大而线性增大。在c～d时间段内，各滚子所受的法向接触力保持不变，这是由于所施加的外部轴向载荷小于派生轴向力，滚子与内圈的相对位置没有发生任何改变，它们之间的接触力也保持不变。从d时刻开始，各个滚子承受的法向接触力开始明显近似线性增大，这是因为外部施加的轴向载荷大于派生轴向力，滚子与内外圈之间被挤压，导致法向接触力增大。在e时刻，各滚子所受的法向接触力达到最大值。

▲图5 滚子与内圈之间法向接触力变化曲线

各滚子所承受的径向与轴向接触力的变化规律与法向接触力在受载过程中的变化规律类似。

表1给出了轴承在c时刻承受80 000 N纯径向载荷和e时刻承受80 000 N径向载荷与60 000 N轴向载荷时，各滚子所承受的径向力和轴向力。由表1可知，径向载荷为80 000 N时，滚子径向方向的合力为79 988.7 N，相对径向载荷的误差为0.01%，轴向方向的合力为31 345.3 N，相对派生轴向力的误差为0.01%；径向载荷为80 000 N、轴向载荷为60 000 N时，滚子径向方向的合力为81 212.5 N，相对径向载荷的误差为1.16%，轴向方向的合力为57 087.3 N，相对轴向载荷的误差为4.85%。

图6为挡环与内圈端面之间法向接触力随外部载荷逐渐增大的变化曲线。由图6可以看出，a～c时间段内，挡环与内圈端面之间的法向接触力随径向载荷的线性增大而增大，产生的派生轴向力完全传递给了挡环；而在c～e时间段内，随着外部轴向载荷的线性增大，挡环与内圈端面之间的法向接触力线性减小，直至挡环与内圈端面逐渐分离，法向接触力为0。理论上，外部轴向载荷达到派生轴向力时，也就是在d时刻，挡环与内圈端面法向接触力接近于0。但是，派生轴向力的作用位置在轴承中心下方，造成内圈变形，导致在d时刻挡环与内圈端面之间仍有较小的法向接触力，随着外部轴向载荷的继续施加，内圈端面与挡环的分离程度继续变大，两者之间的法向接触力继续减小，直至法向接触力为0。

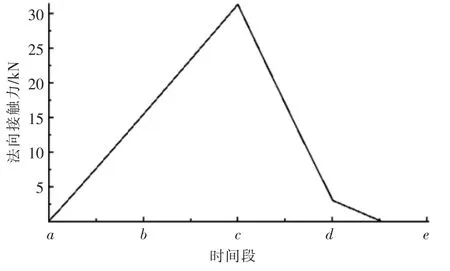
▲图6 挡环与内圈端面间法向接触力变化曲线

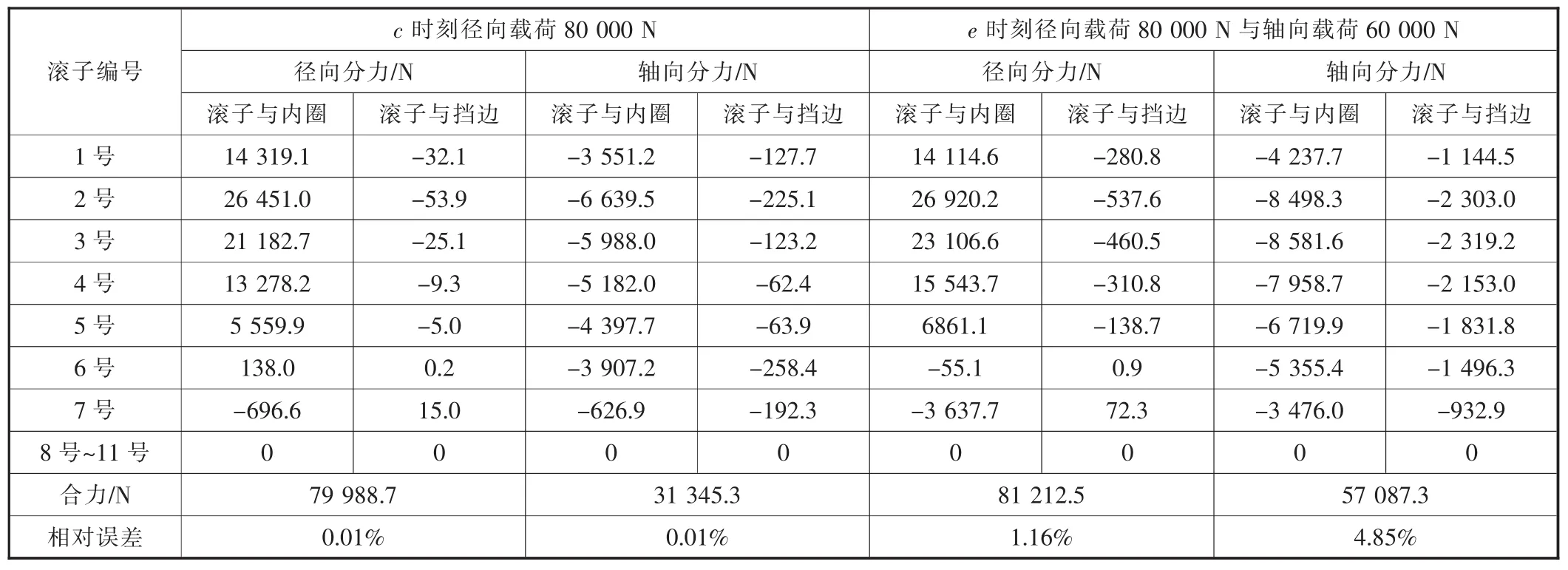
表1　滚子受力情况

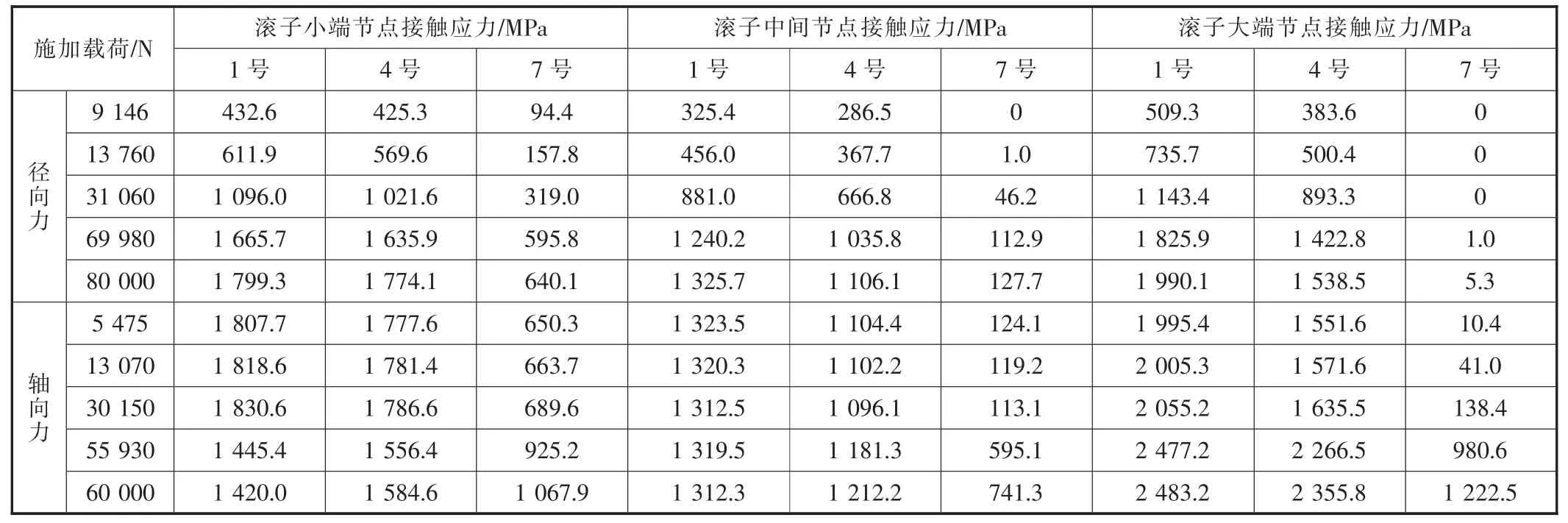
表2　节点接触应力

随着外部载荷的不断增大，每个滚子承受的接触力在不断增大，那么滚子的接触应力如何变化呢？由于8号～11号滚子在加载过程中，滚子与内圈的接触力一直为0，不承受任何载荷，因此选取轴承1号、4号、7号滚子与内圈接触的母线上小端、中间和大端各节点进行细致研究，表2给出了这些不同位置节点在不同受载时刻的接触应力。

由表2数据分析可知，随着径向载荷的逐渐增大，轴承内圈在径向向下移动，轴承下端的滚子主要承受径向载荷。由于边缘效应，轴承下端每个滚子两端的接触应力均比中间的大。随着径向载荷的增大，各节点的接触应力也在增大。轴承上端的7号滚子从小端开始接触，随着径向载荷的逐渐增大，接触位置逐渐向大端移动。随着轴向载荷的逐渐增大，在一定范围内轴承下端的滚子接触应力有所改善，1号滚子小端和中间法向的接触应力有所减小，4号滚子小端的接触应力也有所减小。7号滚子三处节点的接触应力随外部轴向载荷增大而增大。可见，轴向外部载荷的增大，在一定程度上改善了轴承下端滚子受力不均的情况。轴承各滚子中最大接触应力始终出现在1号滚子，且是在1号滚子的大端处。在c时刻，也就是径向载荷达到最大值时，1号滚子最大接触应力值为1 990.1 MPa。在e时刻，也就是轴向载荷达到最大值时，1号滚子最大接触应力值为2 483.2 MPa，此时的应力云图如图7所示。

3.2　外部轴向载荷与派生轴向力方向相同

施加载荷的大小和过程与上一节相同，只是施加外部轴向载荷的方向与派生轴向力方向相同。

滚子与内圈之间的法向接触力，在a～c时间段内与图5的变化规律一样，但是在c～e时间段内，无论施加的外部轴向载荷为多大，滚子与内圈之间的法向接触力及各方向的接触力都保持在c时刻的数值。与此相对应，接触应力在a～c时间段内与上一节变化规律一致，在c～e时间段内，每一节点的接触应力均保持不变。

▲图7 e时刻1号滚子最大接触应力云图

4　结束语

笔者采用有限元方法对圆锥滚子轴承进行仿真，研究先施加径向载荷、后施加轴向载荷对圆锥滚子轴承载荷分布与接触应力的影响。

随着径向载荷的逐渐增大，各滚子的法向接触力和接触应力均增大。各滚子的法向接触应力都存在边界应力集中现象，最大接触应力出现在1号滚子的大端处。

当外部轴向载荷与派生轴向力方向相反时，轴承所承受的轴向力为派生轴向力和外部轴向力两者中的较大者。外部轴向载荷小于派生轴向力时，随着外部轴向载荷的逐渐增大，滚子与内圈的法向接触力保持不变，而内圈端面与挡环间的法向接触力不断减小。外部轴向载荷大于派生轴向力时，随着外部轴向载荷的逐渐增大，滚子与内圈的法向接触力也逐渐增大，且各滚子与内圈的法向接触力之和等于外部轴向载荷。在径向载荷和轴向载荷的共同作用下，各滚子因所处的位置不同，接触应力的变化规律也不相同，1号滚子的接触应力始终随外部载荷的增大而增大，且1号滚子大端处的接触应力是轴承中的最大接触应力。

当外部轴向载荷与派生轴向力方向相同时，轴承所受的轴向力大小始终为派生轴向力。图5中c时刻后，无论外部轴向载荷多大，滚子与内圈的法向接触力和接触应力始终保持不变，施加的外部轴向载荷完全传递给了挡环。

［1］ 罗继伟.滚动轴承受力分析及其进展［J］.轴承，2001（9）：28-31.

［2］ 彭文生，黄华梁.机械设计教学指南［M］.北京:高等教育出版社，2003.

［3］ 马书尧.角接触滚动轴承轴向力分析的讲法［J］.河北工业大学成人教育学院学报，2003，18（3）:7-10.

［4］ 陈强，兰箭，华林.圆锥滚子轴承在径向力、轴向力和力矩载荷作用下的整体接触应力分析［J］.中国机械工程，2017，28（10）：1178-1182.

［5］ 杨霞，鄢闯，肖宏，等.利用轴承边界元法分析轴向力对四列圆锥轴承载荷的影响［J］.机械设计与研究，2014，30（2）：72-75， 79.

［6］ 魏延刚，王赫男，邵阳.圆柱滚子轴承载荷分布的三种计算方法比较［J］.机械制造，2016，54（7）:78-80，104.

［7］ 魏延刚，王发锋，李海涛，等.圆锥滚子轴承负荷分布及其动力学仿真［J］.大连交通大学学报，2014，35（S1）：60-63.

［8］ 魏延刚，董超.高速列车轴箱圆锥滚子轴承滚子的对数修形［J］.大连交通大学学报，2014，35（5）:34-37.

［9］ 魏延刚，王冰冰.径向载荷对预负荷滚子轴承径向承载性能的影响［J］.大连交通大学学报，2011，32（2）:33-37.

［10］石亦平，周玉蓉.ABAQUS有限元分析实例详解［M］.北京：机械工业出版社，2006.