颗粒参数对螺旋离心泵流场及过流部件磨损特性的影响

申正精，楚武利，董　玮

（1. 西北工业大学动力与能源学院，西安 710129；2. 兰州理工大学能源与动力工程学院，兰州 730050）

(1. School of Power and Energy, Northwestern Ploytechnical University, Xi’an 710129, China;2. School of Energy and Power Engineering, Lanzhou University of Technology, Lanzhou 730050, China)

0　引　言

螺旋离心泵作为一种具有特殊叶轮结构的两相流泵，其叶轮是螺旋推进作用和离心作用的有机结合，与普通离心泵相比，有高效区宽、无堵塞性能好、抗汽蚀性能优等特点[1-2]，常被用于化工、冶金和河道清淤等领域。离心泵过流部件磨损问题会导致机组效率下降明显、可靠性低、更换过流部件周期缩短，造成能源和设备的巨大浪费[3-5]。

减轻磨损的根本途径是研究内流场特性和关键过流部件的磨损分布，通过改变输送条件，从而建立颗粒参数与磨损的定性和定量关联[6]。近年来，国内外研究人员通过试验与数值模拟的方式对固液两相流离心泵的冲蚀磨损问题开展了大量的研究工作。Li等[7]通过采用粒子成像测速（particle image velocimetry，PIV）技术，研究了离心泵内的非定常流动特性。Shi等[8]对PIV系统进行了一定改进，并测量得出了两相流下离心泵内流场各相的相对速度分布。邵春雷等[9-10]分析了采用高速摄影（highspeed photography，HSP）测量离心泵流场不同位置处流动信息的误差，并提出了控制误差的方法。但由于螺旋离心泵特殊的叶轮结构，计算域内的流动及其复杂，上述方法所能提供的信息较为有限。李昳等[11-14]分析了不同固体颗粒粒径下离心泵过流部件壁面颗粒相的速度分布，建立了滑移速度与磨损的关联。陶艺等[15]以一台离心式工程塑料渣浆泵为对象，通过快速磨损试验对叶轮和背叶片表面的磨损情况进行了定性分析，得到了过流部件严重磨损区域分布。张自超等[16]基于改进的 Euler-Euler方法，得出考虑湍动尺度效应后得到的带状磨损区和偏磨区的计算结果更符合离心泵实际磨损情况，但未考虑当颗粒尺度增加时的受力情况，以进行综合分析[17]。

磨损理论方面，Tulsa大学冲蚀与腐蚀联合研究中心提出的E/CRC模型和Mclaury模型已初步形成了磨损模型和机理的体系，特别是Mclaury模型，主要被用来预测含沙水对材料表面的磨损[18-20]。此外，基于大量冲蚀试验得到的OKA模型已被证实不仅适用于高速流下的大尺寸颗粒，对低速流下的小颗粒也具有很好的预测结果[21-22]。然而，通过对比上述文献可以发现：虽然对离心泵过流部件磨损的定性关联基本明确，但在不同颗粒参数下对过流部件各区域磨损机理的分析缺乏论证，以获得更加精确的定量关联。而经过较好验证的数值计算方法结合适当的磨损模型，可以弥补试验手段的不足，并能相对完整地提供计算域内流场信息，从而得出过流部件磨损规律。

本文以螺旋离心泵为对象，对含沙水条件下其计算域内的固液两相流场进行求解，并将Mclaury和OKA磨损模型中的关联因子函数进行推导和比较，从而对影响过流部件磨损的环境因素、颗粒物性和靶材性质所包含的影响因子与磨损进行关联，颗粒与过流部件表面的碰撞反弹通过Tabakoff颗粒恢复系数公式进行计算。在数值计算与试验结果相吻合的前提下，最终选取颗粒粒径、颗粒体积分数和颗粒速度为影响因子，对螺旋离心泵输送不同含沙水条件下过流部件表面的磨损机理进行了参数关联性分析，研究结果对螺旋离心泵水力设计和结构设计的进一步优化有重要意义。

1　计算模型

1.1　物理模型

本文研究对象试验原型泵及叶轮结构如图 1所示，泵设计参数为：流量Q=165 m3/h，扬程H=32 m，额定转速n=1 480 r/min，效率η=62%，必需汽蚀余量NPSHr=2.5 m。叶轮和蜗壳几何尺寸如表1所示。

图1　试验原型泵及叶轮示意图Fig.1　Prototype pump for test and sketch of impeller

表1　叶轮和蜗壳几何尺寸Table 1　Geometric dimension of impeller and volute

1.2　数学模型

1.2.1颗粒运动模型

颗粒在流场中轨迹的改变主要由重力、附加质量力、绕流阻力、Saffman升力、Magnus升力和Basset力等主导，为讨论方便，这里只列出颗粒在x方向的受力方程[23-24]，y、z方向上的受力情况与x方向的受力类似，不再赘述。

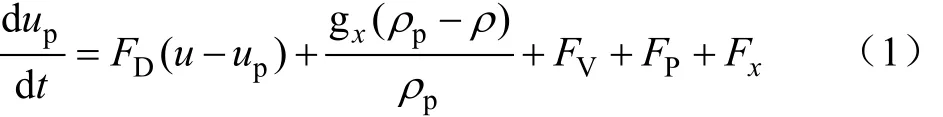
式中FD(u-up)为固相颗粒的单位质量曳力。

式中 u 为流体相速度，m/s；up为颗粒速度，m/s；μ 为流体动力黏度，N·s/m2；ρ为流体密度，kg/m3；ρp为颗粒密度，kg/m3；dp为颗粒直径，mm；gx为 x方向重力加速度，m/s2；Re为相对雷诺数；CD为曳力系数；FV为附加质量力，N；FP为压力梯度相关附加力，N；Fx为颗粒所受其他外力的合力，N；t为流动时间，s。

1.2.2颗粒恢复系数模型

为求解颗粒与过流壁面碰撞后的运动轨迹，需对颗粒碰撞后的反弹速度和方向进行计算。当颗粒冲击过流壁面时，动量的损失会导致反弹速度小于冲击速度，该作用通常采用恢复系数来描述，本文采用Tabakoff等碰撞试验总结所获得的恢复系数公式[25]

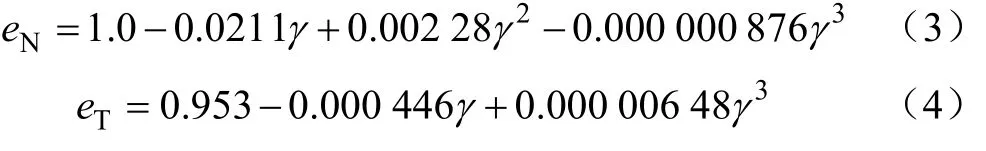
式中 eN为法向恢复系数；eT为切向恢复系数；γ为颗粒与壁面的冲击角度，(°)。

1.2.3磨损模型

1）Mclaury磨损模型

美国Tulsa大学 E/CRC磨损和磨蚀研究所Mclaury等提出了与颗粒速度、冲击角度、靶材硬度相关的磨损预测模型E，其表达式为[26]

式中E为表面磨损率，kg/(m2⋅s)；F为经验常数；V为颗粒速度，m/s；f(γ)为冲击角函数；γ为颗粒与壁面的冲击角度，(°)；Bh为壁面材料的布氏硬度，N/mm2；对于碳钢，指数 k= –0.59，A=1.997e–7，指数 n=1.73，冲击角函数可用如下分段多项式表达

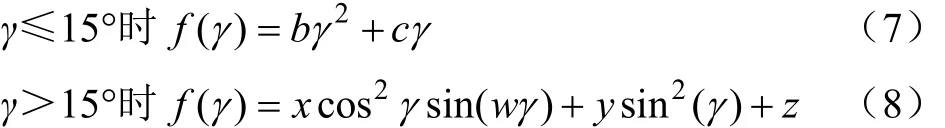
γ为颗粒与壁面的冲击角度，(°)；b、c、x、y、z、w均为常数，b= –13.3，c=7.85，x=1.09，w=1，y=0.125。

2）OKA磨损模型

相比较Mclaury模型，与之相互独立发展而来的OKA模型基于大量磨损试验，提出了一个包括颗粒速度和冲击角度、靶材硬度和颗粒尺寸等相关的方程E[21]

式中指数n1=0.8，指数n2=1.3；HV为维氏硬度，HV=1.8 GPa；E90为冲击角度为90°时的参考磨损率，可以表示为式中Vref为参考速度，Vref=104 m/s；d和dref分别为颗粒直径和参考直径，dref=326 μm；k1、k2和k3分别为硬度、速度和粒径指数，k1=–0.12，k2=2.3（HV）0.038，k3=0.19；K为经验常数。

2　数值计算方法及验证

2.1　网格划分及网格无关性验证

采用ANSYS ICEM软件对螺旋离心泵整机计算域进行网格划分，由于螺旋离心泵叶轮的结构复杂，选用对其适应性较强的四面体和三棱柱混合网格，如图2所示。在设计流量下，输送粒径为0.076 mm，颗粒体积分数为5%时，以隔舌处平均磨损率为指标进行网格无关性验证，如图3所示。最终确定各部分网格数为叶轮328 627，进口段27 509，叶顶与盖板间隙12 603，蜗壳100 980，网格数共为469 719。

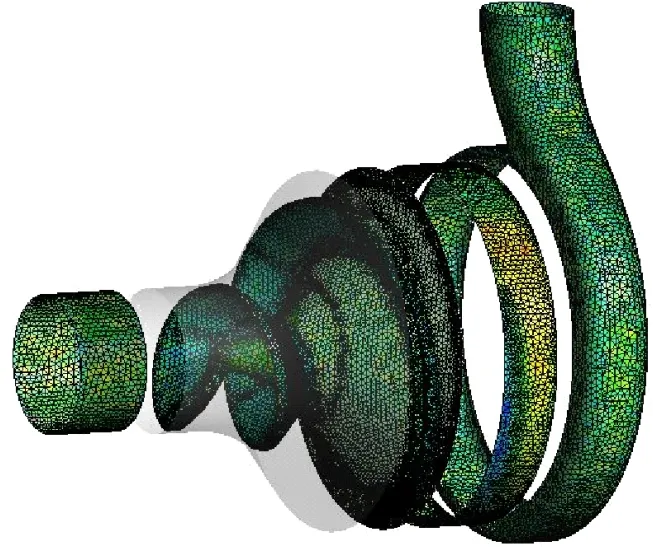
图2　螺旋离心泵三维模型网格Fig.2　Three-dimensional model mesh of screw centrifugal pump

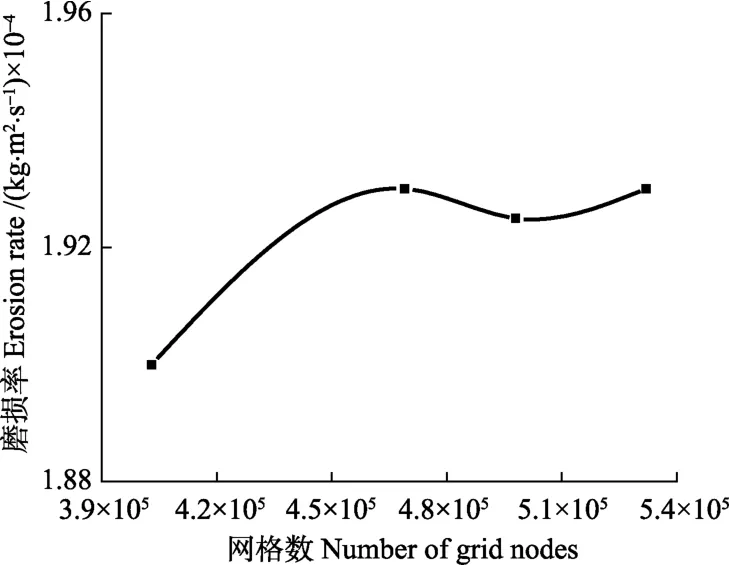
图3　网格无关性验证Fig.3　Grids independence test and verify

2.2　数值计算方法及边界条件

本文对螺旋离心泵内固液两相流内流体流动的求解在网格尺度上基于RNG k–ε 湍流模型进行[27]，对颗粒流动信息的求解采用离散相模型，并在 Fluent软件中分别引入Mclaury和OKA磨损模型进行对比分析，动静计算域交界面设置为Frozen rotor，并采用壁面无滑移函数，压力与速度的耦合采用 SIMPLE算法，并用二阶迎风格式来离散 N-S方程，设置计算收敛精度为 10–4，当泵出口总压趋于稳定时，判断达到收敛标准。

含沙水对水力机械过流部件表面磨损过程复杂，为对工程应用提供合理参考，本文对计算模型做如下简化假设：1）将含沙水中沙粒当做稀疏相处理，这样可认为各组颗粒运动相互独立，即忽略颗粒间的相互作用，同时沙粒不影响液相流动；2）本文所研究的颗粒为黏性、绝热，且自身无湍流扩散的光滑塑性球体，且并非亚观尺寸颗粒(dp≈1～10 μm)，在计算时忽略颗粒的自身旋转效应所引起的其他外力；3）不考虑空化与流体腐蚀对过流部件的冲蚀和腐蚀协同作用。

颗粒在泵进口面上以相同速度均匀入射，进、出口边界条件分别设置为逃逸边界条件，当颗粒与过流部件以一定速度碰撞时，根据其弹性恢复系数不同，会发生动量的变化，叶轮和蜗壳计算域内过流部件表面的边界条件均设置为碰撞边界条件。

2.3　数值方法的试验验证

为了验证数值计算方法的合理性，将数值计算结果与原型泵在清水工况下的性能试验结果进行对比，试验在甘肃省流体机械及系统重点实验室进行，试验方法参照GB/T 3216-2005回转动力泵水力性能验收试验相关规定。泵出口流量测量选用 EMFMHMD3000型电磁流量计，测量精度优于0.5%FS；转矩转速测量选取NJ1型转矩转速传感器，精度等级为0.2级；进出口压力测量选取ACC150PA型压力传感器，测量范围为0～4 MPa，精度等级为0.1级。通过测量进、出口压差、流量、主轴转速和转矩可获得扬程和效率值。

表2为泵性能数值计算值与试验值的相对误差分析。通过分析可知，扬程最大相对误差为3.82%，最小相对误差为 2.04%，平均误差为 2.95%；效率最大相对误差为3.21%，最小相对误差为1.54%，平均误差为2.3%，效率值的数值计算结果均高于试验值，主要原因为数值计算未考虑系统的机械损失和管路系统的沿程损失，计算结果整体上与试验结果较吻合，相对误差在可接受范围内。

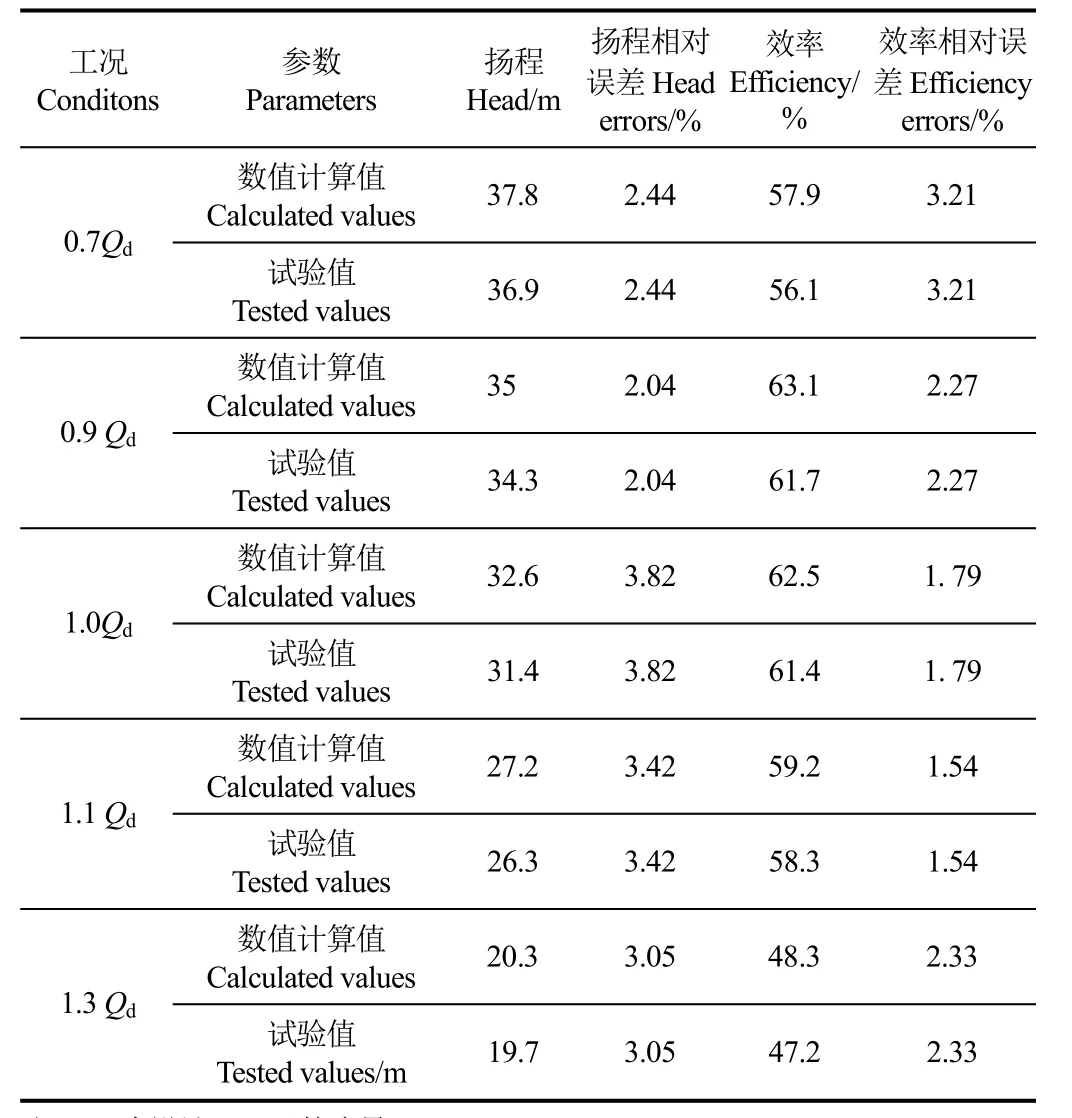
表2　泵性能计算值与试验值相对误差分析Table 2　Analysis of relative error between calculated and tested values of pump performance

3　影响因子的选择

过流壁面与颗粒的冲击、摩擦产生的磨损是与环境因素、颗粒物性和靶材性质等相关的复杂的函数，因而其磨损是多因素综合影响下的结果，单一的运用某一影响因子来评价磨损模型的优劣意义不大，考虑多因素联合作用，选择相对关键的影响因子与磨损进行定性和定量的关联是解决磨损问题的必要途径。

3.1　过流壁面材料属性与磨损的关联

分别定义上述 2种模型中与材料属性相关的函数Mclaury模型中，定义OKA模型中，颗粒速度和冲击角函数的关系中所涉及到的维氏硬度为小量，可以不予考虑，故定义

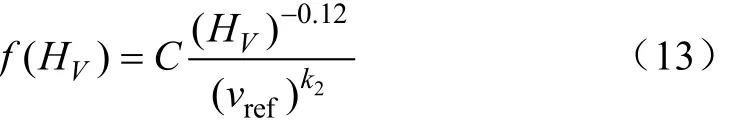
根据文献[28]所中给出的布氏硬度与维氏硬度之间的换算公式

当维氏硬度取值在1～9 GPa范围时，本文推导所得两种模型中材料相关函数曲线如图 4所示。可以看出两个函数具有几乎相同的变化趋势：材料硬度与磨损量呈负相关，即材料硬度越大，抗磨性能越好。

图4　过流壁面材料属性函数变化趋势Fig.4　Material properties function trend of flow passage components surface

3.2　颗粒冲击角函数与磨损的关联

从上述 2种磨损理论中冲击角函数的表达式可知，Mclaury模型中冲击角函数为分段多项式，而OKA模型中磨损率与冲击角呈指数关系。图 5展示了当过流壁面维氏硬度取1.8 GPa时，不同冲击角度下冲击角函数的变化趋势。可以看出，随着冲击角度的增大，2 种模型中的冲击角函数值先迅速增加，并在冲击角为40°附近达到最大，当冲击角大于40°后趋于平稳。虽表达式不同，但2种模型的冲击角函数走势不谋而合，展现出了相近的发展规律。

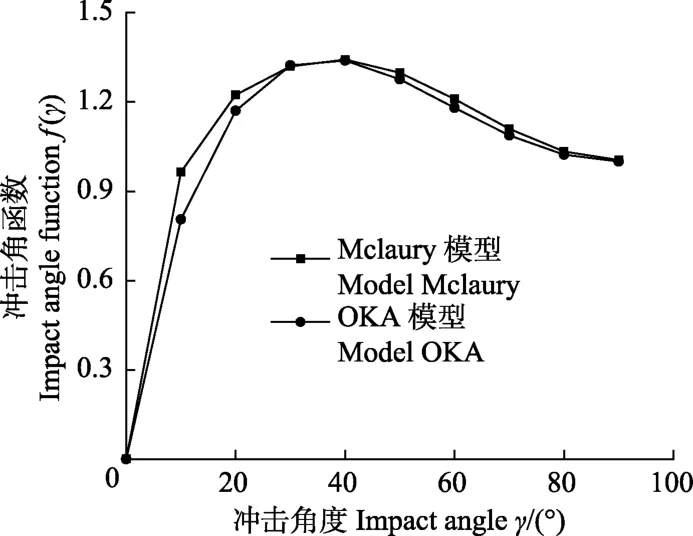
图5　冲击角函数变化趋势Fig.5　Variation trend of impact angle function

3.3　颗粒速度与磨损的关联

颗粒动能直接影响磨损量，两种模型中磨损量与颗粒速度的关系同样可定义为

式中vp为颗粒速度，m/s；n为经验常数，在Mclaury模型中，n=1.73；OKA模型中，n=2.35。可以看出，2种模型中颗粒冲击速度与磨损率均为指数关系，而且磨损率与速度呈正相关，只是指数的取值有所不同，无论是哪种模型，颗粒速度都是必不可少的关键性影响因子。

3.4　颗粒物性与磨损的关联

颗粒的硬度、形状、密度和粒径共同构成了其性能特点。对比Mclaury模型和OKA模型可知，在相同硬度和密度条件下，前者更多注重于颗粒形状对磨损的影响，用系数 Fs来表示颗粒形状：对于棱角颗粒，Fs=1，对于半球形颗粒，Fs=0.5；而对于球体颗粒，Fs=0.2[26]。而后者将粒径作为磨损严重与否的决定性因素[21]。本文选取研究的颗粒为光滑塑性球体，且颗粒密度均为2 650 kg/m3。

通过对以上 2种磨损模型中关联因子函数进行推导和分析，分别选取颗粒速度和粒径作为磨损的主导因素，本文试图达到以下 2个研究目标：其一，对计算域内颗粒参数改变所引发的过流部件表面磨损机理进行定性判别，并通过 2种磨损模型计算，以建立更加精确的颗粒参数与磨损的定量关联；其二，结合本文研究结果，为螺旋离心泵进一步优化水力设计，从而提高主机性能提供指导方向。

4　结果及分析

4.1　计算域内流场分析

图6为设计工况下，输送粒径为0.076 mm，颗粒体积分数为5%时，叶轮子午面上的流线及压力分布，从流线图可以看出，在叶轮旋转做功下，进入叶轮的流体流动方向逐步完成从轴向到径向的过渡，叶轮头部与流体的冲击角度较大，易诱发磨损。随着叶片包角增加，叶轮流道内沿流动方向压力升高，致使叶片工作面与背面产生压差，可以看出在叶轮流道子午面上，叶轮 420°包角附近的轮缘与盖板间隙处产生了显著的泄漏横向二次流，在主流压力驱动下，该二次流逐渐向流道中心发展，靠近处于叶轮240°包角附近的螺旋前段轮毂处。

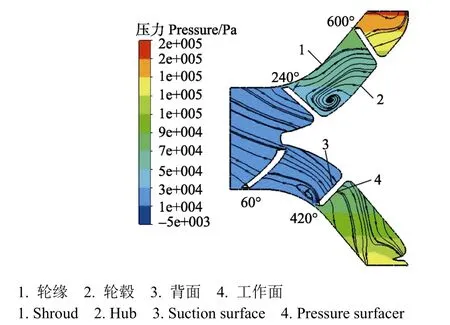
图6　叶轮子午面上压力分布与流线图Fig.6　Pressure and streamlines on meridian plane of impeller

为了更加清晰的分析流动结构沿叶轮流道轴向发展过程，在z轴方向分别选取3个截面，如图7所示，图8展示了每个截面的流线及压力分布情况。

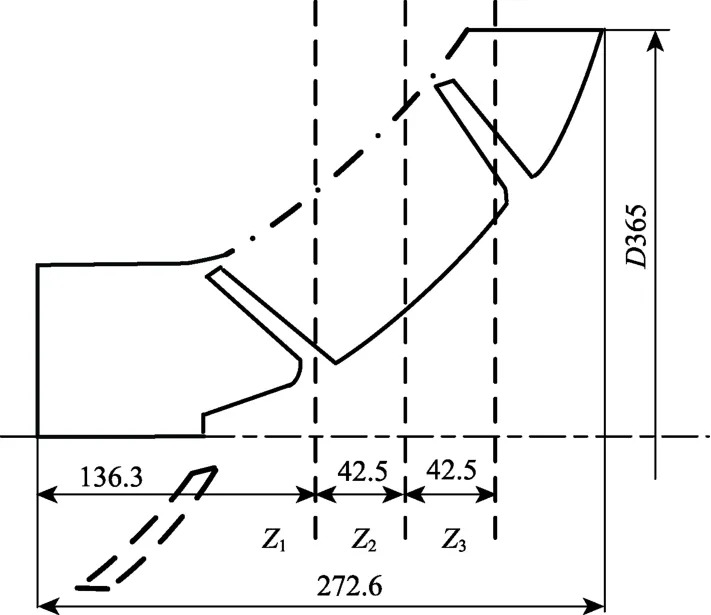
图7　轴向截面示意图Fig.7　Diagrammatic drawing of axial cross section

图8　轴向截面压力分布与流线图Fig.8　Pressure and streamlines on axial cross section

从图 8可以看出，叶轮通道内压力从叶轮轮毂到轮缘半径增大方向逐渐增加，根据欧拉方程可知，叶轮流道内的流体在叶轮旋转带动下实现能量提升，绝对速度V和牵连速度 U在叶轮出口处均得以增加。定义旋流比 ζ为叶轮通道内相同半径处的流体旋转速度 vθ与叶片牵连速度ωr之比[29]。显然，在叶轮旋转做功过程中ζ小于1，这使得流线方向与叶轮旋转方向 ω相反。处于叶轮螺旋前段的Z1平面，相对于进口面，该平面流道面积扩大，导致叶片对流体约束力变小，从而在靠近叶片工作面轮毂附近产生与叶轮角速度方向相反的轴向旋涡；螺旋离心泵叶轮螺旋段作为主要做功部件，具有类似于多级泵叶轮逐级加能的作用，在Z2平面，流道面积继续增加，但轴向旋涡产生的扩散效应不及叶片做功下流体所获得压力和速度的增加，进而使Z1平面内的旋涡发展受阻，涡核尺寸减小；位于叶轮半径最大处螺旋段末端的Z3平面，流动趋于规律。这是因为流体速度和压力在该处进一步得到提升，绝对速度在圆周方向上的分量达到最大，由于液相流动结构直接影响固相颗粒的运动轨迹，因此该区域内颗粒速度也会很大，容易导致磨损。

4.2　叶片表面磨损分布

图9为设计工况下，输送粒径为0.076 mm，颗粒体积分数为5%时，螺旋离心泵叶片表面的磨损分布。由图9a可以看出，叶片工作面磨损主要分布在靠近泵进口的叶片头部区域和螺旋段轮缘附近，这是因为当颗粒进入叶轮时，受惯性作用的影响，其绝对速度在圆周方向上的分量很小，从而几乎以原有速度方向与叶片工作面碰撞，这种多颗粒、高频次的冲击令叶片工作面头部磨损严重；其次，在叶轮旋转作用下，颗粒圆周速度和径向速度均得以增加，会沿轮缘聚集，造成磨损。然而，通过图9b发现，叶片背面的磨损区域与叶片工作面磨损区域差别显著，主要集中在叶轮最大半径处之后的叶轮离心段部分。由螺旋离心泵叶轮工作原理可知，叶轮离心段是将流体动能转换为静压能的部件，叶轮半径沿离心段至叶轮出口方向逐渐减小，进而使叶片对流体的约束力降低，导致部分流体脱离叶片工作面直接进入蜗壳，从而降低了颗粒与工作面的接触频率；另外，由于叶片工作面与背面的压差，经过隔舌后返流入叶轮离心段的部分颗粒会沿叶片出口背面再次进入叶轮域，接受叶片旋转做功，并沿叶片背面重新被甩出，致使该区域磨损严重。

图9　叶片表面磨损分布Fig.9　Erosion wear on blade surfaces

4.3　磨损模型的对比验证

为了验证本文数值计算所采用磨损模型的适用性，在Fluent中分别引入Mclaury和OKA 2种磨损预测模型，并在与文献[5]相同的输沙条件下对螺旋离心泵内部流动进行计算，其中，输送粒径为0.27 mm，固相体积分数为5%，沙粒密度为2 650 kg/m3。依照文献中的测试方案，从泵出口开始，沿蜗壳周向将其内壁划分为11个区域，从而得出蜗壳内壁各个截面平均磨损率，划分示意图如图10所示，计算结果与实测值对比如图11所示。

图10　蜗壳截面划分原理Fig.10　Cross sections of volute on angular basis

由图 11可知，蜗壳内壁磨损区域主要集中在隔舌（θ=20°）和θ=300°截面附近，采用2种模型计算得出的各截面磨损率与实测值最大相差1.35 kg/(m2⋅s)，但蜗壳各截面磨损发展趋势均与文献[5]中的实测结果较吻合。Mclaury模型计算值较总体上实测值偏大，平均相对误差达到了 13.3%，而 OKA模型与实测值平均相对误差为6.4%，与试验结果较为接近。数值计算与试验结果在定量上误差较大是因为固相颗粒在相对运动过程中对过流部件的冲击、摩擦后，金属表面润滑膜被破坏，加剧磨损，数值计算还不能模拟由于过流部件表面被破坏后所产生的剧烈磨损阶段。在综合考虑 2种磨损预测模型所考虑的因素后，本文选择OKA模型来定量分析计算域过流部件表面的磨损情况。

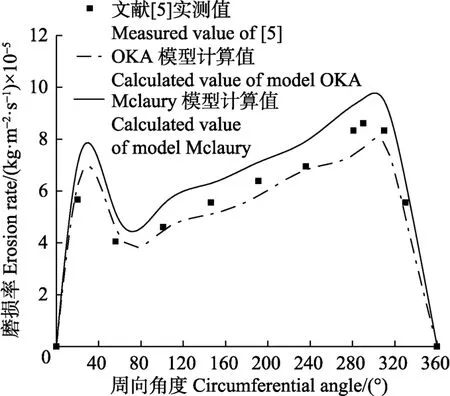
图11　蜗壳内壁磨损分布Fig.11　Erosion rate density on volute inner face

4.4　颗粒粒径对磨损的影响

以近年来黄河上游刘家峡水库变动回水区河段历年泥沙粒径级配为例，分别选取中值粒径在0.05至0.2 mm范围内的颗粒为研究对象，计算了不同粒径对计算域内过流部件平均磨损量的影响，由图12可知，颗粒尺寸从0.05增大到0.16 mm范围内，蜗壳内壁磨损量呈线性增加，颗粒粒径的增加对磨损起促进作用。由St数的定义[30]可知，颗粒尺寸增加使St数变大，弛豫时间增加，颗粒更易穿过尾涡和边界层后与过流壁面碰撞，加剧磨损。当中值粒径大于0.16 mm后，磨损量增长放缓，并趋于平稳，颗粒的“尺寸效应”抑制了磨损的发展：在相同颗粒体积分数下，颗粒尺寸增大会使单位时间内通过流道的颗粒数目减少，与过流部件表面碰撞的几率减小，从而磨损的概率也随之降低，磨损几乎不再增加。由此可知，研究颗粒粒径对过流部件磨损的影响，不能单一考虑粒径本身改变所产生的影响，而忽略单位体积内颗粒所占比率，即颗粒体积分数这一因素。

图12　不同粒径下蜗壳平均磨损变化Fig.12　Erosion rate density with different values of particle diameter

4.5　颗粒体积分数对磨损的影响

图13为设计流量下，粒径为0.05 mm，颗粒体积分数分别为3%、5%、6%和7%时蜗壳内壁的磨损率变化曲线。从蜗壳内壁磨损变化的整体趋势可以看出，磨损主要集中在隔舌附近和靠近出口的 θ=300°截面附近，这是因为在隔舌附近的颗粒流动比较紊乱，导致冲击磨损[11]；从 θ=101°～326°范围内，磨损呈增加趋势，这是因为在该区域内，蜗壳断面高度逐渐增大，过水断面面积增加，颗粒在离心力作用下，法向速度Vn变大，故而与蜗壳周壁的冲击角度增加，加剧磨损。颗粒体积分数由3%增加到6%范围内，磨损率随颗粒体积分数增加整体增大，而当颗粒体积分数由6%增加到7%范围内，隔舌处磨损率随颗粒体积分数增加而依旧增加，但在 θ=101°～326°的截面范围内，磨损率反而有所下降，这是因为隔舌处的磨损主要以冲击磨损为主，颗粒体积分数增加会导致颗粒与隔舌碰撞几率增加，但在隔舌之后的蜗壳周壁，固相颗粒体积分数的增加会使贴近于蜗壳近壁面的颗粒抑制其他颗粒的冲击作用，从而在一定程度上减缓了磨损。

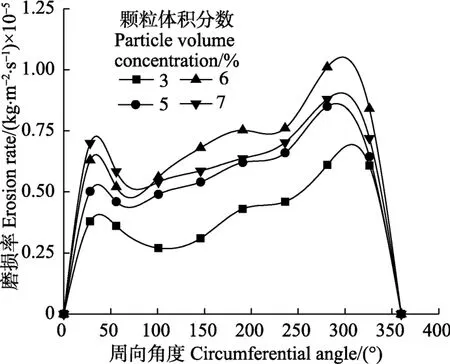
图13　不同颗粒体积分数下蜗壳内壁磨损率Fig.13　Erosion rate with different values of particle concentration

4.6　颗粒速度对磨损的影响

当颗粒粒径为0.05 mm，颗粒体积分数为7%时，在高效区附近流量内分别取流量为0.8 Qd、1.0 Qd和1.2 Qd3个工况点下对应的颗粒速度，得到蜗壳各截面平均磨损率如图14所示。可以看出，颗粒速度从1.96增加到3.15 m/s过程中，蜗壳内壁各截面平均磨损率整体增加，当颗粒速度从1.96提高到2.6 m/s时，蜗壳内壁最大磨损率增长了58%，当颗粒速度从2.6 提高到3.15 m/s时，蜗壳内壁最大磨损率增长了 50%，当颗粒速度为 3.15 m/s时周向281°截面处磨损率达到最高，达到 1.32×10–5kg/(m2⋅s)。蜗壳内壁各部位的磨损率变化趋势相近，磨损率与速度呈正相关，这是由于颗粒速度增大后St数相应增大，液相对固相的裹挟能力降低，颗粒与过流壁面碰撞后所受约束力变小，容易产生磨损。通过对比分析可知，与以上2个影响因子对磨损的影响规律不同，并不存在一个临界值，使得颗粒速度的提高对过流部件表面磨损起抑制作用，颗粒速度的变化对过流部件表面磨损率的影响较大。

图14　不同速度下蜗壳内壁磨损率Fig.14　Erosion rate with different values of particle velocity

通过以上分析可以看出，除了对关键过流部件表面严重磨损区域采取防护方法，根据本文的结果，可以在水力设计上对关键过流部件进行优化：结合性能试验，在对泵输送性能影响较小的情况下，适当减小叶片进口角，以降低固相颗粒与叶片头部的碰撞冲击角度；适当增加叶片背面出口附近厚度；蜗壳周壁应该设计为沿断面高度增加方向逐渐加厚的形式；若整体结构允许，隔舌可设计成可拆卸形式。

5　结　论

本文对螺旋离心泵输送不同含沙水条件下过流部件表面的磨损机理进行了参数关联性分析，得出以下结论：

1）固相颗粒对叶轮的磨损主要集中在叶片工作面头部、叶轮螺旋段轮缘、叶片背面离心段；对蜗壳内壁的磨损主要集中在隔舌和周向角度为300°截面附近。

2）颗粒粒径在0.05～0.16 mm范围内，粒径的增长对磨损起促进作用；而当粒径大于0.16 mm后，磨损量增长放缓，颗粒的“尺寸效应”抑制了磨损的发展。

3）颗粒粒径为0.05 mm，颗粒体积分数在3%～6%范围内，颗粒体积分数的增加会加剧磨损；而当颗粒体积分数从6%增加到7%时，蜗壳内壁各部分磨损情况有所不同：颗粒的冲击作用使得隔舌处磨损率随颗粒体积分数增加而增加，但在周向角度为 101°～326°的截面范围内，颗粒体积分数的增加会使存在于蜗壳近壁面的颗粒抑制其他颗粒的冲击作用，从而减缓磨损。

4）颗粒粒径为0.05 mm，颗粒速度从1.96增加到3.15 m/s过程中，蜗壳内壁各截面平均磨损率整体增加，并且在颗粒速度为3.15 m/s时，周向角度为281 °截面处的磨损率最高，可达1.32×10–5kg/(m2·s)，蜗壳内壁各部位的磨损率变化趋势相近，颗粒速度与磨损呈正相关，且对磨损的影响较大。

[参考文献]

[1] 张华，陈斌，王炳祺，等. 叶顶间隙大小对螺旋离心泵内部压力脉动的影响[J]. 农业工程学报，2017，33(1)：84－89.Zhang Hua, Chen Bin, Wang Bingqi, et al. Influence of tip clearance on internal pressure fluctuation of screw centrifugal pump[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(1): 84－89. (in Chinese with English abstract)

[2] Cheng X, Li R. Parameter equation study for screw centrifugal pump[J]. Procedia Engineering, 2012, 31: 914－921.

[3] Singh J, Kumar S, Mohapatra S K. Tribological analysis of WC-10Co-4Cr and Ni-20Cr2O3, coating on stainless steel 304[J]. Wear, 2017, 376 (4): 1105－1111.

[4] Tarodiya R, Gandhi B K. Hydraulic performance and erosive wear of centrifugal slurry pumps:A review[J]. Powder Technology, 2016, 305:27－38.

[5] 陈次昌. 两相流泵的理论与设计[M]. 天津：兵器工业出版社, 1994.

[6] 林建忠. 流-固两相拟序涡流及稳定性[M]. 北京：清华大学出版社, 2003.

[7] Li W, Zhou L, Shi W D, et al. PIV experiment of the unsteady flow field in mixed-flow pump under part loading condition[J]. Experimental Thermal & Fluid Science, 2017,83:191－199.

[8] Shi B, Wei J, Zhang Y. A novel experimental facility for measuring internal flow of Solid-liquid two-phase flow in a centrifugal pump by PIV[J]. International Journal of Multiphase Flow, 2017, 89: 266－276.

[9] 邵春雷，顾伯勤，周剑锋，等. 离心泵内部流动高速摄像测量及误差分析[J]. 农业工程学报，2015，31(24)：52－58.Shao Chunlei, Gu Boqin, Zhou Jianfeng, et al. Internal flow measurement in centrifugal pump by high speed photography and error analysis[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015,31(24): 52－58. (in Chinese with English abstract)

[10] Zhang J, Cai S, Li Y, et al. Visualization study of gas–liquid two-phase flow patterns inside a three-stage rotodynamic multiphase pump[J]. Experimental Thermal & Fluid Science,2016, 70: 125－138.

[11] 李昳，何伟强，朱祖超，等. 脱硫泵固液两相流动的数值模拟与磨损特性[J]. 排灌机械，2009，27(2)：124－128.Li Yi, He Weiqiang, Zhu Zuchao, et al. Numerical Simulation of solid-liquid two-phase flow and abrasion characteristics in desulfurization pump[J]. Drainage and Irrigation Machinery, 2009, 27(2): 124－128. (in Chinese with English abstract)

[12] 汪家琼，蒋万明，孔繁余，等. 固液两相流离心泵内部流场数值模拟与磨损特性[J]. 农业机械学报，2013，44(11)：53－60.Wang Jiaqiong, Jiang Wanming, Kong Fanyu, et al.Numerical simulation of solid-liquid two-phase turbulent flow and wear characteristics of centrifugal pump[J].Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(11): 53－60. (in Chinese with English abstract)

[13] 李昳. 离心泵内部固液两相流动数值模拟与磨损特性研究[D]. 杭州：浙江理工大学，2014.Li Yi. The Research on Numerical Simulation and Abrasion Property of Solid-liquid Two-phase-flow Centrifugal pump[D].Hangzhou: Zhejiang Sci-Tech University, 2014.

[14] Adnan Aslam Noon, Man-Hoe Kim. Erosion wear on centrifugal pump casing due to slurry flow[J]. Wear, 2016,364 (10): 103－111.

[15] 陶艺，袁寿其，张金凤，等. 渣浆泵叶轮磨损的数值模拟及试验[J]. 农业工程学报，2014，30(21)：63－69.Tao Yi, Yuan Shouqi, Zhang Jinfeng, et al. Numerical simulation and test on impeller wear of slurry pump[J].Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(21): 63－69. (in Chinese with English abstract)

[16] 张自超，王福军，陈鑫，等. 基于改进欧拉算法的双吸离心泵泥沙磨损特性研究[J]. 农业机械学报，2017，48(3)：124－133, 147.Zhang Zichao, Wang Fujun, Chen Xin, et al. Erosion characteristics of double suction centrifugal pump based on modified eulerian algorithm[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(3): 124－133,147. (in Chinese with English abstract)

[17] 李振中，魏进家，宇波. 稀疏气固两相槽道湍流中颗粒受力的理论和数值分析[J]. 中国科学院大学学报，2017，34(2)：146－152.Li Z Z, Wei J J, Yu B. Theoretical and numerical analyses of interphase forces in dilute particle-laden channel turbulence[J]. Journal of University of Chinese Academy of Sciences，2017, 34(2) : 146－152. (in Chinese with English abstract)

[18] McLaury B S, Shirazi S A An alternative method to API RP 14E for predicting solids erosion in multiphase flow[J].Journal of Energy Resources Technology, 2000, 122(3): 115－122.

[19] Parsi M, Najmi K, Najafifard F, et al. A comprehensive review of solid particle erosion modeling for oil and gas wells and pipelines applications[J]. Journal of Natural Gas Science & Engineering, 2014, 21: 850－873.

[20] Mansouri A, Arabnejad H, Shirazi S A, et al. A combined CFD/experimental methodology for erosion prediction[J].Wear, 2015, 332 (5): 1090－1097.

[21] Oka Yi, Yoshida T. Practical estimation of erosion damage caused by solid particle impact. Part 2. Mechanical properties of material directly associated with erosion damage[J]. Wear,2005, 258(1): 102－109.

[22] Oka Yi，Okamura K，Yoshida T. Impact-angle dependence and estimation of erosion damage to ceramic materials caused by solid particle impact[J]. Wear, 2009, 266(1): 129－135.

[23] 刘娟，许洪元. 离心泵内固体颗粒运动规律与磨损的数值模拟[J]. 农业机械学报，2008，39(6)：54－59.Liu Juan, Xu Hongyuan. Numerical simulation of erosion and particle motion trajectory in centrifugal pump[J].Transactions of the Chinese Society for Agricultural Machinery, 2008, 39(6): 54－59. (in Chinese with English abstract)

[24] Sun W, Zhong W, Zhang Y. LES-DPM simulation of turbulent gas-particle flow on opposed round jets[J]. Powder Technology, 2015, 270: 302－311.

[25] Wakeman T, Tabakoff W. Measured particle pebound characteristics useful for erosion prediction[C]// ASME 1982 International Gas Turbine Conference and Exhibit, 1982: 1－12.

[26] Jeremy K E, Brenton S M, Siamack A S. Modeling solid particle erosion in elbows and plugged tees[J]. Journal of Energy Resources Technology, 2001, 123(10): 277－284.

[27] 董玮，楚武利. 平衡孔直径对离心泵性能及平衡腔压力的影响[J]. 农业机械学报，2015，46(6)：73－77.Dong Wei, Chu Wuli. Influence of balance hole diameter on performance and balance chamber pressure of centrifugal pump[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(6): 73－77. (in Chinese with English abstract)

[28] Mahdavi M, Karimi S, Shirazi S A, et al. Parametric study of erosion under high concentrated slurry: Experimental and numerical analyses[C]// Proceedings of the ASME 2016 Fluids Engineering Division Summer Meeting, 2016: 1－10.

[29] Mortazavi F, Riasi A, Nourbakhsh S A. Numerical investigation of back vane design and its impact on pump performance[J]. Journal of Fluids Engineering, 2017, 139(10):1－9.

[30] 刘洪涛. 气固两相流中微细颗粒沉积与扩散特性的数值研究[D]. 重庆：重庆大学，2010.Liu Hongtao. Numerical Simulation of Micro-particle Deposition and Diffusion Characteristics in Gas-solid Two-phase Flow[D]. Chongqing：Chongqing University,2010.