有关等价变形在数学中的应用

四平市实验中学 吉林四平 136000

等价变形是数学解题方法中一种较为常见的类型，由于数学知识的复杂性，所以其变式较多，虽然，变式的多样化增加了解题的难度，但是在实际的解题过程中，我们依然可以通过等价变形来转换解题思路，降低解题难度，进而实现数学解题效率的提升[1]。

1 分式不等式与整式不等式的等价变形

在数学题目中，我们对于不等式的解题多需要进行不等式关系的等价转换，其中，利用等价变形的方法，将分式不等式转变为等式不等式，则能够使解题过程更加具有逻辑性。

解析：在该题目中，对于此类分式不等式的直接求解难度较大。我们在通常情况下需要变形，将其变为整式的形式，然后进行不等式的求解，这样解题过程将更加清晰。

由此可见，通过分式不等式向整式不等式的转化，整个解题的过程将变得更加简洁、清晰，但是，这里需要注意的是，在由分式向整式转化的过程中，我们需要注意分式中分母不为零的前提条件，否则将容易导致定义域的求解范围扩大[2-3]。

2 等价变形在三角函数中的应用

对于一些特殊的三角函数类型题目来说，其也可以用到等价变形的思想，尤其是对于一些存在着绝对值的三角函数而言。根据三角函数的特性进行解题，也可以使题目的难度明显降低。

由此，可以将函数Y进行以下变形：

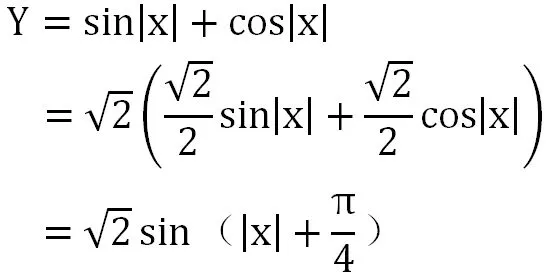
3 等价变形在证明题中的应用

证明题是数学题目中一种较为常见的题型，通过题目中已给出的相关信息，对所要求证的内容进行逻辑推理，进而得知证明对象是否成立。

解析：该题目所给出的条件较为单薄，看似无法为解题提供帮助，但是在这里，我们需要采用均值不等式与等价变形的方法来辅助求解。

根据均值不等式进行等价变形后可得：

4 结语

等价变形在数学解题中的应用范围较为广泛，并且，通过等价变形的学习，我们高中生能够了解到不同的变式形式，从而有助于提高我们的解题效率。为此，我们高中生不仅要在课堂上积极地掌握相关的数学知识，而且还需要在课下进行不断的练习，进而熟悉并适应各种题型，促进解题效率的提升。