关于函数解题中的数形结合思想分析

湖南冷水江市第一中学 湖南冷水江 417500

在高中学习数学的过程中，我们可以看到，函数始终贯彻于整个高中学习过程中，函数是数学学习的难点，在学习函数的过程中，我们对函数的理解有一定的困难，应当怎样才能更好地理解函数，是值得探讨的一个课题。在新课程背景下，数学思想方式的学习越来越受人们的重视，而数形结合思想是高中数学思想方法之一，在函数学习过程中有着不可缺少的作用，因此，此次研究对函数解题过程中的数形结合思想进行了分析和论述。

1 函数单调性解题中运用数形结合

分析：作为高中学生，我们在看到该题目的时候，应当进行审题，进而展开分析，通过审题，可以发现函数解析式里面包含了字母，所以函数在坐标系里面的详细位置无法固定，必须要通过画图来进行分析，看一看哪一种情况才可以充分满足题干的要求：

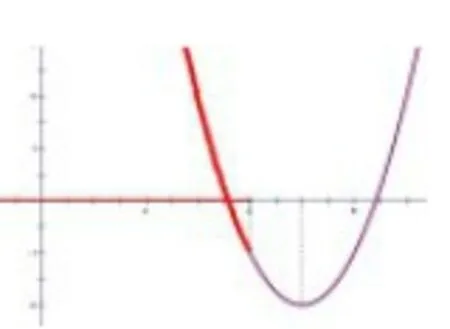
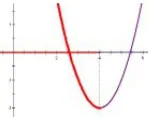
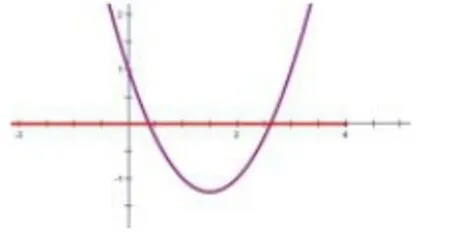
通过上述图像分析，我们可以了解到：假设要充分满足函数在定区间中是单调函数，只能够为后面两种情况，即函数图像对称轴不应当发生在所给区间以内，进而解题寻找到问题的突破口。给出来的函数对称轴方程就是：x=a-1，根据图像分析可以了解到，需要有a-1大于等于4，才会有a大于等于5。这种问题通常在二次函数里面，由于其单调性和对称轴的位置相关，因而一般画图分析可以更加直观地得到问题所需情况，进而在短时间内获取到最终结论。

2 函数值域解题中运用数形结合

在函数值域中国运用数形结合思想解题实际上就是把函数和图形有机结合在一起，进而采用图形的直观性计算出函数的值域。[1]

解析：当我们看到所计算函数是二次函数的时候，因为函数为非单调性的，因此，这不能够代入端点值来计算出值域，所以，必须要利用图像进行观察。见图所示。

利用图像可以了解到，这一函数的值域就是（-17/4，2]。

解答上述问题的对策：针对该种类型的数学问题是我们常见的出错点，因为作为高中生的我们习惯了直接代入端点值计算出其值域，所以对于给定区间中的二次函数值域问题，培养我们自身的数形结合思想是很有必要的。

3 函数最值解题中运用数形结合

利用数形结合解答函数最值，通常是把部分比较抽象的解析式给予几何意义，接着经过图形的属性与数量关系展开数和形的信息转变，将代数的问题等价性通过几何方式解答，让其求解变得更加容易。[2]

解析：我们可以通过观察已经给出来的函数的形式和结构，很容易发现这是两个点之间的距离之和，也就是可以将原函数转换成,原来的问题转变为“已经知道了P点（x,0）,计算它到两定点A（0,1），B(2,1)的距离之和最小值是多少”，继而结合图形，就可以将问题解答出来。

函数f(x)最小值就是|AP|+|PB|的最小值。作点A关于x轴的对称，就是点A,那么就可以得到|A`P|+|PB|。

如此就可以知道，当A`、P、B三点共线的时候，就存在最小值

解答该问题的对策：针对上述问题，原函数为二次根式，规定其最值若直接使用代数方式解题会更复杂，可是在这里，我们可以按照解析式将代数问题几何化，根据图形解答这一类数学问题，不仅有益于我们理解，同时解题步骤简单。

4 函数定义域解题中运用数形结合

函数三大要素中有一个要素就是定义域，计算函数的定义域是函数学习过程中的基本问题，面对计算函数的定义域问题，我们在看到题目以后，第一步就是将那些使函数有意义的条件一一列出来，等到计算出全部满足条件的解以后，使用对应的图形表达出来，进而逐次判断，如此才可以尽可能防止产生错误，得到准确的结论。

5 结语

总的说来，在高中数学学习过程中，函数是数学学习的重要内容，把数形结合思想结合到函数解题过程中，可以使复杂的代数问题变得更加简单，有益于建立简单的问题情境，同时还可以帮助我们灵活运用数学思想。因此，作为高中生的我们，只有掌握了准确的数学思想，才可以在数学学习过程中轻松应对函数方面的问题。