一种半径可控的参数化三维前缘钝化设计方法研究

柳 军，符 翔，王晓燕

(国防科技大学空天科学学院,长沙,410073)

0 引 言

高超声速飞行时，空气受到剧烈压缩而产生的气动加热使得飞行器面临巨大的热防护压力，因此高超声速飞行器在工程应用中必须要对存在的尖锐前缘进行钝化处理。在旋成体、升力体、翼身融合体等常见高超声速飞行器气动构型之中，乘波体具有升阻比大、设计过程简单等优点[1, 2]，是一种应用前景广阔的高超声速飞行器气动构型方案。但乘波体的设计原理决定了其外形必然带有尖锐前缘，这给热防护和加工制造带来一定困难，因此在设计时有必要对其前缘进行钝化处理。

现有的各种乘波体前缘钝化方法主要在材料增减和前缘钝化曲线类型两个方面存在差异：

a) 在材料增减方面，Stevens[3]提出了通过移除材料和增加材料两种途径进行前缘钝化的思路，如图 1所示，其中移除材料的方法被一些学者[4, 5]在研究中所采用。考虑到乘波体的前缘较薄，移除材料的方法可能对升力面的几何形状会产生较大影响，进而使得升阻比和容积减小。Tincher[6]在对增加材料的方法进行研究后指出：增加材料的方法对乘波体容积、升力面和流场结构的影响较小；

b) 在前缘钝化曲线类型上，部分研究[7, 8]中是采用圆弧来进行前缘钝化，其优点是设计过程简单，不足之处在于优化设计空间较小。如果乘波体上表面不是自由流面，采用圆弧钝化曲线将较难保证其与乘波体表面的光滑连接。Rodi[5]和Kontogiannis[9]分别提出了基于Bézier曲线和有理Bézier曲线的前缘钝化方法，前者针对前缘钝化设计参数开展了优化设计工作，后者则是研究了不同设计参数组合的影响。基于参数曲线的前缘钝化方法一定程度上拓展了钝化设计空间，且前缘钝化曲面与原飞行器的表面光滑连接。

图1 移除材料和增加材料两种前缘钝化思路对比

在高超声速飞行器的设计过程中，往往会根据飞行条件和热防护材料性能对前缘钝化提出相应的设计约束。本文根据实际需要，提出了一种半径可控的参数化三维前缘钝化设计方法，并利用CFD方法对钝化后的乘波体性能进行了评估。

1 前缘钝化设计方法

1.1 乘波体前缘点插值条件的获取

典型的乘波体构型由上、下表面和底面组成，其主要型线包括上、下表面的出口型线、激波出口型线以及前缘线。以吻切锥法[10]为例，其将给定的激波出口型线离散为多段小圆弧，每段均可以视作一小段圆锥激波，产生该段圆弧激波的圆锥称为吻切锥，经过该激波出口型线上的点和相应吻切锥轴线的平面称为吻切面。在各个吻切平面内，吻切锥顶点位置由激波角和该段激波圆弧的曲率中心确定，流场则是通过求解Taylor-Maccoll方程得到。对前缘点进行流线追踪可以得到相应的流线，而后将所有吻切平面内的流线组合成流面，即为乘波体的下表面。脊形吻切锥乘波体[11]是基于吻切锥乘波体所设计的改善了容积特性的乘波构型，其典型外形如图 2所示。

图2 脊形吻切锥乘波体示意图

由于前缘线为一条三维空间曲线，在进行前缘钝化时有必要将复杂的三维曲面设计问题简化为二维平面曲线设计问题，即先设计一系列的钝化前缘曲线，然后对其进行放样得到三维的钝化前缘曲面。就前缘钝化的方向而言，可以选择沿流向钝化和沿前缘法向钝化[9]。沿流向进行前缘钝化，则钝化前缘在各个横向站位上的钝化半径可直接确定，并且钝化前缘曲面与上下表面可实现流向上的光滑连接。此处采用增加材料的钝化思路，沿流向设计各个横向站位上前缘钝化曲线。乘波体未钝化时的前缘点记为P0，在对上表面沿法向抬升了高度h后，将上下表面端点分别记为P1和P0。相应地，前缘点处的插值条件包括P0点位置的切矢v0、曲率k0和P1点位置的切矢v1和曲率k1，如图3。

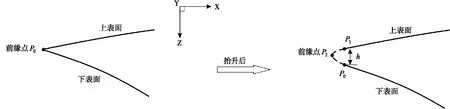
图3 上表面“抬升”前后的乘波体纵向截面示意图

对于一条xz平面上的曲线，如其解析表达式为z=f(x)，则其在点P(x,f(x))处的切矢和曲率可由下式得到

(1)

此处的向量叉乘定义为

a×b=(a1,a2)×(b1,b2)=a1b2-a2b1

(2)

考虑到乘波体，乃至一般飞行器的纵向截面曲线在多数情况下没有明确的表达式，此时可以通过对上下表面进行离散，然后对离散点进行差分获取端点处的1阶和2阶导矢，进而得到端点插值条件。

1.2 纵向截面钝化前缘线的构造方法

根据端点条件构造插值曲线的问题，可以看作插值于两个端点的GHI问题。该问题由de Boor[12]首次提出，其利用3次Bézier曲线插值于给定条件的平面上的两个点，从而解决了GHI问题。应用于GHI问题中的曲线类型有多种，其中Bézier曲线有着良好的凸包性和较简单的计算方法，在实际应用中有一定的优势。事实上，杨炯等[13]为解决压气机叶型前缘连续和前缘点曲率控制的问题，提出了一种可指定前缘点曲率的曲率连续前缘设计方法。该方法应用了两段3次Bézier曲线作为前缘曲线，实现了前缘与叶型的G2连续和前缘点的曲率控制。

3次Bézier曲线共需要4个控制点来进行曲线的设计，如图 4所示。

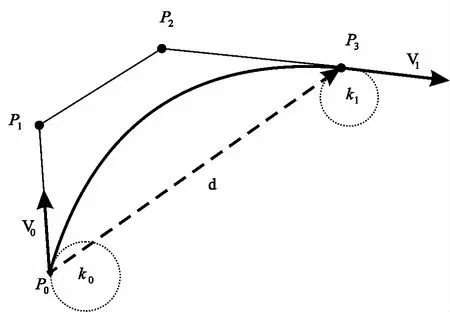
图4 三次Bézier曲线示意图

4个控制点间的关系可由下式表示

(3)

两个端点处的曲率为

(4)

由端点插值条件可以得到关于δ0和δ1的方程组

(5)

通过求解方程组(5)可以得到参数δ0和δ1的值，从而计算得到其余两个控制点的坐标，进而得到一条曲率连续的插值曲线。

利用前述的方法可以得到与乘波体上下表面光滑连接的钝化前缘曲线，但该曲线在前缘点处的钝化半径无法控制。此处利用2段3次Bézier曲线构造钝化前缘曲线，具体如图 5所示。在给定了前缘点的位置和前缘点钝化半径之后，便可由前述GHI算法分两次求解出钝化前缘曲线。

de Boor[12]讨论了方程组(5)的解的情况，指出该方程组可能有0至3个解。由于乘波体前缘线为三维空间曲线，各个横向站位处的端点插值条件不一，可能导致方程无解或者多解。如要将该方法应用于三维外形上，则对于方程组解的讨论将是主要障碍之一。此处对插值条件进行简化，即不要求钝化曲线与上下表面间的曲率连续，将钝化前缘曲线与上下表面连接处的曲率值设置为0。

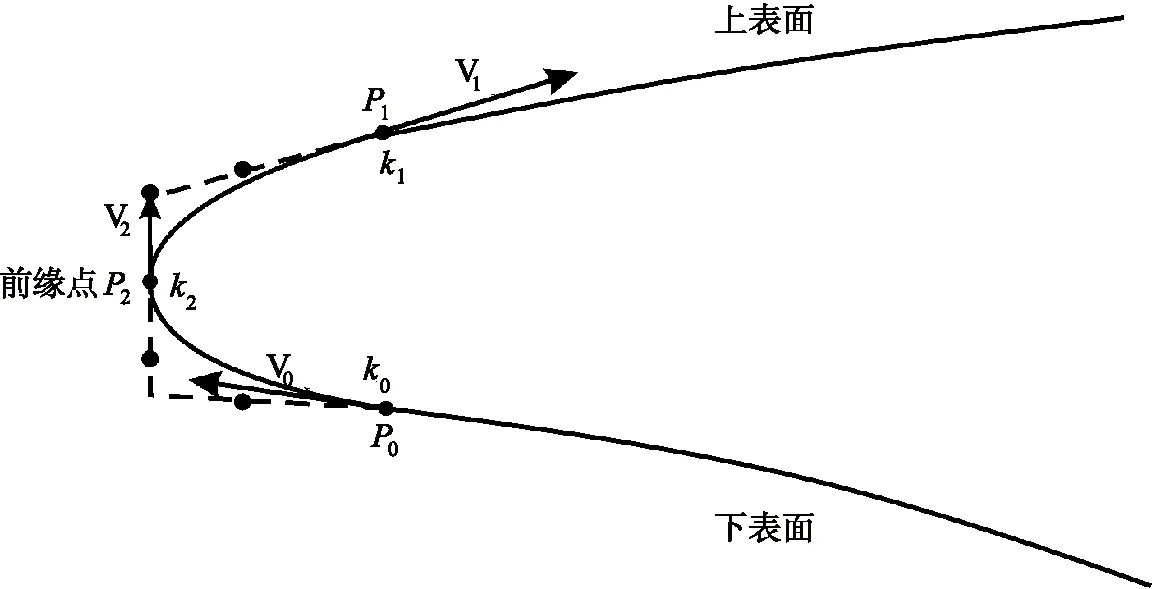
图5 利用2段3次Bézier曲线构造钝化前缘曲线示意图

方程组(5)可简化为

(6)

原方程组变为一个一元一次方程与一个二元二次方程的组合，不难看出，方程组(6)必然有且只有一个解。通过对插值条件的调整，以降低钝化前缘曲线与上下表面连接的光滑性为代价，简化了Bézier曲线的求解过程，有利于保持不同站位处前缘钝化曲线之间的连续性。

1.3 三维钝化前缘曲面的构造方法

在进行三维钝化前缘曲面的设计时，需要考虑不同横向站位处前缘点的钝化半径1/k2和位置P2以及上表面抬升距离h的设置。

乘波体纵向对称面处的驻点是热防护压力最大的部位，该处的前缘钝化半径应由热防护材料和飞行工况等条件确定。从减小阻力[14]或是最大限度利用热防护材料性能[9]的角度来看，可将其它站位处的前缘钝化半径适当减小。Rodi[5]提出了一种利用经验公式确定乘波体前缘钝化半径的方法，可由对称面处的钝化半径和当地前缘后掠角确定各横向站位处的钝化半径求出，如式(7)所示。

rswept=rsymmetry(cosλ)2.2

(7)

其中，rswept为非对称面处的前缘钝化半径，rsymmetry为对称面处的钝化半径，λ为当地前缘后掠角。

前缘点的位置P2和上表面抬升距离h的设置并无严格的解析表达式来可供参考，但应尽量满足以下两个要求：1)参数设置能使钝化前缘曲线能够成功生成，即δ0和δ1的值处于合适的范围内；2)在钝化前缘曲线上其它位置的曲率小于前缘点处的曲率。此处推荐将前缘点设置在上下表面延长线所构成夹角的角平分线上，如图6所示，其距P0点的水平距离l可由式(8)得出[9]。上表面抬升距离h的大小设置为当地前缘钝化半径的1～2倍即可。

l=r/cosλ

(8)

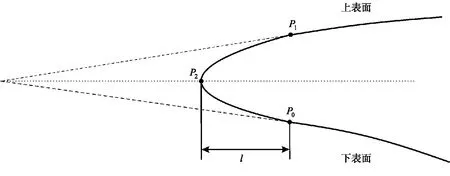
图6 新前缘点P2设置示意图

实际生成前缘钝化曲面时，较难保证所有生成的前缘钝化曲线均能满足前述两点要求，此时可以选取满足要求的曲线进行放样，从而得到所需的钝化前缘曲面。

2 设计实例

本文以脊形吻切锥乘波体为例进行前缘钝化设计。设计参数包括乘波体长度L、宽度W、设计马赫数Ma、激波角β以及上表面的设计参数而所用的设计型线为激波出口型线和上表面出口型线。为方便计算乘波体的前缘后掠角，设计下表面时给定的上表面出口型线为直线段、激波出口型线为2次曲线，具体如图 7所示。上表面纵向轮廓线采用二次曲线与直线段的结合，可以以较少参数来描述上表面纵向轮廓变化。

图7 激波出口型线示意图

部分设计参数的设置情况见表1。

表1 吻切锥乘波体部分设计参数

刘济民等[7]对采用不同钝化半径的乘波体性能进行了研究，发现当前缘钝化半径为20 mm时，乘波体具有好的综合性能。此处设置乘波体在纵向对称面处的钝化半径为20 mm，则根据式(7)得到的乘波体前缘钝化半径沿横向变化曲线如图8所示。考虑到当乘波体的后掠角较大时，对应的钝化半径较小，使得热防护系统的冗余度偏小，实际设计时可以使钝化半径稍大于理论值。

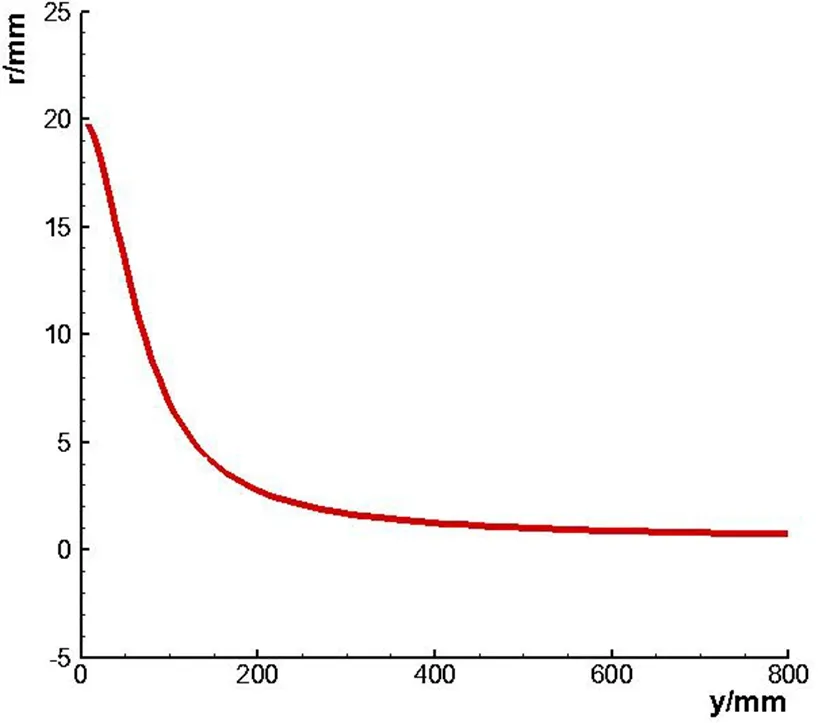
图8 最小前缘钝化半径沿横向变化示意图

最终得到的脊形吻切锥乘波体及其钝化效果如图9所示。

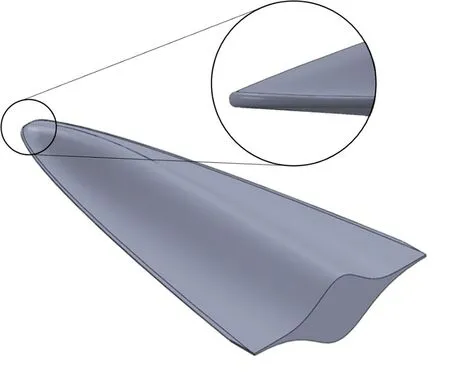
图9 脊形吻切锥乘波体等轴侧视图及头部钝化细节

3 气动性能分析

3.1 数值方法

由于乘波体为面对称外形，在只研究俯仰特性时可取一半流场进行数值模型，计算域包括了乘波体的底部。计算网格为非结构网格，为提高对边界层的预测精度，在壁面附近划分了棱柱网格以提高边界层的预测精度。流动控制方程为可压流的三维雷诺平均Navier-Stokes方程(RANS)，在计算中采用二阶迎风格式进行空间离散，时间项为隐格式。采用RNG κ-ε两方程湍流模型和增强壁面函数模拟湍流，壁面边界条件设置为绝热无滑移壁面。

3.2 计算结果分析与讨论

在马赫数Ma=8.0和高度H=31 km时，分析气动性能随攻角变化规律，如图10～图13所示。

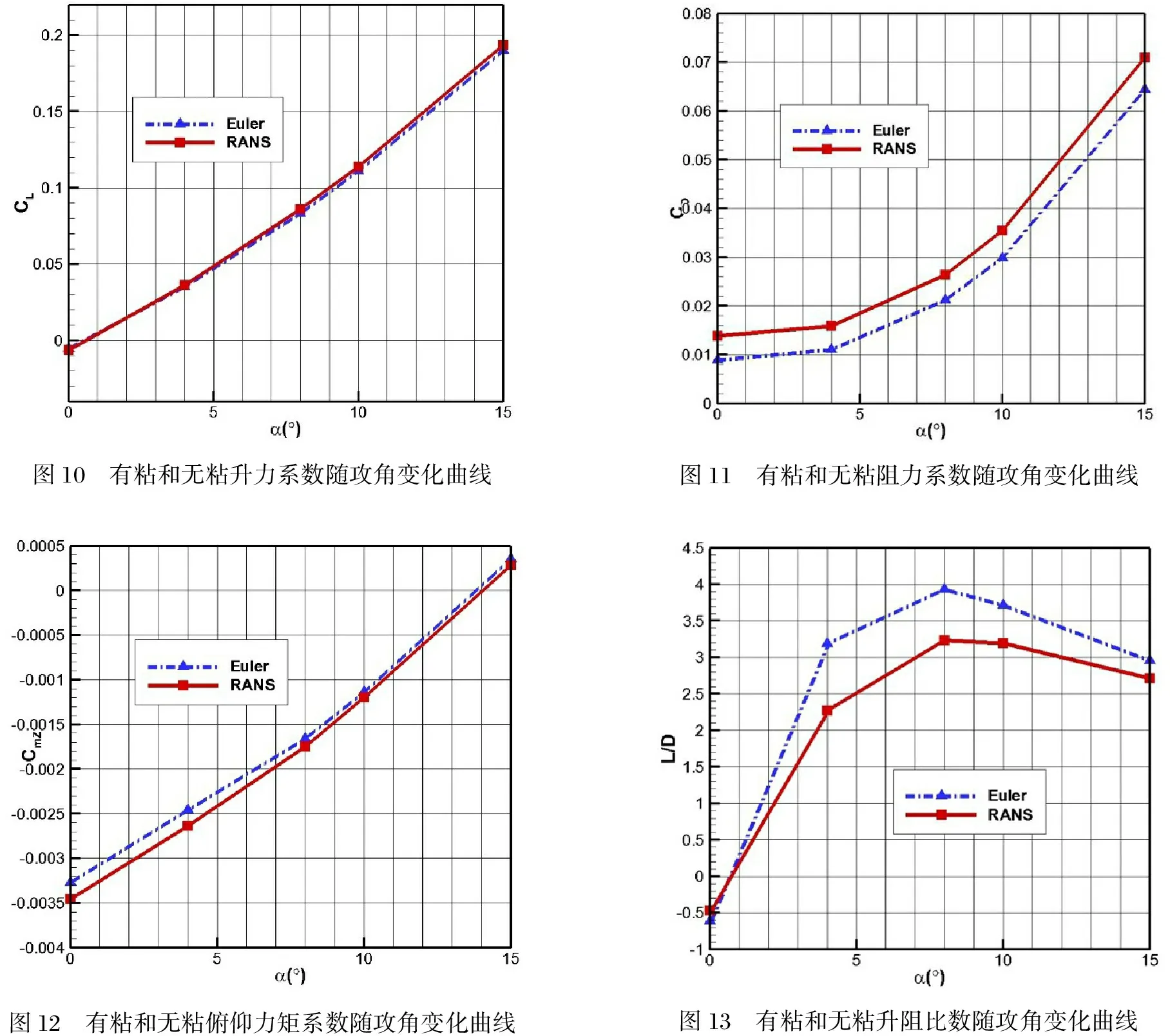
由以上各图可知，升力系数和俯仰力矩系数与攻角基本上呈线性关系，且值随着攻角的增大而增大。粘性对升力系数和俯仰力矩系数的影响不大，在飞行器设计初期可通过无粘计算快速获取升力特性和俯仰特性。由于高超声速流动具有强粘性的特点，乘波体阻力系数的有粘和无粘计算结果存在较大的差异。乘波体的最大升阻比出现在8°攻角，与一般研究[15]认为的最大升阻比出现在小攻角的结论不一致。可能的原因是本文采用了脊形的设计，上表面与一般乘波体所用的自由流面设计有较大区别，进而导致了升阻比和俯仰特性存在一定的差异。

4 结束语

本文针对乘波体的前缘钝化需求，提出了一种适用于高超声速飞行器的可控半径的参数化三维前缘钝化方法，并在此基础上利用CFD方法分析了钝化后乘波体的气动性能。不难看出，该方法主要有以下几个特点：

a) 乘波体前缘钝化过程实现了参数化，有利于程序实现和优化设计，减少了飞行器设计的工作量；

b) 钝化前缘曲面与乘波体表面光滑连接，可以避免飞行器表面不光滑对性能所带来的不利影响；

c) 前缘点以及前缘点处的钝化半径可以直接指定，使得气动外形设计与热防护系统设计可以实现有效衔接。

当然，本文中所提出的方法也存在一定的局限性：一是前缘钝化的部分设计参数的选取尚依赖于经验设计；二是前缘钝化曲面与飞行器表面连接的光滑程度需要进一步提高。虽然这两个问题并不影响该方法的实用价值，但也需要在今后继续研究以将该方法不断完善。

[1] 王卓. 乘波机外形设计 [J]. 北京航空航天大学学报, 1999, 25(02): 180-3.

[2] 许志, 唐硕, 闫晓东. 高超声速飞行器气动外形选择 [M]. 中国飞行力学学术年会. 2005.

[3] Stevens D R. Practical considerations in waverider applications [M]. AIAA Aircraft Design Systems Meeting. 1992.

[4] Naruhisa T, Mark L. Navier-Stokes computations of a viscous optimized waverider [M]. 30th Aerospace Sciences Meeting and Exhibit. 1992.

[5] Rodi P. Integration of Optimized Leading Edge Geometries Onto Waverider Configurations [M]. 53rd AIAA Aerospace Sciences Meeting. 2015.

[6] Tincher D J, Burnett D W. Hypersonic waverider test vehicle - A logical next step [J]. Journal of Spacecraft and Rockets, 1994, 31(3): 392-9.

[7] 刘济民, 侯志强, 宋贵宝, 等.前缘钝化对乘波体非设计点性能影响分析 [J]. 飞行力学, 2011, 29(1): 21-5.

[8] 陈小庆, 贺国宏, 江增荣, 等.乘波构型钝化方法分析及性能研究 [J]. 空气动力学学报, 2017, 35(1):108-114.

[9] Kontogiannis K, Cerminara A, Taylor N J, et al. Parametric Geometry Models for Hypersonic Aircraft Components: Blunt Leading Edges [M]. 20th AIAA International Space Planes and Hypersonic Systems and Technologies Conference. American Institute of Aeronautics and Astronautics. 2015.

[10] Sobieczky H, Dougherty F C, Jones K. Hypersonic Waverider Design from Given Shock Waves [M]. First International Hypersonic Waverider Symposium. 1990.

[11] 符翔, 柳军. 脊形吻切锥乘波体外形设计研究 [C].Proceedings of the 第十七届全国计算流体力学会议, 浙江，杭州, 2017.

[12] Boor C D, Höllig K, Sabin M. High accuracy geometric Hermite interpolation [J]. Computer Aided Geometric Design, 1987, 4(4): 269-78.

[13] 杨炯, 宁涛, 席平. 前缘点曲率可控的曲率连续前缘几何设计 [J]. 计算机辅助设计与图形学学报, 2016, 28(7): 1195-200.

[14] 刘建霞. 高超声速非一致边缘钝化乘波构型气动力/热基础问题研究 [D]; 国防科学技术大学, 2013.

[15] U.S. National Aeronauticics and Space Administration. Aerodynamic Characteristics of Two Waverider-Derived Hypersonic Cruise, NASA Technical Paper 3559 [R]. Hampton: NASA Langley Resarch Center, 1996.