高中数学数形结合解决问题方法研究

郑州市第四十七中学 河南郑州 450000

数形结合思想作为高中数学解题中较为常用的一种解题方法，能够将抽象的数学题目形象化，从而使题目的难度降低，简化解题步骤，提高解题效率。一般情况下，数形结合的解题方法能够适用于大多数的数学题目，如函数、方程、几何、数列等，在实际使用的过程中，根据不同的题目类型，可以选择与之相适应的数形结合解题方式，从而确保解题的准确度和效率[1]。

1 数形结合在三角函数解题中的应用

函数用来表示抽象的数量关系，因此，针对函数相关类型的题目，我们可以采取多元化的解题方式，其中就包括了利用数形结合的方法进行解题，通过坐标系中函数对应关系的转化，能够使题目中的变量关系更加清晰[2]。

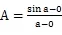
图1 函数在a、b两点上与原点连线示意图

2 数形结合在方程根的个数求解中的应用

在某些情况下，对于特殊方程根的个数的求解并不能够使用传统的解题方法，依然需要我们采用数形结合的方法解题，从而使此类题目的解题难度大大地降低，并能够实现解题效率的提升。

图2 关于与的示意图

3 数形结合在不等式中的应用

数形结合思想在数学中的应用较为广泛，除以上两种应用以外，不等式相关问题的求解也会与数形结合思想产生一定的联系。

解析：在分析该题目时，需要根据不等式的关系联立方程，即获得以下方程：，。

图3

4 结语

数形结合是解决数学题目的一种重要方法，然而，数形结合方法的熟练使用则需要依托我们高中生对数学基础知识的全面掌握，否则，在进行数形转化的过程中极易出现错误。同时，为了更好地应用数形结合方法，我们还需要加强对相关题目的训练，进而促进个人解题能力的提升。