高中数学学习中如何培养自身建模能力

胡伊淳

（巩义市第二高级中学 河南巩义 451200）

高中数学教学依旧采用传统应试教学模式，这种教学课堂不利于我们的数学学习。据我的观察分析，发现高中生数学学习的效率非常低下，很多学生课上、课下非常努力，但是数学成绩一直不理想。在这种身心具惫的学习中，大部分学生逐渐丧失了数学学习的兴趣与乐趣。我认为高中数学学习首先应具备数学建模意识，在日常学习中提升自己的数学建模能力。

一、重视课前问题学习，做好课堂学习反馈

高中数学教材中每一个章节都有课前导学问题，因此，在上课之前，我们应该自主学习导学问题，明确章节的重点内容，然后在数学练习中利用相关的数学模型解决问题。在课前导学中，我们会发现历史与生活中存在着很多的数学知识，当我们建立起数学学习的欲望，久而久之就会产生数学建模的欲求。例如，在高中数学函数教材中，导学问题中有对函数的物理解释：物体在进行匀速圆周运动的时候会进行周期性运动；我们家用的电流也在进行周期性变化；一年四季也在进行周期性变化[1]。那么，同学们如何利用数学知识解释周期性变化的[2]？此时，我们应发动自己的脑筋，结合课本内容提前预习周期函数内容，学习周期函数的理论与概念，通过教材中的案例归纳周期函数的特点等，提前做好课堂学习准备工作。

二、建立完善的数学模型

我们要善于利用已经掌握的数学知识，自行找到影响数学解题的主要依据。在解答数学问题时，如果我们发现问题中仅有一个影响因素，那么我们用一个简单的公式就可以进行表达。但是，高中数学题中大部分都有很多个未知数，解题过程中涉及多个未知公式，此时，就需要我们充分联系已经学过的数学知识，整理相关知识点给出数学模型。

例如，存在多个未知公式的数学题，首先，我们应该正确找出问题中的影响因数，根据题干内容和所学的数学知识确定各个未知数与已知数之间的关系，建立起具有关联的数学因素模型。在学习抛物线函数的时候，我们可以利用铅球运动轨迹进行数学模型构建，通过图1可以发现，铅球抛出的距离y=＝vsin·t－1/2 gt2＋h公式，x＝vcos·t[3]，这就是抛物线方程。在学习时，如果我们借助方程组求解，会让问题变得复杂。此时，我们可以把这两个方程有机整合。我们要探讨的问题就是铅球投掷的水平距离L，整个过程如：y=（g/2v2cos2）x2+ tan·x＋h。如果铅球掉落在地上，此时y＝0，这种情况下方程变为y＝（g/2v2cos2）x2+tan·x＋h＝0，此时再引入引入求根公式，可以轻松地求得x＝（v2sin2/2g±[（v2sin2/2g）2＋（2hv2cos2/g）]，在实际生活中y不可能是负值，因此，我们获得铅球的投掷距离模型：L＝（v2sin2/2g）＋[（v2sin2/2g）2＋（2hv2cos2/g）][4]。

当我们已经找到数学课本导学问题中的影响因素之后，此时，我们就可以将现实中的问题转化成数学函数，运用我们学过的数学知识，将未知的函数变为已知的数学公式，通过函数解决方式获得因素逐渐的关系。 这就是影响问题的函数公式模型。

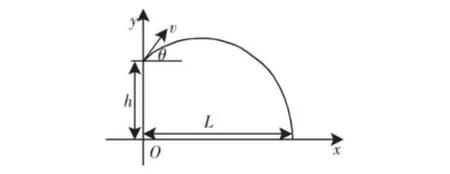
图1 铅球运动轨迹示意图

三、学会质疑，巧设数学问题

想象力大于知识，想象力重于知识，知识的力量是有限的，而想象力则是无限的，想象力可以是世界上所有的事物，想象力推动社会的进步的发展，是知识进化的本源。因此，在高中数学学习中，我们应具备丰富的想象力，实现数学创新教学，构建数学学习模型。多例高中数学学习实践案例证明，高中生的想象力强、新知识与新鲜事物的接受能力强，思维活跃，有很大的创新潜能，这些因素都为我们自身建模能力的培养与提升提供了先决条件。俗话说：“学启于思，思源于疑。[2]”心理学表示，思维意识的培养都是从问题开始的。只有心存疑点，心存问题，才会主动思考辨析，才会学会创新。学会质疑是高中生数学建模能力培养的有效途径之一。在日常学习中，我们应多多创设数学学习问题，正确提出质疑，自行解决问题。我们还应多多留意身边的事物与现象，善于观察生活中的数学问题，加强数学模型的应用意识与能力。同时，我们还应多浏览教材以外的数学书籍，多做数学练习题，在实际数学解题中培养我们的数学建模意识与能力。

结语

总之，数学建模是高中数学教学的一个热门话题，还可以培养我们的自主学习习惯，建立数学模型思想，提高高中学生的创造性思维和发散性思维，帮助学生认为在多个方面的问题，提高数学知识的实际应用能力。数学建模过程中引入数学教学可以使学生更加熟悉基本的教学内容，提高学生解决数学问题的能力。