初中数学利用有理数和无理数的性质解题探究
2018-04-13伍文玉
伍文玉
(湖南省永州市东安县端桥铺镇中学 湖南永州 425000)
在初中数学中,学生们首先接触到的就是实数,我们在学习的过程中,首先就要分清什么是有理数,什么是无理数。我们要分的清首先就要弄清楚有理数跟无理数的概念性质,初中生总是对概念理解不明确从而造成了这种题目错误百出。毕竟这些题是我们考试总能碰到的问题,虽然是基础性的问题但是学生们总出问题。笔者本文通过来讲解有理数与无理数的性质从而应用解题。
一、有理数跟循环小数的理解跟运算
有理数的概念我们要先弄清楚,整数跟分数我们都叫做有理数其中包含正整数、负整数、零、正分数、负分数。循环小数都可以转化为分数所以不管是有限循环小数还是无限循环小数都可以叫做有理数。例如1除以9得到的是0.1111111无限循环,也可称作九分之一,分数是有理数所以循环小数也是有理数。我们还要合理使用相反数、倒数和绝对值三项知识,因为弄清楚这些才方便我们计算,合理的解决问题。[1]
我们要熟练的运用有理数来计算问题。初中里的有理数运算跟我们小学里所学过的知识不同,我们不仅要算出数值的大小,还要弄清楚计算结果的符号。我们要合理的运用有理数来计算,做到熟练跟精确,使我们学习有理数跟无理数最重要的目的。他们是整个初中数学知识的基础。我们要向运用有理数的性质来进行解题还要学会有理数的运算法则和有理数的运算律。要理清楚有理数加、减、乘、除与乘方五种运算法则。有理数的加法法则是根据计算时同号,计算时出现异号还有出现零的时候怎么计算,当异号两数相加时我们需要特别注意别弄混了,很容易算错。这里就要求我们对绝对值得理解要深刻,搞不清楚绝对值这些完全不会的,所以不光是有理数的概念我们要学会,还要学会绝对值等利系列运算方法。
我们在进行有理数运算时我们要先乘除后加减,保证运算方法正确,然后注意正负号绝对值,这样我们才能保证自己解题的正确性。才能更好的运用到数学运算中。[2]
二、无理数跟无限不循环小数得概念跟运算
在初中数学涉及到无理数时,我们先推出的是计算根号2数值,然后发现他是无限不循环的小数,所有我们初步对无理数有了个认识。我们在学习无理数时,我们需要注意很多知识点,比如说无限不循环小数称为无理数的条件是要是小数,是无限不循环小数。有理数跟无理数是实数的组成部分使我们学习初中数学的重要基础,如果没有无理数就不能进行数学的计算,不能解决我们的日常生活问题。在进行无理数的学习时,我们必须先理解其基础概念,才能熟练地运用到计算中去。老师在引导学生们学习时,要激发学生的兴趣,调动学生们的思维性更好的理解无理数,从而在计算上不会出现问题。
我们可以给学生们讲典故激发起他们的学习兴趣。比如说2500多年前,古希腊有一位伟大的数学家毕达哥拉斯。在数学史上,毕达哥拉斯最厉害的地方就是发现了勾股定理。然后,希巴斯通过勾股定理,发现边长为1的正方形,其对角线长度不是一个有理数。然后毕达哥拉斯一直认为万物兼数,他说说的数就是整数。所以在希巴斯提出他的发现之后,毕达哥拉斯不敢相信,原来世界上真的有其他数的存在。毕达哥拉斯无法承受自己的理论将被推翻,所以他决定只要是关于其他数的问题,只能在学派内部讨论,不能传出去。但是希巴斯没有根据老师的指令守住这个秘密,把他的发现告诉了世人。这使毕达哥拉斯非常生气,所以他下令严惩希巴斯。希巴斯不得不逃出去,然后还是被人活捉,扔进了大海。但是,真理是不会消失的,毕氏学派抹杀真理是无理的举动。所以人们为了纪念希巴斯这位为真理而献身的人,就把不可通约的数取名为无理数,我们所知道的无理数就是这么来的。
例如把无理数在数轴上进行表示,进而帮助学生理解无理数,也能帮助学生进一步的理解数轴的含义。如下图在数轴上表示

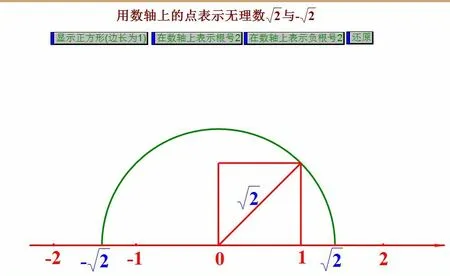
无理数的教学中,全新的知识点能激发学生的求知欲,还有很多学生因为遇到困难而放弃学习,我们首先就是要让他们理清楚概念这样在做题的时候才不会慌乱。首先要知道无理数这个概念有什么特点,然后再告诉他们在计算的时候可能遇到的问题,学生也需要把做题的时候遇到的问题及时向老师反馈。老师在教学的时候也要将无理数讲得简单易懂一点,这样学生才不会畏惧才能更好的理解这个东西。在学习做题的时候,我们需要及时发现学生在做题时遇到的问题,还有学生特别困惑的地方要向老师提出来,这样我们才能更好的在学习中做出反馈,更好的把这些教给学生。
三、概念性质的理解教学
在概念教学中,老师要清楚地了解到学生有没有理解这个概念跟性质。学生在学习一个新的知识概念的时候一般是根据自己的认知跟理解来学习的,但是一个新的概念有些时候跟以前接触过的其他东西不同,所以这时候就需要我们教师需要引导学生理解概念,应该依据学生概念学习的这种机制。学生理解后就能很好的运用进行计算,从而我们就正确的运用了性质进行计算。
我们对性质教学的完整过程,首先将性质引导给学生然后让学生记忆学习,只有这个样子我们才能更好教会学生理解性质从而运用到实际计算中。初中数学性质概念具有层次性的特点。我们需要将他们形成一个好的体系然后系统的认知。这样学生对抽象的概念性质的理解会提高,从而能更好的做题。
结语
在我们初中数学学习的过程中,在实数这一部分,对于有理数来说,无理数不能使用用分数来表达。我们需要注意的是,我们在数学计算题中经常会要求把结果通过四舍五入化为与准确值有差异的近似数。这样学生容易出现误会,错误认为分数可以化为无限不循环小数。数学教师应该多向学生强调,将某分数化为小数时,要求约值的意义并非等同于把分数化为小数。然后平时我们要加强反馈,告诉学生怎么去做题,总结做题的经验。只有我们先弄清楚有理数跟无理数的性质,才能将它们区分,在计算的时候合理的解决问题,绝对值与正负号也是我们必须掌握的,这是辅助我们做题计算必备的知识,我们只有掌握了有理数跟无理数的性质计算才能打好初中数学的基础,学好初中数学。
