变式训练在高中数学教学中的实践研究

王德江 施路成

（合肥师范学院 数学与统计学院 安徽合肥 230601）

长期以来，在数学教学中往往都是采用题海战术，通过反复训练同一种类型的题目来加深学生对学习内容的理解，以提高学生学习成绩。这样不仅令课堂教学效率低下，也使得学生思维容易固化，缺乏对问题的更深层次的思考。因为很多熟悉的知识，只要对问题稍加变化，学生就感觉无从下手。基于此，本文提出在教学过程中针对学生的特点创设合理的、有挑战性的变式训练，不仅能够激发学生的学习热情，提高学生的学习主动性，而且还能减小教师的教学压力，提高课堂教学质量与水平。[1]

一、初中数学教学中存在的问题

当前，在进行高中数学教学的过程中，大部分数学课堂依然沿用传统的教学模式，这种模式与当前新课改的要求存在一定的偏差，虽然学生成绩能得到相应的提高，但在教学中难以拓展学生的数学逻辑思维能力，学生未能真正掌握数学知识的内涵，更不用说体会到数学知识的魅力，这就使得部分学生更加厌恶数学，甚至产生了恐惧心理。另一方面，在教学过程中，教师采取的教学方式单一化。单一化的教学模式不能使教师对知识进行深入浅出地讲解，教师并不重视学生的实际需求，只是根据教学大纲照本宣科，这种方式使学生容易产生思维定势，限制学生思维的拓展，阻碍学生学习数学的学习积极性，导致学生在课堂中难以集中注意力，不利于学生未来的发展。[2]

二、变式训练的必要性

研究发现，大部分高考题都是由课本上的习题经过变换得到的，其解题步骤变化并不大。在备课过程中，教师应该善于发现并对经典的习题进行变式。通过变式，让学生从不同的角度发现并探究这一类习题的本质特征，从而彻底掌握解决该题方法的真正内涵。所谓数学变式训练，是指在数学教学过程中对概念、性质、定理、公式以及问题从不同角度、不同层次、不同情形、不同背景做出有效的变化，使其条件或形式发生变化，而本质特征却不变。在高中数学教学的过程中，变式训练具有以下优点：（1）利用变式教学能将一种问题演变成多种不同的题目，不仅能有效降低教师的教学强度，对学生的思维能力提升也能起到重要的作用。（2）将变式训练应用到数学教学中能有效提升学生的学习兴趣，使学生能运用多种不同的方式来解决数学问题。一道题目能找到多种形式来解决问题，这将对学生的兴趣提升起到重要的作用，同时对学生的学习积极性和学习自信心的提升起到重要作用。（3）学生能从原本单一的学习模式中得到解放，在变式题目中逐渐理解数学知识的关联性，并对解题的方法产生更加深刻的理解。因此，在日常教学中，教师应重视变式训练，并不断提升自我，不断改善自身的教学能力和教育理念。只有这样，在教学中教师才能更好地引导学生进行变式应用，提升学生的数学学习能力。[3]

三、变式训练的应用研究

[例1]设集合M={x|-2≤x≤5}，N={x|2-t＜x＜2t+1，t∈R}，若MIN=N，求实数t的取值范围.

解析：由MIN=N，得N⊆M.

若N=∅，有2t+1≤2-t，解得t≤

若N≠∅，由图1可得解得

综上可知，所求实数t的取值范围是t≤2.

当我们用上述方法解决了这个问题，学生或许有些明白解这种题目的“套路”，但如若在考试中稍加改变下题目条件：

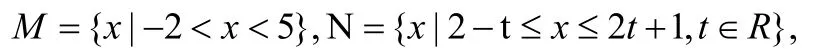
或M={x|-2≤x＜5}，N={x|2-t＜x≤2t+1，t∈R}，运算的结果可能就不大一样了，学生就顿时感到无从下手了，迷惑到底该如何使用“＜”和“≤”。这时教师在讲解习题时应采用变式训练的方式，对条件中的“＜”和“≤”进行变动，并且详细讲解端点处的包含关系，加深学生对端点处的理解，让学生明白什么情况下使用“＜”或“≤”。

[例2]已知函数f(x)=x2-4x-4，x∈[-1，1]，求函数f(x)的最小值.

解析：Qf(x)=x2-4x-4=(x-2)2-8

∴对称轴方程：直线x=2

∴函数f(x)在[-1，1]上单调递减，

∴f(x)min=f(1)=(1-2)2-8=-7

由例2我们知道函数f(x)开口向上，[-1，1]在对称轴x=2的左边，所以在x=1处取最小值。但学生可能只知道区间在对称轴的左侧是按照上述方法解答，却不清楚区间在对称轴的右侧，以及对称轴在所给区间内这两种情况该如何解答，这时就需要教师对上述问题进行变式，加深学生对最值问题这方面知识更深层次的理解。变式如下：[4]

变式一：已知函数f(x)=x2-4x-4，x∈[4，5]，求函数f(x)的最小值.

解析：Qf(x)=x2-4x-4=(x-2)2-8

∴对称轴方程：直线x=2

∴函数f(x)在[4，5]上单调递减，

∴f(x)min=f(4)=(4-2)2-8=-4

变式二：已知函数f(x)=x2-4x-4，x∈[0，4]，求函数f(x)的最小值.

解析：Qf(x)=x2-4x-4=(x-2)2-8

∴对称轴方程：直线x=2

∴函数f(x)的图像在[0，4]先下降后上升，

∴f(x)min=f(2)=(2-2)2-8=-8

像这样，再把这样两个变式展示给学生，学生就能更加深入地理解最值方面的问题。当然，同样可以把问题再次深化，将给定区间变为未知区间。

∴当对称轴在区间的左侧，即t＞2时，f(x)在区间[t，t+1]上是增加的

∴g(t)=f(t)=t2-4t-4;

当对称轴在区间内，当2∈[t，t+1]，即1≤t≤2时，

g(t)=f(2)=-8;

当对称轴在区间的右侧，即当t+1＜2，t＜1时，f(x)在区间[t，t+1]上是减少的，

∴g(t)=f(t+1)=t2-2t-7.

对称轴确定，区间不确定，需分对称轴在闭区间内、左侧、右侧三种情况求解，其中对称轴在闭区间左侧或右侧时可利用函数的单调性求解，在闭区间内时需比较两端点函数值的大小，若开口向上，则函数在对称轴处取最小值。[5]

当然，不是所有的高中数学问题都适用于变式训练，需要根据题目适时而定。变式可以将简单的问题层层递进，从而抓住问题的本质，使学生感觉到每一步骤都是合情合理地推导出来的；变式也可以把较难的问题进行梯度处理，先从稍简单的问题出发，再逐步加深接近原题，这样有助于帮助学生树立学习数学的自信，帮助学生克服一遇到难题就退缩的心理，从而提高学生学习数学的兴趣，更提高了高中数学课堂的教学效率。